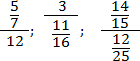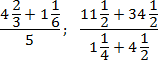Як вирішувати приклади із змішаними дробами. Дії з дробами

Калькулятор дробів від сайт дозволяє проводити всі основні математичні операції з дробами: додавання, віднімання, множення та поділ.

Ми намагалися зробити максимально зручний інтерфейс, тому для вказівки дробу Вам необхідно просто ввести у відповідне поле конструкцію виду 1/5 (для дробу "Одна п'ята") або 3 4/7 (Для дробу "Три цілих і чотири сьомих"). Зверніть увагу на необхідність вказівки пробілу між значеннями цілої та дробової частини.

Про калькулятор дробів онлайн

Пропонуємо вашій увазі калькулятор дробів онлайн від сайту. Цей пристрій буде корисним школярам, студентам, представникам технічних професій та всім тим, кому з тієї чи іншої причини доводиться при розрахунках стикатися з дробами. Наш калькулятор дозволяє миттєво виконувати основні математичні операції з дробовими та змішаними числами, з його допомогою ви зможете легко скласти, відняти, розділити та помножити дроби. Для розрахунків дробу вводяться у такому форматі: 3/9 (для дробу «три дев'ятих»), 5 4/5 (для дробу «п'ять цілих чотири п'ятих»). При роботі зі змішаними числами необхідно розділити пробілом цілу і дробову частину. При розрахунках із десятковими дробами їх необхідно попередньо перевести у прості і у потрібному форматі. Наприклад, десятковий дріб 3, 75 записуємо як 3 75/100, не забуваючи про пробіл між дробовим і цілою частиною.

Виконати рішення дробів онлайн калькуляторомдуже просто, але незайвим буде перед виконанням потрібних вам математичних дій згадати основні відомості про дроби та правила роботи з дробовими числами:

Звичайний дріб – це частина одиниці або кілька її частин. Знаменник дробу вказує, скільки рівних частин розділили одиницю, а чисельник – скільки таких рівних частин було взято.

З двох дробів з рівними знаменниками більшим є той, у якого чисельник більший.

З двох дробів з рівними чисельниками більшим є той, у якого знаменник менший.

Для порівняння дробів, що мають різні чисельники та знаменники, необхідно привести порівнювані числа до спільного знаменника.

У правильного дробузнаменник більший за чисельник.

У неправильного дробу чисельник більший за знаменник. З такого дробу можна виділити цілу частину.

Якщо чисельник дробу ділиться на знаменник, то дріб дорівнює числу, приватному від розподілу.

У неправильного дробу чисельник ділиться на знаменник із залишком і результат є змішаним числом.

Змішане число можна перетворити на звичайний дріб. Для цього цілу частину множать на знаменник, до отриманого числа додають чисельник. Результат записують у чисельник звичайного дробу, а знаменник залишають тим самим.

Наш калькулятор дробів онлайн може бути розміщений на вашому сайті. Для цього достатньо отримати спеціальний код.

Ця стаття є спільним поглядом на дії з дробами. Тут ми сформулюємо та обґрунтуємо правила складання, віднімання, множення, поділу та зведення в ступінь дробів загального виду A/B , де A та B деякі числа, числові вирази або вирази зі змінними. Зазвичай матеріал забезпечуватимемо пояснювальними прикладами з детальними описами рішень.

Навігація на сторінці.

Правила виконання дій із числовими дробами загального виду

Давайте домовимося під числовими дробами загального виду розуміти дроби, у яких чисельник та/або знаменник можуть бути представлені не тільки натуральними числами, але й іншими числами чи числовими виразами. Для наочності наведемо кілька прикладів таких дробів: .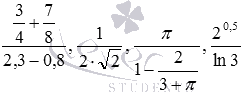

Нам відомі правила, за якими виконуються. За цими правилами можна виконувати дії з дробами загального вигляду:

Обґрунтування правил

Для обґрунтування справедливості правил виконання дій із числовими дробами загального виду можна відштовхуватися від наступних моментів:

дробова риса - це насправді знак розподілу,
розподіл на деяке відмінне від нуля число можна розглядати як множення на число, зворотне дільнику (цим одразу пояснюється правило розподілу дробів),
властивостей дій із дійсними числами,
та його узагальненому розумінні

Вони дозволяють провести наступні перетворення, що обґрунтовують правила додавання, віднімання дробів з однаковими та різними знаменниками, а також правило множення дробів: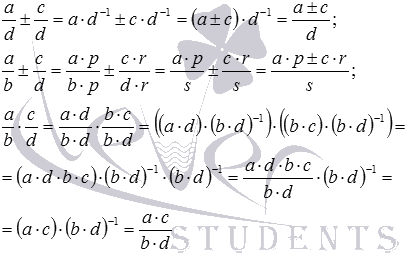

Приклади

Наведемо приклади виконання дії з дробами загального виду за розученими у попередньому пункті правилами. Відразу скажемо, що після проведення дій з дробами отриманий дріб вимагає спрощення, причому процес спрощення дробу часто складніше, ніж виконання попередніх дій. Ми не будемо докладно зупинятися на спрощенні дробів (відповідні перетворення розібрані в статті перетворення дробів), щоб не відволікатися від цікавої для нас теми.

Почнемо з прикладів складання та віднімання числових дробів з однаковими знаменниками. Для початку складемо дроби та . Вочевидь знаменники рівні. Згідно з відповідним правилом записуємо дріб, чисельник якого дорівнює сумічисельників вихідних дробів, а знаменник залишаємо тим самим, маємо . Додавання виконано, залишається спростити отриманий дріб: . Отже, .

Можна було рішення вести по-іншому: спочатку здійснити перехід до звичайних дробів, після чого провести додавання. За такого підходу маємо .

Тепер віднімемо з дробу дріб 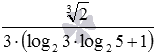. Знаменники дробів рівні, тому діємо за правилом віднімання дробів з однаковими знаменниками: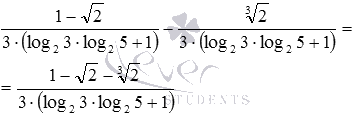

Переходимо до прикладів складання та віднімання дробів з різними знаменниками. Тут головна складність полягає у приведенні дробів до спільного знаменника. Для дробів загального вигляду це досить велика тема, її розберемо детально в окремій статті приведення дробів до спільного знаменника. Зараз же обмежимося парою загальних рекомендацій, оскільки даний моментнас більше цікавить техніка виконання дій із дробами.

Взагалі, процес схожий на приведення до загального знаменника звичайних дробів. Тобто, знаменники представляються у вигляді творів, далі беруться всі множники зі знаменника першого дробу і до них додаються множники, що відсутні, зі знаменника другого дробу.

Коли знаменники дробів, що складаються або віднімаються, не мають спільних множників, як загального знаменника логічно взяти їх твір. Наведемо приклад.

Допустимо, нам потрібно виконати додавання дробів і 1/2 . Тут як спільний знаменник логічно взяти твір знаменників вихідних дробів, тобто . У цьому випадку додатковим множником першого дробу буде 2 . Після множення на нього чисельника і знаменника дріб набуде вигляду. А для другого дробу додатковим множником є вираз. З його допомогою дріб 1/2 наводиться до вигляду. Залишається скласти отримані дроби з однаковими знаменниками. Ось короткий запис всього рішення: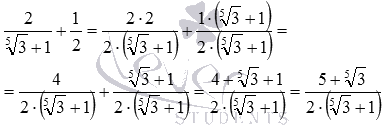

Що стосується дробів загального виду не йдеться про найменшому загальному знаменнику, якого зазвичай наводяться прості дроби. Хоча в цьому питанні все ж таки бажано прагнути деякого мінімалізму. Цим ми хочемо сказати, що не варто як спільний знаменник відразу брати твір знаменників вихідних дробів. Наприклад, зовсім не обов'язково брати спільним знаменникомдробів та твір 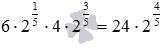. Тут як спільний знаменник можна взяти.

Переходимо на приклади множення дробів загального виду. Помножимо дроби та . Правило виконання цієї дії нам наказує записати дріб, чисельник якого є добуток чисельників вихідних дробів, а знаменник – добуток знаменників. Маємо 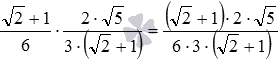. Тут, як і в багатьох інших випадках при множенні дробів, можна скоротити дріб: .

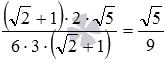Правило розподілу дробів дозволяє від розподілу переходити до множення на зворотний дріб. Тут слід пам'ятати, що для того, щоб отримати дріб, зворотний даному, потрібно переставити місцями чисельник і знаменник даного дробу. Ось приклад переходу від розподілу числових дробів загального вигляду до множення: 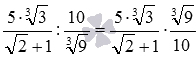. Залишається виконати множення та спростити отриманий в результаті дріб (при необхідності дивіться перетворення ірраціональних виразів):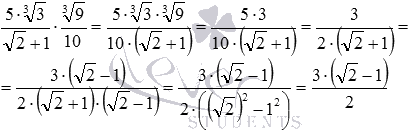

Завершуючи інформацію цього пункту, нагадаємо, що будь-яке число чи числове вираз можна подати у вигляді дробу зі знаменником 1 , тому, додавання, віднімання, множення та розподіл числа і дробу можна розглядати як виконання відповідної дії з дробами, одна з яких має одиницю у знаменнику . Наприклад, замінивши у виразі 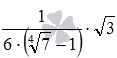корінь із трьох дробом, ми від множення дробу на число перейдемо до множення двох дробів: .

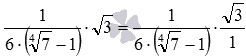Виконання дій із дробами, що містять змінні

Правила з першої частини цієї статті застосовуються і для виконання дій з дробами, які містять змінні. Обгрунтуємо перше їх – правило складання і віднімання дробів з однаковими знаменниками, інші доводяться абсолютно аналогічно.

Доведемо, що для будь-яких виразів A, C і D (D тотожно не дорівнює нулю) має місце рівність з його області допустимих значень змінних.

Візьмемо певний набір змінних із ОДЗ. Нехай при цих значеннях змінних вирази A, C і D приймають значення a0, c0 і d0. Тоді підстановка значень змінних з обраного набору у вираз перетворює його на суму (різницю) числових дробів з однаковими знаменниками виду, яка за правилом складання (віднімання) числових дробів з однаковими знаменниками дорівнює . Але підстановка значень змінних з вибраного набору у вираз перетворює його на той самий дріб. Це означає, що для вибраного набору значень змінних ОДЗ значення виразів і рівні. Зрозуміло, що значення зазначених виразів будуть рівними і для будь-якого іншого набору значень змінних з ОДЗ, а це означає, що вирази і тотожно рівні, тобто справедливість, що доводить рівність. .

Приклади складання та віднімання дробів із змінними

Коли знаменники дробів, що складаються або віднімаються, однакові, то все досить просто - складаються або віднімаються чисельники, а знаменник залишається колишнім. Відомо, що отриманий після цього дріб при необхідності і можливості спрощується.

Зауважимо, що іноді знаменники дробів відрізняються лише з першого погляду, але за фактом є тотожно рівними виразами, як, наприклад, 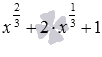і , або . А іноді досить спростити вихідні дроби, щоб «проявилися» їх однакові знаменники.

приклад.

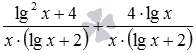, б) , в) .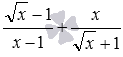

Рішення.

а) Нам потрібно виконати віднімання дробів з однаковими знаменниками. Згідно з відповідним правилом знаменник залишаємо колишнім і віднімаємо чисельники, маємо 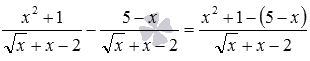. Дія проведена. Але ще можна розкрити дужки в чисельнику і навести подібні доданки: .

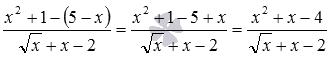б) Очевидно, знаменники дробів, що складаються, однакові. Тому, складаємо чисельники, а знаменник залишаємо тим самим: . Додавання виконано. Але неважко помітити, що отриманий дріб можна скоротити. Дійсно, чисельник отриманого дробу можна згорнути за формулою квадрат суми як (lgx+2) 2 (дивіться формули скороченого множення), таким чином, мають місце наступні перетворення: .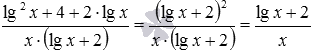

в) Дроби у сумі 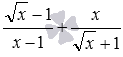мають різні знаменники. Але, перетворивши один із дробів, можна перейти до складання дробів з однаковими знаменниками. Покажемо два варіанти вирішення.

Перший метод. Знаменник першого дробу можна розкласти на множники, скориставшись формулою різниця квадратів, після чого скоротити цей дріб: 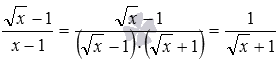. Таким чином, . Ще не завадить звільнитися від ірраціональності у знаменнику дробу: .

Другий спосіб. Множення числа і знаменника другого дробу (це вираз не звертається в нуль за жодних значень змінної x з ОДЗ для вихідного виразу) дозволяє досягти відразу двох цілей: звільнитися від ірраціональності і перейти до складання дробів з однаковими знаменниками. Маємо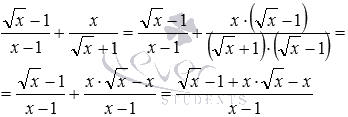

Відповідь:

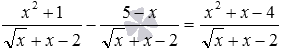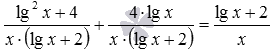а) , б) , в) .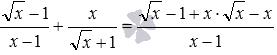

Останній приклад підвів нас до приведення дробів до спільного знаменника. Там ми майже випадково прийшли до однакових знаменників, спрощуючи один із дробів, що складаються. Але в більшості випадків при складанні та відніманні дробів з різними знаменниками доводиться цілеспрямовано приводити дроби до спільного знаменника. Для цього зазвичай знаменники дробів представляються у вигляді творів, беруться всі множники із знаменника першого дробу і до них додаються відсутні множники зі знаменника другого дробу.

приклад.

Виконати дії із дробами: а) 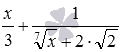, б) , в) .

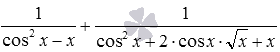Рішення.

а) Тут немає потреби щось робити зі знаменниками дробів. Як спільний знаменник беремо твір . У цьому випадку додатковим множником для першого дробу є вираз , а для другого дробу – число 3 . Ці додаткові множники приводять дроби до спільного знаменника, що надалі дозволяє виконати потрібну нам дію, маємо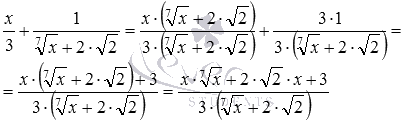

б) У цьому прикладі знаменники вже представлені у вигляді творів і жодних додаткових перетворень не вимагають. Очевидно, множники у знаменниках відрізняються лише показниками ступенів, тому, як спільний знаменник беремо добуток множників з найбільшими показниками, тобто, . Тоді додатковим множником для першого дробу буде x4, а для другого – ln(x+1). Тепер ми готові виконати віднімання дробів: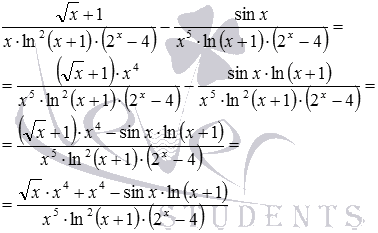

в) А в цьому випадку для початку попрацюємо зі знаменниками дробів. Формули різниця квадратів і квадрат суми дозволяють від вихідної суми перейти до виразу 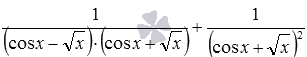. Тепер зрозуміло, що ці дроби можуть призвести до спільного знаменника . При такому підході рішення матиме такий вигляд: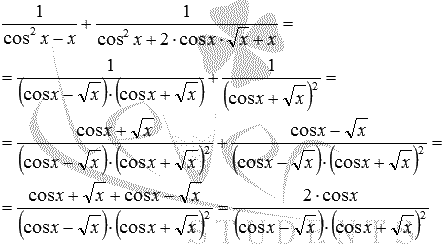

Відповідь:

а)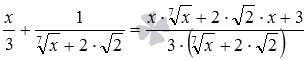

б)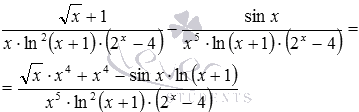

в)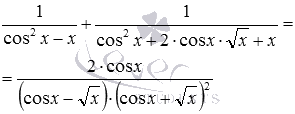

Приклади множення дробів із змінними

Множення дробів дає дріб, чисельник якого є добуток чисельників вихідних дробів, а знаменник – добуток знаменників. Тут, як бачите, все звично і просто, і можна лише додати, що отриманий в результаті виконання цієї дії дріб часто виявляється скоротимим. У цих випадках її скорочують, якщо, звичайно, це необхідно та виправдано.

У статті покажемо, як вирішувати дробина простих зрозумілих прикладах. Розберемося, що таке дріб і розглянемо вирішення дробів!

Концепція дробивводиться в курс математики, починаючи з 6 класу середньої школи.

Дроби мають вигляд: ±X/Y, де Y - знаменник, він повідомляє, на скільки частин розділили ціле, а X - чисельник, він повідомляє, скільки таких частин взяли. Для наочності візьмемо приклад із тортом:

У першому випадку торт розрізали порівну і взяли половину, тобто. 1/2. У другому випадку торт розрізали на 7 частин, у тому числі взяли 4 частини, тобто. 4/7.

Якщо частина від розподілу одного числа на інше не є цілим числом, її записують у вигляді дробу.

Наприклад, вираз 4:2 = 2 дає ціле число, а ось 4:7 націло не ділиться, тому такий вираз записується у вигляді дробу 4/7.

Іншими словами дріб- це вираз, який позначає розподіл двох чисел або виразів, який записується за допомогою дробової риси.

Якщо чисельник менший за знаменник - дріб є правильним, якщо навпаки - неправильним. До складу дробу може входити ціле число.

Наприклад, 5 цілих 3/4.

Цей запис означає, що для того, щоб отримати цілу 6, не вистачає однієї частини від чотирьох.

Якщо ви хочете запам'ятати, як вирішувати дроби за 6 клас, вам треба зрозуміти, що вирішення дробів, в основному, зводиться до розуміння кількох простих речей.

Дроби по суті це вираз частки. Тобто числове вираження того, яку частину становить це значення від одного цілого. Наприклад дріб 3/5 виражає, що, якщо ми поділили щось ціле на 5 частин і кількість часток або частин це цього цілого - три.
Дроб може бути менше 1, наприклад 1/2 (або по суті половина), тоді вона правильна. Якщо дріб більше 1, наприклад 3/2(три половини чи одне з половиною), вона неправильна й у спрощення рішення, нам краще виділити цілу частину 3/2= 1 ціла 1/2.
Дроби це такі ж числа, як 1, 3, 10, і навіть 100, тільки числа це не цілі, а дробові. З ними можна виконувати ті самі операції, що з числами. Вважати дроби не складніше, і на конкретних прикладах ми це покажемо.

Як вирішувати дроби. приклади.

До дробів застосовні найрізноманітніші арифметичні операції.

Приведення дробу до спільного знаменника

Наприклад, необхідно порівняти дроби 3/4 та 4/5.

Щоб розв'язати завдання, спочатку знайдемо найменший спільний знаменник, тобто. найменше число, яке ділиться без залишку на кожен із знаменників дробів

Найменший загальний знаменник(4,5) = 20

Потім знаменник обох дробів наводиться до найменшого спільного знаменника

Відповідь: 15/20

Додавання та віднімання дробів

Якщо потрібно порахувати суму двох дробів, їх спочатку призводять до спільного знаменника, потім складають чисельники, при цьому знаменник залишиться без змін. Різниця дробів вважається аналогічним чином, відмінність лише тому, що чисельники віднімаються.

Наприклад, необхідно знайти суму дробів 1/2 та 1/3

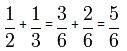
Тепер знайдемо різницю дробів 1/2 та 1/4

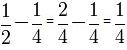
Множення та розподіл дробів

Тут розв'язання дробів нескладне, тут усе досить просто:

Множення - чисельники та знаменники дробів перемножуються між собою;
Поділ - спершу отримуємо дріб, обернений до другого дробу, тобто. міняємо місцями її чисельник та знаменник, після чого отримані дроби перемножуємо.

Наприклад:

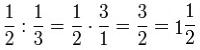
На цьому про те, як вирішувати дроби, Усе. Якщо у вас залишилися якісь питання щодо вирішенню дробівЩо то незрозуміло, то пишіть у коментарі і ми обов'язково вам відповімо.

Якщо ви вчитель, то можливо завантажити презентацію для початкової школи буде вам доречним.

Якщо матеріал був корисний, відблагорити наш сайт ви можете, зробивши пожертвування.
Будь-яку сумуна розвиток проекту ви можете

Подання раціонального дробу у вигляді суми найпростіших дробів

Основна властивість дробу

Умовимося вважати, що під "діями з дробами" на нашому уроці будуть розумітися дії звичайними дробами. Звичайний дріб - це дріб, що має такі атрибути, як чисельник, дробова риса і знаменник. Це відрізняє звичайний дріб від десяткового, який виходить із звичайної шляхом приведення знаменника до числа, кратного 10. Десятковий дрібзаписується з комою, що відокремлює цілу частину від дробової. У нас йтиметься про дії зі звичайними дробами, оскільки саме вони викликають найбільші труднощі у студентів, які забули основи цієї теми, пройденої у першій половині шкільного курсу математики. Разом про те при перетвореннях висловів у вищої математики застосовуються переважно саме події зі звичайними дробами. Одні скорочення дробів чого варті! Десяткові ж дроби особливих труднощів не викликають. Отже, вперед!

Два дроби і називаються рівними, якщо .

Наприклад, так як

Рівними також є дроби і (оскільки ), і (оскільки ).

Очевидно, рівними є дроби і . Це означає, що якщо чисельник і знаменник даного дробу помножити або розділити на те саме натуральне число, то вийде дріб, рівний даній: .

Ця властивість називається основною властивістю дробу.

Основну властивість дробу можна використовувати для зміни знаків у чисельнику та знаменника дробу. Якщо чисельник і знаменник дробу помножити на -1, отримаємо . Таким чином, значення дробу не зміниться, якщо одночасно змінити знаки у чисельнику та знаменника. Якщо ж змінити знак лише у чисельника або тільки у знаменника, то й дріб змінить свій знак:

Скорочення дробів

Користуючись основною властивістю дробу, можна замінити цей дрібіншим дробом, що дорівнює даної, але з меншим чисельником і знаменником. Таку заміну називають скороченням дробу.

Нехай, наприклад, дано дріб . Числа 36 та 48 мають найбільший спільний дільник 12. Тоді

У випадку скорочення дробу можливе завжди, якщо чисельник і знаменник є взаємно простими числами. Якщо чисельник і знаменник – взаємно прості числа, то дріб називається нескоротним.

Отже, скоротити дріб - це означає розділити чисельник та знаменник дробу на загальний множник. Все вищесказане можна застосувати і до дробових виразів, що містять змінні.

приклад 1.Скоротити дріб

Рішення. Для розкладання числа на множники, представивши попередньо одночлен - 5 xyу вигляді суми - 2 xy - 3xy, отримаємо

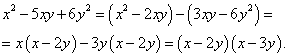
Для розкладання знаменника на множники використовуємо формулу різниці квадратів:

Таким чином,

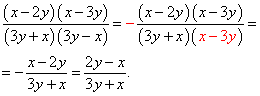
Приведення дробів до спільного знаменника

Нехай дані два дроби і . Вони мають різні знаменники: 5 і 7. Користуючись основною властивістю дробу, можна замінити ці дроби іншими, рівними їм, причому такими, що отримані дроби будуть однакові знаменники. Помноживши чисельник та знаменник дробу на 7, отримаємо

Помноживши чисельник та знаменник дробу на 5, отримаємо

Отже, дроби наведені до спільного знаменника:

Але це не єдине рішення поставленого завдання: наприклад, ці дроби можна привести також до спільного знаменника 70:

і взагалі до будь-якого знаменника, що ділиться одночасно на 5 та 7.

Розглянемо ще один приклад: приведемо до спільного знаменника дробу та . Розмірковуючи, як у попередньому прикладі, отримаємо

Але в цьому випадку можна привести дроби до спільного знаменника, меншого, ніж добуток знаменників цих дробів. Знайдемо найменше загальне кратне чисел 24 та 30: НОК(24, 30) = 120 .

Оскільки 120:4=5, те щоб записати дріб зі знаменником 120, треба і чисельник, і знаменник помножити на 5, це називається додатковим множником. Значить .

Далі отримуємо 120:30=4. Помноживши чисельник та знаменник дробу на додатковий множник 4, отримаємо .

Отже, ці дроби приведені до спільного знаменника.

Найменше загальне кратне знаменників цих дробів є найменшим можливим загальним знаменником.

Для дробових виразів, В які входять змінні, спільним знаменником є многочлен, який ділиться на знаменник кожного дробу.

Тепер, коли ми навчилися складати та множити окремі дроби, можна розглядати складніші конструкції. Наприклад, що, якщо в одному завданні зустрічається і додавання, і віднімання, і множення дробів?

Насамперед треба перевести всі дроби в неправильні. Потім послідовно виконуємо необхідні дії - у тому порядку, як і для звичайних чисел. А саме:

Спочатку виконується зведення в ступінь - позбавтеся всіх виразів, що містять показники;
Потім - розподіл та множення;
Останнім кроком виконується складання та віднімання.

Зрозуміло, якщо у вираженні присутні дужки, порядок дій змінюється – все, що стоїть усередині дужок, треба рахувати насамперед. І пам'ятайте про неправильні дроби: виділяти цілу частину треба лише тоді, коли всі інші дії вже виконані.

Перекладемо всі дроби з першого виразу в неправильні, а потім виконаємо дії:

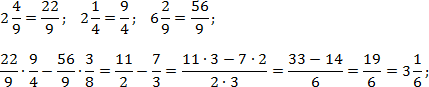
Тепер знайдемо значення другого виразу. Тут дробів із цілою частиною немає, але є дужки, тому спочатку виконуємо складання, і лише потім – розподіл. Зауважимо, що 14 = 7 · 2. Тоді:

Зрештою, вважаємо третій приклад. Тут є дужки та ступінь – їх краще рахувати окремо. Враховуючи, що 9 = 3 · 3 маємо:

Зверніть увагу на останній приклад. Щоб звести дріб у ступінь, треба окремо звести в цей ступінь чисельник, і окремо – знаменник.

Можна вирішувати інакше. Якщо згадати визначення ступеня, завдання зведеться до звичайному множеннюдробів:

Багатоповерхові дроби

Досі ми розглядали лише «чисті» дроби, коли чисельник і знаменник є прості числа. Це цілком відповідає визначенню числового дробу, даному в першому уроці.

Але що, якщо в чисельнику чи знаменнику розмістити складніший об'єкт? Наприклад, іншу числовий дріб? Такі конструкції виникають досить часто, особливо під час роботи з довгими виразами. Ось кілька прикладів:

Правило роботи з багатоповерховими дробами лише одне: їх треба негайно позбавлятися. Видалити «зайві» поверхи досить просто, якщо згадати, що дробова риса означає стандартну операцію поділу. Тому будь-який дріб можна переписати так:

Користуючись цим фактом і дотримуючись порядку дій, ми легко зведемо будь-який багатоповерховий дріб до звичайного. Погляньте на приклади:

Завдання. Перекладіть багатоповерхові дроби у звичайні:

У кожному випадку перепишемо основний дріб, замінивши роздільну межу знаком розподілу. Також згадаємо, що будь-яке ціле число представимо у вигляді дробу зі знаменником 1. Тобто. 12 = 12/1; 3 = 3/1. Отримуємо:

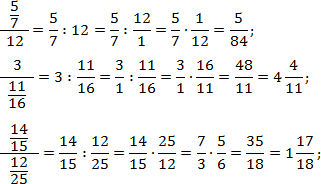
В останньому прикладі перед остаточним множенням дробу було скорочено.

Специфіка роботи з багатоповерховими дробами

У багатоповерхових дробах є одна тонкість, яку завжди треба пам'ятати, інакше можна отримати неправильну відповідь, навіть якщо всі обчислення були правильними. Погляньте:

У чисельнику стоїть окреме число 7, а знаменнику - дріб 12/5;
У чисельнику стоїть дріб 7/12, а знаменнику - окреме число 5.

Отже, для одного запису отримали дві абсолютно різні інтерпретації. Якщо підрахувати, відповіді також будуть різними:

Щоб запис завжди читався однозначно, використовуйте просте правило: риса основного дробу, що розділяє, повинна бути довшою, ніж риса вкладеної. Бажано – у кілька разів.

Якщо дотримуватися цього правила, то наведені вище дроби треба записати так:

Так, можливо, це негарно і займає дуже багато місця. Зате ви вважатимете правильно. Насамкінець - пара прикладів, де дійсно виникають багатоповерхові дроби:

Завдання. Знайдіть значення виразів:

Отже, працюємо з першим прикладом. Перекладемо всі дроби в неправильні, а потім виконаємо операції додавання та поділу:

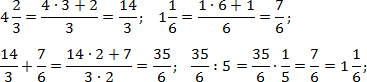
Аналогічно надійдемо з другим прикладом. Перекладемо всі дроби в неправильні та виконаємо необхідні операції. Щоб не втомлювати читача, я опущу деякі явні викладки. Маємо:

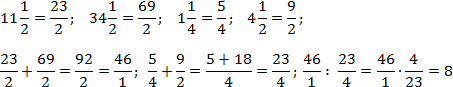
Завдяки тому, що в чисельнику та знаменнику основних дробів стоять суми, правило запису багатоповерхових дробівдотримується автоматично. Крім того, в останньому прикладі ми навмисно залишили число 46/1 у формі дробу, щоб виконати поділ.

Також зазначу, що в обох прикладах дробова риса фактично замінює дужки: насамперед ми знаходили суму, і лише потім – приватне.

Хтось скаже, що перехід до неправильним дробаму другому прикладі був явно надлишковим. Можливо так воно і є. Але цим ми страхуємо себе від помилок, адже наступного разу приклад може бути набагато складнішим. Вибирайте самі, що важливіше: швидкість чи надійність.