Як вирішувати алгебраїчні дроби із різними знаменниками. Складання та віднімання алгебраїчних дробів з різними знаменниками. Приведення алгебраїчних дробів до спільного знаменника
Відеоурок «Складання та віднімання алгебраїчних дробівз різними знаменниками» є наочним посібником, за допомогою якого дається теоретичний матеріал, докладно пояснюються алгоритми та особливості виконання операцій віднімання, складання дробів, що мають різні знаменники. За допомогою посібника вчителю легше сформувати вміння учнів виконувати операції з дробами алгебри. У ході відеоуроку розглядається ряд прикладів, розв'язання яких описується докладно, зважаючи на важливі деталі.
Змінні використовуються в математиці для позначення довільних чи невідомих чисел. Описати використання змінних у математиці. Змінні, як правило, є алфавітними символами, які представляють числа та корисні в математиці для кількох цілей. Параметри рівнянь часто позначаються змінними та є частиною даної інформації у рівнянні. В елементарній математиці змінна - це алфавітний символ, що представляє число, яке називається значенням змінної, яке довільно, не повністю визначене або невідоме.
Застосування відеоуроку під час уроку математики дає можливість вчителю швидше досягти навчальних цілей, підвищити ефективність навчання. Наочність демонстрації допомагає учням запам'ятати матеріал, глибше його освоїти, тому відео можна використовувати, супроводжуючи пояснення вчителя. Якщо це відео використовується як частина уроку, то звільняється час вчителя посилення індивідуальної роботи та використання інших інструментів навчання підвищення ефективності навчання.
Приклади застосування правила для звичайних дробів
Змінні корисні з кількох причин. Змінні можуть являти числа, значення яких ще не відомі. Змінні можуть описувати математичні відносини між величинами, що змінюються. Змінні можуть описувати загальні проблеми без зазначення значень відповідних величин.
Змінні можуть описувати деякі математичні характеристики. Наприклад, основною властивістю додавання є комутативність, яка стверджує, що порядок чисел, що додаються разом, не має значення. Змінні можуть бути використані для представлення різних типів чисел. Загальноприйнято, що багато змінних з'являються в одній і тій же математичній формулі, і вони можуть відігравати різні ролі. Деякі імена або кваліфікатори були введені, щоб відрізнити їх.
Демонстрація починається з представлення теми уроку. Зазначається, що виконання операцій віднімання, складання алгебраїчних дробів аналогічно до виконання операцій з звичайними дробами. Нагадується механізм віднімання, складання для звичайних дробів - наводяться дроби до спільного знаменника, потім виконуються самі операції.
Чотири з них є заданими числами, які називаються параметрами рівняння. Останнє, х, є рішенням рівняння, яке невідоме і має бути вирішене для. Зверніть увагу, що термін рівняння є будь-яким значенням або виразом, який відділений від іншого члена пробілом або символом. Отже, термін може просто бути константою або змінною або може містити як коефіцієнт, так і невідому змінну.
Додавання та віднімання алгебраїчних виразів
Проте це не завжди так. Спрощення алгебраїчних виразів пов'язані з об'єднанням подібних термінів, часто з допомогою додавання і віднімання. Використовуйте поняття подібних термінів для додавання та віднімання виразів, що містять змінні. «Подібні терміни» - це терміни в виразах алгебри, які є константами або включають одні і ті ж змінні, підняті до однакових показників. Як терміни: сутності, які включають одні й самі змінні, підняті до однакових показників. Кожне вираз алгебри складається з одного або декількох членів.
Озвучується та описується на екрані алгоритм віднімання, складання алгебраїчних дробів. Він складається з двох кроків - приведення дробів до однакових знаменників і потім виконання додавання (або віднімання) дробів з рівними знаменниками. Застосування алгоритму розглядається з прикладу знаходження значень виразів a/4b 2 -a 2 /6b 3 , і навіть x/(х+у)-x/(х-у). Зазначається, що для вирішення першого прикладу необхідно привести обидва дроби до одного знаменника. Цим знаменником буде 12b3. Приведення даних дробів до знаменника 12b 3 докладно розглядалося у минулому відеоуроку. В результаті перетворення виходить два дроби з рівними знаменниками 3ab/12b3 і 2a2/12b3. Ці дроби складаються відповідно до правила складання дробів із рівними знаменниками. Після складання чисельників дробів у результаті виходить дріб (3ab+2a 2)/12b 3 . Далі описується рішення прикладу х/(x+у)-x/(х-у). Після приведення дробів до одного знаменника виходять дроби (х 2 -ху)/(х 2 -у 2) та (х 2 +ху)/(х 2 -у 2). Відповідно до правила віднімання дробів з рівними знаменниками, робимо операцію з чисельниками, після чого виходить дріб -2ху/(х 2 -у 2).
Терміни у цих виразах поділяються операторами або -. Терміни називаються як терміни, якщо вони включають одні й ті самі змінні та показники. Усі константи також схожі на терміни. Крім того, такі приклади таких термінів. Зверніть увагу на те, що терміни, які поділяють змінну, але не експоненту, не схожі на терміни. Аналогічно терміни, які поділяють експоненту, але мають різні змінні, не схожі на терміни. Ми можемо спростити вираз алгебри, об'єднуючи подібні члени.
Вирази з більш ніж двома умовами
По-перше, давайте напишемо обидва терміни як додаткові проблеми. Додаючи ці терміни разом, ми маємо. Якщо вираз містить більше двох термінів, може бути корисним переставити терміни так, щоб такі члени були разом. Комутативне властивість додавання свідчить, що ми можемо змінити порядок членів без зміни значення висловлювання. Отже, ми можемо змінити порядок наступного висловлювання, як намагатися об'єднати такі висловлювання.
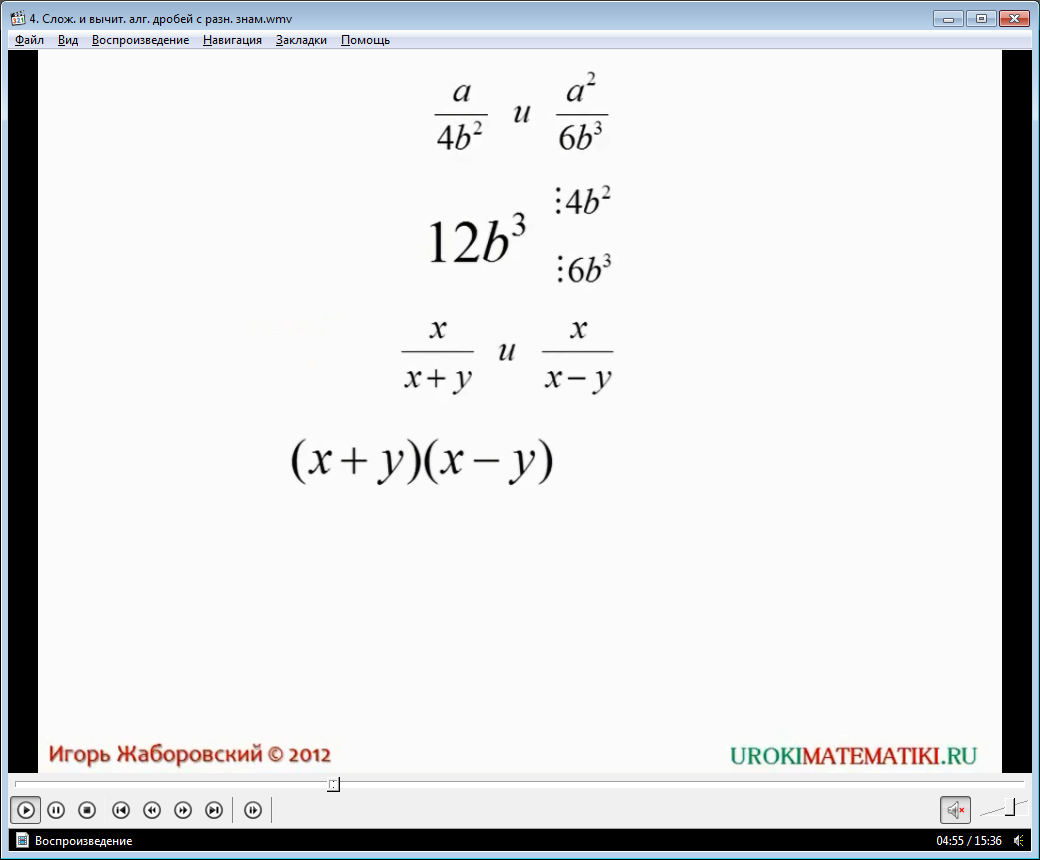
Зазначається, що найважчим кроком у вирішенні завдань на додавання, віднімання дробів, що мають різні знаменники, є приведення їх до спільного знаменника. Робляться підказки, як легко виробити навички у вирішенні цих завдань. Розбирається загальний знаменник дробу. Він складається з числового коефіцієнта зі змінною, зведеною до ступеня. Видно, що вираз може поділятися на знаменники першого та другого дробів. При цьому числовий коефіцієнт 12 є найменшим загальним кратним числових коефіцієнтів дробів 4 і 6. А змінну b містять обидва знаменники 4b 2 і 6b 3 . При цьому в загальному знаменнику міститься змінна найбільше серед знаменників вихідних дробів. Також розглядається знаходження спільного знаменника для х/(x+у) та x/(х-у). Зазначається, що спільний знаменник (x+у)(x-у) поділяється на кожен знаменник. Отже, вирішення завдання зводиться до знаходження найменшого загального кратного наявних числових коефіцієнтів, а також знаходження вищого показника ступеня для літерної змінної, що зустрічається кілька разів. Потім після збирання цих частин у загальний твір виходить спільний знаменник.
Ми хочемо змінити вираз для угруповання як доданки. Тепер ми зможемо легко додати схожі вирази, щоб спростити вираз. Ті ж правила застосовуються, коли вираз включає віднімання. Однак будьте обережні: при зміні порядку термінів ви гарантуєте, що знак мінус слідує за терміном, до якого він належить. Цей вираз правильно переупорядкований і спрощений таким чином. Таким чином є три кроки до об'єднання таких термінів.
Вирівняйте вираз так, щоб аналогічні терміни групувалися разом. Додайте або відніміть коефіцієнти схожих термінів до тих пір, поки не буде якнайменше кожного типу терміна. Тепер згрупуйте ці схожі терміни разом. Додайте та відніміть коефіцієнти подібних термінів.
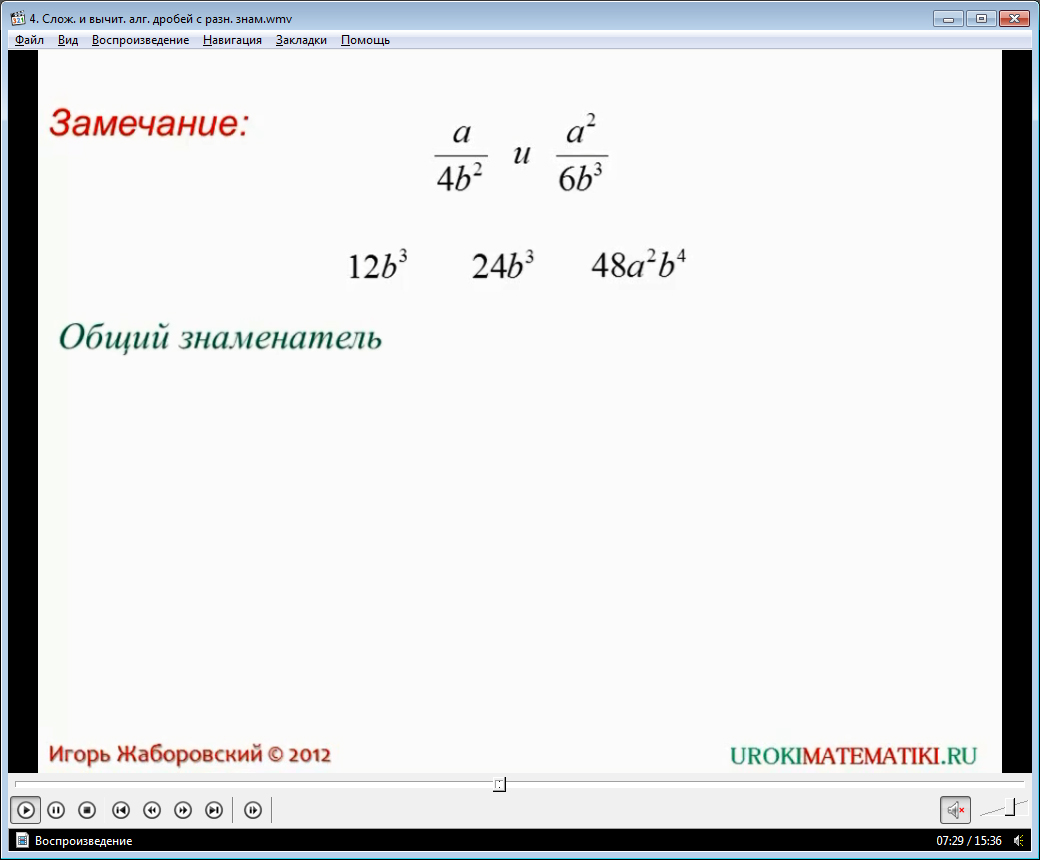
Озвучується і формулюється на екрані алгоритм знаходження кількох дробів загального знаменника. Цей алгоритм складається з чотирьох етапів, у першому з яких знаменники розкладаються на множники. На другому етапі алгоритму знаходиться найменше загальне кратне наявних даних коефіцієнтів, що входять до складу знаменників дробів. На третьому етапі складається твір, до складу якого входять літерні множники розкладів знаменників, у своїй літерний показник, що у кількох знаменниках, вибирається найбільшою мірою. На четвертому етапі числові та літерні множники, знайдені на попередніх етапах, збираються в один твір. Це буде спільний знаменник. До розглянутого алгоритму робиться зауваження. У прикладі знаходження загального знаменника дробів a/4b 2 і a 2 /6b 3 зазначається, що крім 12b 3 є інші знаменники 24b 3 і 48a 2 b 3 . І для кожної множини дробів можна знайти багато спільних знаменників. Однак знаменник 12b 3 є найпростішим і зручнішим, тому його називають найменшим загальним знаменником вихідних дробів. Додаткові множники є результатом приватного загального знаменника і вихідного знаменника дробу. Детально демонструється за допомогою анімації, як чисельник, знаменник дробів множиться на додатковий множник.
Збільшення алгебраїчних виразів
Спростіть такий вираз. Додайте та відніміть коефіцієнти аналогічних термінів. Процес множення алгебраїчних виразів відрізняється одночленів і многочленов. Обчислити добуток виразів, що містять змінні.
Розмноження двох одночленів
Моном - це один член, що складається з добутку чисел та змінних. Він є відносним поліномом, який є виразом алгебри з більш ніж одним членом. Нижче наведено приклади одночленів.Розмноження мономів та багаточленів
Коли ви множите мономи, ви множите їх цілі коефіцієнти разом і, якщо вони містять які-небудь з одних і тих же змінних, додайте експоненти по цих змінних разом. Моном можна помножити на багаточлен будь-якого розміру. Моном слід множити на кожен член у багаточлен окремо. Будь-який негативний знак у терміні має бути включений до множення цього терміна. Отримуваний багаточлен матиме таку ж кількість членів, що й поліном у завданні.
Далі пропонується розглянути алгоритм приведення до спільного знаменника алгебраїчних дробів у простішій формі, щоб він був зрозумілішим для учнів. Він також складається з чотирьох етапів, у першому з яких розкладання знаменників на множники. Потім пропонується з першого знаменника виписати всі множники, з інших знаменників добуток доповнити відсутніми множниками. Таким чином, знаходиться спільний знаменник. Знаходяться додаткові множники до кожного дробу з тих множників знаменника, що не потрапили до загального знаменника. Четвертим кроком є визначення кожного дробу нового чисельника, що є твором старого чисельника і додаткового множника. Потім кожен дріб записується з новим чисельником та знаменником.
Розмноження двох біномів
Перший зовнішній. . Як тільки цей процес буде завершено, всі результуючі члени будуть об'єднані в один член. Пам'ятайте, що будь-який негативний знак у терміні біномії також повинен бути включений до множення цього терміна. Крім того, не забудьте спростити отриманий поліном, якщо це можливо, шляхом поєднання подібних термінів.
Приклад множення біномів
Помножте такі біноми. Тепер додайте всі ці терміни разом. Зауважте, що два з цих термінів схожі на терміни і тому можуть бути додані разом, щоб спростити вираз далі.
Спрощення радикальних виразів
Радикальне вираз, що містить змінні, часто може бути спрощено до більш основного виразу, так само як вирази, що містять лише цілі числа.У наступному прикладі описується спрощення виразу 3а/(4а 2 -1)-(а+1)/(2а 2 +а). На першому етапі рішення знаменники кожного дробу розкладаються на множники. Для творів спільним множникомє (2а+1). Доповнивши твір множниками (2а-1) і а, виходить загальний знаменник виду а(2а-1)(2а+1). Будується допоміжна таблиця, у якій вказуються загальний знаменник, знаменники, додаткові множники. На другому етапі рішення кожен чисельник множиться на додатковий множник, виконується віднімання. В результаті виходить дріб (а 2-а+1)/а(2а-1)(2а+1).
Спростити радикальні вирази, які містять змінні. Якщо радикал повністю спрощений, немає жодного фактора радикала, який може бути записаний як потужність, більший або рівний індексу, немає жодних фракцій під знаком радикала, і в знаменнику немає радикалів. Коли радикальні висловлювання містять змінні, їх спрощення слід тому самому процесу, що й у виразів, містять лише цілі числа. Аналогічним чином правила множення та поділу радикальних виразів, як і раніше, застосовуються, коли вирази містять змінні. Простіше кажучи число під символом кореня. . Вирази, які включають коріння, відомі як радикальні вирази.

У прикладі 3 розглядається спрощення виразу b/(2a 4 +4a 3 b+2a 2 b 2)-1/(3ab 2 -3a 3)+b/(6a 4 -6a 3 b). Рішення також розбирається за етапами, звертається увага на суттєві особливості виконання операцій, докладно описується приведення дробів до спільного знаменника, виконання операцій із чисельником. В результаті обчислень та після перетворення виходить дріб (2а 3 +6а 2 b-ab 2 +b 3)/6a 3 (a-b)(a+b) 2 .
Корінь ступеня 2 називається квадратним коренем; корінь ступеня 3 називається кубічним коренем. Коріння вищих ступенів згадується з використанням порядкових чисел. Радикальне вираз називається спрощеним, якщо. Немає фактора радіусу, який може бути записаний як потужність, більший або рівний індексу, при знаку радикала немає фракцій, і знаменника немає радикалів. Спочатку знайдіть ідеальний квадрат під знаком квадратного кореня та видаліть його. Потім поділіть фракцію під знаком радикала.
Радикальні вирази зі змінними
Нарешті, видаліть радикал зі знаменника. Для спрощення радикальні вирази, що містять змінні, обробляються інакше, ніж вирази, що містять цілі числа. Наприклад, розглянемо таке. Це слідує тій же логіці, яку ми використовували вище, при спрощенні радикального вираження цілими числами.
Відеоурок «Складання та віднімання алгебраїчних дробів з різними знаменниками» може стати засобом підвищення ефективності уроку математики на цю тему. Посібник стане у нагоді вчителю, який здійснює дистанційне навчання, для наочного представлення навчального матеріалу. Учням відеоурок може бути рекомендованим для самостійного навчання, тому що в ньому докладно і зрозуміло пояснюються особливості виконання операцій, що вивчаються.
По-перше, зверніть увагу на те, що квадратний квадратний коріньмає ідеальний квадрат, та витягніть його. Нагадаємо, що ми можемо переписати чисельник та знаменник у вигляді раціональної експоненти, що дозволить нам продовжити правило розподілу. Зверніть увагу, що показник у знаменнику можна спростити, тому маємо.
Правила для роботи з числами з показниками можуть бути застосовані до змінних з показниками
Нагадаємо правило розподілу чисел з показниками, у яких віднімаються показники. Застосування правила розподілу дає. Спростити експонентні вирази, що містять змінні. Правила роботи з експоненціальними виразами однакові для виразів зі змінними, як і для тих, які мають тільки цілі числа.
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання. Усі матеріали перевірені антивірусною програмою.
Розвиваючі та навчальні посібники в інтернет-магазині "Інтеграл"
Посібник до підручника Муравіна Г.К. Посібник до підручника Макарічева Ю.М.
Нагадаємо правила роботи з числами з показниками, що використовуються при спрощенні та вирішенні задач математики. Однак вони також застосовуються до виразів, що включають комбінацію цілих чисел, так і змінних.
- Правила експонентних виразів.
- Раніше ми застосовували ці правила лише до виразів із цілими числами.
- Це робить їх більш широко застосовними під час вирішення математичних завдань.
Основні властивості алгебраїчних дробів
З погляду проведення операцій експоненційні висловлювання, що містять змінні, розглядаються як і, якби вони складалися з цілих чисел. Наприклад, розглянемо правило множення двох чисел із показниками. Це ж правило застосовується до виразів зі змінними. Отже, зберігаються такі твердження. Кожне з інших правил роботи з числами відноситься також до виразів зі змінними. Ви побачите, як кожен із них застосовується в наступних прикладах. . Тепер застосуємо правило для розподілу експоненційних виразів на ту саму базу.
Що таке алгебраїчний дріб?
Алгебраїчна дріб - це вираз виду: $ \ frac (P) (Q) $.
Де:
P - чисельник алгебраїчного дробу.
Q - знаменник алгебраїчного дробу.
Наведемо приклади алгебраїчних дробів:
$\frac(a)(b)$, $\frac(12)(q-p)$, $\frac(7y-4)(y)$.
Основні властивості алгебраїчних дробів
Властивість 1.І чисельник і знаменник дробу можна помножити на те саме число (або на одночлен, або на многочлен). У результаті, ми отримаємо той самий дріб, але представлений в іншому вигляді.
Інакше це перетворення називається тотожним. Його використовують, щоб привести алгебраїчне (і не тільки) вираз до більш простого вигляду, і робота з цим виразом буде зручнішою.
Щоб спростити першу частину виразу, застосуйте правило для множення двох експонентних виразів на ту саму базу. Щоб спростити другу частину виразу, застосовуйте правило для множення чисел із показниками. Ми також можемо застосувати правило підвищення потужності до іншого показника. Поєднуючи два терміни, наш оригінальний вираз спрощує.
Раціональні алгебраїчні вирази. Додавання і віднімання раціональних виразів пов'язані тими самими правилами, як і додавання і віднімання дробів. Маніпулювати раціональними виразами, що містять змінні. Завжди робіть раціональні висловлювання перед тим, як робити щось ще. Коли два раціональні виразидодаються або віднімаються один з одного, кожен спочатку повинен бути помножений на деяку константу, так що обидва вирази мають один і той самий знаменник. Коли два раціональних вирази мають той самий знаменник, їх чисельники можуть бути об'єднані.
$\frac(a)(4b^2)=\frac(a*3b)(4b^2*3b)=\frac(3ab)(12b^3)$.
І чисельник та знаменник ми помножили на одночлен $3b$. У результаті у нас вийшов дріб, тотожний вихідний.
$\frac(a^2)(6b^3)=\frac(a^2*2)(6b^3*2)=\frac(2a^2)(12b^3)$.
За необхідності алгебраїчну дроб можна помножити на просте число. У цьому прикладі і чисельник і знаменник ми помножили на число 2. І знову ми отримали дріб, тотожний вихідний.
Властивість 2.
І чисельник, і знаменник дробу можна розділити на те саме число (або одночлен, або многочлен). У результаті ми отримаємо той самий дріб, але представлений в іншому вигляді.
Як і у випадку з множенням, до такого тотожного перетворення вдаються, щоб уявити дріб у більш простому виглядіта полегшити роботу з нею.
Додавання та віднімання алгебраїчних дробів з однаковими знаменниками
Якщо у алгебраїчних дробів однакові знаменники, їх складають, як прості дроби (складають лише чисельники, а знаменник залишається загальним).Загальне правило:
$frac(a)(d)+frac(b)(d)-frac(c)(d)=frac(a+b-c)(d)$.
приклад.
Спростіть вираз:
$\frac(2a^2+5)(a^2-ab)+\frac(2ab+b)(a^2-ab)-\frac(b+5)(a^2-ab)$.
Рішення.
Використовуємо правило додавання дробів про яке розказано вище, тобто складемо чисельники, а знаменник запишемо загальний.
$\frac(2a^2+5)(a^2-ab)+\frac(2ab+b)(a^2-ab)-\frac(b+5)(a^2-ab)=\frac ((2a^2+5)+(2ab+b)-(b+5))(a^2-ab)$.
Попрацюємо з чисельником.
$(2a^2+5)+(2ab+b)-(b+5)=$
$2a^2+5+2ab+b-b-5=2a^2+2ab$.
В результаті отримуємо дріб:
$\frac(2a^2+2ab)(a^2-ab)$.
Хлопці перед тим, як закінчити рішення, перевірте: чи не можна ще спростити отриманий результат. Адже в цьому полягає весь сенс перетворення – спростити вираз.
Якщо уважно подивитися, то можна зрозуміти, що отриманий дріб можна ще спростити.
$\frac(2a^2+2ab)(a^2-ab)=\frac(2a(a+b))(a(a-b))=\frac(2(a+b))(a-b)=\ frac(2a+2b)(a-b)$.
Додавання та віднімання алгебраїчних дробів з різними знаменниками
При додаванні алгебраїчних дробів з різними знаменниками треба діяти як і, як із роботі з звичайними дробами. Спочатку потрібно привести дріб до спільного знаменника, а за тим скласти або відняти чисельники дробів, відповідно до загальним правиломМи розглянули.приклад.
Обчисліть:
$\frac(a)(4b^2)+\frac(a^2)(6b^3)$.
Рішення.
Наведемо ці дроби до спільного знаменника. У цьому прикладі спільним знаменником є одночлен $12b^3$.
Тоді.
$\frac(a)(4b^2)+\frac(a^2)(6b^3)=\frac(3ab)(12b^3)+\frac(2a^2)(12b^3)=
\frac(3ab+2a^2)(12b^3)$.
Найскладніше – це знаходження спільного знаменника для дробів. У деяких випадках це не просте завдання.
При знаходженні спільного знаменника можна дотримуватись правил:
1. Якщо обидва знаменники є одночленами без дужок, то краще спочатку підібрати загальний знаменник для числа, а потім - для змінної. У прикладі число - 12, а змінна - $b^3$.
2. Якщо знаменник є складнішим виразом, наприклад, $х + 1$, $x +y$ тощо, то краще підібрати знаменник у вигляді твору знаменників, наприклад, $(х + у)(х - у) $. Такий знаменник ділиться і на $х+у$, і на $х – у$.
Запам'ятайте!
Для двох алгебраїчних дробів спільних знаменників можна підібрати скільки завгодно. Але для спрощення розрахунків, потрібно вибрати найпростіший із можливих.


