Квадратичний корінь. Арифметичний квадратний корінь

Невід'ємний квадратний коріньз позитивного числаназивається арифметичним квадратним коренемта позначається з використанням знака радикала.

Комплексні числа

Над полем комплексних чисел рішень завжди два, що відрізняються лише знаком (за винятком квадратного кореня з нуля). Корінь із комплексного числа часто позначають як , проте використовувати це позначення потрібно обережно. Поширена помилка:

Для отримання квадратного кореня з комплексного числа зручно використовувати експоненційну форму запису комплексного числа: якщо

де корінь з модуля розуміється в сенсі арифметичного значення, а k може приймати значення k = 0 і k = 1, таким чином у відповіді виходять два різні результати.

Узагальнення

Квадратне коріння вводиться як рішення рівнянь виду і для інших об'єктів: матриць, функцій, операторів і т. п. Як операцію при цьому можуть використовуватися досить довільні мультиплікативні операції, наприклад, суперпозиція.

Квадратний корінь в інформатиці

Багато мовах програмування функціонального рівня (а також мовами розмітки типу LaTeX) функція квадратного кореня позначається як sqrt(Від англ. square root"квадратний корінь").

Алгоритми знаходження квадратного кореня

Знаходження чи обчислення квадратного кореня заданого числа називається вилученням(квадратного) кореня.

Розкладання в ряд Тейлора

Арифметичне вилучення квадратного кореня

Для квадратів чисел вірні такі рівності:

Тобто, дізнатися цілу частину квадратного кореня числа можна, віднімаючи з нього всі непарні числа по порядку, поки залишок не стане менше наступного числа, що віднімається або дорівнює нулю, і порахувавши кількість виконаних дій. Наприклад, так:

Виконано 3 дії, квадратний корінь числа 9 дорівнює 3.

Недоліком такого способу є те, що якщо видобутий корінь не є цілим числом, можна дізнатися тільки його цілу частину, але не точніше. У той самий час такий спосіб цілком доступний дітям, вирішальним найпростіші математичні завдання, які вимагають вилучення квадратного кореня.

Груба оцінка

Багато алгоритмів обчислення квадратного корінняз позитивного дійсного числа Sвимагають деякого початкового значення. Якщо початкове значення надто далеке від реального значення кореня, обчислення сповільнюються. Тому корисно мати грубу оцінку, яка може бути дуже неточною, але легко обчислюється. Якщо S≥ 1, нехай Dбуде числом цифр Sліворуч від десяткової коми. Якщо S < 1, пусть Dбуде числом нулів, що йдуть поспіль, праворуч від десяткової коми, взяте зі знаком мінус. Тоді груба оцінка виглядає так:

Якщо Dнепарно, D = 2n+ 1, тоді використовуємо Якщо Dпарно, D = 2n+ 2, тоді використовуємо

Два та шість використовуються тому, що і

При роботі в двійковій системі (як усередині комп'ютерів) слід використовувати іншу оцінку (тут Dце число двійкових цифр.

Геометричне вилучення квадратного кореня

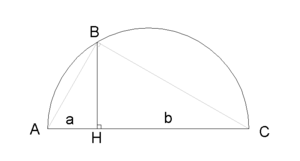
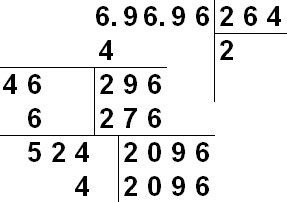
Для ручного вилучення кореня застосовується запис, схожа на поділ стовпчиком. Виписується число, коріння якого шукаємо. Праворуч від нього поступово отримуватимемо цифри шуканого кореня. Нехай витягується корінь із числа з кінцевим числом знаків після коми. Для початку подумки чи мітками розіб'ємо число N на групи по дві цифри ліворуч і праворуч від десяткової точки. При необхідності групи доповнюються нулями - ціла частина доповнюється зліва, дробова справа. Так 31234.567 можна уявити, як 03 12 34 . 56 70. На відміну від розподілу знос проводиться такими групами по 2 цифри.

Наочний опис алгоритму:

Серед безлічі знань, які є ознакою грамотності, на першому місці стоїть абетка. Наступним, таким самим «знаковим» елементом, є навички складання-множення і, що примикають до них, але зворотні за змістом, арифметичні операції віднімання-поділу. Засвоєні в далекому шкільному дитинстві навички, служать вірою і правдою вдень і вночі: ТБ, газета, СМС, І всюди читаємо, пишемо, вважаємо, складаємо, віднімаємо, множимо. А, скажіть, чи часто вам доводилося жити, витягувати коріння, крім як на дачі? Наприклад, таке цікаве завдання, типу, корінь квадратний з числа 12345 ... Є ще порох в порохівницях? Здолаємо? Та немає нічого простішого! Де тут мій калькулятор ... А без нього, врукопашну, слабко?

Спочатку уточнимо, що це таке - квадратний корінь числа. Взагалі кажучи, «витягти корінь із числа» означає виконати арифметичну дію протилежне зведенню в ступінь – ось вам і єдність протилежностей у життєвому додатку. припустимо, квадрат, це множення числа на себе, тобто, як вчили в школі, Х * Х = А або в іншому записі Х2 = А, а словами - «Х у квадраті дорівнює А». Тоді обернена задача звучить так: квадратний корінь числа А, являє собою число Х, яке, будучи зведене в квадрат, дорівнює А.

Вилучаємо квадратний корінь

Зі шкільного курсу арифметики відомі способи обчислень «у стовпчик», які допомагають виконати будь-які підрахунки із застосуванням перших чотирьох арифметичних дій. На жаль… Для квадратних, і не лише квадратних, коріння таких алгоритмів не існує. А в такому разі як витягти квадратний корінь без калькулятора? З визначення квадратного кореня висновок один - необхідно підбирати значення результату послідовним перебором чисел, квадрат яких наближається до значення підкореного виразу. Тільки і всього! Не встигне пройти годину-другу, як можна порахувати, використовуючи добре відомий прийом множення в «стовпчик», будь-який квадратний корінь. За наявності навичок для цього достатньо кількох хвилин. Навіть не зовсім просунутий користувач калькулятора чи ПК робить це одним махом – прогрес.

Якщо серйозно, то обчислення квадратного кореня часто виконують, використовуючи прийом «артилерійської вилки»: спочатку беруть число, квадрат якого, приблизно, відповідає підкореному вираженню. Краще, якщо «наш квадрат» трохи менший за цей вислів. Потім коригують число за власним вмінням-розумінням, наприклад, множать на два, і... знову зводять у квадрат. Якщо результат більший за число під коренем, послідовно коригуючи вихідне число, поступово наближаються до його «колеги» під коренем. Як бачите - жодного калькулятора, тільки вміння рахувати «в стовпчик». Звичайно ж, є безліч науково-аргументованих та оптимізованих алгоритмів обчислень квадратного кореня, але для домашнього застосування зазначений вище прийом дає 100% впевненість у результаті.

Так, мало не забув, щоб підтвердити свою збільшену грамотність, обчислимо квадратний корінь раніше зазначеного числа 12345. Робимо покроково:

1. Візьмемо, суто інтуїтивно, Х = 100. Підрахуємо: Х * Х = 10000. Інтуїція на висоті – результат менше 12345.

2. Спробуємо, теж чисто інтуїтивно, Х = 120. Тоді: Х * Х = 14400. І знову з інтуїцією порядок – результат більше 12345.

3. Вище отримана «вилка» 100 та 120. Виберемо нові числа – 110 та 115. Отримуємо, відповідно, 12100 та 13225 – вилка звужується.

4. Пробуємо на "можна" Х = 111. Отримуємо Х * Х = 12321. Це число вже досить близько до 12345. Відповідно до необхідної точності «підганяння» можна продовжити або зупинитися на отриманому результаті. От і все. Як і було обіцяно – все дуже просто та без калькулятора.

Зовсім небагато історії…

Додумалися до використання квадратного коріння ще піфагорійці, учні школи та послідовники Піфагора, за 800 років до н.е. і відразу, «нарвалися» на нові відкриття області чисел. І звідки що?

1. Розв'язання задачі із вилученням кореня, дає результат у вигляді чисел нового класу. Їх назвали ірраціональними, інакше кажучи, "нерозумними", т.к. вони не записуються закінченим числом. Найкласичніший приклад такого роду - квадратний корінь з 2. Цей випадок відповідає обчисленню діагоналі квадрата зі стороною, що дорівнює 1 - ось воно, вплив школи Піфагора. Виявилося, що у трикутника з цілком конкретним одиничним розміром сторін, гіпотенуза має розмір, що виражається числом, у якого немає кінця. Так у математиці з'явилися

2. Відомо, що Виявилося, що ця математична операція містить ще один каверз - витягуючи корінь, ми не знаємо, квадратом якого числа, позитивного або негативного, є підкорене вираз. Ця невизначеність, подвійний результат однієї операції, так і записується.

Вивчення пов'язаних із цим явищем проблем стало напрямком у математиці під назвою теорія комплексної змінної, що має велике практичне значенняу математичній фізиці.

Цікаво, що позначення кореня - радикал - застосував у своїй «Універсальній арифметиці» той самий всюдисущий І. Ньютон, а точності сучасний виглядзаписи кореня відомий з 1690 року з книги француза Роля «Керівництво алгебри».

На сьогоднішньому уроці нам необхідно запровадити поняття арифметичного квадратного кореня. Щоб це зробити, уявімо, що нам виділили ділянку землі квадратної форми (рис. 1) і хочемо виміряти довжину його боку. При цьому відомо, що сторона сітки дорівнює 1 км.

Рис. 1.

Щоб знайти довжину сторони ділянки, можна виписати теорему Піфагора прямокутного трикутника, зображеного на малюнку червоним кольором. Катети цього трикутника мають довжини по 1 км, а довжину гіпотенузи позначимо за .

Але ми поки що не знайдено сторону ділянки, а знайдено значення її квадрата.

Інакше можна було знайти так: записати площу квадратної ділянки , з іншого боку, вона дорівнює сумі площ чотирьох рівних прямокутних трикутників, з яких складається ділянка: . Але площа прямокутного трикутника, який є рівнобедреним у цьому випадку, дорівнює . Отже, площа ділянки: , і з іншого боку , т. е. отримуємо те, що було раніше: .

Питання у тому, як знайти значення сторони квадрата, т. е. ? Спробуємо перебрати числа, які можуть на роль відповіді. Почнемо з нуля, але не підходить, потім перевіримо: теж не підходить (менше двох), перевіримо: не підходить, тому що це більше двох. Отримуємо наступний висновок, що це кілька між 1 і 2, але може бути, зрозуміло, цілим. Перевіряти негативні числа не будемо, тому їх зведення в квадрат дає позитивні значення, які ми вже перевірили. Оскільки у рівняння немає цілих рішень, необхідно перевірити наявність раціональних рішень. Згадаймо для цього визначення раціонального числа.

Визначення.Раціональне число- Число, яке можна представити у вигляді дробу, в якому чисельник () є цілим числом, а знаменник () натуральним.

У вставці зазначено підтвердження того факту, що число не може бути раціональним числом.

Вставка 1. Доказ того, що не є раціональним числом

Теорема. Число , яке відповідає рівнянню , перестав бути раціональним.

Доведення. Припустимо, що число , яке задовольняє рівняння , є раціональним, тобто за визначенням раціонального числа його можна у вигляді дробу (ціле число, натуральне), причому приймемо той факт, що цей дрібнескоротна (а якщо вона скоротлива, то скоротивши її, приступимо до доказу). Підставимо такий запис до досліджуваного рівняння:

Оскільки права частина рівняння є парною, тому що має множник 2, то і ліва частина теж має бути парною. Оскільки парне, те й теж парне, т. до. воно ціле за припущенням і може бути непарним, оскільки квадрат непарного числа теж непарне число. Тоді число можна у вигляді , де - якесь ціле число. Підставимо це в отримане рівняння:

Провівши аналогічні міркування, як й у числа , можемо дійти невтішного висновку, що число є парним, та її можна як . Тоді дріб, як видно, є скоротливим, що суперечить припущенню доказу. Оскільки ми дійшли суперечності, то число не є раціональним.

Доведено.

Доведено, що число, що шукається, не може бути ні цілим, ні раціональним. Оскільки ми вперше зіткнулися з числом, яке не є цілим і не є раціональним, необхідно ввести поняття нового виду чисел. Допоможе нам у цьому поняття квадратного кореня.

Визначення.Квадратним коренем (арифметичним квадратним коренем)з неотрицательного числа називається таке неотрицательное число, квадрат якого дорівнює .

Варто відзначити важливі характеристики чисел із визначення. По-перше, квадратний корінь можна обчислювати тільки з невід'ємного числа, тобто квадратний корінь, наприклад, не має сенсу, по-друге, значення самого квадратного кореня також є невід'ємним, тобто квадратний корінь не може дорівнювати, наприклад , .

Позначенняквадратного кореняу складі : .

Відповідно ми тепер маємо можливість визначити значення сторони нашої земельної ділянки. Оскільки , то це таке число, квадрат якого дорівнює двом, а за визначенням квадратного кореня слідує, що . Таким чином, шукана сторона земельної ділянки дорівнює км.

Розглянемо приклади на роботу з квадратним корінням.

приклад 1.Чи існують вирази: , , , ?

Рішення.Для відповіді на поставлене питання необхідно скористатися визначенням, за визначенням квадратний корінь витягується лише з негативного числа. Оскільки 3, 5 і 0 є невід'ємними числами, то вирази і існують. є негативним числомтому не існує.

Відповідь., та існують; не існує.

Слід зазначити, що є випадки, коли значення квадратного кореня можна обчислити як цілого числа, а є - коли не можна. Наприклад, не можна стверджувати, що є цілим числом, і значення цього виразу так і доводиться залишати у формі кореня, а ось деякі квадратні корені можна цілими числами, переконаємося в цьому на прикладі.

приклад 2.Обчислити: а); б); в); г)

Рішення.а), тому що корінь з 4 - це таке число, квадрат якого дорівнює 4, а це 2 (). Можна стверджувати, що не враховано, що і теж має бути коренем з 4, але за визначенням квадратний корінь може бути негативним числом, тому не підходить.

б), тому що за аналогічними міркуваннями.

г) Оскільки число, з якого необхідно витягти квадратний корінь, є великим (тризначним), описаний раніше метод підбору числа, квадрат якого дорівнює 324, не зовсім зручний. Хоча хтось може знати, що в цьому випадку підходить число 18, т.к. Для спрощення пошуку відповіді розкладемо число 324 на множники: тепер спробуємо представити отримані числа у вигляді квадратів: .

Відповідь. 2; 5; 0; 18.

У ході розбирання рішення пункту «г» попереднього прикладу може виникнути питання, а на якій підставі ми маємо право стверджувати, що корінь із твору дорівнює творукоріння, адже жодні з властивостей коріння ще не введені. У наступній вставці можна ознайомитися з основними властивостями коріння, яке пояснить наші дії у вказаному прикладі.

Вставка 2. Основні властивості квадратного коріння

1. , Корінь з добутку дорівнює добутку коренів, при цьому невід'ємні;

2. , корінь із частки дорівнює приватному коренів, причому неотрицательное, позитивне;