Квадратний корінь з 2. Властивості квадратного кореня з двох

1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099 9358314132 2266592750 5592755799 9505011527 8206057147 0109559971 6059702745 3459686201 4728517418 6408891986 0955232923 0484308714 3214508397 6260362799 5251407989 6872533965 4633180882 9640620615 2583523950 5474575028 7759961729 8355752203 3753185701 1354374603 4084988471 6038689997 0699004815 0305440277 9031645424 7823068492 9369186215 8057846311 1596668713 0130156185 6898723723 5288509264 8612494977 1542183342 0428568606 0146824720 7714358548 7415565706 9677653720 2264854470 1585880162 0758474922 6572260020 8558446652 1458398893 9443709265 9180031138 8246468157 0826301005 9485870400 3186480342 1948972782 9064104507 2636881313 7398552561 1732204024 5091227700 2269411275 7362728049 5738108967 5040183698 6836845072 5799364729 0607629969 4138047565 4823728997 1803268024 7442062926 9124859052 1810044598 4215059112 0249441341 7285314781 0580360337 1077309182 8693147101 7111168391 6581726889 4197587165 8215212822 9518488472

Тож це наша мета, але, заради нашого доказу, допустимо протилежне. Припустимо, що квадратний корінь з 2 раціональних. І тоді ми побачимо, чи приведе до суперечності, що насправді цього не може бути. І якщо це не так, то це раціонально, якщо ми отримаємо протиріччя, вважаючи, що квадратний корінь з 2 раціональний, тоді ми повинні зробити висновок, що квадратний корінь з 2 має бути ірраціональним. І ми також можемо припустити, що вони не мають спільних факторів. Скажімо, що вони мали деякі загальні чинники.

Якби ми розділили чисельник і знаменник на ті самі фактори, тоді ви потрапляєте в ситуацію, коли вони не мають спільних факторів. Або інший спосіб сказати, що ми можемо написати це як відношення двох цілих чисел, де це не наводиться, де вони більше не поділяють будь-яких факторів. Якщо ви можете написати щось як відношення двох цілих чисел, то ви, очевидно, могли б спростити його далі, відняти якісь загальні фактори, щоб довести його до точки, де вона неприведена. Дозвольте мені написати це, тому що це важливо для цього доказу.

Хорошим і часто використовуваним наближенням до Неможливо розібрати вираз (виконуваний файл texvc є дріб Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \tfrac(99)(70). Незважаючи на те, що чисельник і знаменник дробу лише двоцифрові цілі, воно відрізняється від реального значення менше, ніж на 1/10000.

Ну, спробуємо трохи маніпулювати цим. Отже, все, що відбувається 2 – це буде ціле число. Ну, це має дати вам парне число, яке має дати вам парне ціле. Так що це прямо тут, квадрат, має бути. так що це говорить нам, що квадрат має бути парним. Ну, квадрат - це добуток двох числа чи є продуктом однієї й тієї числа.

Властивості квадратного кореня з двох

Так що це ще один спосіб сказати, що час, коли він дорівнює. Отже, що це говорить нам? Ми просто повинні нагадати собі, чи помножимо парні парні парні числа, отримаємо парне число. ми множимо непарне час на непарне, отримуємо непарне число, тому ми маємо число разів сам. Ну, єдиний спосіб отримати це, якщо це число парне. Отже, де все це відбувається? Тож давайте трохи подумаємо про це. Повернімося до цього кроку прямо тут. Якщо ми скажемо, що може бути представлено вдвічі як твір деякого цілого числа, і це випливає речей, а парно.

Історія

Вавилонська глиняна табличка (бл. 1800-1600 до н. е.) дає найбільш точне наближене значення Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2)при записі в чотирьох шістдесяткових цифрах, що після округлення становить 6 точних десяткових цифр:

Ви берете будь-яке ціле число 2 ви отримаєте рівну вартість. Це просто для того, щоби дати зрозуміти. Тому ви не можете зробити це. Квадратний корінь із 2 повинен бути ірраціональним. Це говорить про те, що "4 квадрати дорівнює 16". Ми також можемо квадратувати негативні числа.

Коли квадратично від'ємне число, ми отримуємо позитивний результат. Так само, як зведення в квадрат позитивного числа. Квадратний корінь йде в інший бік. Значення, яке можна помножити він, щоб вказати вихідне число. Що ми можемо помножити на себе, щоб це отримати?

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): 1 + \frac(24)(60) + \frac(51)(60^2) + \frac(10)(60^3) = 1.41421\overline(296 ).

Інше раннє наближення цього числа в давньоіндійському математичному тексті, Шульба-сутри (бл. 800-200 до н. Е..) Дається таким чином:

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): 1 + \frac(1)(3) + \frac(1)(3 \cdot 4) - \frac(1)(3 \cdot4 \cdot 34) = \ frac(577)(408) \approx 1.414215686.

Алгоритми обчислення

Існує безліч алгоритмів для обчислення значення квадратного кореняз двох. В результаті алгоритму виходить приблизне значення Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2)у вигляді звичайного або десяткового дробу. Найпопулярніший алгоритм для цього, який використовується в багатьох комп'ютерах та калькуляторах, це вавилонський метод обчислення квадратного коріння. Він полягає в наступному:

Ось ще кілька квадратів і квадратних коренів. Він також працює для десяткових чисел. Спробуйте повзунки внизу. Примітка: цифри тут показані лише на 2 десяткові знаки. Використання слайдерів. Що таке шість квадратів?

Що таке квадратний корінь із 8?
Що таке квадратний корінь із 9?
Що таке квадратний корінь із 10?
Що таке квадрат?

Раніше ми виявили, що можемо квадратувати негативні числа.

приклад. Які квадратні корені з 25?

Таким чином, квадратний корінь з 9 може бути -3 або 3. Таким чином, квадратне коріння з 25 становлять -5 і 5. І ми говоримо, що «квадратний корінь з 9 дорівнює 3». Ну, ми просто знаємо, що 25 = 5 × 5, тому коли ми помножимо 5 самі по собі, ми отримаємо.

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; math/README - довідку з налаштування.): a_(n+1) = \frac(a_n + \frac(2)(a_n))(2)=\frac(a_n)(2)+\frac(1 )(a_n).

Чим більше повторень в алгоритмі (тобто чим більше «n»), тим краще наближення квадратного кореня з двох. Кожне повторення приблизно подвоює кількість правильних цифр. Наведемо кілька перших наближень, починаючи з Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): a_0 = 1 :

Чи не може бути квадратний корінь -5? Ну квадратний корінь з 25 може бути -5 або Але коли ми використовуємо √, ми даємо тільки позитивний результат. Відповідь: 6×6 = 36, тому √36 = 6. Ідеальні квадрати – це квадрати цілих чисел. Спробуйте запам'ятати їх до.

Легко виробити квадратний корінь з ідеального квадрата, але дуже складно виробити інші квадратні корені.

Спробуємо 5: 5×5 = 25.
Спробуємо 2: 2×2 = 24.
Спробуємо 1: 1×1 = 61.

Як ви знаходите 2 рази квадратний корінь із 2 без калькулятора? Цей урок покаже вам, як робити саме це, використовуючи процес ітерації чи освічені вгадування.

3/2 = 1 .5
17/12 = 1.41 6…
577/408 = 1.41421 5…
665857/470832 = 1.41421356237 46…

Мнемонічне правило

Для запам'ятовування значення кореня з двійки з вісьма знаками після коми (1,41421356) можна скористатися наступним текстом (число літер у кожному слові відповідає десятковій цифрі): «І плід у мене, але вони мають багато коренів».

Стефані працює над шкільною грою як складовоюдизайну та реквізиту. Для одного з її проектів вона має намір розрізати квадратний шматок фанери по діагоналі навпіл. Як тільки це буде зроблено, вона зробить рамку для кожного трикутника, а потім намалює один трикутник червоний, а інший синій.

Стефані знає, що ноги трикутника будуть довжиною у два фути, тому що шматок фанери, який вона збирається відрізати, вимірюється на два фути на два фути. Вона знає, що діагоналі будуть довшими, але вона точно не знає, скільки вона не мала, щоб виміряти діагональ дошки, і в неї також не було калькулятора. Вона пам'ятає з геометрії клас, що довжина найдовшої сторони правого трикутника буде довжиною більш короткої сторони, помноженої на квадратний корінь із двох. Як вона може обчислити 2 рази квадратний корінь із 2?

Властивості квадратного кореня з двох

Половина Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2)приблизно дорівнює 0,70710 67811 86548; ця величина дає в геометрії та тригонометрії координати одиничного вектора, що утворює кут 45° з координатними осями:

Але як вона вважає, що десятковий еквівалент квадратного кореня з двох без використання Калькулятор? Один із способів зробити це – це процес повторних освічених припущень. Цей процес називається ітерацією та передбачає використання результатів останнього припущення для інформування наступного. Таким чином, ви можете наблизитися до фактичної відповіді, поки не вирішите, що знаходитесь досить близько. Перше питання – з чого почати?

Отже, давайте подивимося, що ми знаємо про квадрати чисел навколо. Квадратний корінь з 1 дорівнює 1, тому квадратний корінь з 2 має бути більшим. Крім того, квадратний корінь з 4 дорівнює 2, тому квадратний корінь з 2 має бути меншим, ніж, іншими словами, квадратний корінь з 2 знаходиться десь між 1 і нехай розділити різницю і спробувати 5 як наше перше припущення.

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \frac(\sqrt(2))(2) = \sqrt(\frac(1)(2)) = \frac(1)(\sqrt(2)) = \cos(45^\circ) = \sin(45^\circ).

Одна з цікавих властивостей Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2)полягає в наступному:

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \ (1 \over (\sqrt(2) - 1)) = \sqrt(2) + 1. Тому що Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): (\sqrt(2)+1)(\sqrt(2)-1)=2-1=1.

Це є результатом якості срібного перерізу.

Непогано, ми трохи надто високо там, тому давайте зробимо наступне припущення. Насправді це може бути точним для багатьох ситуацій, коли ми використовуємо квадратний корінь з 2, але Стефані дійсно хоче, щоб цей кадр був точним і хотів би, щоб її оцінка квадратного кореня з 2 була з точністю до двох знаків після коми.

Тепер ми стаємо дуже близькими. Це може бути не більш точним, ніж 42, і в цьому випадку ми залишимо 42 як нашу відповідь. Ми вважатимемо, що наша відповідь буде точною до двох знаків після коми. Отже, відповідь, яку ми отримуємо, становить 82 фути.

Інша цікава властивість Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2) :

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2+\sqrt(2+\sqrt(2 + \cdots))) = 2.

Квадратний корінь із двох може бути виражений у уявних одиницях iвикористовуючи тільки квадратне коріння та арифметичні операції:

Тепер, коли ми отримали відповідь, дуже хороша ідея запитати себе, чи має наша відповідь сенс. Отже, чи має сенс, що у 2 рази квадратний корінь із 2 дорівнює 82? І відповідь – так, це здається розумною відповіддю. Звичайно, це не означає, що ми маємо правильну відповідь, але ми запитуємо себе, що це питання допоможе нам уникнути великих помилок.

Одним із хороших способівперевірити вашу роботу з математичними завданнями є вирішення проблеми у зворотному напрямку. Іноді ви можете багато чого навчитися зі старого шматка глини. Вони взяли цю довжину, помножили її на квадратний корінь із 2 і отримали довжину діагоналі. І наше питання: що вони дійсно знали про квадратне коріння з 2?

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \frac(\sqrt(i)+i \sqrt(i))(i)і Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \frac(\sqrt(-i)-i \sqrt(-i))(-i).

Квадратний корінь з 2 є одниною, відмінним від 1, чия нескінченна тетрація дорівнює його квадрату.

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \sqrt(2)^ (\sqrt(2)^ (\sqrt(2)^ (\ \cdot^ (\cdot^ \cdot)))) = 2 Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): 2^m\sqrt(2-\sqrt(2+\sqrt(2+\cdots+\sqrt(2)))) \to \pi\text( as )m \to \infty

Доказ ірраціональності

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; math/README - довідку з налаштування.): \sqrt(2) = 1 + \cfrac(1)(2 + \cfrac(1)(2 + \cfrac(1)(2 + \cfrac(1) (2+\ddots)))).

Відповідні дроби даного безперервного дробу дають наближені значення, що швидко сходяться до точного квадратного кореня з двох. Спосіб їх обчислення простий: якщо позначити попередній підхідний дріб Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Math/README - довідку з налаштування.): \frac (m)(n), то наступна має вигляд Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \frac (m+2 n)(m+n). Швидкість збіжності тут менша, ніж у методу Ньютона, але обчислення набагато простіше. Випишемо кілька перших наближень:

Такі питання складні. Але оскільки вони не вигадали нічого, як «десяткову точку», вони написали це як точніше, вони написали це як це. Але ця пігулка, мабуть, була написана новачком, оскільки написано велике. Як тільки ви починаєте турбуватися про ці речі, немає кінця цьому. Одна з причин у тому, що їм справді подобаються відповідачі. Згідно з книгою Йоррана Фріберга, є таблетки, в яких вчитель поставив якогось нещасного учня завдання звернути деякі воістину гігантські цифри, такі як 325.

Вони навіть перевірили свої відповіді очевидним чином: взявши зворотну реакцію у відповідь! Вони зібрали таблиці взаємності та використали їх для вирішення більш загальних проблем поділу. Щоб розрахувати, вони розкладаються на фактори, дивляться взаємність кожного та беруть продукт разом із ним. Це круто, тому що сучасна алгебра також бачить взаємності як логічно попереднє поділ, навіть якщо більшість нематематиків не згодні!

Неможливо розібрати вираз (виконуваний файл texvcНЕ знайдений; Див. math/README - довідку з налаштування.): \frac (3)(2); frac (7)(5); frac (17)(12); frac (41)(29); frac (99)(70); frac (239)(169); frac (577)(408); frac (1393)(985); \ frac (3363)(2378) \dotsпосилань на джерела інформації.

Інформація повинна бути перевіряється, інакше вона може бути поставлена під сумнів та видалена.
.php?title=%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D1%8B%D0%B9_%D0%BA% редагувати] цю статтю, додавши посилання на .
Ця позначка встановлена 4 липня 2014 року.

На цьому планшеті вони використали значення. Але як вони одержали це наближення? Чи знають вони, що це наближення? І чи знали вони, що вони ірраціональні? Здається, немає жодних доказів того, що вони знали про ірраціональних числах. Один із великих експертів з вавілонської математики Отто Неугебауер писав.

Але є свідчення того, що вавилоняни знали, що їхня постать - лише наближення. У своїй книзі «Хрест Павла» Джордж Гевергезе Джозеф вказує, що число, схоже на це, з'являється на четвертому етапі досить очевидного рекурсивного алгоритму для апроксимації квадратного коріння! Перші три наближення.

[[К:Вікіпедія:Статті без джерел (країна: Помилка Lua: callParserFunction: функція "#property" була недоступна. )]][[К:Вікіпедія:Статті без джерел (країна: Помилка Lua: callParserFunction: функція "#property" була недоступна. )]]

Уривок, що характеризує Квадратний корінь з 2

– А я й не забула, люба. Я просто зрозуміла і прийняла її... Інакше неможливо було б існувати далі – сумно похитавши головою, відповіла дівчина.
- Як же можна зрозуміти таке? Та й що розуміти в болю?.. – не здавалася я. – Це що – мало навчити вас чогось особливого?.. Вибачте, але я ніколи не вірила в таке «вчення»! По-моєму, так лише безпорадні «вчителі» можуть використовувати біль!
Я кипіла від обурення, не в змозі зупинити свої думки, що розбігалися!.. І як не намагалася, ніяк не могла заспокоїтися.
Щиро шкодуючи дівчину-відьму, я водночас дико хотіла все про неї знати, що означало – ставити їй безліч запитань про те, що могло завдати їй болю. Це нагадувало крокодила, який, пожираючи свою нещасну жертву, лив по ній горючі сльози... Але як би мені не було соромно – я нічого не могла з собою вдіяти... Це був перший раз у моєму короткому житті, коли я майже що не звертала уваги на те, що своїми питаннями можу зробити людині боляче... Мені було дуже за це соромно, але я також розуміла, що поговорити з нею про все це чомусь дуже важливо для мене, і продовжувала запитувати, «закривши на все очі»... Але, на моє велике щастя і здивування, дівчина-відьма, зовсім не ображаючись, і далі спокійно продовжувала відповідати на мої наївні дитячі питання, не висловлюючи при цьому жодного невдоволення.
- Я зрозуміла причину того, що сталося. І ще те, що це також мабуть було моїм випробуванням... Пройшовши яке, мені відкрився цей дивовижний світ, в якому ми зараз із дідусем разом живемо. Та й багато іншого...
— Невже треба було терпіти таке, аби потрапити сюди?!. – жахнулася Стелла.
- Думаю так. Хоча я не можу сказати напевно. У кожного своя дорога... – сумно промовила Ганна. - Але головне те, що я все ж таки це пройшла, зумівши не зламатися. Моя душа залишилася чистою і доброю, не розлютившись на світ, і на людей, що мене стратили. Я зрозуміла, чому вони знищували нас... тих, що були «іншими». Яких вони називали Ведунами та Відьмами. А іноді ще й «бісовими дітьми»... Вони просто боялися нас... Боялися того, що ми сильніші за них, і також того, що ми були їм незрозумілі. Вони ненавиділи нас через те, що ми вміли. За наш Дар. І ще – надто сильно заздрили нам... І дуже мало хто знав, що багато наших вбивць, самі ж, потай намагалися вчитися всьому тому, що вміли ми, тільки от не виходило в них нічого. Душі, мабуть, надто чорними були...
– Як це – вчилися?! Але хіба вони самі не проклинали вас?.. Хіба не тому спалювали, що вважали творами Диявола? – повністю засмутивши, запитала я.
– Так воно й було, – кивнула Ганна. - Тільки спершу наші кати по-звірячому катували нас, намагаючись дізнатися заборонене, тільки нам одним ведене... А потім уже спалювали, вирвавши при цьому багатьом мови, щоб вони ненароком не розголосили творене з ними. Та ви у мами запитаєте, вона багато пройшла, більше за інших, напевно... Тому й пішла далеко після смерті, на свій вибір, чого жоден з нас не зміг.
– А де ж тепер твоя мати? - Запитала Стелла.
- О, вона десь у "чужих" світах живе, я ніколи не зможу піти туди! - З дивною гордістю в голосі, прошепотіла Ганна. - Але ми іноді кличемо її, і, вона приходить до нас. Вона любить і пам'ятає нас ... - І раптом, сонячно усміхнувшись, додала: - І такі чудеса розповідає! Як хотілося б побачити все це!
- А хіба вона не може допомогти тобі, щоб піти туди? - Здивувалася Стелла.
- Думаю - ні... - засмутилася Ганна. – Вона була набагато сильнішою за всіх нас на Землі, та й її «випробування» набагато страшніше за моє було, тому, напевно, і заслужила більше. Ну і талановитіша вона набагато була, звичайно ж...
– Але навіщо ж було потрібне таке страшне випробування? - Обережно запитала я. – Чому ваша Доля була такою Злою? Адже ви не були поганими, ви допомагали іншим, хто не мав такого Дарунка. Навіщо було творити з вами таке?!
– Для того, щоб наша душа зміцніла, я гадаю... Щоб витримати багато могли і не ламалися. Хоча тих, що зламалися, теж багато було... Вони проклинали свій Дар. І перед тим, як помирали – зрікалися його...
- Як же таке можна? Хіба можна від себе зректися?! – одразу ж обурено підстрибнула Стелла.
- Ще як можна, люба... Ох, ще як можна! - Тихо сказав, що до цього лише спостерігав за нами, але не втручався в розмову, дивовижний старець.
– Ось і дідусь вам підтвердив, – усміхнулася дівчина. – Не всі ми готові до такого випробування... Та не всі можуть переносити такий біль. Але справа навіть не стільки в болі, скільки в силі нашого людського духу... Адже після болю залишався ще страх від пережитого, який, навіть після смерті, чіпко сидів у нашій пам'яті і як черв'як, гриз крихти нашої мужності. Саме цей страх, здебільшого, і ламав людей, які пройшли весь цей жах. Варто після, вже в цьому (посмертному) світі, їх тільки трохи налякати, як вони тут же здавалися, стаючи слухняними «ляльками» в чужих руках. А вже руки ці, природно, були далеко не «білими»... Ось і з'являлися потім на Землі «чорні» маги, «чорні» чаклуни та різні подібні до них, коли їхні сутності знову поверталися туди. Маги «на мотузках», як ми називали їх... Так що, недаремно ми таке випробування проходили. Дідусь ось теж все це пройшов... Але він дуже сильний. Набагато сильніший за мене. Він зумів «піти», не чекаючи кінця. Як і мати зуміла. Тільки ось я не змогла...
- Як - піти?! Померти до того, як його спалили?! А хіба можливе таке? - У шоці запитала я.
Дівчина кивнула.
- Але не кожен це може, звичайно. Потрібна дуже велика мужність, щоб наважитися перервати своє життя... Мені не вистачило... Але дідусеві цього не позичати! – гордо усміхнулася Ганна.
Я бачила, як сильно вона любила свого доброго, мудрого діда... І на якусь коротеньку мить у моїй душі стало дуже порожнім і сумним. Ніби знову в неї повернулася глибока, невиліковна туга.
– У мене теж був дуже незвичайний дідусь… – раптом дуже тихо прошепотіла я.
Але гіркота відразу знайомо стиснула горло, і продовжити я вже не змогла.
- Ти дуже його кохала? – співчутливо запитала дівчина.
Я тільки кивнула у відповідь, усередині обурюючись на себе за таку «непрощенну» слабкість.
- Ким був твій дід, дівчинко? – лагідно спитав старець. - Я не бачу його.
- Я не знаю, ким він був... І ніколи не знала. Але, гадаю, що не бачите ви його тому, що після смерті він перейшов жити в мене... І, напевно, саме тому я й можу робити те, що роблю... Хоча можу, звичайно, ще дуже мало. ..
- Ні, дівчино, він лише допоміг тобі «відкритися». А робиш усе ти і твоя сутність. У тебе великий Дар, люба.
– Чого ж вартий цей Дар, якщо я не знаю про нього майже нічого?! - Гірко вигукнула я. – Якщо не змогла навіть урятувати сьогодні своїх друзів?!.
Я засмучено плюхнулась на пухнасте сидіння, навіть не помічаючи його «іскристої» краси, вся сама на себе ображена за свою безпорадність, і раптом відчула, як по-зрадницькому заблищали очі... А ось уже плакати в присутності цих дивовижних, мужніх людей мені ні за що не хотілося!.. Тому щоб хоч якось зосередитися, я почала подумки «перемелювати» крупинки несподівано отриманої інформації, щоб, знову ж таки, сховати їх дбайливо у своїй пам'яті, не втративши при цьому жодного важливого слова, не проґавивши якусь розумну думку...
– Як загинули ваші друзі? - Запитала дівчина-відьма.
Стелла показала картинку.
– Вони могли й не загинути… – сумно похитав головою старець. – У цьому не було потреби.
– Як це – не було?!. - Тут же обурено підскочила скуйовджена Стелла. - Вони ж рятували інших добрих людей! Вони не мали вибору!
- Вибач мені, мала, але ВИБІР Є ЗАВЖДИ. Важливо тільки вміти правильно вибрати... Ось поглянь - і старець показав те, що хвилину тому показувала йому Стелла.
- Твій друг-воїн намагався боротися зі злом тут так само, як і він боровся з ним на Землі. Але це вже інше життя, і закони в ньому зовсім інші. Так само, як інша і зброя... Тільки ви вдвох робили це правильно. А ваші друзі помилились. Вони могли б ще довго жити... Звичайно ж, кожна людина має право вільного вибору, і кожна має право вирішувати, як їй використовувати її життя. Але це, коли він знає, як міг би діяти, знає всі можливі шляхи. А ваші друзі не знали. Тому – вони і припустилися помилки, і заплатили найдорожчою ціною. Але в них були прекрасні і чисті душі, тому пишайтеся ними. Тільки ось уже ніхто і ніколи не зможе їх повернути.

Квадратний корінь із числа 3- Позитивне дійсне число, яке при множенні саме він дає число .

Але якщо ви працюєте в 3-х місцях на базі 60, як це роблять вавилоняни, ви отримаєте номер на цьому планшеті! Таким чином, індійські математики, можливо, знали той самий алгоритм. Але що це за алгоритм? Джозеф описує це, але Шрідхар Рамеш розповів нам про легший спосіб думати про це. Припустимо, ви намагаєтеся вирахувати квадратний корінь з 2, і у вас є припущення, скажімо. Якщо ви здогадуєтеся точно.

Але якщо ваша здогад неправильна, вона не буде повністю рівна. Тому має сенс прийняти середнє значення і використовувати це як нове припущення. Насправді він сходить дуже швидко: на кожному кроці кількість правильних цифр у вашій здогаді приблизно подвоїться! Почнемо з очевидної дурної припущення, зокрема.

Його приблизним значенням із 69 цифрами після коми є:

Округлене значення 1.732 правильне з точністю до 0,01 %. Приблизною правильним дробомє ( 1,732 1 42857…).

Хорошим і часто використовуваним наближенням є дріб. Незважаючи на те, що чисельник і знаменник дробу лише двоцифрові цілі, воно відрізняється від реального значення менше, ніж на 1/10000.

Ми робимо розрахунок у копіткій деталі з двох причин. По-перше, ми хочемо довести, що ми так само хороші в арифметиці, як давні вавилоняни: нам не потрібен калькулятор для цього! По-друге, милий малюнок з'явиться, якщо ви звернете увагу. Ви пам'ятаєте, що таке 17 разів 17? Ви пам'ятаєте, що таке 12 разів 24? Ну, можливо, ви пам'ятаєте, що 12 разів 12. Отже, рухаючись прямо, ми отримуємо.

Які, мабуть, використали вавилоняни! Навіть якщо ви це зробите, добре спробувати інший раунд цієї гри, щоб побачити, чи ця картина зберігається. Крім того, буде весело бити вавилонян у своїй грі та отримати найкраще наближення. Ви пам'ятаєте, що таке 577 разів 577? Фактично зараз калькулятор починає виглядати дуже добре. Добре: у ньому йдеться, що відповідь 332. І це той шаблон, на який ми натякали: він працював так щоразу.

Система зчислення	Оцінка числа √2
Ірраціональні числа - ζ(3) - √2 - √3 - √5 - - - - -

Двійкова	1.0110101000001001111…
Десяткова	1.4142135623730950488…
Шістнадцяткова	1.6A09E667F3BCC908B2F…
Безперервний дріб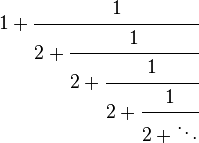

Історія

Вавилонська глиняна табличка із примітками.

Вавилонська глиняна табличка (бл. 1800-1600 до н. е.) дає наближене значення у чотирьох шістдесяткових цифрах, що становить 8 десяткових цифр:

Алгоритми обчислення

Існує безліч алгоритмів для обчислення значення квадратного кореня із двох. В результаті алгоритму виходить приблизне значення у вигляді звичайного або десяткового дробу. Найпопулярніший алгоритм для цього, який використовується в багатьох комп'ютерах та калькуляторах, це вавилонський метод обчислення квадратного коріння. Він полягає в наступному:

3/2 = 1 .5
17/12 = 1.41 6…
577/408 = 1.41421 5…
665857/470832 = 1.41421356237 46…

Інша цікава властивість √2:

Квадратний корінь з 2 є одниною, відмінним від 1, чия нескінченна тетрація дорівнює його квадрату.

Доказ ірраціональності

Застосуємо доказ від неприємного: припустимо, раціональний, тобто представляється у вигляді нескоротного дробу, де і - цілі числа. Зведемо передбачувану рівність у квадрат:

Звідси випливає, що парно, отже, парно і . Нехай де ціле. Тоді

Отже, парно, отже, парно і . Ми отримали, як і парні, що суперечить нескоротності дробу . Отже, вихідне припущення було неправильним, і – ірраціональне число.

Безперервний дріб

Квадратний корінь із двох може бути представлений у вигляді