Безліч дійсних чисел відрізка 0 1 незліченна. Числові множини
>>Математика:Багато дійсних чисел
Безліч дійсних чисел
а + b = b + а;
a + (b + c) = (a + b) + c
(а + b) с = ас + bc і т.д.
Виконуються і звичні правила: твір (приватний) двох позитивних чисел - додатне число;
добуток (приватний) двох негативних чисел - позитивне число; твір (приватний) позитивного та - від'ємне число.
Дійсні числа можна порівнювати один з одним, використовуючи таке визначення.
Визначення
. Кажуть, що дійсне число а більше (менше) дійсного числа b, якщо їхня різниця а - b - позитивне (негативне) число. Пишуть > b (а< b).
З цього визначення випливає, що будь-яке позитивне число а більше нуля (оскільки різниця а - 0 = а - позитивне число), а всяке негативне число b менше нуля (оскільки різниця b - 0 = b - негативне число).
Отже, а > 0 означає, що - позитивне число;
а< 0 означает, что а - отрицательное число;
а>b означає, що а -b - додатне число, тобто а - b> 0;
a тобто. а - b< 0.
Поряд зі знаками суворих нерівностей (<, >) використовують знаки нестрогих нерівностей:
а 0 означає, що а більше за нуль або дорівнює нулю, тобто а - невід'ємне число (позитивне або 0), або що не менше нуля;
а 0 означає, що менше нуля або дорівнює нулю, тобто а - непозитивне число (негативне або 0), або що не більше нуля;
а b означає, що а більше абоодно b, т. е. а - b - невід'ємне число, або що менше b; а - b0;
а b означає, що а менше або дорівнює b, тобто а - b - непозитивне число, або що не більше Ь; а – b 0.
Наприклад, для будь-якого числа а правильна нерівність а 2 0;
для будь-яких чисел а і b правильна нерівність (а - b) 20.
Втім, для порівняння дійсних чисел необов'язково щоразу складати їхню різницю і з'ясовувати, позитивна вона чи негативна. Можна зробити відповідний висновок, порівнюючи записи чисел у вигляді десяткових дробів.
Геометрична модель безлічі дійсних чисел, тобто числова пряма, робить операцію порівняння чисел особливо наочною: з двох чисел а, b більше те, що розташовується на числовій прямій правіше.
Таким чином, до порівняння дійсних чисел потрібно підходити досить гнучко, що ми і використовуємо в наступному прикладі.
приклад 1.Порівняти числа:

приклад 2.Розташувати у порядку зростання числа
![]()
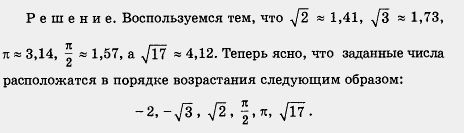
Мордкович А. Р. Алгебра. 8 кл.: Навч. для загальноосвіт. установ.- 3-тє вид., Доопрацювання. – М.: Мнемозіна, 2001. – 223 с: іл.
Планування математики, матеріали з математики 8 класу скачати , підручники онлайн
Зміст уроку конспект урокуопорний каркас презентація уроку акселеративні методи інтерактивні технології Практика завдання та вправи самоперевірка практикуми, тренінги, кейси, квести домашні завдання дискусійні питання риторичні питання від учнів Ілюстрації аудіо-, відеокліпи та мультимедіафотографії, картинки графіки, таблиці, схеми гумор, анекдоти, приколи, комікси притчі, приказки, кросворди, цитати Доповнення рефератистатті фішки для допитливих шпаргалки підручники основні та додаткові словник термінів інші Вдосконалення підручників та уроківвиправлення помилок у підручникуоновлення фрагмента у підручнику елементи новаторства на уроці заміна застарілих знань новими Тільки для вчителів ідеальні урокикалендарний план на рік методичні рекомендації програми обговорення Інтегровані урокиВихідним методом Кантора порівняння нескінченних множин було встановлення їх рівнопотужності. В основі ідеї рівноваги лежить поняття відповідності. Якщо кожен елемент однієї множини можна поставити у взаємооднозначну відповідність елементу іншої множини, то ці множини рівносильні. Відповідність ця, насправді, деяка алгоритм, який і провадить таку процедуру. Якщо нескінченна множина рівномірна безлічі натуральних чисел, то кажуть, що вона рахунково. Насправді це означає, що відомий алгоритм, який дозволяє в деякому порядку перебирати всі елементи цієї множини і цим нумерувати (ставити у відповідність натуральним числам). Іншими словами, це має бути перелічена безліч.
Те, що множини є підмножинами натурального ряду (наприклад, парні числа) є лічильними особливого подиву не викликає. Несподіваніше було те, що можна пронумерувати раціональні числа, яких явно "більше" ніж натуральні. І алгоритм тривіальний — після скорочення загальних множників необхідно перейти ґеделівському числу, тому безліч пар перелічимо. Це оборотний алгоритм і можна відновити і . Аналогічно, використовуючи більш довгий ряд простих чисел, можна пронумерувати будь-які фіксовані набори цілих чисел.
Оригінальна нумерація Кантора полягала в розташуванні раціональних чисел у вигляді таблиці та перерахування їх по діагоналях, починаючи з лівого верхнього кута: ; ; ;... так, що на кожній діагоналі дорівнює 2, 3, 4,...
Інший універсальний прийом нумерації - це лексографічне впорядкування (за довжиною, а за однакової довжини за алфавітом). Записавши раціональне число як рядки , а цілі й у 10-й системі числення ці рядки, зрозуміло, можна впорядкувати, тобто. перерахувати. З цієї причини рахунковими виявляються алгебраїчнічисла, тобто. коріння рівнянь із цілими коефіцієнтами. Частина їх (наприклад, ) раціональними є. Усі нераціональні числа ми називаємо ірраціональними.
Після встановлення рахунковини безлічі раціональних і алгебраїчних чисел, Кантор, за допомогою знаменитого діагонального міркування показав, що безліч дійсних чисел незліченна. Однак що таке дійсні числа? Один із підходів визначення їх, це звернутися до геометрії.
Розглянемо відрізок прямий, довжина якого прийнято за одиницю. Справжнє число - це відстань певної точки всередині цього відрізка від лівого краю (нуля). Як ми можемо вимірювати довжину відрізків менших за базовий? Можна за допомогою геометричних побудов (вимагають своєї аксіоматики) розбити відрізок на рівних частин (або поєднати однакових відрізків, оголосивши результат одиничним).
Якщо можна з'ясовувати, яка точка лежить ближче до нуля, то відстань виражається за допомогою нерівності:
Взявши дуже великим, можна як завгодно сильно затиснути діапазон неточності (кордону нерівності), тобто. наблизити дійсну кількість раціональними з будь-якою заданою помилкою. Хоча останні визначаються тільки парою цілих і вони всюди щільно покривають відрізок. Які б дві точки ми не взяли, неважливораціональні або ірраціональні, між ними завжди буде знаходитися скільки завгодно багато раціональних чисел. І якщо натуральні числа, відкладені на прямий, очевидно "діряві", то "між" раціональними "дірок" немає! Лапки підкреслюють психологічність цього твердження.
Другий спосіб вимірювання відстані полягає у використанні ієрархічно зменшуються "лінійок". Для цього будемо використовувати наступне кодування для "зображення" числа. Напишемо "". Потім розділимо відрізок на дві рівні частини і з'ясуємо в якій лежить точка. Якщо у лівій, то далі поставимо 0, а якщо у правій, то 1:
У разі вона справа, тому маємо " " . Праву половину знову ділимо на дві рівні частини і з'ясовуємо в якій із них знаходиться. Тепер ліворуч, тож "". Повторюючи цю процедуру, отримаємо двійкове уявленнячисла еквівалентне ряду:
Також виходить десяткове уявлення, тільки ділити необхідно щоразу на 10 рівних частин. Іноді опиняється межі розподілу, і процедура зупиняється. Виходить кінцеве уявлення у цій системі числення. У двійковій системі такі кінцеві числамають вигляд, де-непарно, а в десятковій, де не ділиться на 10. Тому кінцеве в двійковій буде звичайно і в десятковій, але, взагалі кажучи, не навпаки.
Повернемося до Георга Кантора, і розглянемо багато всіх дійсних чисел, визначених за допомогою процедури, описаної вище. Використовуватимемо двійкову систему числення. Деякі (навіть раціональні) числа у ній будуть нескінченною послідовністю нулів та одиниць (наприклад 1/3). Зручно вважати всі числа нескінченними, дописуючи праворуч до кінцевих необмежену послідовність нулів. Доведемо, що багато таких чисел не злічено.
Звичайно доказ буде будуватися за схемою "від неприємного". Нехай усі дійсні числа в інтервалі можна пронумерувати. Як би ми це не зробили, вийде певний перелік:

Іншими словами, у нас є бінарна функція (рівна 0 або 1) виду , де номер номер, а номер двійкової цифри в числі після точки. У прикладі вище. Побудуємо число, перша цифра після точки якого не дорівнює першій цифрі першого числа, друга не дорівнює другій цифрі другого числа і т.д. Іншими словами, ![]() , де введено бінарну операцію інвертування: і . У прикладі вище початок цього числа
, де введено бінарну операцію інвертування: і . У прикладі вище початок цього числа
Це новечисло не входить до нашої послідовності, оскільки воно відрізняється від першого числа першою цифрою, від другого — другою, тощо. Ми дійшли суперечності із твердженням, що всі речові числа були пронумеровані. Отже, цього не можна зробити, і множина речових чисел не злічується.
Часто, на підставі цього доказу, кажуть, що ірраціональних чисел "більше", ніж раціональні, які є рахунковими. Це не вірно.
По-перше, між будь-якими ірраціональними числами завжди розташовано безліч раціональних чисел. У двох близьких, але не рівних ірраціональних чисел перші цифри двійкового розкладання співпадуть. Ми завжди можемо вибрати раціональне число у вигляді кінцевого раціонального дробу, у якого цифр збігаються з першими цифрами числа "" і далі йдуть нулі. Вочевидь, що це раціональне число буде більше " " і менше " " . Якби ірраціональних чисел було "більше" ніж раціональних, то ми отримали б досить неприємну ситуацію: між будь-якимидвома ірраціональними числами завжди плутається нескінченна кількість раціональних, яких менше! Хоча, звичайно, це надто "психологічний" аргумент.
По-друге, досить важко відповісти на просте запитання - а які справжні числа виявилися незліченними? Безліч раціональних та алгебраїчних чисел рахункове. Тому, традиційна відповідь - незліченними є "всі інші" речові числа, а саме трансцендентні. До трансцендентних чисел, зокрема, відносяться "" та "". У такому формулюванні це твердження теж неправильне.
Як з'являються (визначаються) у математиці ті чи інші конкретнічисла? Насамперед — як розв'язання будь-яких рівнянь. Наприклад, це позначення (ім'я!) числа, що є розв'язком рівняння . Числа можна визначити за допомогою нескінченних рядів та меж. Так "", або . Незважаючи на те, що ці формули виражають деякі нескінченні дії, саме визначення числа "" - звісно. Так, крапка у визначенні низки лише означає, що ми є кінцевий алгоритм, що дозволяє отримати будь-який, наперед заданий, його член. Ще одним способом визначення числа є пред'явлення алгоритму обчислення будь-якої цифри у його десятковому поданні. Таким є трансцендентне число Ліувіля: 0.11000100000000000000010..., де-я одиниця стоїть у позиції .
У всіх цих випадках існує алгоритм чи визначення, що задає число. Визначення не обов'язково має бути конструктивним (не обов'язково є алгоритм, що обчислює це число). Наприклад, розглянемо десяткове уявлення числа . Назвемо число, яке дорівнює максимальній кількості нулів, що йдуть підряд, у десятковому записі числа (для мільйона цифр ). Якщо максимальної послідовності немає, то . Таке неконструктивне число визначено " дуже добре " , але воно визначено. Принаймні, якщо ми віримо, Що максимальна послідовність чи існує, чи ні, і третього не дано.
Якою б не була побудова конкретного числа (конструктивним чи неконструктивним),
всі визначення, всіх чисел, з якими ми маємо і будь-коли матимемо справу в математиці, задаються кінцевою послідовністю слів, що складаються з букв кінцевого алфавіту.Такі визначення і, отже, числа лічильні за тією самою причиною, за якою лічильні формули або алгоритми.
Таким чином, усі, хоч якось зумовлені речові числа, є рахунковими. Що ж тоді ми не змогли порахувати?
Математичне міркування коректно, що його логічна структура істинна незалежно від змістовного сенсу що у ньому об'єктів. Повернемося до Проблеми Зупинки і представимо такий "доказ" незліченні функцій, що обчислюються:
Розглянемо багато всіх обчислюваних функцій однієї змінної. Нехай це безліч рахунків, тобто. Кожна функція має номер: . Побудуємо функцію. Вона також визначається алгоритмом. Вона не збігається з жодною функцією . Ми дійшли суперечності. Тому безліч таких функцій незліченна.Ми знаємо, що цей "доказ" свідомо неправильний. Точніше воно доводить не численність обчислюваних функцій а неможливість побудови універсального алгоритму, який з'ясовує певність функції. Його відсутність не дозволяє визначити значення за деяких. Тому і порівняння, і іноді просто некоректне.
Не складно бачити, що структура "доказів" незліченні функцій та дійсних чисел еквівалентні. У разі функцій ми твердо знали, що їх безліч рахунків, оскільки отримали цей результат прямим, а не непрямим міркуванням. Чи рахункові речові числа ми знаємо, тому, отримавши протиріччя, з радістю робимо висновок що вони незліченні. Проте, лічильність це єдине припущення. Ми віримо, що для будь-якого числа можна отримати -ю цифру, а завдяки цьому можна побудуватичисло відмінне від інших у вже впорядкованої послідовності.
Відомо, що кожна обчислювана і всюди певна функція ставить певне матеріальне число. Такими функціями у доказі Кантора були. Можна розширити це визначення речового числа на всі можливі алгоритми. Але тоді ми отримаємо безліч "не зовсім" певних речових чисел. Найпростіший приклад такого числа є наступним. Нехай -та цифра двійкового уявлення числа дорівнює 1, якщо -тий алгоритм усюди визначений, і 0 інакше: Ми важливоне можемо запропонувати алгоритму, який завжди визначає зупинку даної програми, тому для деяких чисел, у деяких позиціях стоятиме невизначена цифра "?". Отже, ми не можемо порівняти це число з іншим дійсним числом (що намагаємося робити в доказі Кантора). Питання: чи є таким чином заданий об'єкт загалом числом? Наприклад, до нього не застосовується те, що робить число власне числом: арифметичні дії та операції порівняння.
На всіх етапах розвитку математики ставлення до числа визначали рівень значущості математичних знань. Глибоке проникнення теорію числових множин поєднувалося з містичним і наївним розумінням їх властивостей. Багато досягнень теорії чисел з'являлися як зухвалі припущення людської думки.
Уявлення про число існувало ще в давнину, але лише в XIX столітті ці знання стали формуватися в сувору наукову теорію.
Вам поклоняюся, вас бажаю, числа!
Вільні, безтільні, як тіні,
Ви веселкою сполучною повисли
До роздумів із вершини натхнення.
Валерій Брюсов
Число є сутністю всіх речей.
Ще піфагорійці у VI-V століттях до н. е. при вимірі геометричних величин зіткнулися з недостатністю раціональних чисел під час вирішення деяких завдань. З цієї причини дії проводилися над геометричними величинами, а не над числами, що їх виражають. Перші спроби введення ірраціональних чисел були в VI столітті до н.е. грецькими математиками Теететом і Евдоксом, пізніше – “Початках” Евкліда. Лише через півтора тисячоліття арабський математик і поет Омар Хайям зробив новий внесок у розуміння ірраціональності.Щоб звільнити алгебру від геометричної форми, потрібно створити загальне уявлення про числа і дії над ними, не засноване на геометрії.
Поняття дійсного числа виникло в математиці не відразу. Багато завдань теорії дійсних чисел мають дуже
Бог створив натуральний ряд, решта – справа людських рук.
Л. Кронекер
давню історію. Проблеми, що виникали щодо різних числових множин, виникали спонтанно, відособлено, визначаючи часом вирішення суміжних питань. Але глибоке розуміння цих проблем виникло, мабуть, пізніше за створення самого математичного аналізу, заснованого на теорії дійсних чисел.Потреби рахунку предметів призвели до появи множини натуральних чисел
і раціональні числа
,
де ![]()
нескоротна, у розкладаннях m і n немає спільних множників. Це дозволяє досягти однозначності запису раціональних чисел.
Введення раціональних чисел виявилося недостатнім вирішення деяких завдань. Наприклад, діагональ квадрата зі стороною, що дорівнює 1 , може бути представлена раціональним числом. З'явилися нові числа ірраціональні . Вже Аристотель намагався довести, що число ірраціональне.
Можна сміливо сказати, що раціональні числа заповнюють не всю числову пряму. Прагнення поставити у відповідність кожній точці прямий кілька призвело до появи нових чисел – ірраціональних чисел.
На рубежі XIX і XX століть Р. Дедекіндом була створена теорія ірраціональних чисел, згідно з якою за допомогою методу перерізів в області раціональних чисел кожне ірраціональне число може бути з будь-яким ступенем точності виражено через раціональні числа. Тобто будь-яке ірраціональне число може бути укладено в скільки завгодно малий інтервал, межі якого – раціональні числа.
Розглянемо число. Покажемо, що немає раціонального числа – ні цілого, ні дробового, квадрат якого дорівнює 2 .
Припустимо неприємне: «знайдеться таке раціональне число x , Що.» Очевидно, серед цілих чисел немає числа, що дорівнює, оскільки. Крім того, так як. Кожне позитивне раціональне число, не рівне 0 , можна у вигляді нескоротного дробу. Приймемо
де m і n - натуральні числа, які не мають інших спільних дільників, крім 1 . Тоді має бути вірною рівність
або . Отже, m
2
– число парне, отже m
теж парно ( m
може бути непарним, оскільки його квадрат був би також непарним). Якщо m
= 2k
, то ![]() або, тобто n
– число парне. Ми бачимо, що у нескоротного дробу і чисельник, і знаменник –
числа парні, що неможливо через нескоротність дробу, отже не є раціональний дріб.
або, тобто n
– число парне. Ми бачимо, що у нескоротного дробу і чисельник, і знаменник –
числа парні, що неможливо через нескоротність дробу, отже не є раціональний дріб.
Сукупність раціональних та ірраціональних чисел утворює безліч R –множина дійсних чисел . Їх називають ще РЕЧОВИНИМИ ЧИСЛАМИ . У математиці розглядаються різні, еквівалентні способи введення дійсних чисел. Ми визначимо їх як нескінченні десяткові дроби виду
![]() ,
,
де - деяке ціле невід'ємне число, - цифри 0, 1, 2, ... , 9 . З двох знаків ” береться лише одне: для позитивних чисел– знак “ + ”, для негативних чисел – знак “–”. Знак “ + ” зазвичай опускають.
Раціональні числа у вигляді нескінченних десяткових періодичних дробів, ірраціональні –як нескінченних неперіодичних десяткових дробів. Деякі раціональні числа є кінцевими десятковими дробами, однак вони можуть бути задані і у вигляді нескінченних десяткових дробів з нулем у періоді або у вигляді нескінченного десяткового дробу з цифрою 9 у періоді.
Наприклад, ![]() ,
,
або ![]() .
.
Дійсна кількість ![]() одно числу
одно числу ![]() водному з наступних випадків:
водному з наступних випадків:
Інакше вважають.
Порівняємо нерівні між собою числа. Тут можливі три випадки.
1. a і b - Невід'ємні. Завжди знайдеться натуральне n (або n =0 ), що і. Вважатимемо, що a b , якщо a n b n, і a b , якщо a n b n.
2. a - Негативне число, b - Негативно. Тоді рахують a b . (Прі a b крапка a на числовій осі лежить правіше точки b ).
Мистецтво аналітиків у тому, що вони, усуваючи невитончені обчислення, розробляють алгебраїчні ідеї, отже, замість споглядання простору користуються розглядом чисел.
Енциклопедія елементарної математики
(Одеса, 1914 р.)
3. Для a і b – негативних вважають, що a b , якщо | a | |b |і a b , якщо | a | |b |.Запис означає, що або.
Безліч дійсних чисел R можна зобразити точками числової прямої, на якій вибрано початок відліку O , масштаб (одиничний відрізок) та її позитивна орієнтація: точці М , що лежить праворуч від точки Про , поставимо у відповідність число c > 0 , що дорівнює довжині відрізка ОМ , точці Р , розташованої зліва від точки Про ,–число d< 0 , де | d | -довжина відрізка ВР , А точці Про - Число 0 . Приймемо без доказу, що між точками прямої та безліччю дійсних чисел існує взаємно однозначна відповідність. Ось чому безліч дійсних чисел називають числовою прямою, а самі числа – точками. Таким чином, - безліч всіх дійсних чисел (числова пряма).
Нагадаємо, тут вже відому термінологію:
– відрізок (сегмент) -Більшість всіх дійсних чисел x , що задовольняють нерівності;


