Правильний дріб завжди. Множення та розподіл. Дії над десятковими дробами

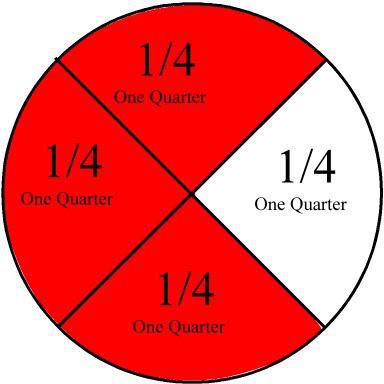
З дробами ми стикаємося у житті набагато раніше, ніж починається їхнє вивчення у школі. Якщо розрізати ціле яблуко навпіл, ми отримаємо частину фрукта - ½. Розріжемо ще раз – буде ¼. Це і є дроби. І все, начебто, просто. Для дорослої людини. Для дитини ж (а цю тему починають вивчати в кінці молодшої школи) абстрактні математичні поняття ще лякаюче незрозумілі, і викладач повинен доступно пояснити, що таке правильний дріб і неправильний, звичайний і десятковий, які операції можна з ними здійснювати і, головне, для чого все це потрібне.

Які бувають дроби

Знайомство з новою темою в школі починається з звичайних дробів. Їх легко впізнати по горизонтальній межі, що розділяє два числа – зверху та знизу. Верхнє називається чисельником, нижнє – знаменником. Існує і малий варіант написання неправильних і правильних звичайних дробів – через косу межу, наприклад: ½, 4/9, 384/183. Такий варіант використовується, коли висота рядка обмежена і немає можливості застосувати двоповерхову форму запису. Чому? Та тому що вона зручніша. Трохи згодом ми в цьому переконаємося.

Крім звичайних, існують також десяткові дроби. Розрізнити їх дуже просто: якщо в одному випадку використовується горизонтальна або похила риса, то в іншому – кома, що розділяє послідовності цифр. Подивимося приклад: 2,9; 163,34; 1,953. Ми навмисно скористалися крапкою з комою як роздільник, щоб розмежувати числа. Перше буде читатися так: «дві цілих, дев'ять десятих».

Нові поняття

Повернемося до звичайних дробів. Вони бувають двох видів.

Визначення правильного дробу звучить наступним чином: це такий дріб, чисельник якого менший за знаменник. Чому це важливо? Зараз побачимо!

У вас є кілька яблук, поділених на половинки. Усього – 5 частин. Як ви скажете: у вас «два з половиною» чи «п'ять других» яблука? Звичайно, перший варіант звучить більш природно, і при розмові з друзями ми скористаємося ним. А от якщо потрібно порахувати, скільки фруктів дістанеться кожному, якщо в компанії п'ять осіб, ми запишемо число 5/2 і розділимо його на 5 - з точки зору математики це буде наочніше.

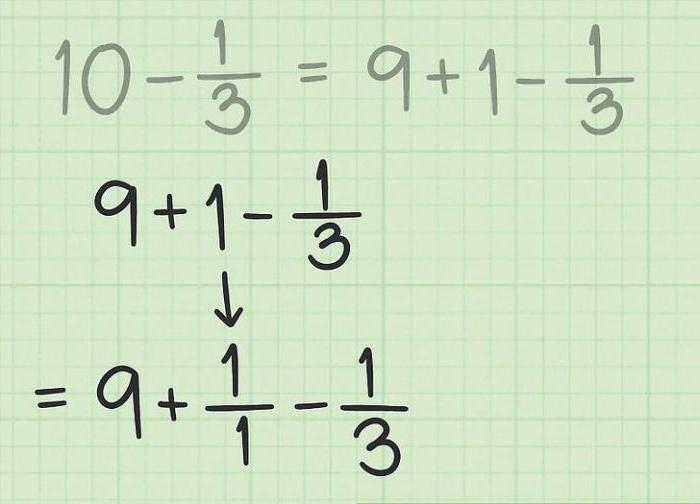Отже, для найменування правильних і неправильних дробів правило таке: якщо дробу можна виділити цілу частину (14/5, 2/1, 173/16, 3/3), вона є неправильною. Якщо цього зробити не можна, як у випадку з 13/16, 9/10, вона буде правильною.

Основна властивість дробу

Якщо чисельник і знаменник дробу одночасно помножити або розділити на те саме число, його величина не зміниться. Уявіть: торт нарізали на 4 рівні частини і дали вам одну. Такий самий торт порізали на вісім частин і дали вам дві. Чи не все одно? Адже ¼ і 2/8 - це одне й те саме!

Скорочення

Автори завдань та прикладів у підручниках з математики найчастіше прагнуть заплутати учнів, пропонуючи громіздкі у написанні дробу, які насправді можна скоротити. Ось приклад правильного дробу: 167/334, який, начебто, виглядає дуже «страшно». Але насправді ми можемо записати його як? Число 334 ділиться на 167 без залишку - зробивши таку операцію, ми отримаємо 2.

Змішані числа

Неправильний дріб можна подати у формі змішаного числа. Це коли ціла частинавинесена вперед та записана на рівні горизонтальної межі. Фактично вираз набуває вигляду суми: 11/2 = 5 + ½; 13/6 = 2 + 1/6 тощо.

Щоб винести цілу частину, потрібно розділити чисельник на знаменник. Залишок від розподілу записати зверху, над межею, а цілу частину - перед виразом. Таким чином, ми отримуємо дві структурні частини: цілі одиниці + правильний дріб.

Можна здійснити і зворотну операцію - цього потрібно цілу частину помножити на знаменник і додати отримане значення до чисельнику. Нічого складного.

Множення та розподіл

Як не дивно, множити дроби простіше, ніж складати. Усього-то і потрібно - продовжити горизонтальну межу: (2/3) * (3/5) = 2 * 3 / 3 * 5 = 2 / 5.

З поділом теж все просто: потрібно перемножити дроби навхрест: (7/8) / (14/15) = 7 * 15 / 8 * 14 = 15 / 16.

Складання дробів

Що робити, якщо потрібно здійснити додавання або в знаменнику у них різні числа? Вчинити так само, як з множенням, не вийде - тут слід розуміти визначення правильного дробу та його сутність. Потрібно привести доданки до спільному знаменнику, тобто в нижній частині обох дробів мають бути однакові числа.

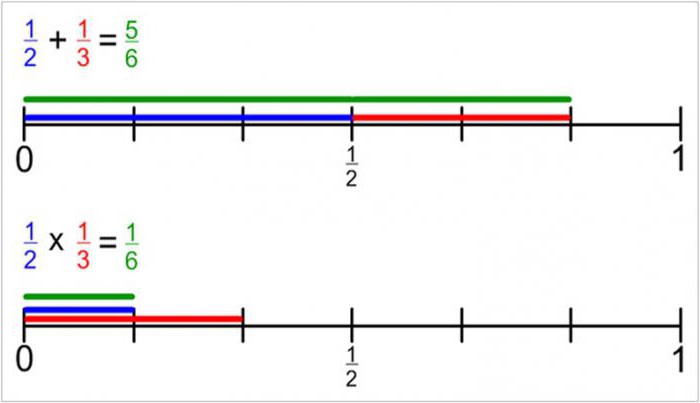Щоб це здійснити, слід скористатися основною властивістю дробу: помножити обидві частини на те саме число. Наприклад, 2/5 + 1/10 = (2 * 2) / (5 * 2) + 1 / 10 = 5 / 10 = ½.

Як вибрати, до якого знаменника приводити доданки? Це має бути мінімальне число, кратне обом числам, що стоять у знаменниках дробів: для 1/3 та 1/9 це буде 9; для ½ і 1/7 - 14, тому що меншого значення, що ділиться без залишку на 2 та 7, не існує.

Використання

Для чого потрібні неправильні дроби? Адже набагато зручніше одразу виділити цілу частину, отримати змішане число- І справа з кінцем! Виявляється, якщо потрібно виконати множення або поділ двох дробів, вигідніше скористатися саме неправильними.

Візьмемо наступний приклад: (2+3/17)/(37/68).

Здавалося б, скоротити зовсім нічого. Але що, якщо записати результат додавання у перших дужках у вигляді неправильного дробу? Подивіться: (37/17) / (37/68)

Тепер все стає на свої місця! Запишемо приклад таким чином, щоб усе стало очевидним: (37*68) / (17*37).

Скоротимо 37 у чисельнику та знаменнику і, нарешті, розділимо верхню та нижню частини на 17. Ви ж пам'ятаєте основне правило для правильного та неправильного дробу? Ми можемо множити і ділити їх на будь-яке число, якщо це робимо одночасно для чисельника і знаменника.

Отже, отримуємо відповідь: 4. Приклад виглядав складним, а відповідь містить лише одну цифру. У математиці так часто трапляється. Головне - не боятися і дотримуватися простих правил.

Поширені помилки

При здійсненні дій з дробами учень може легко зробити одну з найпопулярніших помилок. Зазвичай вони відбуваються через неуважність, а іноді через те, що вивчений матеріал ще не відклався в голові як слід.

Часто сума чисел, що стоїть у чисельнику, викликає бажання скоротити окремі її компоненти. Допустимо, у прикладі: (13 + 2) / 13, написаному без дужок (з горизонтальною межею), багато учнів з недосвідченості закреслюють 13 зверху та знизу. Але так робити не можна в жодному разі, адже це груба помилка! Якби замість додавання стояв знак множення, ми отримали б у відповіді число 2. Але при здійсненні додавання жодні операції з одним із доданків не дозволені, тільки з усією сумою цілком.

Ще хлопці часто помиляються при розподілі дробів. Візьмемо два правильні нескоротні дроби і розділимо один на одного: (5/6)/(25/33). Учень може переплутати і записати результуючий вираз як (5*25)/(6*33). Але так вийшло б при множенні, а в нашому випадку все буде трохи інакше: (5*33) / (6*25). Скорочуємо те, що можливо, та у відповіді побачимо 11/10. Неправильний дріб, що вийшов, запишемо як десятковий - 1,1.

Дужки

Пам'ятайте, що у будь-яких математичних висловлюваннях порядок дій визначається пріоритетом знаків операцій та наявністю дужок. За інших рівних відлік черговості виконання дій відбувається зліва направо. Це актуально і для дробів - вираз у чисельнику чи знаменнику розраховується строго за цим правилом.

Адже це результат розподілу одного числа на інше. Якщо вони не діляться націло, виходить дріб - ось і все.

Як записати дріб на комп'ютері

Оскільки стандартні засоби не завжди дозволяють створити дріб, що складається з двох «ярусів», учні часом йдуть на різні хитрощі. Наприклад, копіюють чисельники і знаменники в графічний редактор Пейнт і склеюють їх воєдино, малюючи між ними горизонтальну лінію. Звичайно, є простіший варіант, який, до речі, надає і масу додаткових можливостей, які стануть вам корисними в майбутньому.

Відкрийте "Майкрософт Ворд". Одна з панелей у верхній частині екрана має назву «Вставка» - натисніть її. Справа, в тому боці, де розташовані значки закриття та згортання вікна, є кнопка «Формула». Це саме те, що нам потрібне!

Якщо ви скористаєтеся цією функцією, на екрані з'явиться прямокутна область, в якій можна використовувати будь-які математичні знаки, які відсутні на клавіатурі, а також писати дроби у класичному вигляді. Тобто розділяючи чисельник і знаменник горизонтальною межею. Ви навіть можете здивуватися, що такий правильний дріб настільки легко записати.

Вивчайте математику

Якщо ви навчаєтеся в 5-6 класі, то вже скоро знання математики (у тому числі – вміння працювати з дробами!) знадобиться у багатьох шкільних предметах. Майже в будь-якому завданні з фізики, при вимірюванні маси речовин в хімії, в геометрії та тригонометрії без дробів не обійтися. Вже скоро ви навчитеся обчислювати все в умі, навіть не записуючи вирази на папері, але з'являтимуться все більше і більше складні приклади. Тому вивчіть, що таке правильний дріб і як з ним працювати, не відставайте за навчальною програмою, своєчасно робіть домашні завдання, і тоді ви досягнете успіху.

При цьому число mназивається чисельником, а число n - знаменникомдроби. Такий дріб слід інтуїтивно розуміти, як результат поділу mна nнавіть якщо націло розділити не вдається. У реальному житті можна використовувати раціональні числа для рахунку частин деяких цілих, але ділених об'єктів, наприклад, тортів або інших продуктів, що розрізаються на кілька частин перед вживанням, або для грубої оцінки просторових відносин протяжних об'єктів.

Безліч раціональних чисел позначається і може з певною часткою строгості бути записано у вигляді: . Потрібно розуміти, що однакові дроби, такі як, наприклад, і , входять у це безліч як один дріб. Таким чином, можна більш формально говорити про безліч раціональних чисел, як про безліч нескоротних дробів із цілим чисельником та натуральним знаменником: . Тут - найбільший спільний дільник чисел mі n. Його рівність одиниці гарантує взаємну простоту чисельника і знаменника, що, своєю чергою, гарантує нескоротність дробу .

Безліч раціональних чисел є природним узагальненням безлічі цілих чисел. Легко бачити, що якщо у раціонального числа знаменник n= 1 , то a = mє цілим числом. У цьому виникають деякі оманливі припущення. По-перше, здається, що раціональних чисел більше ніж цілих, насправді тих і інших лічильне число. По-друге, виникає припущення, що такими числами можна виміряти абсолютно точно будь-яку відстань у просторі. Насправді, для цього використовуються дійсні числа, раціональних чисел для цього недостатньо.

Термінологія

Формальне визначення

Формально раціональні числа визначаються як безліч класів еквівалентності пар щодо еквівалентності, якщо. При цьому операції складання та множення визначаються таким чином:

Пов'язані визначення

Правильноюназивається дріб, у якого модуль чисельника менший від модуля знаменника. Дроб, що не є правильним, називається неправильною.

Наприклад, дроби , і - правильні дроби, тоді як , і - неправильні дроби. Будь-яке ціле число можна у вигляді неправильного звичайного дробу зі знаменником 1.

Дроб, записаний у вигляді цілого числа та правильного дробу, називається змішаним дробомі розуміється як сума цього числа та дробу.

Наприклад, . У суворій математичній літературі такий запис воліють не використовувати через схожість позначення змішаного дробуз позначенням добутку цілого числа на дріб.

Коментар

Термін дробове число(Дроб)іноді використовується як синонім до терміну раціональне числоа іноді синонім будь-якого нецілого числа. У разі, дробові і раціональні числа є різними речами, оскільки тоді нецілі раціональні числа - лише окремий випадокдробових.

Властивості

Основні властивості

Раціональні числа задовольняють шістнадцяти основним властивостям, які можуть бути отримані з властивостей цілих чисел.

Додаткові властивості

Решта всіх властивостей, властивих раціональним числам, не виділяють в основні, тому що вони, взагалі кажучи, вже не спираються безпосередньо на властивості цілих чисел, а можуть бути доведені виходячи з наведених основних властивостей або безпосередньо за визначенням деякого математичного об'єкта. Таких додаткових властивостей дуже багато. Тут має сенс навести лише деякі з них.

Src="/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png" border="0">

Рахунковість множини

Нумерація раціональних чисел

Щоб оцінити кількість раціональних чисел, потрібно знайти потужність їхньої множини. Легко довести, що безліч раціональних чисел є . Для цього достатньо навести алгоритм, який нумерує раціональні числа, тобто встановлює бієкцію між множинами раціональних і натуральних чисел.

Найпростіший з таких алгоритмів виглядає так. Складається нескінченна таблиця звичайних дробів, на кожному i-ому рядку в кожному j-ом стовпці якої розташовується дріб. Для певності вважається, що рядки та стовпці цієї таблиці нумеруються з одиниці. Осередки таблиці позначаються , де i- номер рядка таблиці, в якій розташовується осередок, а j- Номер стовпця.

Отримана таблиця обходиться «змійкою» за формальним алгоритмом.

Ці правила проглядаються зверху вниз і наступне положення вибирається за першим збігом.

У процесі такого обходу кожному новому раціональному числу ставиться у відповідність чергове натуральне число. Т. е. дробу 1/1 ставиться у відповідність число 1, дробу 2/1 - число 2, і т. д. Потрібно відзначити, що нумеруються тільки нескоротні дроби. Формальною ознакою нескоротності є рівність одиниці найбільшого загального дільника чисельника та знаменника дробу.

Наслідуючи цей алгоритм, можна занумерувати всі позитивні раціональні числа. Це означає, що багато позитивних раціональних чисел лічимо. Легко встановити бієкцію між множинами позитивних і негативних раціональних чисел, просто поставивши у відповідність кожному раціональному числу протилежне йому. Т. о. безліч негативних раціональних чисел теж лічить. Їх об'єднання також лічимо за якістю лічильних множин. Багато ж раціональних чисел теж лічимо як об'єднання лічильної множини з кінцевим.

Твердження про рахунковості безлічі раціональних чисел може викликати деяке здивування, тому що на перший погляд складається враження, що воно набагато ширше за безліч натуральних чисел. Насправді, це не так і натуральних чисел вистачає, щоб занумерувати всі раціональні.

Недостатність раціональних чисел

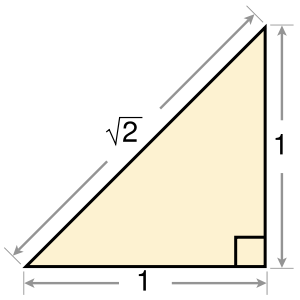
Гіпотенуза такого трикутника не виражається жодним раціональним числом

Раціональними числами виду 1/ nпри великих nможна вимірювати як завгодно малі величини. Цей факт створює оманливе враження, що раціональними числамиможна виміряти взагалі будь-які геометричні відстані. Легко показати, що це не так.

З теореми Піфагора відомо, що гіпотенуза прямокутного трикутника виражається як квадратний корінь суми квадратів його катетів. Т. о. довжина гіпотенузи рівнобедреного прямокутного трикутника з одиничним катетом дорівнює , тобто числу, квадрат якого дорівнює 2.

Якщо припустити, що число є деяким раціональним числом, то знайдеться таке ціле число mі таке натуральне число n, Що , причому дріб нескоротний, тобто числа mі n- Взаємно прості.

Якщо то , тобто. m 2 = 2n 2 . Отже, число m 2 парно, але добуток двох непарних чисел непарно, що означає, що саме число mтакож парно. А значить знайдеться натуральне число k, таке що число mможна уявити у вигляді m = 2k. Квадрат числа mу цьому сенсі m 2 = 4k 2 , але з іншого боку m 2 = 2n 2 , значить 4 k 2 = 2n 2 , або n 2 = 2k 2 . Як показано раніше для числа m, це означає, що число n- парно, як і m. Але тоді вони є взаємно простими, оскільки обоє діляться навпіл. Отримане протиріччя доводить, що немає раціональне число.

Зі сказаного вище, що є відрізки на площині, отже, і числової прямої, які можуть бути виміряні раціональними числами. Це призводить до необхідності розширення поняття раціональних чисел до

Що таке дріб у математиці?

Дроби- Число, складене з однієї або декількох рівних часток одиниці.

Це саме визначення дробу. А більш докладно відповідь на запитання «що таке дріб» (а також що таке «одиниця» у визначенні дробу) представлена нижче на конкретних прикладах, а також у навчальному відео.

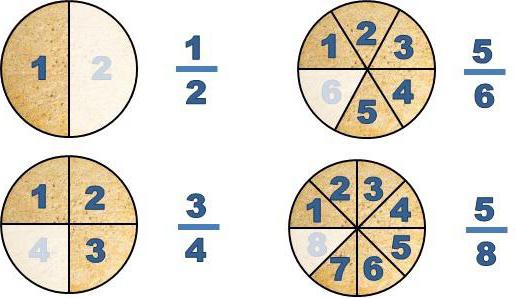
Коло розділили на дві рівні частини, і одну взяли. Маємо дріб ½. Чисельник дробу (1) показує, скільки рівних частин кола взяли (взяли одну частину). Знаменник дробу показує, на скільки рівних частин розділили коло (ділили його на дві рівні частини).

Коло розділили на три рівні частини. Взяли одну частину (тобто 1/3). Взяли дві частини (тобто 2/3).

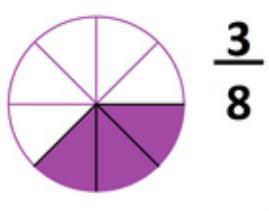
Торт розрізали на 8 рівних шматків. Кожен шматок – це 1/8 торта. Батьку в тарілку поклали два шматки (тобто 2/8 торта), а бабусі - три шматки (тобто 3/8 торта).

Зовсім не обов'язково «одиниця» у визначенні дробу на практиці має бути представлена кругом або тортом (як зазвичай її представляють у прикладах із підручників) або чимось монолітним фізично.

Бабуся купила 18 мотків пряжі. Собі вона залишила 13 мотків (тобто 13/18 покупки), а 5 мотків (тобто 5/18 покупки) віддала внучці. В результаті у онуки виявилося 5/13 того, що залишила собі бабуся. У цьому прикладі спочатку за одиницю було прийнято всю покупку (18/18 = 1), та був - те, що залишила собі бабуся (13/13 = 1).

Що таке змішане число?

Змішане число- Число, до складу якого входить ціле число і дріб. Наприклад, 3½, 97/8. Читається це так: «три цілих, одна друга», «дев'ять цілих, сім восьмих» або «три цілих і одна друга», «дев'ять цілих та сім восьмих». Іноді слово «цілих» пропускають і кажуть так: «три та одна друга», «дев'ять і сім восьмих». Число 3½ можна уявити, наприклад, як три цілих торта (обов'язково однакових) і половину від четвертого такого ж торта. Наочно відповідь на запитання «що таке змішане число» представлено в навчальному відео.

Правильні та неправильні дроби

Чисельник може бути меншим за знаменник, більшим за знаменник або дорівнює йому. Залежно від цього розрізняють дроби «правильні» та «неправильні».

Правильний дріб- дріб, у якого чисельник менший за знаменник. Наприклад, ½, 5/6, 9/10, 11/125, 144/145.

Неправильний дріб- дріб, у якого чисельник більший за знаменник або дорівнює йому. Наприклад, 3/2, 6/5, 10/9, 125/125, 145/144.

Як уявити у своїй уяві правильний дріб - описано в прикладах вище. А неправильний дріб можна так (див. приклади нижче).

На святкування дня народження купили два однакові торти. Їх обидва порізали на однакове числошматків (на 8 шматків порізали перший торт і стільки ж шматків порізали другий торт, всього вийшло 8 + 8 = 16 однакових шматків). Але гарячі страви виявилися настільки калорійними, що перший торт був з'їдений не весь (5 шматків було з'їдено, а 3 шматки залишилися на блюді), а другий торт (8 шматків) взагалі залишився недоторканим. Всього було з'їдено 5/8 одного торта, або 5/16 всього десерту. (5/8 та 5/16 - правильні дроби). А що лишилося? Залишився один цілий торт (нарізаний на 8 шматків, тобто 1 = 8/8) та ще 3/8 такого ж торта. Тобто. залишилося 11/8 торта (одинадцять восьмих, це неправильний дріб, т.к. чисельник більший за знаменник).

Звернення неправильного дробу в змішане число

Щоб звернути неправильний дріб у змішане число, потрібно чисельник дробу поділити на знаменник та знайти залишок; приватне покаже число цілих одиниць, а залишок - число часток одиниці.

Потрібно звернути неправильний дріб 25/4 у змішане число.

1) Ділити 25 на 4. Цілих виходить 6.

2) Помножити 6 (цілих) на 4 (знаменник), результат дорівнює 24.

3) Відняти 24 з 25 - і виходить залишок 1.

В результаті отримано змішане число 61/4 (шість цілих та одна четверта).

Потрібно звернути неправильний дріб 106/14 у змішане число.

Послідовність дій така.

1) Ділити 106 на 14. Цілих виходить 7.

2) Помножити 7 (цілих) на 14 (знаменник), результат дорівнює 98.

3) 106 - 98 = 8.

В результаті отримано змішане число 78/14 (сім цілих та вісім чотирнадцятих).

Відповідь на запитання " З якого дробу можна виділити цілу частину?» наступний. У правильному дробі чисельник менший за знаменник, отже, результат розподілу чисельника на знаменник менший за одиницю. Тому із правильного дробу виділити цілу частину не можна. Цілу частину можна виділити з неправильного дробу, у процесі її звернення до змішаного числа. Ця процедура розглянута в прикладах вище, а також наочно показана в навчальному відео.

Перетворення змішаного числа в неправильний дріб

Щоб звернути змішане число в неправильний дріб, потрібно:

Знаменник помножити на цілу частину;

До отриманого твору додати чисельник, зробити цю суму чисельником шуканого дробу, а знаменник залишити колишній.

Нижче змішані числа з попередніх прикладів (61/4 та 78/14) знову перетворені на неправильні дроби:

Потрібне змішане число 61/4 звернути до неправильного дробу.

6 (цілих) * 4 (знаменник) = 24,

24 + 1 (числитель) = 25 (буде чисельником неправильного дробу),

Неправильний дріб: 25/4.

Потрібно змішати число 78/14 звернути в неправильний дріб.

7 (цілих) * 14 (знаменник) = 98,

98 + 8 (числитель) = 106 (буде чисельником неправильного дробу),

Неправильний дріб: 106/14.

Інші приклади.

63/4 = (6*4 + 3)/4 = (24+3)/4 = 27/4

53/8 = (5*8 + 3)/8 = (40+3) / 8 = 43/8

2514/88 = (25*88 + 14)/88 = (2200 + 14) / 88 = 2214/88

Основна властивість дробу

При одночасному збільшенні чи зменшенні чисельника та знаменника в однакове число разів дріб не зміниться.

Уявити це можна так. Розрізали торт на чотири рівні частини і одну взяли собі. Тобто. взяли ¼ торта. Але кожен шматок можна розрізати, наприклад, навпіл (а весь торт при цьому був би розрізаний не на 4, а на 8 рівних частин). Наша частка залишилася б колишньою (1/4), але складалася б вона з двох шматків меншою вдвічі величини (тобто 2/8). Або торт можна було б розрізати не так на 4 і не на 8, а на 12 рівних частин. Взяли б ми тоді собі 3 шматки (тобто 3/12). Але і 2/8, і 3/12 складає ту ж частину ¼ торта. Не більше, не менше.

Як і навіщо скорочувати дроби

Скороченням дробу називається заміна його інший, що дорівнює їй дробом з меншими членами, шляхом розподілу чисельника і знаменника на одне й те саме число.

Таким чином, скорочення дробу засноване на основному її властивості.

Навіщо скорочувати дроби? Взяту частину торта з попереднього прикладу (3/12 або 2/8) легше уявити у своїй уяві, якщо ці дроби скоротити. У дробі 3/12 і чисельник і знаменник діляться без залишку на 3, результат - ¼. У дробі 2/8 і чисельник і знаменник діляться без залишку на 2, результат - ¼. Уявити ¼ торта набагато легше, ніж уявити 2/8, 3/12 або 6/24 торта.

Інші приклади скорочення дробів:

18/56 = (2*9) / (2*28) = 9/28

27/33 = (3*9) / (3*11) = 9/11

30/250 = (3*10) / (25*10) = 3/25

Іноді ставлять питання « Чи можна скорочувати дроби при їх складанні та відніманні?». Можна і треба скорочувати ці дроби, тільки в жодному разі не «друга з одним», тобто. не чисельник одного дробу зі знаменником іншого. Скорочувати потрібно кожен дріб окремо, але потрібно при цьому пам'ятати і про те, що дроби для їхнього складання або віднімання повинні бути приведені до одного спільного знаменника (і бажано саме до найменшого спільного знаменника). А ось при множенні дробів скорочувати можна чисельник дробу зі знаменником як цього дробу, так і зі знаменником іншого дробу. Оскільки розподіл дробів замінюється операцією множення, то вище можна поширити і операцію розподілу дробів. Рекомендується завантажитинаведені приклади з дробами, де були виконані такі перетворення.

Додавання та віднімання дробів з однаковими знаменниками

Щоб скласти дроби з однаковими знаменниками, треба скласти їх числа, а знаменник залишити колишній.

Наприклад,

3/5 + 1/5 = 4/5 (склали чисельники 3 + 1 = 4, а знаменник (5) залишили колишній).

Щоб виконати віднімання дробів з однаковими знаменниками, потрібно відняти чисельник віднімається з чисельника зменшуваного, а знаменник дробу залишити колишній.

Наприклад,

6/15 – 4/15 = 2/15 (числитель 6 – 4 = 2, знаменник (15) колишній).

Приведення дробів до найменшого спільного знаменника

Щоб виконати додавання або віднімання дробів, що мають різні знаменники, потрібно попередньо привести їх до спільного знаменника. Цим знаменником має стати спільне кратне знаменників даних дробів.

Наприклад, дроби 2/5 і 3/15 можна було б призвести до спільного знаменника 15, 30, 45, 75, 150 або ще більшого, але обсяг обчислювальної роботи буде набагато меншим, якщо приводити дроби саме до найменшого загального знаменника (у даному випадку - 15).

Щоб привести дроби до найменшого спільного знаменника, потрібно:

Знайти найменше загальне кратне всіх знаменників;

Для кожного знаменника визначити додатковий множник (розділивши новий знаменник на колишній);

Чисельник та знаменник кожного дробу помножити на відповідний додатковий множник його знаменника.

Дроби 2/5 і 3/15 .

Знаменник другого дробу: 15 = 3 * 5

Найменше загальне кратне знаменників: 3 * 5 = 15 (новий знаменник дробів)

Додатковий множник для знаменника першого дробу: 15/5 = 3

Додатковий множник для знаменника другого дробу: 15/15 = 1

Новий чисельник першого дробу: 3*2 = 6

Новий чисельник другого дробу: 3 (у цьому випадку перший дріб наводиться до знаменника другого дробу).

Отже, відповідь: 6/15 та 3/15.

Дроби 2/5 і 4/7 .

Знаменник першого дробу: 5 = 1 * 5

Знаменник другого дробу: 7 = 1 * 7

Найменше загальне кратне знаменників: 5 * 7 = 35 (новий знаменник дробів)

Додатковий множник для знаменника першого дробу: 35/5 = 7

Додатковий множник для знаменника другого дробу: 35/7 = 5

Новий чисельник першого дробу: 7*2 = 14

Новий чисельник другого дробу: 5 * 4 = 20.

Отже, відповідь: 14/35 та 20/35.

Дроби 2/15 і 7/12 .

Знаменник першого дробу: 15 = 3 * 5

Знаменник другого дробу: 12 = 3 * 4

Найменше загальне кратне знаменників: 3*4*5 = 60 (новий знаменник дробів)

Додатковий множник для знаменника першого дробу: 60/15 = 4

Додатковий множник для знаменника другого дробу: 60/12 = 5

Новий чисельник першого дробу: 4*2 = 8

Новий чисельник другого дробу: 5 * 7 = 35.

Отже, відповідь: 8/60 та 35/60.

Дроби 2/21, 5/24 і 3/16 .

Знаменник першого дробу: 21 = 3 * 7

Знаменник другого дробу: 24 = 2 * 12 = 2 * 2 * 6 = 2 * 2 * 2 * 3

Знаменник третього дробу: 16 = 2 * 8 = 2 * 2 * 4 = 2 * 2 * 2 * 2

Найменше загальне кратне знаменників: 2*2*2*2*3*7= 336 (новий знаменник дробів)

Додатковий множник для знаменника першого дробу: 336/21 = 16

Додатковий множник для знаменника другого дробу: 336/24 = 14

Додатковий множник для знаменника третього дробу: 336/16 = 21

Новий чисельник першого дробу: 2*16 = 32

Новий чисельник другого дробу: 5*14 = 70

Новий чисельник третього дробу: 3*21 = 63

Отже, відповідь: 32/336, 70/336 та 63/336.

Додавання та віднімання дробів з різними знаменниками (тобто складання та віднімання дробів, що мають різні знаменники)

Таким чином,

2/21 + 5/24 + 3/16 = 32/336 + 70/336 + 63/336 = (32 + 70 + 63)/336 = 165/336

Додавання дробів з різними знаменниками(тобто складання дробів, що мають різні знаменники)

Щоб скласти дроби з різними знаменниками, потрібно заздалегідь привести їх до найменшого спільного знаменника, скласти їх чисельники та підписати спільний знаменник.

Наприклад, потрібно скласти дроби 2/21, 5/24 та 3/16.

Приведення їх до найменшого загального знаменника докладно описано у прикладі №4.

Таким чином,

2/21 + 5/24 + 3/16 = 32/336 + 70/336 + 63/336 = (32 + 70 + 63)/336 = 165/336.

Віднімання дробів із різними знаменниками(тобто віднімання дробів, що мають різні знаменники)

Щоб відняти дроби з різними знаменниками, потрібно попередньо привести їх до найменшого загального знаменника, відняти чисельник віднімається з чисельника зменшуваного і підписати загальний знаменник.

5/24 - 2/21 = 70/336 - 32/336 = 38/336.

Залишати відповідь у такому вигляді математично «некультурно». Дроби потрібно скоротити: 38/336 = (2 * 19) / (2 * 168) = 19 / 168. Однак, скорочувати дріб довелося через те, що знаменник 336 був найменшим загальним знаменником трьох дробів 2/21 + 5/24 + 3/16, розглянутих у попередньому прикладі, але не є найменшим загальним знаменником дробів двох дробів 5/24 та 2 /21 (а є загальним знаменником).

А вчинити спочатку слід було так:

24 = 2*12 = 2*2*6 = 2*2*2*3

НОК(24,21) = 2*2*2*3*7 = 168 (найменший загальний знаменник дробів 5/24 та 2/21)

168/24*5 = 7*5 = 35 (числитель першого дробу)

168/21*2 = 8*2 = 16 (числитель другого дробу)

5/24 - 2/21 = 35/168 - 16/168 = 19/168.

Отримано ту саму відповідь, але швидше і оперуючи меншими числами.

Отже, відповідь: 5/24 – 2/21 = 19/168.

Порівняння дробів

Щоб порівняти дроби, що мають однакові знаменники, потрібно порівняти чисельники цих дробів.

Наприклад,

Щоб порівняти дроби, що мають різні знаменники, потрібно привести їх до спільного знаменника, а потім порівняти нові чисельники дробів. Краще приводити дроби до найменшого спільного знаменника, тому набагато скорочується обсяг обчислювальної роботи.

Потрібно порівняти дроби 2/21 та 3/16.

НОК(21, 16) = 2 * 2 * 2 * 2 * 3 * 7 = 336

63>32, отже дріб 63/336 більший за дроби 32/336, і 3/16> 2/21, а 2/21< 3/16.

Додавання та віднімання змішаних чисел

Іноді питання ставлять так: «Як складати змішані дроби?», «Як віднімати змішані дроби?». Це не коректно. Є дробові числа, які і називають просто «дрібницями» (наприклад, 5/7 або 8/49), а є змішані числа, що складаються з цілої та дробової частини (наприклад, 18/9, 12513/14). Немає такого поняття «змішаний дріб». Питання має звучати так: « Як складати змішані числа?» або « Як віднімати змішані числа?».

Послідовно потрібно скласти (відняти) цілі та дробові частини. При необхідності дробові частини потрібно привести до спільного знаменника.

Бувають випадки, коли дробова частина віднімається більше дробової частини зменшуваного. У разі потрібно взяти одну одиницю з цілої частини зменшуваного, роздробити їх у ті частки, у яких виражена дробова частина, і додати до дробової частини зменшуваного.

51/8 + 3/8 = 54/8 = 51/2

102/21 + 5/24 + 63/16 = 1032/336 + 70/336 +663/336 = 10 + 6 + (32 + 70 + 63)/336 = 16 + 165/336 = 16165/336.

53/16 - 12/21 = 5 - 1 + 3/16 - 2/21 = 4 + 63/336 — 32/336 = 4 + (63 — 32)/336 = 4 + 31/336 = 431/336

72/21 - 33/16 = 7 - 3 + 2/21 - 3/16 = 4 + 32/336 — 63/336 = 3 + 1 + 32/336 - 63/336 = 3 + 336/336 + 32/336 - 63/336 = 3 + (336 + 32 — 63)/336 = 3 + 305/336 = 3305/336

Оскільки питання « Як складати дроби з цілим числомХтось може трактувати помилково, відповідь на це питання тут розглядається докладно. Якщо мається на увазі додавання дробу до цілого числа (наприклад, до двох потрібно додати дві третини, тобто 2 + 2/3), то відповідь буде змішаним числом, ціла частина якого дорівнює цілому числу - доданку (в цьому прикладі це число «2»), а дробова частина дорівнює дробу (у цьому прикладі це 2/3). Тобто. 2+2/3 = 22/3. Інший приклад: 15+7/24 = 157/24. Якщо ж у цьому питанні хтось під фразою «дроб з цілим числом» розуміє змішане число – це некоректно. Тоді питання слід ставити як «складання змішаних чисел», «як складати змішані числа».

Розмноження цілого числа на дріб

Щоб помножити ціле число на дріб, Треба помножити ціле число на чисельник цього дробу і цей твір зробити чисельником, а знаменником підписати знаменник даного дробу.

Аналогічно, щоб помножити дріб на ціле число, Треба помножити чисельник дробу на ціле число і цей твір зробити чисельником, а знаменником підписати знаменник даного дробу.

3* 5/8 = (3*5) / 8 = 15/8 = 17/8

Розмноження дробів

При множенні дробів немає жодної різниці в тому, чи однакові їх знаменники або вони різні. Тому питання « як множити дроби з однаковими знаменниками», « як множити дроби з різними знаменниками» та « як множити дроби з різними знаменниками та чисельниками» Особливого сенсу немає. Відповіді на них ті ж, що й на відомі, найпоширеніші питання. як множити дроби», « як помножити дріб на дріб».

Правило множення дробівнаступне.

Щоб помножити дріб на дріб, Потрібно помножити чисельник на чисельник (це буде чисельник твору), а знаменник - на знаменник (це буде знаменник твору).

2/3 * 5/6 = (2*5) / (3*6) = 10/18

Дроби 10/18 потрібно ще скоротити: 10/18 = (2 * 5) / (2 * 9) = 5 / 9.

Але можна було вчинити інакше (що краще):

2/3 * 5/6 = (2*5) / (3*6) = (2*5) / (3*2*3) = 5 / (3*3) = 5/9

Якщо один або кілька співмножників мають знак мінус - знак твору визначають так само, як і при множенні цілих чисел з різними знаками.

Розмноження змішаного числа на ціле число

Щоб помножити змішане число на ціле, потрібно заздалегідь звернути змішане число в неправильний дріб і потім перемножити за правилом множення дробу на ціле число.

21/3 * 4 = 7/3 * 4 = (7*4) / 3 = 28/3 = 91/3

6 * 58/9 = 6 * (5*9 + 8)/9 = 6* (45+8)/9 = 6* 53/9 = 2*3*53/(3*3) = 2*53/3 = 106/3 = 351/3

Як відомо, до багатьох цілих чисел відносяться натуральні числа, їм протилежні (тобто зі знаком «мінус») та нуль. Тому множення змішаного числа на натуральне число- це окремий випадок, на який так само поширюється правило множення змішаного числа на ціле число. Іноді це питання формулюють некоректно: як множити змішані дроби на натуральне число. Немає поняття "змішані дроби", є змішані числа.

Розмноження змішаних чисел

Іноді питання ставлять так: «Як множити змішані дроби?». Це некоректно, як вже було сказано вище, коли розбиралися подібні некоректні питання про складання та множення змішаних дробів. Питання має звучати так: «Як множити змішані числа?».

Щоб перемножити змішані числа, потрібно попередньо звернути їх у неправильні дроби і потім перемножити за правилом множення дробу на дріб.

27/8 * 35/11 = [(2*8 + 7)/8] * [(3*11 + 5)/11] = [(16+7)/8] * [(33+5)/11] = 23/8 * 38/11 = * [(2*19)/11] = 23/4 * 19/11 = (23*19) / (4*11) = 437 / 44 = 941/44

Тут у процесі рішення було виконано скорочення дробів (зменшення чисельника та знаменника в однакове число разів, у даному випадку – у два рази). Якби цього не було зроблено в процесі рішення, а були б просто перемножені чисельники та знаменники, результат був би наступним:

27/8 * 35/11 = 23/8 * 38/11 = (23*38) / (8*11) = 874/88

Як видно, такий дріб треба скорочувати:

27/8 * 35/11 = 23/8 * 38/11 = 874/88 = (437*2)/(44*2) = 437/44

Цим прикладом проілюстровано, що, не виробляючи скорочення дробів у процесі рішення, доводиться оперувати великими числами, а дріб, отриманий в результаті, так само доводиться скорочувати. Краще проводити скорочення у процесі рішення.

Питання "Як множити дроби з цілим числом" некоректний. Якщо під "дрібницями з цілим числом" мається на увазі змішане число - читайте про множення змішаних чисел. Якщо ж мається на увазі збільшення дробу на ціле число - читайте про те, як помножити ціле число на дріб.

Зворотні дроби

Розуміння того, що таке зворотний дріб, дуже важливо задля освоєння процедури розподілу дробів. Взаємно зворотні дробиназиваються два дроби, які мають тим властивістю, що чисельник першої є знаменником другої, а знаменник першої є чисельником другої.

Наприклад, взаємно зворотнимиє дроби 4/5 та 5/4, 11/148 та 148/11.

Для всіх чисел із чисельником «1» оберненими будуть цілі числа. Щоб написати число, зворотне цілому, треба поставити це число знаменником, а чисельником дорівнюватиме 1.

Наприклад, взаємно зворотними будуть числа 7 та 1/7, 25 та 1/25, 1/48 та 48, 1/3 та 3.

Взаємно зворотні числа мають наступний властивістю: твір взаємно зворотних чиселодно одиниці.

Розподіл цілого числа на дріб

Щоб розділити число на дріб, треба це ціле число помножити на знаменник даного дробу і, зробивши цей твір чисельником, розділити його на чисельник даного дробу.

Це правило можна записати так:

a: (b/c) = (ac)/b

5/ (2/3) = (5*3)/2 = 15/2 = 71/2

8/ (6/21) = (8*21) / 6 = (2*4*21) / (2*3) = (4*21) / 3 = (4*3*7) / 3 = 4*7 = 28

Розподіл дробів

При розподілі дробів немає значення, однакові чи різні їх знаменники. Тому питання « Як ділити дроби з різними знаменниками та чисельниками», « Як ділити дроби з різними знаменниками», « Як ділити дроби з однаковими знаменниками» Особливого сенсу немає. Відповіді на них ті ж, що і на питання про те, як ділити дроби.

Щоб розділити дріб на дріб, потрібно чисельник першого дробу помножити на знаменник другого (це буде чисельник нового дробу), а знаменник першого дробу помножити на чисельник другого (це знаменник нового дробу).

Можна сказати інакше:

Щоб розділити дріб на дріб, потрібно перший дріб (ділене) помножити на дріб, зворотний другий (дільнику) (тобто перший дріб потрібно помножити на «перевернутий» другий дріб).

(4/5):(3/11) = (4/5)*(11/3) = (4*11)/(5*3) = 44/15 = 214/15

(6/7):(2/9) = (4/5)*(11/3) = (4*11)/(5*3) = 44/15 = 214/15

Про те, як працювати з буквено-числовими виразами (ділити їх, віднімати, множити, складати), йдеться у шкільному курсі алгебри. Це питання не торкається цієї статті, присвяченої звичайним і десятковим дробам. Однак, дається застереження: іноді школярі помилково «ділять» sin(x) на cos(x), скорочують однакові літери «s» та однакові літери «х» у чисельнику та знаменнику та отримують «результат» in/co. Це абсолютно неписьменно, т.к. sin(x) і cos(x) - тригонометричні функції, а не добуток змінних "s", "i", "n", "x" і "c", "o", "s", "x".

Якщо ділене або дільники мають знак «мінус» — приватний знак визначають так само, як і при розподілі цілих чисел з різними знаками.

Розподіл змішаних чисел

Іноді питання ставлять так: «Як ділити змішані дроби?». Вище вже було сказано про те, що поняття «змішаний дріб» немає. Питання має звучати так: «Як ділити змішані числа?».

Щоб розділити одне змішане число на інше, потрібно заздалегідь звернути їх у неправильні дроби і потім розділити за правилом поділу дробу на дріб.

27/8: 35/11 = [(2*8 + 7)/8] : [(3*11 + 5)/11] = [(16+7)/8] : [(33+5)/11] = 23/8: 38/11 =

=(23/8) * (11/38) = (23*11) / (8*38) = 253 / 304.

Десяткові дроби

Розрізняють дроби звичайні та дроби десяткові. Звичайні дробипредставлені у вигляді чисельника та знаменника, розділених горизонтальною межею. Коли немає можливості поставити горизонтальну межу, користуються косою межею (наприклад, 7/11, 6/125, 39/1572). Знаменниками ж д есятинних дробівє лише числа, зображувані одиницею з наступними нулями (одним чи кількома), наприклад 7/10, 6/100, 39/1000. Ті ж 7/10, 6/100 та 39/1000 можна подати у вигляді десяткового дробу без знаменника: 0,7; 0,06; 0,039 (читається: сім десятих, шість сотих, тридцять дев'ять тисячних).

Порівняння десяткових дробів

З двох десяткових дробів той більший, у якого число цілих більше; при рівності цілих той дріб більший, у якого число десятих більше; при рівності цілих і десятих той дріб більший, у якого число сотих більше, і т.д.

Наприклад,

3,125 < 5,016

0,078 > 0,069

0,412 > 0,300257

0,7825 < 0,784

Дії над десятковими дробами

Щоб збільшитидесятковий дріб у 10 разівпотрібно перенести кому в ній на один знак вправо; щоб збільшити її в 100 разів, потрібно перенести кому на два знаки праворуч; щоб збільшити її в 1000 разів – на три знаки вправо, і т.д. Якщо при цьому не вистачає знаків у числа, то приписують до нього праворуч.

Щоб зменшитидесятковий дріб у 10 разівпотрібно перенести кому в ній на один знак вліво; щоб зменшити її в 100 разів, потрібно перенести кому на два знаки вліво; щоб зменшити її у 1000 разів – на три знаки вліво, і т.д. Якщо при цьому не вистачає знаків у числа, то приписують до нього зліва нулі.

Наприклад,

2,05*1000 = 2050

2,05/100 = 0,0205

При складання десяткових дробівтреба дотримуватися наступного порядку: дроби підписувати одна під одною так, щоб у всіх доданків однакові розряди знаходилися один під одним і всі коми стояли в тому самому вертикальному стовпці; праворуч від десяткових знаків деяких доданків приписують, хоча б подумки, таку кількість нулів, щоб усі доданки після коми мали однакове число цифр. Потім виконують додавання по розрядах, починаючи з правої сторони, і в отриманій сумі ставлять кому в тому самому вертикальному стовпці, в якому вона знаходиться в даних доданків.

Наприклад, потрібно скласти 1,905+0,3+7,8814

При віднімання десяткових дробівтреба дотримуватися наступного порядку: підписують віднімається під зменшуваним так, щоб однакові розряди знаходилися один під одним і всі коми стояли в тому самому вертикальному стовпці; праворуч приписують, хоча б подумки, в зменшуваному або віднімається стільки нулів, щоб вони мали однакову кількість десяткових знаків, потім виконують віднімання по розрядах, починаючи з правого боку, і в отриманій різниці ставлять кому в тому самому вертикальному стовпці, в якому вона знаходиться в зменшуваному і віднімається.

Наприклад, потрібно виконати віднімання 145,501 - 3,040652 - 17,89

Щоб перемножитидва десяткові дроби, достатньо, не звертаючи уваги на коми, перемножити їх як цілі числа та у творі відокремити коми з правого боку стільки десяткових знаків, скільки їх було у множині та множнику разом.

Наприклад,

127,0206*4,03 = 511,893018

7,31*2,4 = 17,544

Розподіл десяткового дробу на ціле числовиконується так само, як і розподіл цілих чисел, причому залишки, що виходять, звертають в десяткові частки, все більше і дрібніші; розподіл продовжують до того часу, поки залишку не вийде нуль чи залишок стане зневажливо малим (з його розряду).

Щоб розділити число на десятковий дріб, потрібно відкинути в дільнику кому, а потім збільшити ділене у стільки разів, у скільки збільшився дільник при відкиданні в ньому комою, після чого виконати поділ за правилом поділу на ціле число.

Наприклад, 5/3,05 = 500/305 ≈ 1,639344

Навіщо в школі вивчають дроби

Тема «дробі» досить важко дається майже всім школярам, виняток становлять лише 3 - 5 чоловік із класу, найбільш кмітливі та найбільш підготовлені до навчання у школі. Але й інші можуть (і повинні) її освоїти шляхом систематичних занять, вирішення достатньої кількості прикладів, сприяють виробленню техніки обчислень, і завдань, сприяють глибшому розумінню цієї теми. Адже дроби оточують нас у житті всюди: хіба є людина, яка не знає про існування півлітрової (0,5 л або ½ л) банки або про те, що нормальна температура її тіла має становити 36,6 градусів? І, насправді, кожен знає, що вміст двох півлітрових банок можна злити в одну літрову, а вміст двох 1,5 л пляшок - у трилітровий сулій, просто в цей момент ніхто не замислюється про те, що він зараз складає дроби. . А хіба хтось не вміє порівнювати десяткові дроби? Чи є хтось, який не знає, що температура тіла 36,9 - вище, ніж 36,6? Але це лише найпростіші приклади з повсякденного життя будь-якої людини. Людям технічних і природничо-наукових спеціальностей доводиться у своїй професійній діяльності вирішувати складніші завдання, пов'язані з дробовими числами. Розуміння теми «дроби» стане в нагоді і за подальшому вивченні математики у середній школі, тобто. алгебри та геометрії.

Приклади розв'язання задач на дії з дробами

Першого дня шибки склали 35 вікон, що становить 1/8 всіх вікон збудованого будинку. Скільки всього вікон у будинку?

За умови завдання сказано, що засклені 35 вікон становлять 1/8 всіх вікон збудованого будинку. Отже, лише вікон у 8 разів більше, тобто.

35 * 8 = 280 вікон.

Магазин за місяць продав 2730 кг цукру, що становить 3/7 всього запасу цукру, що був у магазині. Яким був первинний запас цукру в магазині?

Весь наявний запас - це 7/7.

1/7 запасу складає 2730/3 = 910 кг.

Весь наявний запас становив 910 * 7 = 6370 кг.

При цьому число mназивається чисельником, а число n - знаменникомдроби. Такий дріб слід інтуїтивно розуміти, як результат поділу mна nнавіть якщо націло розділити не вдається. У реальному житті можна використовувати раціональні числа для рахунку частин деяких цілих, але поділених об'єктів, наприклад, тортівабо інших продуктів, що розрізаються на кілька частин перед вживанням, або для грубої оцінки просторових відносин протяжних об'єктів.

Безліч раціональних чисел позначається і може з певною часткою строгості бути записано у вигляді: . Потрібно розуміти, що однакові дроби, такі як, наприклад, і , входять до цього безліч як один дріб. Таким чином, можна більш формально говорити про безліч раціональних чисел, як про безліч нескоротних дробів із цілим чисельником та натуральним знаменником: . Тут - найбільший спільний дільникчисел mі n. Його рівність одиниці гарантує взаємну простотучисельника та знаменника, що, у свою чергу, гарантує нескоротність дробу .

Безліч раціональних чисел є природним узагальненням безлічі цілих чисел. Легко бачити, що якщо у раціонального числа знаменник n= 1 , то a = mє цілим числом. У цьому виникають деякі оманливі припущення. По-перше, здається, що раціональних чисел більше ніж цілих, насправді тих і інших. лічильне число. По-друге, виникає припущення, що такими числами можна виміряти абсолютно точно будь-яку відстань у просторі. Насправді для цього використовуються дійсні числа, раціональних чисел для цього недостатньо.

Термінологія

Формальне визначення

Формально раціональні числа визначаються як безліч класів еквівалентності пар за відношенню еквівалентностіякщо . При цьому операції складання та множення визначаються таким чином:

Пов'язані визначення

Наприклад, . У суворій математичній літературі такий запис воліють не використовувати через схожість позначення змішаного дробу з позначенням добутку цілого числа на дріб.

Коментар

Термін дробове число (дроб)іноді використовується як синонім до терміну раціональне числоа іноді синонім будь-якого нецілого числа. У разі, дробові і раціональні числа є різними речами, оскільки тоді нецілі раціональні числа - лише окремий випадок дробових.

Властивості

Основні властивості

Раціональні числа задовольняють шістнадцять основних властивостям, які легко можуть бути отримані з властивостей цілих чисел.

Додаткові властивості

Src="/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png" border="0">

Рахунковість множини

Нумерація раціональних чисел

Щоб оцінити кількість раціональних чисел, потрібно знайти потужністьїх множини. Легко довести, що багато раціональних чисел рахунково. Для цього достатньо навести алгоритм, що нумерує раціональні числа, тобто встановлює бієкціюміж множинами раціональних та натуральних чисел.

Отримана таблиця обходиться «змійкою» за формальним алгоритмом.

Ці правила проглядаються зверху вниз і наступне положення вибирається за першим збігом.

У процесі такого обходу кожному новому раціональному числу ставиться у відповідність чергове натуральне число. Т. е. дробу 1/1 ставиться у відповідність число 1, дробу 2/1 - число 2, і т. д. Потрібно відзначити, що нумеруються тільки нескоротні дроби. Формальною ознакою нескоротності є рівність одиниці найбільшого спільного дільникачисельника та знаменника дробу.

Недостатність раціональних чисел

Гіпотенуза такого трикутника не виражається жодним раціональним числом

Раціональними числами виду 1/ nпри великих nможна вимірювати скільки завгодно малі величини. Цей факт створює оманливе враження, що раціональними числами можна виміряти взагалі будь-які геометричні відстані. Легко показати, що це не так.