Раціональні числа, як позначаються. Раціональні числа

)- це числа з позитивним або негативним знаком (цілі та дробові) і нуль. Точніше поняття раціональних чисел, звучить так:

Раціональне число - Число, яке представляється звичайним дробом m/n, де чисельник m- Цілі числа, а знаменник n- натуральні числа, наприклад 2/3.

Нескінченні неперіодичні дроби НЕ входять до множини раціональних чисел.

a/b, де a∈ Z (aналежить цілим числам), b∈ N (bналежить натуральним числам).

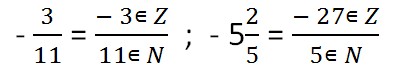
Використання раціональних чисел у реальному житті.

У реальному житті безліч раціональних чисел використовується для рахунку частин деяких цілих поділених об'єктів, наприклад, Торти або інші продукти, що розрізаються на частини перед вживанням, або для грубої оцінки просторових відносин протяжних об'єктів.

Властивості раціональних чисел.

Основні властивості раціональних чисел.

1. Упорядкованість aі bє правило, яке дозволяє однозначно ідентифікувати між ними одно і лише одне з трьох відносин: «<», «>» або «=». Це правило - правило впорядкуванняі формулюють його ось так:

• 2 позитивних числа a=m a /n aі b=m b /n bпов'язані тим самим ставленням, як і 2 цілих числа m a⋅ n bі m b⋅ n a;
• 2 негативних числа aі bпов'язані одним ставленням, що і 2 позитивні числа |b|і |a|;
• коли aпозитивно, а b- негативно, то a>b.

∀ a,b∈ Q (a ∨ a>b∨ a = b)

2. Операція додавання. Для всіх раціональних чисел aі bє правило підсумовування, яке ставить їм у відповідність певне раціональне число c. При цьому саме число c- це сумачисел aі bі її позначають як (a+b) підсумовування.

Правило підсумовуваннявиглядає так:

m a/n a +m b/n b = (m a⋅ n b +m b⋅ n a)/(n a⋅ b).

∀ a,b∈ Q∃ !(a+b)∈ Q

3. Операція множення. Для будь-яких раціональних чисел aі bє правило множення, воно ставить їм у відповідність певне раціональне число c. Число c називають творомчисел aі bі позначають (a⋅b), а процес знаходження цієї кількості називають множення.

Правило множеннявиглядає так: m a n a⋅ m b n b = m a⋅ m b n a⋅ n b.

∀a,b∈Q ∃(a⋅b)∈Q

4. Транзитивність відносин порядку.Для будь-яких трьох раціональних чисел a, bі cякщо aменше bі bменше c, то aменше c, а якщо aодно bі bодно c, то aодно c.

∀ a,b,c∈ Q (a ∧ b ⇒ a ∧ (a = b∧ b = c⇒ a = c)

5. Комутативність складання. Від зміни місць раціональних доданків сума не змінюється.

∀ a,b∈ Q a+b=b+a

6. Асоціативність додавання. Порядок складання 3-х раціональних чисел не впливає результат.

∀ a,b,c∈ Q (a+b)+c=a+(b+c)

7. Наявність нуля. Є раціональне число 0, воно зберігає будь-яке інше раціональне число під час складання.

∃ 0 ∈ Q∀ a∈ Q a+0=a

8. Наявність протилежних чисел. У будь-якого раціонального числа є протилежне раціональне число, за їх складання виходить 0.

∀ a∈ Q∃ (−a)∈ Q a+(−a)=0

9. Комутативність множення. Від зміни місць раціональних множників твір не змінюється.

∀ a,b∈ Q a⋅ b=b⋅ a

10. Асоціативність множення. Порядок перемноження 3-х раціональних чисел немає впливу результат.

∀ a,b,c∈ Q (a⋅ b)⋅ c=a⋅ (b⋅ c)

11. Наявність одиниці. Є раціональне число 1, воно зберігає будь-яке інше раціональне число у процесі множення.

∃ 1 ∈ Q∀ a∈ Q a⋅ 1=a

12. Наявність зворотних чисел . Будь-яке раціональне число, відмінне від нуля, має зворотне раціональне число, помноживши на яке отримаємо 1 .

∀ a∈ Q∃ a−1∈ Q a⋅ a−1=1

13. Дистрибутивність множення щодо додавання. Операція множення пов'язана зі складанням за допомогою розподільчого закону:

∀ a,b,c∈ Q (a+b)⋅ c=a⋅ c+b⋅ c

14. Зв'язок відносин порядку з операцією додавання. До лівої і правої частин раціонального нерівності додають те саме раціональне число.

∀ a,b,c∈ Q a ⇒ a+c

15. Зв'язок відносин порядку з операцією множення. Ліву та праву частини раціональної нерівності можна помножити на однакове невід'ємне раціональне число.

∀ a,b,c∈ Q c>0∧ a ⇒ a⋅ c ⋅ c

16. Аксіома Архімеда. Яким би не було раціональне число a, легко взяти стільки одиниць, що їх сума буде більшою a.

Решта всіх властивостей, властивих раціональним числам, не виділяють в основні, тому що вони, взагалі кажучи, вже не спираються безпосередньо на властивості цілих чисел, а можуть бути доведені виходячи з наведених основних властивостей або безпосередньо за визначенням деякого математичного об'єкта. Таких додаткових властивостей дуже багато. Тут має сенс навести лише деякі з них.

Рахунковість множини

Щоб оцінити кількість раціональних чисел, потрібно знайти потужність їхньої множини. Легко довести, що безліч раціональних чисел є . Для цього достатньо навести алгоритм, який нумерує раціональні числа, тобто встановлює бієкцію між множинами раціональних і натуральних чисел. Прикладом такої побудови може бути наступний простий алгоритм. Складається нескінченна таблиця звичайних дробів, на кожній i (\displaystyle i)-ому рядку в кожному j (\displaystyle j)-ом стовпці якого розташовується дріб i j (\displaystyle (\frac (i)(j))). Для певності вважається, що рядки та стовпці цієї таблиці нумеруються з одиниці. Осередки таблиці позначаються (i, j) (\displaystyle \left(i,j\right)), де i (\displaystyle i)- номер рядка таблиці, в якій розташовується осередок, а j (\displaystyle j)- Номер стовпця.

Отримана таблиця обходиться «змійкою» за формальним алгоритмом.

Ці правила проглядаються зверху вниз і наступне положення вибирається за першим збігом.

У процесі такого обходу кожному новому раціональному числу ставиться у відповідність чергове натуральне число. Т. е. дроби 1/1 (\displaystyle 1/1)ставиться у відповідність число 1, дробу 2/1 (\displaystyle 2/1)- Число 2, і т. д. Потрібно відзначити, що нумеруються тільки нескоротні дроби. Формальною ознакою нескоротності є рівність одиниці найбільшого загального дільника чисельника та знаменника дробу.

Наслідуючи цей алгоритм, можна занумерувати всі позитивні раціональні числа. Це означає, що безліч позитивних раціональних чисел Q + (\displaystyle \mathbb (Q) _(+))счётно. Легко встановити бієкцію між множинами позитивних і негативних раціональних чисел, просто поставивши у відповідність кожному раціональному числу протилежне йому. Т. о. безліч негативних раціональних чисел Q − (\displaystyle \mathbb (Q) _(-))теж лічить. Їхнє об'єднання Q + ∪ Q − (\displaystyle \mathbb (Q) _(+)\cup \mathbb (Q) _(-))також лічимо за якістю лічильних множин. Багато ж раціональних чисел Q = Q + ∪ Q − ∪ ( 0 ) (\displaystyle \mathbb (Q) =\mathbb (Q) _(+)\cup \mathbb (Q) _(-)\cup \left\(0\right\) ))теж лічимо як об'єднання лічильної множини з кінцевим.

Зрозуміло, існують інші способи занумерувати раціональні числа. Наприклад, для цього можна скористатися такими структурами як дерево Калкіна - Вілфа, дерево Штерна - Броко або ряд Фарея.

Твердження про рахунковості безлічі раціональних чисел може викликати деяке здивування, тому що на перший погляд складається враження, що воно набагато ширше за безліч натуральних чисел. Насправді, це не так і натуральних чисел вистачає, щоб занумерувати всі раціональні.

Недостатність раціональних чисел

Якщо 2 = m n (\displaystyle (\sqrt (2))=(\frac (m)(n))), то 2 = 2 ⋅ 2 = m n ⋅ m n = m 2 n 2 (\displaystyle 2=(\sqrt (2))\cdot (\sqrt (2))=(\frac (m)(n))\cdot (\ frac (m)(n))=(\frac (m^(2))(n^(2)))), тобто . Отже, число m 2 (\displaystyle m^(2))парно, але добуток двох непарних чисел непарно, що означає, що саме число m (\displaystyle m)також парно. А значить знайдеться натуральне число k (\displaystyle k), таке що число m (\displaystyle m)можна уявити у вигляді m = 2 k (\displaystyle m=2k). Квадрат числа m (\displaystyle m)у цьому сенсі m 2 = 4 k 2 (\displaystyle m^(2)=4k^(2)), але з іншого боку m 2 = 2 n 2 (\displaystyle m^(2)=2n^(2)), значить 4 k 2 = 2 n 2 (\displaystyle 4k^(2)=2n^(2)), або n 2 = 2 k 2 (\displaystyle n^(2)=2k^(2)). Як показано раніше для числа m (\displaystyle m), це означає, що число n (\displaystyle n)- парно, як і m (\displaystyle m). Але тоді вони не є взаємно простими, тому що обидва поділяються на . Отримана суперечність доводить, що 2 (\displaystyle (\sqrt (2)))немає раціональне число.

Як ми вже бачили, безліч натуральних чисел

замкнуто щодо складання та множення, а безліч цілих чисел

замкнуто щодо складання, множення та віднімання. Однак жодна з цих множин не замкнута щодо розподілу, оскільки розподіл цілих чисел може призвести до дробів, як, наприклад, у випадках 4/3, 7/6, -2/5 і т.д. Сукупність всіх таких дробів утворює безліч раціональних чисел. Таким чином, раціональне число ( раціональний дріб) є таке число, яке можна у вигляді , де а і d - цілі числа, причому d не дорівнює нулю. Зробимо з цього приводу кілька зауважень.

1) Ми зажадали, щоб d було від нуля. Ця вимога (математично записувана нерівністю) необхідна, оскільки тут d є дільником. Розглянемо такі приклади:

Випадок 1. .

Випадок 2. .

У випадку 1 d є дільником у сенсі попереднього розділу, тобто 7 є точний дільник 21, У випадку 2 d, як і раніше, є дільником, але вже в іншому сенсі, оскільки 7 не є точним дільником 25.

Якщо 25 назвати ділимим, а 7 - дільником, ми отримаємо приватне 3 і залишок 4. Отже, дільник використовується тут у загальному сенсі і застосовно до більшої кількості випадків, ніж у гол. I. Однак у випадках, подібних до випадку 1, має залишатися застосовним поняття дільника, введене в гол. I; тому необхідно, як і гол. I виключити можливість d = 0.

2) Зазначимо, що, у той час як вирази раціональне число та раціональний дріб є синонімами, саме по собі слово дріб використовується для позначення будь-якого алгебраїчного виразу, Що складається з чисельника та знаменника, як, наприклад,

3) До визначення раціонального числа входить вираз «число, яке можна у вигляді , де а і d - цілі числа і . Чому його не можна замінити виразом «число виду , де а і d - цілі числа і причиною цього є та обставина, що існує нескінченно багато способів вираження одного і того ж дробу (наприклад, 2/3 можна також записати, як 4/6, 6 /9, або 213/33, або т. п.), і нам бажано, щоб наше визначення раціонального числа не залежало від приватного способу його вираження.

Дроб визначається таким чином, що її значення не змінюється при множенні чисельника та знаменника на одне й те саме число. Однак не завжди можна сказати, просто подивившись на цей дріб, є вона раціональною чи ні. Розглянемо, наприклад, числа

Жоден їх у обраної нами записи немає виду , де а і d - цілі числа.

Ми можемо, однак, зробити над першим дробом ряд арифметичних перетворень та отримати

Таким чином, ми приходимо до дробу, що дорівнює вихідному дробу, для якого . Число отже, раціонально, але не було б раціональним, якби визначення раціонального числа вимагало б, щоб число мало вигляд а/b, де а і b - цілі числа. У разі дробу перетворення

приводять до числа. У наступних розділах ми дізнаємося, що число не може бути представлене як відношення двох цілих чисел і, отже, воно не є раціональним або, як кажуть, ірраціональним.

4) Зазначимо, що всяке ціле число раціональне. Як ми щойно бачили, це вірно у разі числа 2. У випадку довільних цілих чисел можна, аналогічно, приписати кожному їх знаменник, рівний 1, і одержати їх уявлення як раціональних дробів.

Для початку згадаємо ті числа, які ми знаємо:

1. N – натуральні числа (числа для рахунку предметів навколишнього світу)

Якщо ми складемо два натуральні числа, то знову отримаємо натуральне число. Наприклад, n 1 + n 2 = n ∈ N 3 + 7 = 10

Віднімання може вивести нас за межі натуральних чисел.

3 - 7 = -4 ∉ N

2. Число 0 - характеристика специфічної, порожньої множини.

Наприклад, мама дала синові 200 р., усі були витрачені. У кишені залишилось 0 р.

Введення числа 0 - важлива подіяу математиці. У перекладі з латині нуль - значить "ніякий". При розв'язанні рівнянь ми намагаємось розкласти їх на множники та прирівняти їх до нуля. Наприклад,

3. Z – цілі числа (натуральні числа, негативні, нуль) Z =

Безліч натуральних чисел входить у безліч цілих чисел:

Добуток будь-яких цілих чисел буде цілим числом.

Але операція поділу вже може вивести за межі цілих чисел. Наприклад,

Q - раціональні числа (безліч цілих чисел + дроби)

Дроб виду може бути скоротливим або нескоротним. Наприклад,

Дроб нескоримий, якщо найбільший загальний дільник чисельника і знаменника є 1 (НД (m; n) = 1).

Перевага нескоротних дробів у цьому, що вони мають єдину форму записи. - це нескорима форма запису.

Кожен дріб можна подати у такому вигляді:

0,50000… = 0,5(0)

0,3333….= 0,(3)

Відповідно до цього, безліч раціональних чисел можна визначити як безліч усіх десяткових, але періодичних дробів.

Важливий перехід від звичайних дробівдо десяткових. Десятковий дріб можна отримати звичайним розподілому стовпчик. Наприклад, (рис. 1).

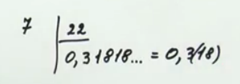
Рис. 1. Розподіл у стовпчик, отримання десяткового дробу

Це число можна уявити інакше. Нехай = 2,199999. Помножимо його на 10, тоді отримаємо 10 = 21,9999. Віднімаємо одне з іншого і отримаємо:

Висновок: якщо ми маємо число з періодом 9, його можна уявити інакше ().

Такий запис дає можливість отримати однозначність запису замість числа з періодом.

Як ми можемо записати багато раціональних чисел?

Ми можемо записати безліч раціональних чисел як безліч нескоротних дробів або як безліч десяткових дробів, кінцевих чи періодичних.

Важливою особливістю множини Q раціональних чисел є їхня замкнутість щодо операцій:

Додавання;

Віднімання;

множення;

Поділу (не на нуль);

Зведення у натуральний ступінь.

Через війну цих операцій із раціональними числами ми знову отримуємо раціональне число.

Проте вилучення кореня виводить нас межі безлічі раціональних чисел. Наприклад, . Завдяки йому ми дізнаємося, що таке ірраціональні числа, які ми розглядатимемо далі. - Ірраціональне число.

Раціональні числа досить густо заселяють числову пряму, але не заповнюють її суцільно, залишаючи місця для ірраціональних чисел.

приклад.Переконаємося, що між і існує безліч раціональних чисел на числовій прямій.