Позитивне раціональне число у вигляді десяткового дробу. Дроби, раціональні числа. Початковий рівень. Порівняння речових чисел

У практичній діяльності широко використовуються дроби, знаменники яких є ступенями 10. Їх називають десятковими.

Десятичним називається дріб виду , де т і п - натуральні числа.

Десяткові дроби прийнято записувати беззнаменника. Наприклад, дріб - записують у вигляді 3,67, а дріб - у вигляді 0,007.

З'ясуємо, як утворюється такий запис.

Нехай дано дріб, де m, nÎN. Представимо її чисельник у такому вигляді:

Тоді, за правилами дій над ступенями при , отримаємо:

Сума є записом цілого невід'ємного числа (позначимо його буквою А), а сума становить дробову частину числа, її прийнято записувати без знаменника як . Отже, дріб можна у наступному вигляді: , тобто. при записі дробу останні nцифр десяткового запису числа mвідокремлюють комою. Якщо чисельник містить менш ніж n десяткових знаків, то перед ним пишуть стільки нулів, щоб вийшла цифра, після чого відокремлюють комою nзнаків, починаючи з кінця. Наприклад,

Як відомо, порівняння десяткових дробів та арифметичні діїнад ними легко виконувати, якщо дроби мають один і той самий знаменник.

В основі приведення десяткових дробів до спільному знаменникулежить таке твердження: якщо до десяткового дробу приписати праворуч будь-яке число нулів, то вийде десятковий дріб, що дорівнює даній.

Ця властивість дозволяє наводити десяткові дробидо спільного знаменника так: якщо в одного дробу після коми стоїть nцифр, а в іншої pцифр, причому, для приведення їх до спільного знаменника достатньо до першого дробу приписати праворуч нулів. Тоді в обох дробів після коми стоятиме порівну цифр, а це означає, що вони мають один і той самий знаменник.

Користуючись цим правилом, легко виконувати порівняння десяткових дробів, так як воно зводиться до порівняння натуральних чисел: щоб порівняти два десяткові дроби, треба зрівняти в них число десяткових знаків після коми, відкинути коми і порівняти натуральні числа.

Наприклад, так як , а , тому що .

Як відомо, для дробів, що мають однакові знаменники, додавання та віднімання зводиться до відповідних операцій над їх числами. Це дозволяє звести додавання та віднімання десяткових дробів до дій над натуральними числами.

Наприклад,

Множення та розподіл десяткових дробів не вимагає приведення їх до спільного знаменника, але вони також зводяться до відповідних дій над натуральними числами.

Серед десяткових дробів виділяють і часто використовують дріб. Її називають відсоткомта позначають . Запис позначає . Наприклад, - це дріб або .

Відсотки було введено, коли не існувало десяткових дробів. Щоб проводити розрахунки за позиками, визначали приріст капіталу з розрахунку 100 грошових одиниць. Цей приріст і називали числом відсотків (pro centum – на сто).

Простота порівняння та виконання дій над десятковими дробами призводить до наступного питання: будь-який дріб виду (т, п е N) можна записати як кінцевого десяткового дробу, тобто. дробу, у якого після коми стоїть кінцева кількість цифр? Відповідь на нього дає така теорема.

Теорема.Для того щоб нескоротний дріб дорівнював десятковим, необхідно і достатньо, щоб у розкладання її знаменника пна прості множники входили лише 2 та 5.

Доведення.Нехай розкладання знаменника nна прості множники має вигляд і нехай. Тоді.

Це означає що .

Назад. Нехай, тобто . Якби в розкладанні знаменника nна прості множники входило просте число р, Відмінне від 2 і 5, то ділилося б на р. Але не поділяється на ртоді mділиться на р,і дріб можна було б скоротити на рвсупереч припущенню. Набули протиріччя.

Так, наприклад, дріб можна записати у вигляді десяткового: він нескоримий і . Дроб нескоротний, але . Оскільки до розкладання знаменника цього дробу входить множник, відмінний від 2 і 5, то дріб не можна записати у вигляді десяткового.

Дроб не можна уявити у вигляді кінцевого десяткового дробу. Але, ділячи 1 на 3, отримуємо, що . Далі знаходимо, що ; і т.д. Взагалі для будь-кого nмаємо:

Замість того, щоб писати безліч нерівностей, кажуть, що дроби відповідає нескінченний десятковий дріб . Це означає, що якщо відкинути в нескінченному дробі всі цифри, починаючи з деякого, то матимемо число, менше , а якщо в отриманому числі збільшити останню цифруна 1, буде число, більше .

Будь-який кінцевий десятковий дріб можна записати у вигляді нескінченного, приписавши до нього праворуч послідовність нулів. Наприклад, дріб 0,25 можна записати так: Тут для всіх цифр, починаючи з деякої, вийде число, що не перевищує . Наприклад, якщо залишити лише одну цифру після коми, то вийде , яке менше , а якщо залишити три цифри після коми, то буде число , що дорівнює . Якщо після відкидання збільшити останню цифру на 1, то маємо число, більше (наприклад, або ). Для стислості перший із дробів пишуть у вигляді

Доведення.Нехай раціональне число представлене нескоротним дробом. Щоб перетворити її на десяткову, треба виконати розподіл натурального числа m на натуральне число n. У цьому будуть залишки, менші n, тобто. числа виду 0, 1, 2, ... n-1. Якщо хоча б один із залишків виявиться рівним нулю, то після поділу вийде кінцевий десятковий дріб (або, що те ж саме, нескінченний десятковий дріб, що закінчується послідовністю нулів). Якщо ж всі залишки відмінні від нуля, то розподіл буде нескінченним процесом, але кількість різних залишків звичайно, і тому, починаючи з деякого кроку, якийсь залишок повториться, що призведе до повторення цифр у приватному.

Покажемо з прикладу переведення періодичних дробів у прості.

Нехай дано дріб 0. (28). Позначимо відповідне їй раціональне число через атоді а=0.282828… Домножимо обидві частини рівності на 100. Отримаємо 100 а=28.2828…, 100а=28+0.2828…, 100а=28+а, а=. Цей дріб нескоротний.

Взагалі чисто періодичний нескінченний десятковий дріб дорівнює такому звичайному дробу, чисельник якого дорівнює періоду, а знаменник складається зі стільки дев'яток, скільки цифр у періоді дробу.

Нехай даний змішано періодичний дріб 0.8(61) тобто. 0.86161.… Позначимо відповідне їй раціональне число через атоді а=0.86161.… Помноживши обидві частини цієї рівності на 10, отримаємо 10 а

Взагалі змішано періодичний дріб з нулем у цілій частині дорівнює такому звичайному дробу, чисельник якого дорівнює різниці між числом, записаним цифрами, що стоять до початку другого періоду, і числом, записаним цифрами, що стоять до початку першого періоду, а знаменник складається з такої кількості дев'яток, скільки цифр у періоді, та такого числа нулів, скільки цифр коштує до початку першого періоду.

Прості дроби

Що таке дроби? Згадуються приклади з початкової школи. Уявіть собі смачний пиріг такої, і голодної дитини. Як би так зробити, щоб пирога дісталося всім? Мабуть, треба його поділити, поділити пиріг на людину. Дивись малюнок.

На малюнку ти бачиш пиріг, що розрізає на 4 часточки. Так ось, якраз дріб – це і є частка від цілого. В даному випадку від цілого шматка осторонь відокремлена одна частка, одна з чотирьох, одна четверта. Це простий дріб. Пзростаючі дроби прийнято записувати одним з наступних способів: , Ти не повіриш, всі ці записи означають те саме – одна четверта. А що залишиться, якщо забрати цю, з, або, забрали. Мабуть, залишиться часточки, з. Запишемо, як годиться, . Можна навіть ось так:

Те, що знаходиться вище риси - це чисельник(ну або зліва від межі в такому записі як тут), те, що нижче – знаменник.

Приклади простих дробів:

У цьому ряду всі дроби правильні, у них чисельник менший за знаменник. Окрім однієї. Так-так, ти не помилився, буває і таке, що чисельник більший за знаменник, як у цьому дробі, наприклад : . Якщо чисельник більший за знаменник, то дріб називається неправильною.

Незалежно від того правильний дріб або неправильний, він буде простим. Давай зупинимося на не правильного дробу. Що це вона неправильна? Згадуй приклад із пирогом, там була одна частина з чотирьох, а тут що виходить? частин з? Нісенітниця якась! У нас у знаменнику число, яке означає, що весь пиріг складається із стільки частин! Беремо частини і повчаємо цілий рівний пиріг. Але чисельник каже, що на даний моменту нас є лише одна із цих частин. А? Що ж, у нас є частини, а для цілого пирога в цьому випадку треба частини. Ну так давай зберемо зі шматочків цілі пироги і окремо їх поставимо. Як дізнатися, скільки пирогів ми можемо отримати з частин? Мабуть, треба якраз і поділити. Якщо спробувати скласти пирогів, тобто. , Треба частин. Не вистачає. А, о, вистачило! Виходить цілих пирогів зібрали, поклали убік. Залишилося шматка. А для цілого пирога треба частини. У результаті у нас цілих і (дві треті) пирога. Багато місця займає таке позначення. А якщо прибрати зайві слова і залишити тільки (п'ять цілих і дві треті). Те, що в нас вийшло (), називають змішаний дріб- Дріб, записана у вигляді цілого числа і правильного дробу і розуміється як сума цього числа і дробу. Те, що між пирогами і пирога немає ніякого знака не говорить про те, що там знак множення, якби ми писали! Запам'ятай, між цілою та дробовою частинами можна поставити знак плюс, ось так: .

Також можна зробити і зворотний вплив, тобто. перетворення зі змішаного дробу на неправильний дріб. Ти ж знаєш, як це зробити? Звісно, ​​треба помножити знаменник дробу (у разі, знаменник дорівнює), помножити знаменник…, мабуть, і додати нецілу частину, саме – . В результаті отримаємо вихідне.

Перетвори такі неправильні дроби:

Відповіді:

Десяткові дроби

Існує ще один вид дробів, впевнений ти його знаєш. Бери калькулятор і поділи на, наприклад. Що пише, ? Що за річ така! Читається це як п'ять цілих та п'ять десятих, рівносильно. Іншими словами, все це одне й те саме. Дроби типу – все це десяткові дроби– це ті самі звичайні дроби, але в так званому десятковому записі. Десятковий записвикористовується для дробів із знаменниками, і т. д. У десяткових дробах так само є ціла та дробова частини. Для ясності візьмемо такий дроб:

• до коми – ціла частина ();
• перший знак після коми – десяті частки ();
• другий – соті частки ()
• третій – ().

І так далі. Залежно від того, на якому місці після коми знаходиться останній знак, читається число. Читається так: одна ціла, дві десятих; - сорок дві цілих, дві сотих; - нуль цілих сто двадцять дві тисячі.

Скорочення дробів

Ось тобі дріб – побачивши цей у тебе не виникає жодних думок? Гаразд, давай так, і діляться на… Так, діляться на. А що, якщо я скажу тобі, що ти можеш розділити на і розділити на, і що записати в такому вигляді як було до поділу, а саме: , а простіше кажучи, . Це ще не все, ти так само можеш помножити на, наприклад, і, а результат записати так. По суті. Все це випливає з основної властивості дробу: якщо чисельник і знаменник дробу помножити (розділити) на те саме число, дріб не зміниться. За допомогою основної властивості дробу можна замінити цей дрібінший, що дорівнює даної, але з меншими чисельником та знаменником. Така заміна називається скороченням дробу.

Спробуй скоротити дроби сам:

Відповіді:

Приведення дробів до спільного знаменника

Уявляєш, будь-які два дроби можна привести до спільного знаменника! Ну, якщо тебе це не вразило, ти, мабуть, не зрозумів, про що я. Ось дивись. Є два дроби та. Тобі треба змінити ці дроби те щоб значення дробів не змінилося, але у знаменнику в обох стало одне й те число. Підкажу лише, що для цього потрібно скористатися основною властивістю дробу. Гаразд, і бути, покажу сам: ; . Як ти бачиш у знаменнику у обох дробів, і при цьому, якщо скоротити дроби, перший на, а другий на, то вийдуть ті ж самі! Сказати, як це робиться? Так і бути, тобі сьогодні щастить, читай нижче. Для приведення дробів до спільного знаменника треба:

• знайти найменше загальне кратне знаменників цих дробів (найменший загальний знаменник);
• розділити найменший загальний знаменник на знаменники даних дробів, тобто знайти для кожного дробу додатковий множник;
• помножити чисельник та знаменники кожного дробу на його додатковий множник.

Найменшим загальним знаменником (найменше загальне кратне) цих двох дробів є, тобто найменше число, яке ділиться на і (знаменники). У цьому випадку я просто перемножив їх знаменники – помножив на, отримавши цим. Щоб зрозуміти цей момент краще, раджу звернутися до теми, там ти знайдеш, що таке найменше загальне кратне (НОК) і з чим його їдять. Далі, за основною властивістю дробу мені потрібно було помножити чисельник на те ж число, на яке я примножив знаменник, щоб отримати. У першому випадку це число у другому. І, нарешті, знайшовши для обох дробів множники, множення на які призведе до потрібного результату, я множу і чисельник та знаменник дробів на відповідні множники.

Для перетворення неправильного дробу в змішаний дрібпотрібно:

• поділити чисельник дробу на його знаменник;
• залишок від розподілу записати в чисельник знаменник залишити тим самим;
• результат від розподілу записати як цілу частину.

Потренуйся:

Відповіді:

Всі дроби перебрали, а що з ними тепер робити? - Запитаєш ти. А тут, як і скрізь у математиці, складай, віднімай, помножуй, поділи – загалом, зайнятися є чим!

Складання дробів

Найпростіший варіант, коли дроби, які треба скласти, мають однаковий знаменник. Ти ж ще не забув, що це таке, правда? Наприклад, . Згадавши приклад зі шматочками пирога, думаю, ти без проблем здогадаєшся, що якщо складати рівні часточки одного пирога, знаменник не змінюватиметься, а складаються лише чисельники. Додавання буде виглядати так: . Не складно здогадатися і як складати змішані дроби.

Окремо складаються цілі та дробові частини.:

А що, якщо знаменники у дробів різні, га? наприклад. І тут ти відразу згадуєш, що ми проходили приведення дробів до спільного знаменника, і, нарешті, стає зрозумілим, навіщо це було вчити! У цьому прикладі загальним знаменником буде число, як найменше загальне кратне чисел. . Оскільки ти тепер вмієш приводити неправильний дріб до змішаного дробу, то відкрию тобі секрет, що це не просто хороший тон, але й обов'язкова дія при спрощенні виразів, після отримання відповіді позбутися неправильних дробів.

З десятковими дробами все ще простіше. Додавання робиться, як і з звичайними числами, Тільки не забувай про кому. Ось приклад: . Я пропоную вирішувати так: найзручніше віднімати в стовпчик, розташувавши один дріб під іншим, але при цьому кома повинна стояти строго під комою незалежно від кількості знаків до і після неї.

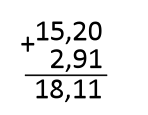
Як ти бачиш, у другого дробу після коми було на один знак більше. Для досягнення однакової кількості знаків, я додав ще один нуль наприкінці першого дробу. Неймовірно, але після останнього знака після коми ти можеш додати скільки завгодно нулів, і це не змінить сенсу дробу!

Віднімання дробів

Віднімання дробів практично ні чим не відрізняється від складання, ну хіба що знайомий. А так, віднімається знаменник із знаменника, при збереженні загального чисельника постійним, а якщо знаменники різні, дроби приводяться до спільного знаменника. Але куди ж без специфіки, тут вона теж присутня - якщо ти віднімаєш один змішаний дріб з іншого, то у випадку, якщо дробова частина дробу, що зменшується менше, ніж у того, який ти віднімаєш, то потрібно зменшити цілу частину дробу на один і перенести в дробову частину, і відняти з цілої частини цілу, та якщо з дробової дробову – щось зрозуміло хоч трішки? - Гаразд, дивись приклад, зараз розберешся!

- Як ти бачиш, в дробовій частині, тут віднімається, але, очевидно, що, не привертаючи «шматочки» від цілого пирога, віднімання зробити не можна. Для цього один пиріг ріжуть на шматки і додають до дробової частини. Виходить, що вже віднімають, а тут вже немає проблем.

А з десятковими дробами все те саме, що й було при складанні.

Ось тобі приклад:

Є питання щодо нього? Думаю, все логічно та зрозуміло, якщо ні, то ще раз подивися, як робили додавання.

Розмноження дробів

Помножувати дріб на число – елементарно! - Ось приклад, це твір чотирьох і, не плутай з - це чотири цілих, дві треті! Ну так ось, . Просто множиш число на чисельник, а знаменник не чіпаєш!

Множення змішаного дробу на число: . Примножуєш і цілу, і дробову частини. Ось як це виглядає: .

Все складніше при множенні дробу на дріб. Давай прямо по пунктиках:

• Якщо дріб змішаний, привести його до вигляду звичайного неправильного дробу;
• Перемножити чисельники дробів, перемножити знаменники дробів;
• Записати результат множення чисельників у чисельник, а знаменників у знаменник.

Зауваж, що для множення дробів з різними знаменникамине потрібно приводити їх до спільного знаменника!

Ось як усе робиться: .

Множення десяткових дробів на число або на десятковий дріб робиться просто в стовпчик, і без ком. Головне не забути, що? Правильно, після множення поставити кому, відрахувавши праворуч стільки знаків, скільки було в сумі у двох множників до множення. Наприклад: . У множниках було в сумі два знаки праворуч від коми, можна просто перемножити і, а потім до результату дописати кому, відрахувавши два знаки праворуч.

Розподіл дробів

Поділ. А що поділ? Поділ це дію зворотне множення. Зараз поясню, існує таке поняття, як зворотний дріб», або дріб зворотний даною, інакше кажучи, це просто перевернута дріб! Поділ дробу на дріб по суті це множення на дріб зворотний.

Дивись: Як ти бачиш, дріб просто перевертається, а знак розподілу змінюється на множення!

А поділ дробу на число чи навпаки особливо не відрізняється від поділу на дріб, адже будь-яке число можна уявити у вигляді дробу – як, запитаєш ти? А ти знаєш скільки буде, наприклад? Насправді це пирогів розділити на одну людину. Скільки пирогів він отримає? Сім! Таким чином, будь-яке число можна представити у вигляді дробу, в якому це число поділено на. Отже, . Поділ десяткових дробів проводиться рівно, так само як і множення, з тим же головним правилом, не забувати після поділу поставити в приватному ком, відрахувавши праворуч стільки знаків, скільки було в сумі у діленого і дільника до самого поділу!

Перетворення десяткового дробу на звичайний дріб

Бувають ситуації, коли доводиться перетворювати десятковий дріб у звичайний. Робиться це дуже просто. Давай візьмемо дріб, наприклад, запишемо його спочатку як простий дріб, у нас буде нуль цілих і чотирнадцять десятих, так і напишемо: . Але дріб неправильний, його можна скоротити, а так само перетворити на змішаний дріб: .

Раціональні числа

Раціональні числа- це цілі та дробові числа(прості дроби, кінцеві десяткові дроби та нескінченні періодичні дроби).

З простими дробамизрозуміло, а кінцевими десятковими називають дроби, у яких після коми якесь певне число знаків, навіть якщо їх багато.

А ось нескінченні періодичні дроби– це дроби з знаками, що періодично повторюються, після коми. Не всі звичайні дроби можна як кінцевої десяткової дроби. Будь-яке раціональне число можна як дроб, з чисельником що належить цілим числам, а знаменником – натуральним. Так при розподілі одного на три десятковий дріб вийде нескінченним, але знаки після коми будуть повторюватися, ... або як це ще записують, читається це як «нуль цілих і три в періоді». А буває так. Так от, періодичні десяткові дроби теж відносяться до раціональних чисел. Але не відносяться до них нескінченні неперіодичні десятковіе дроби. Це дроби типу типу , які мають нескінченну кількість знаків після коми. Такі дроби називаються ірраціональними. Ттак само до них відносяться коріння, наприклад: .

Отже, ірраціональними є:

• неперіодичні десяткові дроби;
• для будь-якого натурального, що не є точним квадратом;
• для будь-якого раціонального, де;
• для будь-якого позитивного раціонального;
• , а також для будь-якого цілого.

Раціональними будуть:

• натуральні числа;
• цілі числа;
• прості дроби;
• змішані числа;
• кінцеві та нескінченні періодичні десяткові дроби.

Приклади

Спробуй відрізни, які числа тут раціональні, а які – ні.

Відповіді:

1. Раціональне
2. Ірраціональне
3. Раціональне
4. Раціональне
5. Ірраціональне
6. Ірраціональне
7. Раціональне

Для закріплення пройденого матеріалу пропоную тобі вирішувати ще кілька прикладів.