Числа. Додавання раціональних чисел

Основні властивості дій із числами:

Перші дві властивості - це властивості додавання, наступні два - множення. П'ята властивість відноситься до обох операцій.

Нічого нового у цих властивостях немає. Вони були справедливі і для натуральних, і цілих чисел. Вони також вірні для раціональних чисел і будуть вірні для чисел, які ми вивчатимемо далі (наприклад, ірраціональних).

Перестановні властивості:, .

Від перестановки доданків чи множників результат не змінюється.

Сполучні властивості:, .

Додавання або множення кількох чисел можна робити в будь-якому порядку.

Розподільча властивість:.

Властивість пов'язує обидві операції - додавання та множення. Також якщо його читати зліва направо, його називають правилом розкриття дужок, і якщо у зворотний бік - правилом винесення загального множника за дужки.

Наступні дві властивості описують нейтральні елементидля складання та множення: додавання нуля та множення на одиницю не змінюють вихідного числа.

Ще дві властивості, які описують симетричні елементидля складання та множення, сума протилежних чисел дорівнює нулю; твір зворотних чиселодно одиниці.

Наступне якість: . Якщо число помножити на нуль, то в результаті завжди буде нуль.

Остання якість, яку ми розглянемо: .

Помноживши число , отримуємо протилежне число. Ця властивість має особливість. Решта розглянуті властивості не можна було довести, використовуючи інші. Цю ж властивість можна довести, використовуючи попередні.

Множення на

Доведемо, якщо помножити число на , то отримаємо протилежне число. Використовуємо при цьому розподільну властивість: .

Воно правильне для будь-яких чисел. Підставимо замість числа і:

Ліворуч у дужках стоїть сума взаємно протилежних чисел. Їхня сума дорівнює нулю (у нас є така властивість). Зліва тепер. Праворуч, отримуємо: .

Тепер ліворуч у нас стоїть нуль, а праворуч – сума двох чисел. Але якщо сума двох чисел дорівнює нулю, ці числа взаємно протилежні. Але у числа лише одне протилежне число: . Значить, - і є : .

Властивість доведено.

Таку властивість, яку можна довести, використовуючи попередні властивості, називають теорема

Чому тут немає властивостей віднімання та поділу? Наприклад, можна було б записати розподільну властивість для віднімання: .

Але так як:

• віднімання будь-якого числа можна еквівалентно записати у вигляді додавання, замінивши число на протилежне:

• розподіл можна записати як множення на зворотне число:

Отже, властивості складання та множення цілком можна застосовувати для віднімання та поділу. У результаті перелік якості, які потрібно запам'ятати, виходить коротше.

Усі розглянуті нами властивості є виключно властивостями раціональних чисел. Всім цим правилам підпорядковуються інші числа, наприклад, ірраціональні. Наприклад, сума та протилежного йому числа дорівнює нулю: .

Тепер ми перейдемо до практичної частини, розв'яжемо кілька прикладів.

Раціональні числа у житті

Ті властивості предметів, які ми можемо описати кількісно, ​​позначити якимось числом, називаються величинами: довжина, вага, температура, кількість.

Одну й ту саму величину можна позначити і цілим, і дрібним числом, позитивним або негативним.

Наприклад, ваш ріст м - дробове число. Але можна сказати, що він дорівнює см - це вже ціле число (рис. 1).

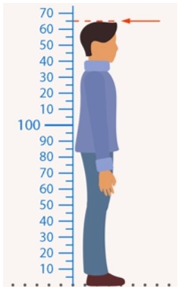
Рис. 1. Ілюстрація наприклад

Ще один приклад. Негативна температура за шкалою Цельсія буде позитивною за шкалою Кельвіна (рис. 2).

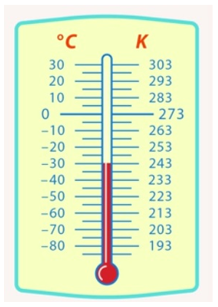
Рис. 2. Ілюстрація наприклад

При будівництві стіни будинку одна людина може виміряти ширину і висоту в метрах. У нього виходять дрібні величини. Усі обчислення далі він проводитиме з дробовими (раціональними) числами. Інша людина може все виміряти в кількості цегли в ширину та висоту. Отримавши лише цілі значення, він і обчислення проводитиме з цілими числами.

Самі величини немає ні цілими, ні дробовими, ні негативними, ні позитивними. Але число, яким ми описуємо значення величини, є цілком конкретним (наприклад, негативним і дробовим). Це залежить від шкали вимірів. І коли ми від реальних величин переходимо до математичної моделі, то працюємо з конкретним типом чисел

Почнемо зі складання. Доданки можна переставляти так, як нам зручно, і дії можна виконувати в будь-якому порядку. Якщо доданки різних знаків закінчуються на одну цифру, зручно спочатку виконувати дії з ними. Для цього поміняємо доданки місцями. Наприклад: .

Звичайні дробиз однаковими знаменникамилегко складаються.

Протилежні числа у сумі дають нуль. Числа з однаковими десятковими «хвостами» легко віднімаються. Використовуючи ці властивості, а також переміщувальний закон додавання, можна полегшити обчислення значення, наприклад, наступного виразу:

Числа з десятковими «хвістами», що доповнюють друга, легко складаються. З цілими та дробовими частинами змішаних чиселзручно працювати окремо. Використовуємо ці властивості при обчисленні значення наступного виразу:

Перейдемо до множення. Є кілька чисел, які легко перемножити. Використовуючи переміщувальну властивість, можна переставити множники так, щоб вони виявилися поруч. Кількість мінусів у творі можна порахувати одночасно і зробити висновок про знак результату.

Розглянемо такий приклад: .

Якщо із співмножників дорівнює нулю, то добуток дорівнює нулю, наприклад: .

Добуток зворотних чисел дорівнює одиниці, а множення на одиницю не змінює значення твору. Розглянемо такий приклад: .

Розглянемо приклад із застосуванням розподільної властивості. Якщо розкрити дужки, кожне множення виконується легко: .

Іноді для спрощення обчислень зручно загальний множниквинести за дужку: .

Множення на нуль дає в результаті нуль. Правильне і зворотне твердження: якщо добуток дорівнює нулю, то хоча б один із співмножників дорівнює нулю. Інакше кажучи, немає так, щоб перемножили два чи кілька чисел, не рівних нулю, й у відповіді отримали нуль. Ця властивість дозволяє легко вирішити деякі рівняння.

Вирішення деяких рівнянь

Розглянемо такі рівняння, де одна частина – це твір кількох множників, а інша – нуль.

У цьому рівнянні ліва частина – добуток трьох множників. Добуток кількох множників дорівнює нулю, якщо хоча б один із них дорівнює нулю. Прирівняємо кожен множник до нуля, отримаємо три рівняння.

При розв'язанні таких рівнянь потрібно бути обережним. Крім того, що один з множників повинен дорівнювати нулю, всі інші при цьому повинні мати сенс.

Розглянемо такий приклад: . Якщо прирівняти першу дужку до нуля, отримаємо корінь. Але при другому множнику не визначено (розподіл на нуль не визначено). Значить, немає сенсу і вся ліва частина рівняння. Виходить, що єдиним коренем рівняння буде нуль останньої дужки, тобто число .

1. Математика 5 клас. Віленкін Н.Я., Жохов В.І., Чесноков А.С., Шварцбурд С.І. М: Мнемозіна, 2013.
2. Математика 5 клас. Єріна Т.М. Робочий зошитдо підручника Віленкіна Н.Я. М: Іспит, 2013.
3. Математика 5 клас. Мерзляк А.Г., Полонський В.Б., Якір М.С., М.: Вентана – Граф, 2013.

1. School-assistant.ru ().
2. Cleverstudents.ru ().
3. Лена24.рф ().

Домашнє завдання

1. Спростіть вирази:

2. Вибравши зручний порядок обчислення, знайдіть значення виразу:

3. Знайдіть значення виразу:

— це складання цілих і дрібних позитивних і негативних чисел.

1. Додавання раціональних чисел з однаковими знаками.

Приклад:

Потрібно скласти такі раціональні числа: 0,7 та 7/8.

Перевівши задане число з десяткового дробу до звичайного, отримуємо такий вираз: 7/10+7/8 . Далі робимо складання дробів з різними знаменниками:

Коли раціональні числа, що складаються, можна записати у вигляді кінцевих десяткових дробів, або у вигляді змішаних чисел, то можна виконати складання десяткових дробів та додавання змішаних чисел.

6. Додавання негативних раціональних чисел.

Додавання негативних раціональних чисел відбувається згідно з правилами складання негативних чисел: спочатку складаємо модулі доданків і перед підсумковим числом ставиться знак мінус.

Приклад:

Потрібно скласти негативне число -4,0203 з негативним числом -12,193.

Модулі заданих чисел дорівнюють 4,0203 та 12,193 відповідно. Складаємо десяткові дробиу стовпчик:

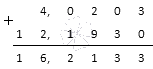
Тепер перед остаточним числом ставимо знак мінус, отримуємо −16,2133.

Ціль: узагальнити та систематизувати вміння та навички виконання дій з раціональними числами

Завдання:

1. Освітні: повторити поняття координатної прямої, раціональних чисел; правила порівняння чисел на координатній прямій, удосконалити навички додавання, віднімання, множення та поділу раціональних чисел.

2. Розвиваючі: розвивати пізнавальну активність учнів, формувати навички усної та письмової самостійної роботи, взаємоконтролю та самоконтролю, кмітливість, кмітливість.

3. Виховні: прищеплювати інтерес до математики з урахуванням загальнолюдських цінностей. Виховання волі до добра, справедливості, істини, праведної поведінки.

Обладнання: інтерактивна дошка, висловлювання Піфагора " Статую фарбує образ, а людини дії його " , картки з позитивними і негативними властивостями людини, серця різного розміру, картка мандрівника, раздаточный материал.

Цінність:праведна поведінка

Якості:працьовитість, завзятість, допитливість, самостійність, дружелюбність

План уроку:

1. Оргмомент.

2. Вступне слово вчителя.

3. Актуалізація опорних знань:

а) Елемент інтеграції математики та самопізнання:

Координатна пряма та проведення паралелі із загальнолюдськими цінностями

(робота на дошці з картками та сердечками з коментарями та відповідями учнів);

б) Розминка «Знайди помилку» (взаємоперевірка);

4. Усна самостійна робота "180 секунд" (самоперевірка з поясненням).

5. Удосконалення умінь та навичок виконання арифметичних дійіз раціональними числами. (2 варіанти за картками).

6 . Диференційована самостійна робота з перевіркою «Виріши рівняння». Роздатковий матеріал (2 варіанти).

7 . Тестовий контроль "Кодовий замок". (4 варіанти)

8. Підведення підсумків. Самооцінка знань, умінь та навичок.

9 . Рефлексія.

10. Домашнє завдання.

Хід уроку:

" Статую фарбує вигляд, а людини дії його " .

1. Оргмомент.Перевірити готовність до уроку.

2. Вступне слово вчителя.

Здрастуйте, хлопці. Давньогрецький вчений Піфагор, який жив у VI – V ст. до нашої ери сказав: «Статую фарбує вигляд, а людину діяння його». Важко не погодитись зі словами великого мудреця. І нехай ці слова послужать девізом сьогоднішнього уроку – подорожі в країну позитивних та негативних чисел, де ви покажете свої найкращі якості: працьовитість, завзятість, допитливість, самостійність, дружелюбність та багато інших.

А урок наш буде присвячений правилам дій із дивовижними числами. Недарма наші пращури ставилися до них з особливим почуттям: одні – з недовірою, інші з цікавістю. В стародавньої Греціїїх називали хибними, а Індії «боргами», на відміну з інших чисел – їм протилежних – «майнов». Ви, звичайно, здогадалися, про які числа йдеться. (Про позитивні і негативні). Правильно.

Запишіть дату та тему уроку «Раціональні числа».

3. Актуалізація опорних знань.

а) Які числа називаються раціональними? Де їх можна показати? (На координатній прямій). Які числа та де відзначаються на координатній прямій? Яким є число 0? Який напрямок показує стрілка координатної осі? Як порівняти числа на координатній прямій? Сформулюйте правила складання, множення та розподілу раціональних чисел.

Поряд з позитивними та негативними числамиє поняття позитивних та негативних якостей людини. Як ви думаєте? Чи можна провести відповідність між позитивними та негативними числами та якостями людини? У вас на парті лежить лист із координатною віссю (2 учні працюють біля дошки). Подумайте і поставте у відповідність раціональним числам позитивні та негативні якості людини.

А що означає число 0 для людини на цій прямій? Як ви думаєте?

Що ви можете сказати про частину прямої якості, яка знаходиться вище нуля? Чи змінюється людина з просуванням нагору, тобто. збільшуючи кількість хороших якостей. Як? І як змінюється людина, рухаючись вниз? Коли кажуть, що людина має «велике серце»?

Який висновок можна зробити?

Який сенс містить у собі висловлювання Піфагора, яке ми привели на початку уроку?

Отже, подорож до країни Раціональних чисел» починається. Для цього вам знадобиться картка мандрівника, на якій ви запишите своє прізвище та ім'я. Тут же є маршрут нашої подорожі. На нашому шляху буде місто «Знаєк». Потім, перейшовши через річку, ми потрапимо до міста «Мудреців», де на вас чекають випробування. Останнім на нашому шляху буде місто «Майстрів», на вулицях якого ви продемонструєте свої знання, вміння та навички на цю тему.

Я бажаю вам приємної подорожі та успішного виконання всіх завдань.

б) Відомо, що кожен мандрівник має бути сміливим, спритним, винахідливим. Перевіримо, наскільки добре ви підготувалися до подорожі. Я пропоную вам перше випробування - "Знайди помилку". Якщо ви вважаєте, що приклад вирішено, то, у свою картку на етапі «розминка» поставте знак «+», якщо неправильно – знак «-».

0,6 · 4 = - 2,4 Дорогу

6 · (-0,3) = 0,18 Математика

1,5 · 2 = - 3 Здолає

3 · (- 0,6) = - 1,8 Гімнастика

=4 Розуму

= 1 Хто йде

Підряд прочитайте слова, напроти яких поставили "+". Повинне вийде висловлювання "Дорогу здолає той, хто йде".Який сенс несе у собі воно?

Діти, поміняйтеся картками. Перевірте, якщо ваш товариш правильно відповів на запитання, його відповідь ви обводите в гурток. А тепер підрахуйте скільки вірних відповідей у ​​вашого сусіда і поставте в його картку загальну кількість балів за розминку. (мах 3 бали)

4. Жодна подорож не обходиться без пригод. У житті кожної людини є моменти, коли необхідно прийняти швидке та правильне рішення. Для цього треба бути уважним та мати «багаж» знань. Зараз ми перевіримо вашу кмітливість під час виконання самостійної усної роботи «180 секунд». Перед вами 6 завдань, виконання кожного з яких відводиться 30 секунд.

Самостійна робота у місті «Знаєк» – 180 секунд. (усно)

1. -200, ...,200. Учень записав усі цілі числа від – 200 до 200 включно. Потім їх перерахував, і йому вийшло 400. А у вас? (401)

2. □ + □ + □ = - 5. Дано три числа, два з них протилежні.

Знайдіть третє число, якщо їхня сума дорівнює «-5». (−5)

3. – 9 – () = 9. Знайдіть число, яке треба відняти з «-9», щоб вийшло 9.(−18)

4. (-1) ∙ … ∙ (-5). Перемножимо всі цілі числа від «-1» до

"- 5" включно. Чи буде отримане число більшим за 50? (ні, воно 0)

5. (-12) * (-4). Між цими числами постав такий знак дії, щоб у результаті вийшло найбільше можливе число. (множення)

6. a ∙ b > 0 Чи можна знайти два числа, добуток яких позитивний, a + b<0 а сумма отрицательна?(два отрицательных числа)

А тепер, хлопці, виконаємо перевірку. (Фронтальне опитування з поясненням рішення). Поставте до своєї картки загальну кількість балів за цю роботу. (мах 6 балів)

5. "Перехід через річку"А ми вирушаємо далі. Але на нашому шляху річка. І перейде її той, хто впорається із завданням:

1 варіант	2 варіант
б) 0,6+(-2)+1,4 в) -8 · (- 0,7) г) 48,1: (‒ 48,1)	б) 0,75 - 3 + 2,25 г)-270: (‒ 9)

Працюємо біля дошки та у зошитах одночасно у двох варіантах. (Завдання оцінюється в 1 бал).

6. Подорож триває у місті «Мудреців». Вам необхідно

вибрати для вирішення одне з трьох рівнянь, виділених різним кольором. Ви самі визначаєте рівень складності. Якщо ви правильно вирішите 1-е рівняння (у першій колонці), то заробите 1 бал, якщо ви правильно вирішите 2-е рівняння (у другій колонці), то 2 бали, а 3-е рівняння (у третій колонці) - 3 бали. Хай щастить.

Місто «Мудреців»

Розв'яжи рівняння (варіант 1)

1, 4 х = - 5,6	х = -	х + 3 = -
х = - 5,6: (- 1,4) х = - 56: (- 14)	х = - : х = - ·	х = - – 3 х = ‒ х = - : х = - ·

Розв'яжи рівняння (варіант 2)

4,2 х = - 12,6	х = -	5/21х + 2 = 43/14
х = - 12,6: (- 4,2) х = - 126: (- 42)	х = - : х = - ∙	х = – 2 х = х = ( ) х = ( ) х = -

7. Останній етап нашої подорожі – місто «Майстерів». «Кодовий замок».

Але потрапити туди ми зможемо, якщо відгадаємо код замку, що висить на брамі цього міста. Я загадаю вам три загадки-питання, до кожного з яких пропонується три варіанти відповідей. Ви повинні вибрати один із них і показати мені номер із відповідною цифрою 1; 2 чи 3.

Будьте уважні та обережні: знайдіть два числа, якщо відомо, що

А) їхній добуток дорівнює 10, а сума 7

1) 1 та 10 2) – 5 та – 2 3) 5 та 2

Б) їхній добуток дорівнює 12, а сума – 7

1) – 4 та – 3 2) 4 та 3 3) – 2 та – 6

В) їх добуток дорівнює – 6, а сума 1

1) – 3 та 2 2) 3 та – 2 3) 3 та 2.

(На дошці з'являється код 312 )

Відчинилися двері міста. Ми опинилися серед майстрів: тепер ми вміємо виконувати всі дії з раціональними числами. І тепер свою майстерність та знання на тему «Арифметичні дії з раціональними числами» ви покажете при виконанні тесту.

Поспішайте робити добро людям.

8. Підсумок.

Настав час підбиття підсумків. Підрахуйте будь-ласка загальну кількість балів та поставте собі самооцінку, використовуючи критерій оцінювання:

«5» -19-21 балів

«4» -14-19 балів

«3» -9-13 балів

9. Рефлексія.

Ваші знання дуже допомогли вам сьогодні у подорожі країною «Дій з раціональними числами». Мені як екскурсоводу було приємно подорожувати разом з вами, і я хочу кожного з вас похвалити за хорошу роботу на уроці.

Хочеться відзначити, окрім знань, і вашу відповідальність, дисципліну, уміння слухати товаришів. Все це допомогло успішній подорожі. А які ще якості допомагають подолання труднощів на шляху пізнання нового? (Хлопці перераховують).

Слайд "Хмара зі слів".

Давайте ще раз звернемося до слів Піфагора. (хором). Нехай вони стануть нашим девізом, життєвим кредо.

1. Домашнє завдання:

Намалюйте будь-ласка малюнки нашої подорожі, напишіть казки, вірші про негативні та позитивні числа та дії з ними, складіть кросворди.

Дякую за урок!

Прощаючись з вами, мені хочеться дізнатися про вашу думку про урок. Виберіть одну з карток і покладіть мені в коробочку "+", якщо урок вам сподобався, "-" якщо не сподобався.

Раціональних чисел має переміщувальні та поєднувальні властивості.

Іншими словами, якщо a, b і с - будь-які , то + b = b + a, а + (b + с) = (а + b) + с.

Додавання нуля не змінює числа, а сума протилежних чисел дорівнює нулю.

Отже, будь-якого раціонального числа маємо: а + 0 = а, а + (- а)=0.

Множення раціональних чисел теж має переміщувальну і сполучну властивості. Іншими словами, якщо а, b і с – будь-які раціональні числа, то ab – ba, a(bc) – (ab)c.

Множення на 1 не змінює оптимального числа, а добуток числа на зворотне йому число одно 1.

Отже, для будь-якого раціонального числа маємо:

Розмноження числа на нуль дає у творі нуль, тобто для будь-якого раціонального числа а маємо:
а 0 = 0.
Твір може бути рівним нулю лише в тому випадку, коли хоча б один з множників дорівнює нулю: якщо а b = 0, то або а = 0, або b = 0 (може статися, що і а = 0, і b = 0) .

Множення раціональних чисел має і розподільну властивість щодо додавання. Іншими словами, для будь-яких раціональних чисел a, b і маємо: (a+b) c = ac+bc.

З раціональними числами люди, як ви знаєте, поступово знайомилися. Спочатку за рахунку предметів з'явилися натуральні числа. Спочатку їх було небагато. Так, ще недавно у тубільців островів у Торресовій протоці (що відокремлює Нову Гвінею від Австралії) були в мові назви лише двох чисел: «урапун» (один) та «наказу» (два). Островітяни вважали так: «Оказа-урапун» (три), «Оказа-Оказа» (чотири) і т. д. Всі числа, починаючи з семи, тубільці називали словом, що позначало «багато».

Вчені вважають, що слово для позначення сотні з'явилося понад 7000 років тому, для позначення тисячі – 6000 років тому, а 5000 років тому у Стародавньому Єгипті та в Стародавньому Вавилоні з'являються назви для величезних чисел – до мільйона. Але довгий час натуральний ряд чисел вважався кінцевим: люди думали, що є найбільше число.

Найбільший давньогрецький математик і фізик Архімед (287-212 рр. до н. е.) вигадав спосіб опису величезних чисел. Найбільше, яке вмів називати Архімед, було настільки велике, що для його цифрового запису знадобилася б стрічка в дві тисячі разів довша, ніж відстань від Землі до Сонця.

Але записувати такі величезні числа ще не вміли. Це стало можливим лише після того, як індійськими математиками у VI ст. була придумана цифра нуль і нею стали означати відсутність одиниць у розрядах десяткового запису числа.

При розділі видобутку й надалі при вимірах величин, та й інших схожих випадках люди зустрілися з необхідністю запровадити «ламані числа» - звичайні дроби. Події над дробами ще в середні віки вважалися найскладнішою галуззю математики. Досі німці говорять про людину, яка потрапила у скрутне становище, що вона «потрапила в дроби».

Щоб полегшити події з дробами, були придумані десяткові дроби. У Європі їх запровадив у Х585 р. голландський математик та інженер Симон Стевін.

Негативні числа виникли пізніше, ніж дроби. Довгий час такі числа вважали «неіснуючими», «хибними» насамперед через те, що прийняте тлумачення для позитивних і негативних чисел «майно - борг» призводило до подиву: можна скласти або відняти «майна» або «борги», але як розуміти твір чи приватне «майно» та «борг»?

Проте незважаючи на такі сумніви та здивування, правила множення та поділу позитивних та негативних чисел були запропоновані у III ст. грецьким математиком Діофантом (у вигляді: «Віднімання, помножене на додається, дає віднімається; віднімається на віднімається дає додається» і т. д.), а пізніше індійський математик Б хаскара (XII ст.) висловив ті ж правила у поняттях «майно», «борг» («Виробництво двох майна або двох боргів є майно; твір майна та боргу є борг». Те саме правило і при розподілі).

Було встановлено, що властивості дій над негативними числами ті ж, що і над позитивними (наприклад, і множення мають переміщувальну властивість). І, нарешті, з початку минулого століття негативні числа стали рівноправними з позитивними.

Надалі в математиці з'явилися нові числа – ірраціональні, комплексні та інші. Про них ви дізнаєтесь у старших класах.