Перетворення виразів. Початковий рівень. Винесення загального множника за дужки

Додавання та віднімання дробів Чому дорівнює площа заштрихованої фігури, якщо завдання ЗФТШ МФТІ Знайти довжину відрізка MN, який ділить площу трапеції навпіл. Зміна знаку членів дробу. Шкільна математика Дроби Складання та віднімання дробів. Виникає плутанина із знаками: де ставити мінус, а де – плюс. Ця проблема теж вирішується дуже просто. Досить, що мінус перед знаком дробу завжди можна перенести в чисельник - і навпаки. Значення дробу не зміниться, якщо змінити знак у одного з членів дробу і перед дробом: Це правило застосовується і при діях з дробами. Як надрукувати дроб: як позначити знак дробу. Відповіді ЄДІ: Якщо перед дробом поставити знак мінус, то він впливатиме і на чисельник Знак "-" перед дробом можна внести або в чисельник, або в знаменник, але не туди і туди (інакше це буде вже 2 знаки мінус, тобто .в результаті - плюс). Знак «мінус» у дробах #math Поділ негативних чисел Під час запису негативних дробів знак «мінус» можна ставити перед дробом, переносити його з чисельника в знаменник або з знаменника в чисельник. Зміна знаків у чисельнику та знаменнику дробу Предмети Алгебра 8 клас значення дробу не зміниться, якщо змінити знаки на протилежні – у чисельника та знаменника дробу 2). - змінено знак у чисельнику та перед дробом. Перед п'ятьма дробами розставлені знаки – дивіться як. Громадянин А поклав на початку року деяку суму грошей до банку під 10% річних. Наприкінці року після нарахування відсотків він зняв чверть початкової суми. Через рік після нарахування відсотків він зняв ще чверть первісної суми. І так він чинив щороку. Через скільки років (після нарахування відсотків) у нього на рахунку виявиться менше, ніж чверть первісної суми. Знайти найменше значення функції. Перераховані умови, які необхідно забезпечити, якщо учень приходить до репетитора додому. Розв'язати рівняння. Знайдіть коріння, яке належить проміжку. Біля сфери радіуса R описана правильна чотирикутна усічена піраміда, сторона нижньої основи якої в 2 рази більша за сторону верхньої основи. Знайдіть площу бічної грані піраміди; мінімально можливу площу перерізу піраміди площиною, яка проходить через діагональ нижньої основи та перетинає верхню основу піраміди. Розв'яжіть нерівність. Прямокутний трикутник АВС розташований щодо трьох концентричних кіл К1, К2 і К3 радіусів 3, 5 і 6 так, що: 1) гіпотенуза АВ є хордою К2 і стосується кола К1; 2) вершина З належить колу К3. а) Знайти площу трикутника АВС. б) Довести, що центр кіл і вершина З лежать по різні боки від гіпотенузи. За яких значень параметра р дотична до графіка функції у точці x = p не перетне графіки функцій? Як стати репетитором. Частина 1. Якщо учень приходить до репетитора додому. Перед дробами розставлені знаки, або +, або -. Наприклад, так. Позначимо одержане число через S. Чи може S = 0,45? Чи може S = 1? Знайти найменше значення | S-1 | за всіх можливих S . Єдиний державний іспит з МАТЕМАТИКИ Тренувальний варіант № 188 Профільний рівень МАТЕМАТИКА

Продовжуємо розбиратися з основами алгебри і в даному уроці ми трохи пограємося з розподільним законом множення, а саме розглянемо таку дію, як винесення загального множника за дужки.

Зміст уроку

Основний принцип

Розподільний закон множення, як ми пам'ятаємо, дозволяє помножити число на суму (або суму на число). Наприклад, щоб знайти значення виразу 3×(4+5) можна помножити число 3 на кожне доданок у дужках і скласти отримані результати:

Число 3 і вираз у дужках можна поміняти місцями (це випливає з переміщувального закону множення). У цьому випадку, кожне доданок яке в дужках, множиться на число 3:

(4 + 5) × 3 = 4 × 3 + 5 × 3 = 12 + 15

Ну і неважко здогадатися, що виходить в результаті вираз 12 +15 і 27.

Поки що не будемо обчислювати конструкцію 3×4+3×5 та складати отримані результати 12 та 15. Залишимо вираз у наступному вигляді 3 (4+5)=3×4+3×5. Нижче воно нам знадобиться таким, щоб зрозуміти суть винесення загального множника за дужки.

Розподільний закон множення іноді називають внесенням множника всередину дужок. В принципі це логічно. У виразі 3×(4+5) множник 3 був за дужками. Помноживши його на кожен доданок у дужках, ми по суті внесли його всередину дужок. Для наочності можна так і записати, хоча у школах та у ВНЗ записувати це не прийнято:

3 (4 + 5) = (3 × 4 + 3 × 5)

Оскільки у виразі 3×(4+5) число 3 множиться на кожен доданок у дужках, ця трійка є загальним множником для цих доданків.

Як говорилося вище, помноживши цей загальний множник на кожен доданок у дужках, ми вносимо його всередину дужок. Але можливий і зворотний процес - загальний множник можна винести за дужки. У даному випадку, у виразі 3×4+3×5 загальний множник видно як на долоні – це множник 3 . Його треба винести за дужки. Для цього спочатку записується сам множник.

і поруч у дужках записується вираз 3×4+3×5 але вже без загального множника 3 тому, що він винесений за дужки

3 (4+5)

Таким чином, в результаті винесення загального множника за дужки у виразі 3×4+3×5 виходить вираз 3 (4+5). Цей вираз тотожно дорівнює попередньому виразу 3×4+3×5

3×4+3×5 = 3 (4+5)

Якщо обчислити обидві частини набутої рівності, то ми отримаємо тотожність:

3×4+3×5 = 3 (4+5)

12 + 15 = 12 + 15

Як це працює

Винесення загального множника за дужки насправді є зворотною операцією внесення загального множника всередину дужок.

Якщо при внесенні загального множника всередину дужок, ми множимо цей множник на кожен доданок у дужках, то при винесенні цього множника назад за дужки ми повинні розділити кожен доданок у дужках на цей множник.

Насправді, у виразі 3×4+3×5, яке було розглянуто вище, так і відбувалося. Кожний доданок був поділений на загальний множник 3 . У нашому випадку твори 3×4 і 3×5 є складовими, тому що якщо їх обчислити, ми отримаємо суму 12+15

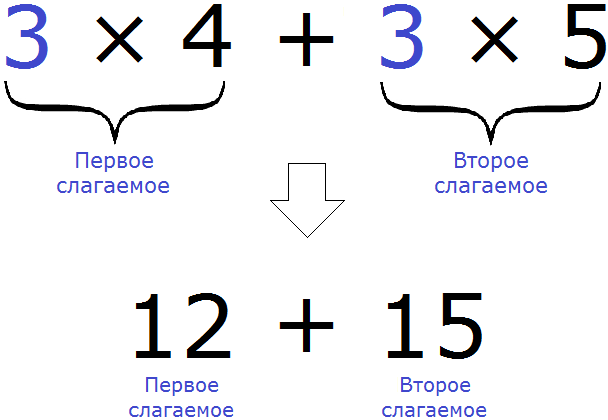
Отже, тепер ми можемо детально побачити, як відбувається винесення загального множника за дужки:

Видно, що загальний множник 3 спочатку винесений за дужки, потім у дужках відбувається розподіл кожного доданку на цей загальний множник.

Розподіл кожного доданку на загальний множник можна виконувати не тільки розділяючи чисельник на знаменник, як це було показано вище, але й скорочуючи ці дроби. В обох випадках вийде той самий результат:

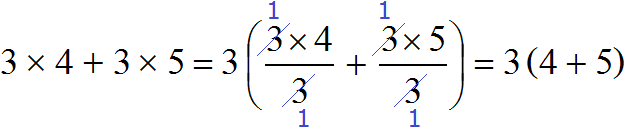
Ми розглянули найпростіший приклад винесення загального множника за дужки, аби зрозуміти основний принцип.

Але не все так просто, як здається на перший погляд. Після того, як число помножено на кожен доданок у дужках, отримані результати складають, і загальний множник зникає.

Повернемося до прикладу 3 (4+5). Застосуємо розподільний закон множення, тобто помножимо число 3 на кожне доданок у дужках і складемо отримані результати:

3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15

Після того, як обчислена конструкція 3×4+3×5, ми отримуємо новий вираз 12+15. Бачимо, що загальний множник 3 зник з поля зору. Тепер у отриманому виразі 12+15 спробуємо назад винести загальний множник за дужки, але щоб винести цей загальний множник спочатку потрібно знайти.

Зазвичай під час вирішення завдань зустрічаються саме такі висловлювання, у яких загальний множник спочатку потрібно знайти, як його виносити.

Для знаходження загального множника для доданків 12 і 15 потрібно знайти найбільший загальний дільник (НД) цих доданків. Знайдений НОД і буде спільним множником.

Отже, знайдемо НОД для чисел 12 і 15. Нагадаємо, що для того, щоб знайти НОД двох чисел, можна розкласти ці числа на прості множники, потім виписати перше розкладання і прибрати з нього множники, які не входять до розкладання другого числа. Множники, що залишилися, потрібно перемножити і отримати шуканий НОД. Якщо ви відчуваєте труднощі на цьому моменті, обов'язково повторіть .

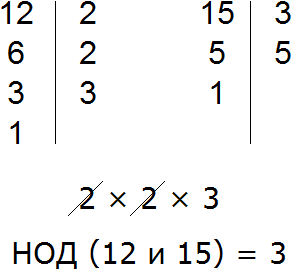
НОД для 12 та 15 це число 3. Це числоє загальним множником для доданків 12 і 15. Його потрібно виносити за дужки. Для цього спочатку записуємо сам множник 3 і поруч у дужках записуємо новий вираз, в якому кожне доданок вирази 12+15 розділено на загальний множник 3

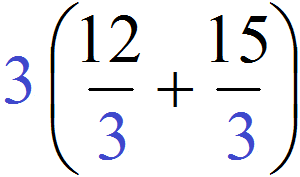
Ну і подальше обчислення не складає особливих труднощів. Вираз у дужках легко обчислюється - дванадцять поділити на три буде чотири, а п'ятнадцять поділити на три буде п'ять:

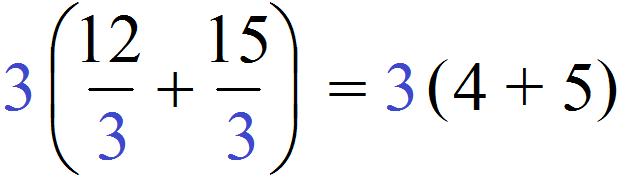
Таким чином, при винесенні загального множника за дужки у виразі 12+15 виходить 3(4+5). Докладне рішення виглядає так:

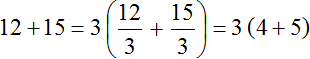
У короткому рішенні пропускається запис у якій показано, як кожен доданок розділений на загальний множник:

приклад 2. 15+20

Знайдемо НОД для доданків 15 та 20

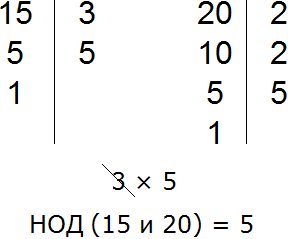
НОД для 15 і 20 це число 5. Це число є загальним множником для доданків 15 і 20. Його і винесемо за дужки:

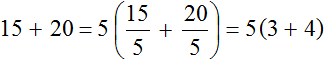
Отримали вираз 5(3+4). Вираз, що вийшов, можна перевірити на правильність. Для цього достатньо помножити п'ятірку на кожен доданок у дужках. Якщо ми все зробили правильно, то маємо отримати вираз 15+20

Приклад 3.Винести загальний множник за дужки у виразі 18+24+36

Знайдемо НОД для доданків 18, 24 і 36. Нагадаємо, що для того, щоб знайти НОД для кількох чисел, потрібно розкласти ці числа на прості множники, потім знайти добуток загальних множників:

НОД для 18, 24 і 36 це число 6. Це число є загальним множником для доданків 18, 24 і 36. Його і винесемо за дужки:

Перевіримо на правильність вираз, що вийшов. Для цього помножимо шістку на кожне доданок у дужках. Якщо ми все зробили правильно, то маємо отримати вираз 18+24+36

Приклад 4.Винести загальний множник за дужки у виразі 13+5

Доданки 13 та 5 є простими числами. Вони розкладаються тільки на одиницю та самих себе:

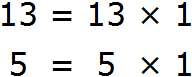
Це означає, що у доданків 13 і 5 немає загальних множників, крім одиниці. Відповідно, немає сенсу виносити цю одиницю за дужки, оскільки це нічого не дасть. Дивіться самі:

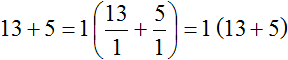
Приклад 5.Винести загальний множник за дужки у виразі 195+156+260

Знайдемо НОД для доданків 195, 156 та 260

НОД для 195, 156 і 260 це число 13. Це число є загальним множником для доданків 195, 156 і 260. Його і винесемо за дужки:

Перевіримо на правильність вираз, що вийшов. Для цього помножимо 13 на кожен доданок у дужках. Якщо ми все зробили правильно, то маємо отримати вираз 195+156+260

Вираз у якому потрібно винести загальний множник за дужки може бути не лише сумою чисел, а й різницею. Наприклад, винесемо загальний множник за дужки у виразі 16-12-4. Найбільшим загальним дільником для чисел 16, 12 і 4 це число 4. Це число і винесемо за дужки:

Перевіримо на правильність вираз, що вийшов. Для цього помножимо четвірку на кожну кількість у дужках. Якщо ми все зробили правильно, то маємо отримати вираз 16-12-4

Приклад 6.Винести загальний множник за дужки у виразі 72+96-120

Знайдемо НОД для чисел 72, 96 та 120

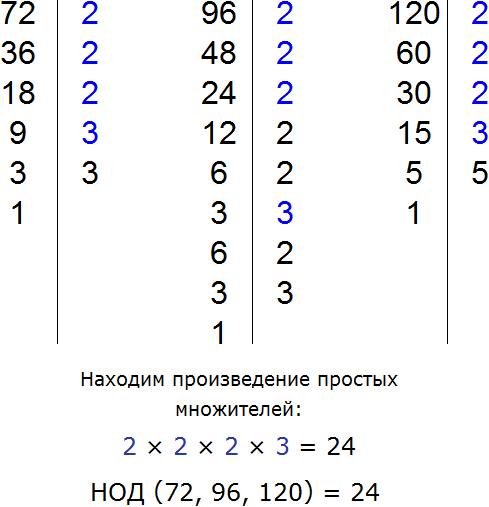
НОД для 72, 96 і 120 це число 24. Це число є загальним множником для доданків 195, 156 і 260. Його і винесемо за дужки:

Перевіримо на правильність вираз, що вийшов. Для цього помножимо 24 на кожне число у дужках. Якщо ми все зробили правильно, то маємо отримати вираз 72+96−120

Загальний множник, що виноситься за дужки, може бути і негативним. Наприклад, винесемо загальний множник за дужки у виразі −6−3. Винести загальний множник за дужки у такому вираженні можна двома способами. Розглянемо кожен із них.

Спосіб 1.

Замінимо віднімання додаванням. Нагадаємо, що для цього потрібно до зменшуваного додати число, протилежне віднімається:

Тепер знаходимо спільний множник. Спільним множником даного виразу буде найбільший спільний дільник доданків −6 та −3.

Модуль першого доданку це 6. А модуль другого доданку це 3. НОД(6 і 3) дорівнює 3. Дане число є загальним множником для доданків 6 і 3. Його і винесемо за дужки:

Легко помітити, що вираз отриманий таким чином, вийшов громіздким і не дуже красивим - багато дужок та негативних чисел не надають виразу простоти. Тому можна скористатися другим способом, суть якого полягає в тому, щоб винести за дужки не 3, а −3.

Спосіб 2.

Як і минулого разу замінюємо віднімання додаванням

Спільним множником для чисел −6 та (−3) як ми пам'ятаємо було число 3. Але цього разу ми винесемо за дужки не 3, а −3

Вираз отриманий цього разу виглядає набагато простіше та красивіше. Запишемо рішення коротше, щоб зробити його ще простіше:

Дозволяти виносити негативний множник за дужки пов'язано з тим, що розкладання чисел −6 та (−3) можна записати двома видами: спочатку зробити множину негативним, а множник позитивним:

−2 × 3 = −6

−1 × 3 = −3

у другому випадку множимо можна зробити позитивним, а множник негативним:

2 × (−3) = −6

1 × (−3) = −3

Отже ми вільні виносити за дужки той співмножник, який захочемо. Головне, щоб зрештою виходило тотожність.

Приклад 8.Винести загальний множник за дужки у виразі −20−16−2

Замінимо віднімання додаванням

−20−16−2 = −20 + (−16) + (−2)

Найбільшим спільним дільником для доданків −20, −16 та −2 є число 2. Це число є загальним множником для цих доданків. Подивимося як це виглядає:

−10 × 2 = −20

−8 × 2 = −16

−1 × 2 = −2

Але наведені розкладання можна замінити на тотожні рівні розкладання. Відмінність буде в тому, що загальним множником буде не 2, а −2

10 × (−2) = −20

8 × (−2) = −16

1 × (−2) = −2

Тому для зручності за дужки можна винести не 2 , а −2

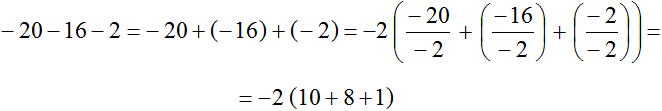
Запишемо наведене рішення коротше:

А якби винесли за дужки, то вийшло б не зовсім акуратне вираження:

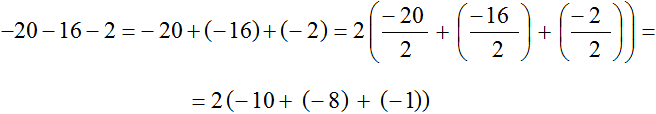
Приклад 9.Винести загальний множник за дужки у виразі −30+36−42

Замінимо віднімання додаванням

−30+16 +(−42)

Найбільшим загальним дільником доданків -30, 36 і -42 це число 6. Дане число є загальним множником для цих доданків. Але за дужки ми винесемо не 6, а −6 оскільки числа −30, 36 та −42 можна уявити як

5 × (−6) = −30

6 × (−6) = 36

7 × (−6) = −42

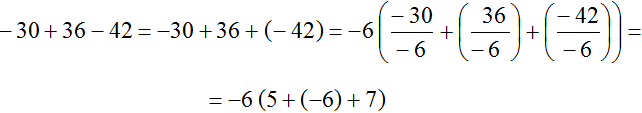
Винесення мінуса за дужки

При вирішенні завдань іноді може бути корисним винесення мінусу за дужки. Це дозволяє спростити вираз і привести його до ладу.

Розглянемо наступний приклад. Винести мінус за дужки у виразі −15+(−5)+(−3)

Для наочності укладемо цей вираз у дужки, адже йдеться про те, щоб винести мінус за ці дужки.

(−15 + (−5) + (−3))

Отже, щоб винести мінус за дужки, потрібно записати перед дужками мінус і в дужках записати всі доданки, але з протилежними знаками

Ми винесли мінус за дужки у виразі −15+(−5)+(−3) та отримали −(15+5+3). Обидва вирази рівні тому самому значенню −23

−15 + (−5) + (−3) = −23

−(15 + 5 + 3) = −(23) = −23

Тому між виразами −15+(−5)+(−3) та −(15+5+3) можна поставити знак рівності, тому що вони несуть одне й те саме значення:

−15 + (−5) + (−3) = −(15 + 5 + 3)

Насправді при винесенні мінуса за дужки знову ж таки спрацьовує розподільчий закон множення:

a(b+c) = ab + ac

Якщо поміняти місцями ліву та праву частину цієї тотожності, то вийде, що співмножник aвинесено за дужки

ab + ac = a(b+c)

Те саме відбувається, коли ми виносимо загальний множник в інших виразах і коли виносимо мінус за дужки.

Вочевидь, що з винесенні мінуса за дужки, виноситься не мінус, а мінус одиниця. Ми вже казали, що коефіцієнт 1 (як і –1) не записують.

Тому і утворюється перед дужками мінус, а знаки доданків, які були в дужках, змінюють свій знак на протилежний, тому що кожен доданок розділений на мінус одиницю.

Повернемося до попереднього прикладу та детально побачимо, як насправді мінус виносився за дужки

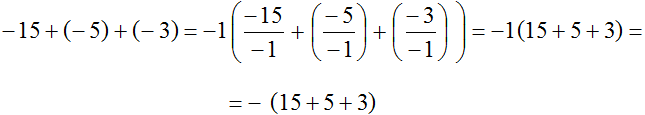
приклад 2.Винести мінус за дужки у виразі −3+5+11

Ставимо мінус і поруч у дужках записуємо вираз −3+5+11 із протилежним знаком у кожного доданка:

−3 + 5 + 11 = −(3 − 5 − 11)

Як і в минулому прикладі, насправді тут за дужки винесений не мінус, а мінус одиниця. Докладне рішення виглядає як

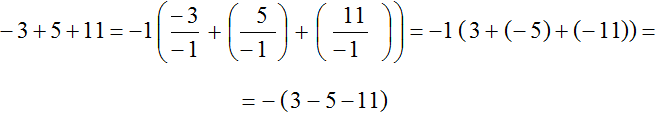
Спочатку вийшло вираз −1(3+(−5)+(−11)), але ми розкрили у ньому внутрішні дужки та отримали вираз −(3−5−11). Розкриття дужок це тема наступного уроку, тому якщо цей приклад викликає у вас труднощі, можете поки що пропустити його.

Винесення загального множника за дужки у літерному виразі

Виносити загальний множник за дужки в буквальному вираженні набагато цікавіше. Нехай вас не зупиняє те, що спочатку ви будете припускатися помилок.

Для початку розглянемо найпростіший приклад. Нехай є вираз 3a +2a. Винесемо загальний множник за дужки.

В даному випадку, загальний множник видно неозброєним оком – це множник a. Його й винесемо за дужки. Для цього записуємо сам множник aі поруч у дужках записуємо вираз 3a +2a, але вже без множника aоскільки він винесений за дужки:

Як і у випадку з числовим виразом, тут відбувається розподіл кожного доданка на загальний множник. Виглядає так:

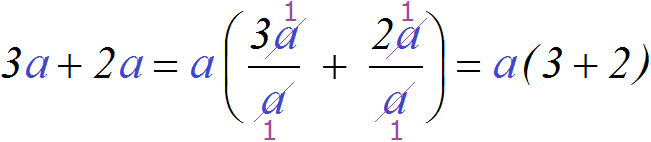
Змінні aбули скорочені на a,тобто в чисельнику та у знаменнику змінна абула поділена a .

У початківців часто виникає питання, чому при скороченні однакових змінних, виходить одиниця. Все дуже просто. Замість змінної aможе стояти будь-яке число. Ця змінна знаходиться і в чисельнику, і в знаменнику. А якщо в чисельнику та у знаменнику стоять однакові числа, то найбільший спільний дільник їм буде саме це число.

Наприклад, якщо замість змінної aпідставити число 4 , то конструкція набуде наступного вигляду: 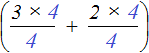. Тоді четвірки в обох дробах можна буде скоротити на 4:

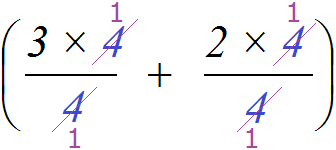
Виходить те саме, що й раніше, коли замість четвірок стояла змінна a .

Тому не слід вставати в ступор побачивши скорочення змінних. Змінна це повноправний множник, нехай навіть виражений буквою. Такий множник можна виносити за дужки, скорочувати та виконувати інші дії, які допустимі до звичайних чисел.

Букве вираз як ми пам'ятаємо містить не тільки числа, а й літери (змінні). Тому загальний множник, який виноситься за дужки часто буває літерним множником, що складається з числа та літери (коефіцієнта та змінної). Наприклад, такі вирази є буквеними множниками:

3a, 6b, 7ab, a, b, c

Перед тим, як виносити такий множник за дужки, потрібно визначитися, яке число буде в числовій частині загального множника і яка змінна буде в літерній частині загального множника. Інакше кажучи, необхідно з'ясувати який коефіцієнт буде в загального множника і яка змінна буде у нього входить.

Розглянемо вираз 10a+15a. Спробуємо винести у ньому загальний множник за дужки. Спочатку визначимо з чого складатиметься загальний множник, тобто дізнаємось його коефіцієнт і яка змінна буде в нього входити.

Коефіцієнтом загального множника буде найбільший загальний дільник коефіцієнтів буквеного виразу 10a+15a. 10 і 15 , а їх НОД це 5 . Значить число 5 буде коефіцієнтом загального множника, що виноситься за дужки.

Тепер визначимося яка змінна входитиме до загального множника. Для цього потрібно подивитися на вираз 10a+15aі знайти літерний співмножник, який входить у всі доданки. В даному випадку, це помножувач a. Цей помножувач входить у кожен доданок вирази 10a+15a. Значить змінна aвходитиме в літерну частину загального множника, що виноситься за дужки:

Тепер залишилося винести спільний множник 5aза дужки. Для цього розділимо кожне доданок вирази 10a+15aна 5a. Для наочності, коефіцієнти та числа відокремлюватимемо значком ×

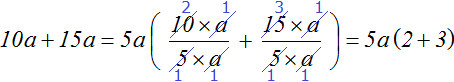
Перевіримо вираз на правильність. Для цього помножимо 5aна кожне доданок у дужках. Якщо ми все зробили правильно, то отримаємо вираз 10a+15a

Літерний множник не завжди можна винести за дужки. Іноді загальний множник складається тільки з числа тому, що нічого придатного для літерної частини у виразі не знаходиться.

Наприклад, винесемо загальний множник за дужки у виразі 2a-2b. Тут загальним множником, що виноситься за дужку буде лише число 2 , А серед літерних співмножників загальних множників у виразі немає. Тому в даному випадку буде винесено лише множник 2

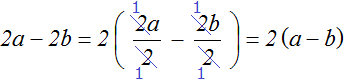
приклад 2.Винести загальний множник виразі 3x+9y+12

Коефіцієнтами цього виразу є числа 3, 9 і 12, їх НОД це 3 3 3

Приклад 3.Винести загальний множник за дужки у виразі 8x+6y+4z+10+2

Коефіцієнтами цього виразу є числа 8, 6, 4, 10 і 2, їх НОД це 2 . Значить коефіцієнтом загального множника, що виноситься за дужки, буде число 2 . А серед літерних співмножників (змінних) немає спільного множника. Тому остаточний загальний множник це 2

Приклад 4.Винести спільний множник 6ab+18ab+3abc

Коефіцієнтами цього виразу є числа 6, 18 та 3,їх НОД це 3 . Значить коефіцієнтом загального множника, що виноситься за дужки, буде число 3 . У літерну частину загального множника входитимуть змінні aі bоскільки у вираженні 6ab+18ab+3abcці дві змінні входять у кожний доданок. Тому остаточний загальний множник це 3ab

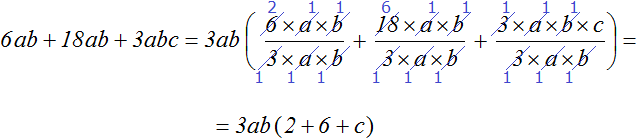
Напевно ви помітили, що при докладне рішеннявираз стає громіздким і навіть незрозумілим. У цьому прикладі це більш ніж помітно. Це з тим, що ми скорочуємо множники в чисельнику і в знаменнику.

Але допускається використовувати прямий розподіл чисельника на знаменник. В цьому випадку нічого скорочувати не потрібно:

Але найкраще робити це в умі і одразу записувати результати поділу. У цьому випадку вираз стає акуратнішим і коротшим:

Як і у випадку з числовим виразом у літерному виразі загальний множник може бути негативним.

Наприклад, винесемо загальний за дужки у виразі −3a −2a.

Для зручності замінимо віднімання додаванням

−3a −2a = −3a + (−2a )

Спільним множником у даному виразі є множник a. Але за дужки можна винести не лише a, але і −a. Його й винесемо за дужки:

Вийшов акуратний вираз −a (3+2).Не слід забувати, що множник −aнасправді виглядав як −1aі після скорочення в обох дробах змінних aУ знаменниках залишилися мінус одиниці. Тому в результаті і виходять позитивні відповіді у дужках

Приклад 6.Винести загальний множник за дужки у виразі −6x−6y

Замінимо віднімання додаванням

−6x−6y = −6x+(−6y)

Винесемо за дужки −6

Запишемо рішення коротше:

−6x−6y = −6(x+y)

Приклад 7.Винести загальний множник за дужки у виразі −2a−4b−6c

Замінимо віднімання додаванням

−2a-4b-6c = −2a + (−4b) + (−6c)

Винесемо за дужки −2

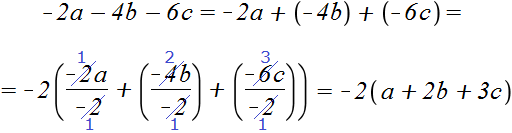
Вступай у нашу нову групуВконтакте та почні отримувати повідомлення про нові уроки

Як я вже зазначав, в інтегральному обчисленні немає зручної формули для інтегрування дробу. І тому спостерігається сумна тенденція: чим «навороченіший» дріб, тим важче знайти від нього інтеграл. У зв'язку з цим доводиться вдаватися до різних хитрощів, про які я зараз розповім.

Метод розкладання чисельника

Приклад 1

До речі, розглянутий інтеграл можна вирішити і методом заміни змінної, позначаючи , але запис рішення вийде значно довшим

Приклад 2

Знайти невизначений інтеграл. Виконати перевірку.

Це приклад самостійного рішення. Слід зазначити, що тут метод заміни змінної не пройде.

Увага, важливо! Приклади №№1,2 є типовими та зустрічаються часто. У тому числі подібні інтеграли нерідко виникають у ході вирішення інших інтегралів, зокрема при інтегруванні ірраціональних функцій (коренів).

Розглянутий прийом працює і у випадку, якщо старший ступінь чисельника, більший за старший ступінь знаменника.

Приклад 3

Знайти невизначений інтеграл. Виконати перевірку.

Починаємо підбирати чисельник.

Алгоритм підбору чисельника приблизно такий:

1) У чисельнику мені потрібно організувати, але там. Що робити? Укладаю в дужки і множу на : .

2) Тепер намагаюся розкрити ці дужки, що вийде? . Хмм ... вже краще, але ніякої двійки при спочатку в чисельнику немає. Що робити? Потрібно домножити на:

3) Знову розкриваю дужки: . А ось і перший успіх! Потрібний вийшов! Але проблема в тому, що з'явилося зайве доданок. Що робити? Щоб вираз не змінилося, я зобов'язаний додати до своєї конструкції те саме:
. Жити полегшало. А чи не можна ще раз у чисельнику організувати?

4) Можна. Пробуємо: . Розкриваємо дужки другого доданку:
. Вибачте, але в мене взагалі було на попередньому кроці, а не. Що робити? Потрібно домножити другий доданок на:

5) Знову для перевірки розкриваю дужки у другому доданку:
. Ось тепер нормально: отримано із остаточної конструкції пункту 3! Але знову є маленьке «але», з'явилося зайве доданок, отже, я повинен додати до свого висловлювання:

Якщо все виконано правильно, то при розкритті всіх дужок у нас має вийти вихідний чисельник підінтегральної функції. Перевіряємо:
Гуд.

Таким чином:

Готово. В останньому доданку я застосував метод підведення функції під диференціал.

Якщо знайти похідну від відповіді та привести вираз до спільного знаменника, то в нас вийде точно вихідна підінтегральна функція . Розглянутий спосіб розкладання на суму – є щось інше, як зворотне дію до приведення висловлювання до спільного знаменника.

Алгоритм підбору чисельника в подібних прикладах краще виконувати на чернетці. За деяких навичок виходитиме і подумки. Пригадую рекордний випадок, коли я виконував підбір для 11-го ступеня, і розкладання чисельника зайняло майже два рядки Верда.

Приклад 4

Знайти невизначений інтеграл. Виконати перевірку.

Це приклад самостійного рішення.

Метод підведення під знак диференціалу для найпростіших дробів

Переходимо до розгляду такого типу дробів.
, , , (коефіцієнти і не дорівнюють нулю).

Насправді пара випадків з арксинусом та арктангенсом вже прослизала на уроці Метод заміни змінної у невизначеному інтегралі. Вирішуються такі приклади способом підведення функції під знак диференціала та подальшим інтегруванням за допомогою таблиці. Ось ще типові приклади з довгим та високим логарифмом:

Приклад 5

Приклад 6

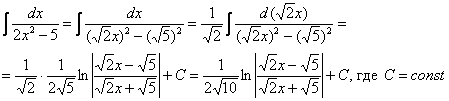
Тут доцільно взяти до рук таблицю інтегралів і простежити, за якими формулами якздійснюється перетворення. Зверніть увагу, як і навіщовиділяються квадрати у даних прикладах. Зокрема, у прикладі 6 спочатку необхідно уявити знаменник у вигляді , потім підвести під знак диференціалу А зробити це все потрібно для того, щоб скористатися стандартною табличною формулою.

Та що дивитися, спробуйте самостійно розв'язати приклади №№7,8, тим більше вони досить короткі:

Приклад 7

Приклад 8

Знайти невизначений інтеграл:

Якщо Вам вдасться виконати ще й перевірку цих прикладів, то великий респект – Ваші навички диференціювання на висоті.

Метод виділення повного квадрата

Інтеграли виду, (Коефіцієнти і не дорівнюють нулю) вирішуються методом виділення повного квадрата, який вже фігурував на уроці Геометричні перетворення графіків.

Насправді такі інтеграли зводяться до одного з чотирьох табличних інтегралів, які ми щойно розглянули. А досягається це за допомогою знайомих формул скороченого множення:

Формули застосовуються саме в такому напрямку, тобто, ідея методу полягає в тому, щоб у знаменнику штучно організувати вирази або , а потім перетворити їх відповідно на або .

Приклад 9

Знайти невизначений інтеграл

Це найпростіший приклад, у якому при доданку – одиничний коефіцієнт(а не якесь число або мінус).

Дивимося на знаменник, тут вся справа явно зведеться. Починаємо перетворення знаменника:

Очевидно, що потрібно додавати 4. І щоб вираз не змінилося – цю ж четвірку і віднімати:

Тепер можна застосувати формулу:

Після того, як перетворення закінчено ЗАВЖДИбажано виконати зворотний хід: все нормально, помилок немає.

Чистове оформлення прикладу, що розглядається, має виглядати приблизно так: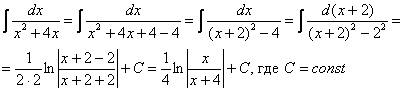

Готово. Підведенням «халявної» складної функції під знак диференціала: в принципі можна було знехтувати

Приклад 10

Знайти невизначений інтеграл:

Це приклад для самостійного вирішення, відповідь наприкінці уроку

Приклад 11

Знайти невизначений інтеграл:

Що робити, коли перед знаходиться мінус? І тут, необхідно винести мінус за дужки і розмістити доданки у необхідному нам порядке: . Константі(«двійку» у цьому випадку) не чіпаємо!

Тепер у дужках додаємо одиночку. Аналізуючи вираз, приходимо до висновку, що й за дужкою потрібно одиничку – додати:

Тут вийшла формула, застосовуємо:

ЗАВЖДИвиконуємо на чернетці перевірку:
, Що й потрібно перевірити.

Чистове оформлення прикладу виглядає приблизно так: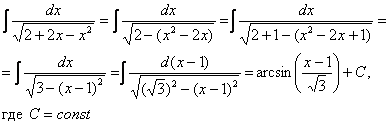

Ускладнюємо завдання

Приклад 12

Знайти невизначений інтеграл:

Тут при доданку вже не одиничний коефіцієнт, а «п'ятірка».

(1) Якщо знаходиться константа, то її відразу виносимо за дужки.

(2) І взагалі цю константу завжди краще винести за межі інтеграла, щоб вона не заважала під ногами.

(3) Очевидно, що все зведеться до формули. Треба розібратися в доданку, а саме, отримати «двійку»

(4) Ага, . Значить, до виразу додаємо, і цей же дріб віднімаємо.

(5) Тепер виділяємо повний квадрат. У загальному випадку також треба вирахувати, але тут у нас вимальовується формула довгого логарифму , і дію виконувати немає сенсу, чому – стане ясно трохи нижче.

(6) Власне, можна застосувати формулу , Тільки замість «ікс» у нас, що не скасовує справедливість табличного інтеграла. Строго кажучи, пропущено один крок - перед інтегруванням функцію слід підвести під знак диференціала: 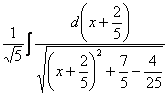Але, як я вже неодноразово зазначав, цим часто нехтують.

(7) У відповіді під корінням бажано розкрити всі дужки назад:

Важко? Це ще найскладніше в інтегральному обчисленні. Хоча, приклади, що розглядаються, не так складні, скільки вимагають хорошої техніки обчислень.

Приклад 13

Знайти невизначений інтеграл:

Це приклад самостійного рішення. Відповідь наприкінці уроку.

Існують інтеграли з корінням у знаменнику, які за допомогою заміни зводяться до інтегралів розглянутого типу, про них можна прочитати у статті Складні інтегралиале вона розрахована на дуже підготовлених студентів.

Підведення чисельника під знак диференціалу

Це заключна частина уроку, проте інтеграли такого типу зустрічаються досить часто! Якщо накопичилася втома, може, воно краще завтра почитати? ;)

Інтеграли, які ми будемо розглядати, схожі на інтеграли попереднього параграфа, вони мають вигляд: або (Коефіцієнти , і не дорівнюють нулю).

Тобто, у чисельнику ми з'явилася лінійна функція. Як вирішувати такі інтеграли?

Приклад 14

Знайти невизначений інтеграл:

Перетворення виразів

Часто ми чуємо цю неприємну фразу: спростіть вираз. Зазвичай при цьому перед нами якесь страшнисько типу цього:

"Та куди вже простіше" - говоримо ми, але така відповідь зазвичай не прокочує.

Зараз я навчу тебе не боятися жодних таких завдань. Більше того, наприкінці заняття ти сам спростиш цей приклад до всього лише! звичайного числа(так-так, до біса ці літери).

Але перш ніж приступити до цього заняття, тобі необхідно вміти поводитися з дробами та розкладати багаточлени на множники. Тому спершу, якщо ти цього не зробив раніше, обов'язково освою теми «» та «».

Прочитав? Якщо так, то тепер готовий.

Базові операції спрощення

Зараз розберемо основні прийоми, що використовуються при спрощенні виразів.

Найпростіший з них – це

1. Приведення подібних

Що таке? Ти проходив це у 7 класі, як тільки вперше в математиці з'явилися літери замість чисел. Подібні – це доданки (одночлени) з однаковою літерною частиною. Наприклад, у сумі подібні доданки – це і.

Згадав?

Привести подібні - значить скласти кілька подібних доданків один з одним і отримати один доданок.

А як нам скласти один з одним літери? - Запитаєш ти.

Це дуже легко зрозуміти, якщо уявити, що літери – це якісь предмети. Наприклад, літера – це стілець. Тоді чому дорівнює вираз? Два стільці плюс три стільці, скільки буде? Правильно, стільців: .

А тепер спробуй такий вираз: .

Щоб не заплутатися, нехай різні літери позначають різні предмети. Наприклад, - це (як завжди) стілець, а - це стіл. Тоді:

стільця столу стілець стільців стільців стільців столів

Числа, на які множаться літери в таких доданках, називаються коефіцієнтами. Наприклад, в одночлен коефіцієнт дорівнює. А він дорівнює.

Отже, правило приведення таких:

Приклади:

Наведіть такі:

Відповіді:

2. (і подібні, тому що, отже у цих доданків однакова літерна частина).

2. Розкладання на множники

Це зазвичай найважливіша частина у спрощенні виразів. Після того, як ти навів подібні, найчастіше отриманий вираз потрібно розкласти на множники, тобто подати у вигляді твору. Особливо це важливо у дробах: адже щоб можна було скоротити дріб, чисельник та знаменник мають бути представлені у вигляді твору.

Детально способи розкладання виразів на множники ти проходив у темі « », тому тут тобі залишається лише згадати вивчене. Для цього виріши кілька прикладів(Потрібно розкласти на множники):

Рішення:

3. Скорочення дробу.

Ну що може бути приємніше, ніж закреслити частину чисельника та знаменника, та викинути їх зі свого життя?

У цьому вся краса скорочення.

Все просто:

Якщо чисельник і знаменник містять однакові множники, їх можна скоротити, тобто забрати з дробу.

Це правило випливає з основної властивості дробу:

Тобто суть операції скорочення в тому, що чисельник і знаменник дробу ділимо одне й те саме число (чи одне й те саме вираз).

Щоб скоротити дріб, потрібно:

1) чисельник та знаменник розкласти на множники

2) якщо в чисельнику та знаменнику є загальні множники, їх можна викреслити.

Принцип, я гадаю, зрозумілий?

Хочу звернути увагу на одну типову помилкупри скороченні. Хоч ця тема і проста, але дуже багато хто робить все неправильно, не розуміючи, що скоротити- це означає поділитичисельник і знаменник одне й те саме число.

Жодних скорочень, якщо в чисельнику чи знаменнику сума.

Наприклад: треба спростити.

Деякі роблять так: що абсолютно неправильно.

Ще приклад: скоротити.

«Найрозумніші» зроблять так: .

Скажи мені, що тут не так? Здавалося б: це множник, значить можна скорочувати.

Але ні: – це множник лише одного доданку в чисельнику, але сам чисельник загалом на множники не розкладено.

Ось інший приклад: .

– це вираз розкладено на множники, отже, можна скоротити, тобто поділити чисельник і знаменник на, та був і:

Можна і відразу поділити на:

Щоб не допускати подібних помилок, запам'ятай легкий спосіб, як визначити, чи розкладено вираз на множники:

Арифметична дія, яка виконується останнім при підрахунку значення виразу, є «головною». Тобто, якщо ти підставиш замість літер якісь (будь-які) числа, і спробуєш обчислити значення виразу, то якщо останньою дією буде множення – значить, у нас твір (вираз розкладено на множники). Якщо останнім дією буде додавання чи віднімання, це означає, що вираз не розкладено на множники (отже, скорочувати не можна).

Для закріплення виріши самостійно кілька прикладів:

Відповіді:

1. Сподіваюся, ти не кинувся зразу ж скорочувати і? Ще не вистачало «скоротити» одиниці типу:

Першим дією має бути розкладання на множники:

4. Додавання та віднімання дробів. Приведення дробів до спільного знаменника.

Складання та віднімання звичайних дробів- Операція добре знайома: шукаємо спільний знаменник, домножуємо кожен дріб на недостатній множник і складаємо/віднімаємо чисельники. Давай згадаємо:

Відповіді:

1. Знаменники і – взаємно прості, тобто вони не мають спільних множників. Отже, НОК цих чисел дорівнює їхньому твору. Це і буде спільний знаменник:

2. Тут спільний знаменник дорівнює:

3. Тут насамперед змішані дробиперетворюємо на неправильні, а далі – за звичною схемою:

Зовсім інша справа, якщо дроби містять букви, наприклад:

Почнемо з простого:

a) Знаменники не містять літер

Тут все те ж, що і зі звичайними числовими дробами: знаходимо спільний знаменник, домножуємо кожен дріб на множник, що бракує, і складаємо/віднімаємо чисельники:

тепер у чисельнику можна наводити подібні, якщо є, і розкладати на множники:

Спробуй сам:

b) Знаменники містять літери

Пригадаймо принцип знаходження спільного знаменника без літер:

· Насамперед ми визначаємо загальні множники;

· Потім виписуємо всі загальні множники по одному разу;

· І домножуємо їх на всі інші множники, не спільні.

Щоб визначити спільні множники знаменників, спочатку розкладемо їх на прості множники:

Підкреслимо спільні множники:

Тепер випишемо спільні множники по одному разу і допишемо до них усі загальні (не підкреслені) множники:

- Це і є спільний знаменник.

Повернемося до букв. Знаменники наводяться за такою ж схемою:

· Розкладаємо знаменники на множники;

· Визначаємо загальні (однакові) множники;

· Виписуємо всі загальні множники по одному разу;

· Домножуємо їх на всі інші множники, не загальні.

Отже, по порядку:

1) розкладаємо знаменники на множники:

2) визначаємо загальні (однакові) множники:

3) виписуємо всі загальні множники по одному разу і примножуємо їх на всі інші (непідкреслені) множники:

Виходить, спільний знаменник тут. Перший дріб потрібно домножити на, другий – на:

До речі, є одна хитрість:

Наприклад: .

Бачимо в знаменниках одні і ті ж множники, тільки всі різними показниками. До спільного знаменника підуть:

у ступені

у ступені

у ступені

у ступені.

Ускладнимо завдання:

Як зробити у дробів однаковий знаменник?

Давай згадаємо основну властивість дробу:

Ніде не сказано, що з чисельника та знаменника дробу можна віднімати (або додавати) одне й те саме число. Тому що це не так!

Переконайся сам: візьми будь-який дріб, наприклад, і додай до чисельника і знаменника якесь число, наприклад, . Що повчилося?

Отже, чергове непорушне правило:

Коли наводиш дроби до спільного знаменника, користуйся лише операцією множення!

Але на що ж треба примножити, щоби отримати?

Ось на і домнож. А примножуй на:

Вирази, які неможливо розкласти на множники називатимемо «елементарними множниками». Наприклад, це елементарний множник. – теж. А ось – ні: він розкладається на множники.

Що скажеш щодо виразу? Воно елементарне?

Ні, оскільки його можна розкласти на множники:

(про розкладання на множники ти вже читав у темі «Розділ»).

Так ось, елементарні множники, на які ти розкладаєш вираз із літерами – це аналог простих множників, на які ти розкладаєш числа. І робитимемо з ними таким же чином.

Бачимо, що в обох знаменниках є множник. Він піде у спільний знаменник у мірі (пам'ятаєш, чому?).

Множник - елементарний, і він у них не загальний, значить перший дріб на нього доведеться просто примножити:

Ще приклад:

Рішення:

Перш ніж у паніці перемножувати ці знаменники, треба подумати, як їх розкласти на множники? Обидва вони представляють формули скороченого множення:

Чудово! Тоді:

Ще приклад:

Рішення:

Як завжди, розкладемо знаменники на множники. У першому знаменнику просто виносимо за дужки; у другому – різниця квадратів:

Здавалося б, спільних множників немає. Але якщо придивитися, то й так схожі… І справді:

Так і напишемо:

Тобто вийшло так: усередині дужки ми поміняли подекуди, і при цьому знак перед дробом помінявся на протилежний. Візьми на замітку, так робити доведеться часто.

Тепер приводимо до спільного знаменника:

Засвоїв? Зараз перевіримо.

Завдання для самостійного вирішення:

Відповіді:

Тут треба згадати ще одну – різницю кубів:

Зверніть увагу, що у знаменнику другого дробу не формула «квадрат суми»! Квадрат суми виглядав так: .

А – це так званий неповний квадрат суми: другий доданок у ньому – це твір першого та останнього, а не подвоєний їхній твір. Неповний квадрат суми – це один із множників у розкладанні різниці кубів:

Що робити, якщо дробів аж три штуки?

Та те саме! Насамперед зробимо так, щоб максимальна кількість множників у знаменниках була однаковою:

Зверніть увагу: якщо поміняти знаки всередині однієї дужки, знак перед дробом змінюється на протилежний. Коли міняємо знаки у другій дужці, знак перед дробом знову змінюється на протилежний. В результаті він (знак перед дробом) не змінився.

До загального знаменника виписуємо повністю перший знаменник, а потім дописуємо до нього всі множники, які ще не написані, з другого, а потім із третього (і так далі, якщо дробів більше). Тобто виходить так:

Хм... З дробами зрозуміло що робити. Але як бути з двійкою?

Все просто: адже ти вмієш складати дроби? Отже, треба зробити так, щоб двійка стала дробом! Згадуємо: дріб – це операція розподілу (числитель поділяється на знаменник, якщо ти раптом забув). І немає нічого простішого, ніж розділити число на. При цьому саме число не зміниться, але перетвориться на дріб:

Те що потрібно!

5. Множення та розподіл дробів.

Що ж, найскладніше тепер позаду. А попереду у нас найпростіше, але при цьому найважливіше:

Порядок дій

Який порядок дій при підрахунку числового виразу? Згадай, порахувавши значення такого виразу:

Порахував?

Повинно вийти.

Отже, нагадую.

Насамперед обчислюється ступінь.

Другим – множення та розподіл. Якщо множень і поділок одночасно кілька, робити їх можна у будь-якому порядку.

І наостанок виконуємо складання та віднімання. Знову ж таки, в будь-якому порядку.

Але: вираз у дужках обчислюється позачергово!

Якщо кілька дужок множаться або діляться один на одного, обчислюємо спочатку вираз у кожній із дужок, а потім множимо або поділи їх.

А якщо всередині дужок є ще одні дужки? Ну давай подумаємо: усередині дужок написаний якийсь вираз. А при обчисленні виразу насамперед треба робити що? Правильно, обчислювати дужки. Ну ось і розібралися: спочатку обчислюємо внутрішні дужки, потім решту.

Отже, порядок дій для вираження вище такий (червоним виділено поточне дію, тобто дію, яке виконую зараз):

Добре, це просто.

Але ж це не те саме, що вираз з літерами?

Ні, це те саме! Тільки замість арифметичних дійтреба робити алгебраїчні, тобто дії, описані в попередньому розділі: приведення подібних, додавання дробів, скорочення дробів і так далі. Єдиною відмінністю буде дія розкладання багаточленів на множники (його часто застосовуємо під час роботи з дробами). Найчастіше для розкладання на множники потрібно застосовувати формули скороченого множення або просто виносити загальний множник за дужки.

Зазвичай наша мета – уявити вираз у вигляді твору чи приватного.

Наприклад:

Спростимо вираз.

1) Першим спрощуємо вираз у дужках. Там у нас різниця дробів, а наша мета – уявити її як твір чи приватний. Отже, наводимо дроби до спільного знаменника і складаємо:

Більше цього виразу спростити неможливо, всі множники тут – елементарні (ти ще пам'ятаєш, що це означає?).

2) Отримуємо:

Розмноження дробів: що може бути простішим.

3) Тепер можна і скоротити:

Ну от і все. Нічого складного, правда?

Ще приклад:

Спрости вираз.

Спочатку спробуй вирішити сам, і вже потім подивися рішення.

Насамперед визначимо порядок дій. Спочатку виконаємо складання дробів у дужках, вийде замість двох дробів один. Потім виконаємо поділ дробів. Ну і результат складемо з останнім дробом. Схематично пронумерую дії:

Тепер покажу звістку процес, підфарбовуючи поточну дію червоним:

Насамкінець дам тобі дві корисні поради:

1. Якщо є такі, їх треба негайно навести. У який би момент у нас не утворилися подібні, їх бажано наводити одразу.

2. Те саме стосується скорочення дробів: як тільки з'являється можливість скоротити, їй треба скористатися. Виняток становлять дроби, які ти складаєш або віднімаєш: якщо у них зараз однакові знаменникито скорочення треба залишити на потім.

Ось тобі завдання для самостійного вирішення:

І обіцяна на самому початку:

Рішення (короткі):

Якщо ти впорався хоча б із першими трьома прикладами, то тему ти, вважай, опанував.

Тепер уперед до навчання!

Чому цій темі присвячено окремий відеоурок? Справа в тому, що зустрічаючи дроби з негативними числамиБагато учнів часто припускаються помилок, які, втім, легко уникнути, якщо розглянути цей метод.

Даний метод, який ми зараз розглянемо, полягає в тому, щоб привести дріб до зручного для нас вигляду, з яким ми вже нічого не наплутаємо.

Для початку давайте подивимося на елементарні приклади:

1) Скільки буде "дванадцять ділити на мінус чотири"?... Звичайно ж, "мінус три".

2) А скільки буде "мінус дванадцять розділити на чотири"?Теж "мінус три"!

3) А якщо так: "мінус... дванадцять ділити на чотири"? І тут також отримаємо "мінус три".

А тепер, якщо ми згадаємо, що дріб - це поділ, і межу дробу можна написати замість знака поділу, то отримаємо таке:...

Ну а оскільки ці дроби рівні одному й тому ж числу, то вони рівні між собою.

А з цього запису ми бачимо, що зовсім неважливо де стоїть мінус: перед межею дробу, в чисельнику чи знаменнику! Результат виходить однаковим.

Давайте застосуємо це знання до вирішення конкретного прикладу.

Мінус одна четверта плюс п'ять третіх мінус три п'ятих мінус сім других.

Першим кроком перетворимо цей запис на додавання чотирьох доданків. Тобто з мінусів зробимо плюси, адже ми знаємо, що "мінус а" те саме, щота "плюс... мінус а".

Значить "мінус одна четверта" - це плюс мінус одна четверта - ну тут плюс можна не писати, так як перед плюсом нічого немає. Потім, "мінус три п'яті" - це "плюс... мінус три п'яті". І "мінус сім других" - це "плюс... мінус сім других".

Ну а тепер ці мінуси перед знаками дробів можна забрати в чисельники... і тоді дужки вже не будуть потрібні... ми отримаємо складання чотирьох дробів з різними знаменниками.

Вирішити цей приклад вже набагато простіше, можна не боятися заплутатися у мінусах.

Наводимо дроби до спільного знаменника. Тут він дорівнюватиме... шістдесят.

Чисельник і знаменник першого дробу примножуємо на п'ятнадцять, другого - на двадцять, третього - на дванадцять і четвертого - на тридцять...

Пишемо спільний знаменник – шістдесят. А в загальний чисельник записуємо по порядку ті числа, які у нас вийдуть тут: мінус п'ятнадцять, плюс сто, мінус тридцять шість, мінус двісті десять. Якби ми не виконали перший крок і ось тут у нас залишилися стояти мінуси, то ми легко могли б заплутатися зі знаками. А так, коли тут лише плюси, ми просто записуємо в чисельник одержані числа з такими знаками, з якими ми їх отримали. Якщо "п'ять помножити на двадцять" було "сто", то й пишемо "плюс сто". А якщо "мінус три" помножити на дванадцять – це "мінус тридцять шість", то так і пишемо мінус тридцять шість.

У цьому є секрет даного методу. І які б складні були приклади, застосовуючи даний метод, ви ніколи не заплутаєтеся в знаках.

Ну, а тут нам залишилося порахувати чисельник... Це буде мінус сто шістдесят один. Мінус можна написати перед знаком дробу. До речі, у відповіді завжди краще саме перед знаком дробу писати мінус. Так прийнято... Ну можна ще виділити цілу частину... Це буде... мінус дві сорок одна шістдесята.

Отже, повторимо наш метод:

"У прикладах зі складанням/відніманням дробів першим кроком перетворюємо віднімання на додавання (для цього прибираємо знак "мінус" у дужки). Далі переносимо знак "мінус" перед дробами в чисельники і просто виконуємо складання дробів".

Важливий момент - ви повинні не тільки запам'ятати це правило, але і чітко розуміти його, щоб успішно застосовувати при вирішенні прикладів.

У наступному уроці ми розглянемо дуже важливі зауваження, про які вам потрібно пам'ятати, вирішуючи приклади з дробами.