Спрощення алгебраїчних дробів. Перетворення виразів. Докладна теорія
На даному уроці буде розглянуто основну властивість дробу алгебри. Уміння правильно і без помилок застосовувати цю властивість є одним з найважливіших базових умінь у всьому курсі шкільної математики і буде зустрічатися не тільки протягом вивчення даної теми, а й практично у всіх розділах математики, що вивчаються в подальшому. Раніше вже було вивчено скорочення звичайних дробів, але в цьому уроці буде розглянуто скорочення раціональних дробів. Незважаючи на досить велику зовнішню відмінність, що існує між раціональними та звичайними дробами, у них дуже багато спільного, а саме – і звичайним, і раціональним дробамвластиві однакова основна властивість і загальні правилавиконання арифметичних дій. У рамках уроку ми зіткнемося з поняттями: скорочення дробу, множення та розподіл чисельника та знаменника на один і той самий вираз – і розглянемо приклади.
Тема:Алгебраїчні дроби.Арифметичні операції над алгебраїчними дробами
Урок:
1. Основна властивість звичайного дробу
Згадаймо основне властивість звичайного дробу : значення дробу не зміниться, якщо його чисельник і знаменник одночасно помножити або розділити на те саме відмінне від нуля число. Нагадаємо, що розподіл чисельника і знаменника дробу на те саме відмінне від нуля число називається скороченням.
Наприклад: , у своїй значення дробів не змінюється. Однак часто при застосуванні даної властивості багато хто припускається стандартних помилок:
1. 
- у наведеному прикладі припущена помилка поділу тільки одного доданку з чисельника на 2, а не всього чисельника. Правильна послідовність дій виглядає так: 
або .
2. 
- тут ми бачимо схожу помилку, однак, крім цього, ще в результаті розподілу отримано 0, а не 1, що є ще більш частою і грубою помилкою.
Тепер потрібно перейти до розгляду алгебраїчного дробу. Згадаймо це поняття з попереднього уроку.
Визначення. Раціональний (алгебраїчний) дріб - дробовий виразвиду, де - багаточлени. - чисельник знаменник.
Алгебраїчні дроби є, у певному сенсі, узагальненням звичайних дробів, і з них можна проводити самі операції, як і над звичайними дробами.
2. Основна властивість алгебраїчного дробу
Основна властивість алгебраїчного дробу- і чисельник, і знаменник дробу можна множити і ділити на той самий багаточлен (одночлен) або число, відмінне від нуля. Це буде тотожне перетворення алгебраїчного дробу. Згадаймо, що, як і раніше, розподіл чисельника і знаменника дробу на те саме відмінне від нуля вираз називається скороченням.
Основна властивість алгебраїчного дробудозволяє скорочувати дроби та приводити їх до найменшого спільному знаменнику.
3. Приклади скорочення звичайних дробів
Для скорочення звичайних дробів ми вдавалися до основний теоремі арифметики, Розкладали і чисельник, і знаменник на прості множники
Визначення. Просте число- Натуральне число, яке ділиться тільки на одиницю і саме себе. Всі решта натуральні числаназиваються складовими. 1 не є ні простим, ні складовим числом.
Приклад 1. а), де множники, на які розкладено чисельники та знаменники зазначених дробів, є простими числами.
4. Приклади скорочення алгебраїчних дробів
Отже, для скорочення дробівнеобхідно попередньо розкласти на множники чисельник і знаменник дробу, та був розділити їх у загальні множники. Т. е. слід володіти методами розкладання многочленів на множники.
Приклад 2. Скоротити дріб а), б), в).
Рішення. а) 
. Слід зазначити, що у чисельнику перебуває повний квадрат, а знаменнику - різниця квадратів. Після скорочення необхідно вказати, що , щоб уникнути розподілу на нуль.
б) 
. У знаменнику виноситься загальний числовий множник, що корисно робити практично у будь-якому разі, коли це можливо. Аналогічно з попереднім прикладом вказуємо, що .
в) 
. У знаменнику виносимо за дужки мінус (або формально). Не забуваймо, що при скороченні .
Відповідь. ;;; .
Тепер наведемо приклад на приведення до спільного знаменника, робиться це аналогічно до звичайних дробів.
5. Приведення звичайних дробів до спільного знаменника
Приклад 3. Привести до спільного знаменника дробу та .
Рішення. Для знаходження найменшого спільного знаменника потрібно знайти найменше загальне кратне (НОК) двох знаменників, тобто НОК (3; 5). Іншими словами, знайти найменше число, яке ділиться на 3 та 5 одночасно. Очевидно, що це число 15, записати це можна таким чином: НОК (3; 5) = 15 - це буде спільний знаменник зазначених дробів.
Щоб перетворити знаменник 3 в 15, його необхідно помножити на 5, а для перетворення 5 в 15, його необхідно помножити на 3. За основною властивістю дробу алгебри слід помножити на ті ж числа і відповідні чисельники зазначених дробів.
Приклад 4. Привести до спільного знаменника дробу та .
Рішення. Проведемо аналогічні до попереднього прикладу дії. Найменше загальне кратне знаменників НОК (12; 18) = 36. Приведемо до цього знаменника обидва дроби:
6. Скорочення складних звичайних дробів
Тепер розглянемо приклади, що демонструють застосування техніки скорочення дробів їх спрощення у складніших випадках.
Приклад 5. Обчислити значення дробу: а), б), в).
а) . При скороченні користуємося правилом поділу ступенів.
7. Скорочення складних алгебраїчних дробів
Після того, як ми повторили використання основної якості звичайного дробу, можна перейти до розгляду алгебраїчних дробів.
Приклад 6. Спростити дріб та обчислити при заданих значеннях змінних: а) ; 
, б); 
Рішення. При підході до рішення можливий наступний варіант - відразу ж підставити значення змінних і почати розрахунок дробу, але в такому випадку рішення сильно ускладнюється, і необхідне його рішення час збільшується, не кажучи вже про небезпеку помилитися в складних обчисленнях. Тому зручно спочатку спростити вираз у літерному вигляді, а потім підставити значення змінних.
а) . При скороченні на множник необхідно перевірити, чи він в нуль у зазначених значеннях змінних. При підстановці отримуємо , що дозволяє скорочення на даний множник.
б). У знаменнику виносимо мінус, як ми це вже робили в прикладі 2. При скороченні знову перевіряємо, чи не ділимо ми на нуль: .
8. Приведення алгебраїчних дробів до спільного знаменника
Приклад 7. Привести до спільного знаменника дробу а) та , б) та , в) та .
Рішення. а) В даному випадку підійдемо до рішення наступним чином: не користуватимемося поняттям НОК, як у другому прикладі, а просто помножимо знаменник першого дробу на знаменник другого, і навпаки - це дозволить привести дроби до однакового знаменника. Звичайно ж, не забуваймо при цьому множити і чисельники дробів на такі ж вирази.
У цій статті ми розглянемо основні дії з алгебраїчними дробами:
- скорочення дробів
- множення дробів
- розподіл дробів
Почнемо з скорочення алгебраїчних дробів.
Здавалося б, алгоритмочевидний.
Щоб скоротити алгебраїчні дроби, потрібно
1. Розкласти чисельник та знаменник дробу на множники.
2. Скоротити однакові множники.
Проте, школярі часто роблять помилку, "зменшуючи" не множники, а доданки. Наприклад, є любителі, які в дробі "зменшують" і отримують в результаті, що, зрозуміло, неправильно.
Розглянемо приклади:
1.
Скоротити дріб: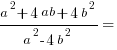 
1. Розкладемо на множники чисельник за формулою квадрата суми, а знаменник за формулою різниці квадратів
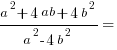
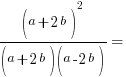
2. Розділимо чисельник та знаменник на
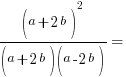
2.
Скоротити дріб: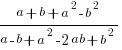 
1. Розкладемо на множники чисельник. Оскільки чисельник містить чотири доданки, застосуємо угруповання.
2. Розкладемо на множники знаменник. Так само застосуємо угруповання.
3. Запишемо дріб, який у нас вийшов і скоротимо однакові множники:
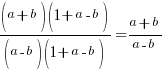
Розмноження алгебраїчних дробів.
При множенні дробів алгебри ми чисельник множимо на чисельник, а знаменник множимо на знаменник.
Важливо!Не потрібно поспішати виконувати множення у чисельнику та знаменнику дробу. Після того, як ми записали в чисельнику добуток чисельників дробів, а в знаменнику - добуток знаменників, потрібно розкласти на множники кожен множник і скоротити дріб.
Розглянемо приклади:
3. Спростіть вираз:
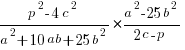
1. Запишемо добуток дробів: у чисельнику добуток чисельників, а у знаменнику добуток знаменників:
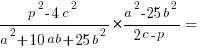
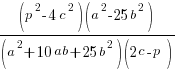
2. Розкладемо кожну дужку на множники:
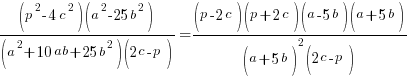
Тепер нам потрібно скоротити однакові множники. Зауважимо, що вирази і відрізняються лише знаком: 
і в результаті розподілу першого виразу на друге отримаємо -1.
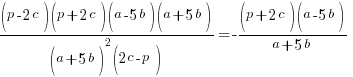
Отже,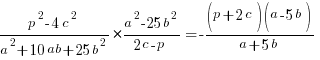 
Розподіл алгебраїчних дробів ми виконуємо за таким правилом:
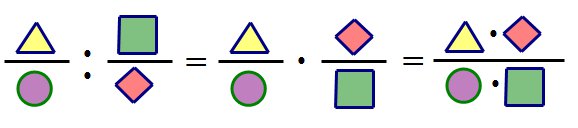Тобто щоб розділити на дріб, потрібно помножити на "перевернутий".
Ми, що розподіл дробів зводиться до множення, а множення, зрештою, зводиться до скорочення дробів.
Розглянемо приклад:
4. Спростіть вираз:
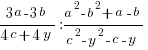
Засновано на їхній основній властивості: якщо чисельник і знаменник дробу розділити на той самий ненульовий багаточлен, то вийде рівний їй дріб.
Скорочувати можна лише множники!
Члени багаточленів скорочувати не можна!
Щоб скоротити алгебраїчну дріб, багаточлени, що стоять у чисельнику та знаменнику, потрібно попередньо розкласти на множники.
Розглянемо приклади скорочення дробів.
У чисельнику та знаменнику дробу стоять одночлени. Вони є твір(чисел, змінних та їх ступенів), множникискорочувати можемо.
Числа скорочуємо з їхньої найбільший спільний дільник, тобто найбільше, куди ділиться кожне з цих чисел. Для 24 та 36 це – 12. Після скорочення від 24 залишається 2, від 36 – 3.
Ступені скорочуємо на ступінь із найменшим показником. Скоротити дріб - значить, розділити чисельник і знаменник на той самий дільник, а показники віднімаємо.
a² та a⁷ скорочуємо на a². При цьому в чисельнику від a² залишається одиниця (1 пишемо тільки в тому випадку, коли окрім неї після скорочення інших множників не залишилося. Від 24 залишилася 2, тому 1, що залишилася від a², не пишемо). Від a⁷ після скорочення залишається a⁵.
b та b скорочуємо на b, отримані в результаті одиниці не пишемо.
c³º та с⁵ скорочуємо на с⁵. Від c³º залишається c²⁵, від с⁵ — одиниця (її не пишемо). Таким чином,
Чисельник і знаменник даного дробу алгебри - багаточлени. Скорочувати члени багаточленів не можна! (Не можна скоротити, наприклад, 8x² і 2x!). Щоб скоротити цей дріб, треба . У чисельнику є загальний множник 4x. Виносимо його за дужки:
І в чисельнику, і в знаменнику є однаковий множник (2x-3). Скорочуємо дріб на цей множник. У чисельнику отримали 4x, у знаменнику - 1. По 1 властивості алгебраїчних дробів, дріб дорівнює 4x.
Скорочувати можна лише множники (скоротити цей дрібна 25x² не можна!). Тому багаточлени, що стоять у чисельнику та знаменнику дробу, потрібно розкласти на множники.
У чисельнику – повний квадрат суми, у знаменнику – різниця квадратів. Після розкладання за формулами скороченого множення отримуємо:
Скорочуємо дріб на (5x+1) (для цього в чисельнику закреслимо двійку у показник ступеня, від (5x+1)² при цьому залишиться (5x+1)):
У чисельнику є загальний множник 2, винесемо його за дужки. У знаменнику - формула різниці кубів:
В результаті розкладання в чисельнику та знаменнику отримали однаковий множник (9+3a+a²). Скорочуємо дріб на нього:
Багаточлен у чисельнику складається з 4 доданків. перше доданок з другим, третє - з четвертим і виносимо з перших дужок загальний множник x². Знаменник розкладаємо за формулою суми кубів:
У чисельнику винесемо за дужки загальний множник (x+2):
Скорочуємо дріб на (x+2):
Перетворення виразів
Часто ми чуємо цю неприємну фразу: спростіть вираз. Зазвичай при цьому перед нами якесь страшнисько типу цього:
"Та куди вже простіше" - говоримо ми, але така відповідь зазвичай не прокочує.
Зараз я навчу тебе не боятися жодних таких завдань. Більше того, наприкінці заняття ти сам спростиш цей приклад до всього лише! звичайного числа(так-так, до біса ці літери).
Але перш ніж приступити до цього заняття, тобі необхідно вміти поводитися з дробами та розкладати багаточлени на множники. Тому спершу, якщо ти цього не зробив раніше, обов'язково освою теми «» та «».
Прочитав? Якщо так, то тепер готовий.
Базові операції спрощення
Зараз розберемо основні прийоми, що використовуються при спрощенні виразів.
Найпростіший з них – це
1. Приведення подібних
Що таке? Ти проходив це у 7 класі, як тільки вперше в математиці з'явилися літери замість чисел. Подібні – це доданки (одночлени) з однаковою літерною частиною. Наприклад, у сумі подібні доданки – це і.
Згадав?
Привести подібні - значить скласти кілька подібних доданків один з одним і отримати один доданок.
А як нам скласти один з одним літери? - Запитаєш ти.
Це дуже легко зрозуміти, якщо уявити, що літери – це якісь предмети. Наприклад, літера – це стілець. Тоді чому дорівнює вираз? Два стільці плюс три стільці, скільки буде? Правильно, стільців: .
А тепер спробуй такий вираз: .
Щоб не заплутатися, нехай різні літери позначають різні предмети. Наприклад, - це (як завжди) стілець, а - це стіл. Тоді:
стільця столу стілець стільців стільців стільців столів
Числа, на які множаться літери в таких доданках, називаються коефіцієнтами. Наприклад, в одночлен коефіцієнт дорівнює. А він дорівнює.
Отже, правило приведення таких:
Приклади:
Наведіть такі:
Відповіді:
2. (і подібні, тому що, отже у цих доданків однакова літерна частина).
2. Розкладання на множники
Це зазвичай найважливіша частина у спрощенні виразів. Після того, як ти навів подібні, найчастіше отриманий вираз потрібно розкласти на множники, тобто подати у вигляді твору. Особливо це важливо в дробах: адже щоб можна було скоротити дріб, чисельник та знаменник мають бути представлені у вигляді твору.
Детально способи розкладання виразів на множники ти проходив у темі « », тому тут тобі залишається лише згадати вивчене. Для цього виріши кілька прикладів(Потрібно розкласти на множники):
Рішення:
3. Скорочення дробу.
Ну що може бути приємніше, ніж закреслити частину чисельника та знаменника, та викинути їх зі свого життя?
У цьому вся краса скорочення.
Все просто:
Якщо чисельник і знаменник містять однакові множники, їх можна скоротити, тобто забрати з дробу.
Це правило випливає з основної властивості дробу:
Тобто суть операції скорочення в тому, що чисельник і знаменник дробу ділимо одне й те саме число (чи одне й те саме вираз).
Щоб скоротити дріб, потрібно:
1) чисельник та знаменник розкласти на множники
2) якщо в чисельнику та знаменнику є загальні множники, їх можна викреслити.
Принцип, я гадаю, зрозумілий?
Хочу звернути увагу на одну типову помилкупри скороченні. Хоч ця тема і проста, але дуже багато хто робить все неправильно, не розуміючи, що скоротити- це означає поділитичисельник і знаменник одне й те саме число.
Жодних скорочень, якщо в чисельнику чи знаменнику сума.
Наприклад: треба спростити.
Деякі роблять так: що абсолютно неправильно.
Ще приклад: скоротити.
«Найрозумніші» зроблять так: .
Скажи мені, що тут не так? Здавалося б: це множник, значить можна скорочувати.
Але ні: – це множник лише одного доданку в чисельнику, але сам чисельник загалом на множники не розкладено.
Ось інший приклад: .
– це вираз розкладено на множники, отже, можна скоротити, тобто поділити чисельник і знаменник на, та був і:
Можна і відразу поділити на:
Щоб не допускати подібних помилок, запам'ятай легкий спосіб, як визначити, чи розкладено вираз на множники:
Арифметична дія, яка виконується останнім при підрахунку значення виразу, є «головною». Тобто, якщо ти підставиш замість літер якісь (будь-які) числа, і спробуєш обчислити значення виразу, то якщо останньою дією буде множення – значить, у нас твір (вираз розкладено на множники). Якщо останнім дією буде додавання чи віднімання, це означає, що вираз не розкладено на множники (отже, скорочувати не можна).
Для закріплення виріши самостійно кілька прикладів:
Відповіді:
1. Сподіваюся, ти не кинувся зразу ж скорочувати і? Ще не вистачало «скоротити» одиниці типу:
Першим дією має бути розкладання на множники:
4. Додавання та віднімання дробів. Приведення дробів до спільного знаменника.
Складання та віднімання звичайних дробів- Операція добре знайома: шукаємо спільний знаменник, домножуємо кожен дріб на відсутній множник і складаємо/віднімаємо чисельники. Давай згадаємо:
Відповіді:
1. Знаменники і – взаємно прості, тобто вони не мають спільних множників. Отже, НОК цих чисел дорівнює їхньому твору. Це і буде спільний знаменник:
2. Тут спільний знаменник дорівнює:
3. Тут насамперед змішані дробиперетворюємо на неправильні, а далі – за звичною схемою:
Зовсім інша справа, якщо дроби містять букви, наприклад:
Почнемо з простого:
a) Знаменники не містять літер
Тут все те саме, що і зі звичайними числовими дробами: знаходимо спільний знаменник, домножуємо кожен дріб на відсутній множник і складаємо/віднімаємо чисельники:
тепер у чисельнику можна наводити подібні, якщо є, і розкладати на множники:
Спробуй сам:
b) Знаменники містять літери
Пригадаймо принцип знаходження спільного знаменника без літер:
· Насамперед ми визначаємо загальні множники;
· Потім виписуємо всі загальні множники по одному разу;
· І домножуємо їх на всі інші множники, не спільні.
Щоб визначити спільні множники знаменників, спочатку розкладемо їх на прості множники:
Підкреслимо спільні множники:
Тепер випишемо спільні множники по одному разу і допишемо до них усі загальні (не підкреслені) множники:
- Це і є спільний знаменник.
Повернемося до букв. Знаменники наводяться за такою ж схемою:
· Розкладаємо знаменники на множники;
· Визначаємо загальні (однакові) множники;
· Виписуємо всі загальні множники по одному разу;
· Домножуємо їх на всі інші множники, не загальні.
Отже, по порядку:
1) розкладаємо знаменники на множники:
2) визначаємо загальні (однакові) множники:
3) виписуємо всі загальні множники по одному разу і примножуємо їх на всі інші (непідкреслені) множники:
Виходить, спільний знаменник тут. Перший дріб потрібно домножити на, другий – на:
До речі, є одна хитрість:
Наприклад: .
Бачимо в знаменниках одні і ті ж множники, тільки всі різними показниками. До спільного знаменника підуть:
у ступені
у ступені
у ступені
у ступені.
Ускладнимо завдання:
Як зробити у дробів однаковий знаменник?
Давай згадаємо основну властивість дробу:
Ніде не сказано, що з чисельника та знаменника дробу можна віднімати (або додавати) одне й те саме число. Тому що це не так!
Переконайся сам: візьми будь-який дріб, наприклад, і додай до чисельника і знаменника якесь число, наприклад, . Що повчилося?
Отже, чергове непорушне правило:
Коли наводиш дроби до спільного знаменника, користуйся лише операцією множення!
Але на що ж треба примножити, щоби отримати?
Ось на і домнож. А примножуй на:
Вирази, які неможливо розкласти на множники називатимемо «елементарними множниками». Наприклад, це елементарний множник. – теж. А ось – ні: він розкладається на множники.
Що скажеш щодо виразу? Воно елементарне?
Ні, оскільки його можна розкласти на множники:
(про розкладання на множники ти вже читав у темі «Розділ»).
Так ось, елементарні множники, на які ти розкладаєш вираз із літерами – це аналог простих множників, на які ти розкладаєш числа. І робитимемо з ними таким же чином.
Бачимо, що в обох знаменниках є множник. Він піде у спільний знаменник у мірі (пам'ятаєш, чому?).
Множник - елементарний, і він у них не загальний, значить перший дріб на нього доведеться просто примножити:
Ще приклад:
Рішення:
Перш ніж у паніці перемножувати ці знаменники, треба подумати, як їх розкласти на множники? Обидва вони представляють формули скороченого множення:
Чудово! Тоді:
Ще приклад:
Рішення:
Як завжди, розкладемо знаменники на множники. У першому знаменнику просто виносимо за дужки; у другому – різниця квадратів:
Здавалося б, спільних множників немає. Але якщо придивитися, то й так схожі… І справді:
Так і напишемо:
Тобто вийшло так: усередині дужки ми поміняли подекуди, і при цьому знак перед дробом помінявся на протилежний. Візьми на замітку, так робити доведеться часто.
Тепер приводимо до спільного знаменника:
Засвоїв? Зараз перевіримо.
Завдання для самостійного вирішення:
Відповіді:
Тут треба згадати ще одну – різницю кубів:
Зверніть увагу, що у знаменнику другого дробу не формула «квадрат суми»! Квадрат суми виглядав так: .
А – це так званий неповний квадрат суми: другий доданок у ньому – це твір першого та останнього, а не подвоєний їхній твір. Неповний квадрат суми – це один із множників у розкладанні різниці кубів:
Що робити, якщо дробів аж три штуки?
Та те саме! Насамперед зробимо так, щоб максимальна кількість множників у знаменниках була однаковою:
Зверніть увагу: якщо поміняти знаки всередині однієї дужки, знак перед дробом змінюється на протилежний. Коли міняємо знаки у другій дужці, знак перед дробом знову змінюється на протилежний. В результаті він (знак перед дробом) не змінився.
До загального знаменника виписуємо повністю перший знаменник, а потім дописуємо до нього всі множники, які ще не написані, з другого, а потім із третього (і так далі, якщо дробів більше). Тобто виходить так:
Хм... З дробами зрозуміло що робити. Але як бути з двійкою?
Все просто: адже ти вмієш складати дроби? Отже, треба зробити так, щоб двійка стала дробом! Згадуємо: дріб – це операція розподілу (числитель поділяється на знаменник, якщо ти раптом забув). І немає нічого простішого, ніж розділити число на. При цьому саме число не зміниться, але перетвориться на дріб:
Те що потрібно!
5. Множення та розподіл дробів.
Що ж, найскладніше тепер позаду. А попереду у нас найпростіше, але при цьому найважливіше:
Порядок дій
Який порядок дій при підрахунку числового виразу? Згадай, порахувавши значення такого виразу:
Порахував?
Повинно вийти.
Отже, нагадую.
Насамперед обчислюється ступінь.
Другим – множення та розподіл. Якщо множень і поділок одночасно кілька, робити їх можна у будь-якому порядку.
І наостанок виконуємо складання та віднімання. Знову ж таки, в будь-якому порядку.
Але: вираз у дужках обчислюється позачергово!
Якщо кілька дужок множаться або діляться один на одного, обчислюємо спочатку вираз у кожній із дужок, а потім множимо або поділи їх.
А якщо всередині дужок є ще одні дужки? Ну давай подумаємо: усередині дужок написаний якийсь вираз. А при обчисленні виразу насамперед треба робити що? Правильно, обчислювати дужки. Ну ось і розібралися: спочатку обчислюємо внутрішні дужки, потім решту.
Отже, порядок дій для вираження вище такий (червоним виділено поточне дію, тобто дію, яке виконую зараз):
Добре, це просто.
Але ж це не те саме, що вираз з літерами?
Ні, це те саме! Тільки замість арифметичних дій треба робити алгебраїчну, тобто дії, описані в попередньому розділі: приведення подібних, додавання дробів, скорочення дробів і так далі. Єдиною відмінністю буде дія розкладання багаточленів на множники (його часто застосовуємо під час роботи з дробами). Найчастіше для розкладання на множники потрібно застосовувати формули скороченого множення або просто виносити загальний множник за дужки.
Зазвичай наша мета – уявити вираз у вигляді твору чи приватного.
Наприклад:
Спростимо вираз.
1) Першим спрощуємо вираз у дужках. Там у нас різниця дробів, а наша мета – уявити її як твір чи приватний. Отже, наводимо дроби до спільного знаменника і складаємо:
Більше цього виразу спростити неможливо, всі множники тут – елементарні (ти ще пам'ятаєш, що це означає?).
2) Отримуємо:
Розмноження дробів: що може бути простішим.
3) Тепер можна і скоротити:
Ну от і все. Нічого складного, правда?
Ще приклад:
Спрости вираз.
Спочатку спробуй вирішити сам, і вже потім подивися рішення.
Насамперед визначимо порядок дій. Спочатку виконаємо складання дробів у дужках, вийде замість двох дробів один. Потім виконаємо поділ дробів. Ну і результат складемо з останнім дробом. Схематично пронумерую дії:
Тепер покажу звістку процес, підфарбовуючи поточну дію червоним:
Насамкінець дам тобі дві корисні поради:
1. Якщо є такі, їх треба негайно навести. У який би момент у нас не утворилися подібні, їх бажано наводити одразу.
2. Те саме стосується скорочення дробів: як тільки з'являється можливість скоротити, їй треба скористатися. Виняток становлять дроби, які ти складаєш або віднімаєш: якщо у них зараз однакові знаменникито скорочення потрібно залишити на потім.
Ось тобі завдання для самостійного вирішення:
І обіцяна на самому початку:
Рішення (короткі):
Якщо ти впорався хоча б із першими трьома прикладами, то тему ти, вважай, опанував.
Тепер уперед до навчання!
