Складання та віднімання алгебраїчних дробів. Додавання алгебраїчних дробів

Додаткові матеріали
Шановні користувачі, не забувайте залишати свої коментарі, відгуки, побажання. Усі матеріали перевірені антивірусною програмою.

Розвиваючі та навчальні посібники в інтернет-магазині "Інтеграл"
Посібник до підручника Муравіна Г.К. Посібник до підручника Макарічева Ю.М.

Що таке алгебраїчний дріб?

Алгебраїчна дріб - це вираз виду: $ \ frac (P) (Q) $.

Де:
P - чисельник алгебраїчного дробу.
Q - знаменник алгебраїчного дробу.

Наведемо приклади алгебраїчних дробів:

$\frac(a)(b)$, $\frac(12)(q-p)$, $\frac(7y-4)(y)$.

Основні властивості алгебраїчних дробів

Властивість 1.
І чисельник і знаменник дробу можна помножити на те саме число (або на одночлен, або на многочлен). У результаті, ми отримаємо той самий дріб, але представлений в іншому вигляді.

Інакше це перетворення називається тотожним. Його використовують, щоб привести алгебраїчне (і не тільки) вираз до більш простого вигляду, і робота з цим виразом буде зручнішою.

$\frac(a)(4b^2)=\frac(a*3b)(4b^2*3b)=\frac(3ab)(12b^3)$.

І чисельник та знаменник ми помножили на одночлен $3b$. У результаті у нас вийшов дріб, тотожний вихідний.

$\frac(a^2)(6b^3)=\frac(a^2*2)(6b^3*2)=\frac(2a^2)(12b^3)$.

За необхідності алгебраїчну дроб можна помножити на просте число. У цьому прикладі і чисельник і знаменник ми помножили на число 2. І знову ми отримали дріб, тотожний вихідний.

Властивість 2.
І чисельник, і знаменник дробу можна розділити на те саме число (або одночлен, або многочлен). У результаті ми отримаємо той самий дріб, але представлений в іншому вигляді.

Як і у випадку з множенням, до такого тотожного перетворення вдаються, щоб уявити дріб у більш простому виглядіта полегшити роботу з нею.

Додавання та віднімання алгебраїчних дробів з однаковими знаменниками

Якщо в алгебраїчних дробів однакові знаменники, їх складають як звичайні дроби (складають лише чисельники, а знаменник залишається загальним).

Загальне правило:

$frac(a)(d)+frac(b)(d)-frac(c)(d)=frac(a+b-c)(d)$.

приклад.

Спростіть вираз:

$\frac(2a^2+5)(a^2-ab)+\frac(2ab+b)(a^2-ab)-\frac(b+5)(a^2-ab)$.

Рішення.

Використовуємо правило додавання дробів про яке розказано вище, тобто складемо чисельники, а знаменник запишемо загальний.

$\frac(2a^2+5)(a^2-ab)+\frac(2ab+b)(a^2-ab)-\frac(b+5)(a^2-ab)=\frac ((2a^2+5)+(2ab+b)-(b+5))(a^2-ab)$.

Попрацюємо з чисельником.

$(2a^2+5)+(2ab+b)-(b+5)=$
$2a^2+5+2ab+b-b-5=2a^2+2ab$.

В результаті отримуємо дріб:

$\frac(2a^2+2ab)(a^2-ab)$.

Хлопці перед тим, як закінчити рішення, перевірте: чи не можна ще спростити отриманий результат. Адже в цьому полягає весь сенс перетворення – спростити вираз.
Якщо уважно подивитися, то можна зрозуміти, що отриманий дріб можна ще спростити.

$\frac(2a^2+2ab)(a^2-ab)=\frac(2a(a+b))(a(a-b))=\frac(2(a+b))(a-b)=\ frac(2a+2b)(a-b)$.

Додавання та віднімання алгебраїчних дробів з різними знаменниками

При додаванні алгебраїчних дробів з різними знаменникамитреба діяти як і, як із роботі з звичайними дробами. Спочатку треба привести дріб до спільному знаменнику, а потім скласти або відняти чисельники дробів, відповідно до загальним правиломМи розглянули.

приклад.
Обчисліть:

$\frac(a)(4b^2)+\frac(a^2)(6b^3)$.

Рішення.
Наведемо ці дроби до спільного знаменника. У цьому прикладі спільним знаменником є ​​одночлен $12b^3$.
Тоді.

$\frac(a)(4b^2)+\frac(a^2)(6b^3)=\frac(3ab)(12b^3)+\frac(2a^2)(12b^3)=
\frac(3ab+2a^2)(12b^3)$.

Найскладніше – це знаходження спільного знаменника для дробів. У деяких випадках це не просте завдання.
При знаходженні спільного знаменника можна дотримуватись правил:
1. Якщо обидва знаменники є одночленами без дужок, то краще спочатку підібрати загальний знаменник для числа, а потім - для змінної. У прикладі число - 12, а змінна - $b^3$.
2. Якщо знаменник є складнішим виразом, наприклад, $х + 1$, $x +y$ тощо, то краще підібрати знаменник у вигляді твору знаменників, наприклад, $(х + у)(х - у) $. Такий знаменник ділиться і на $х+у$, і на $х – у$.

Запам'ятайте!
Для двох алгебраїчних дробів спільних знаменників можна підібрати скільки завгодно. Але для спрощення розрахунків, потрібно вибрати найпростіший із можливих.

У цій статті ми детально розберемо складання та віднімання алгебраїчних дробів. Почнемо зі складання та віднімання алгебраїчних дробів з однаковими знаменниками. Після цього запишемо відповідне правило для дробів із різними знаменниками. На закінчення покажемо, як скласти алгебраїчну дріб із многочленом і як виконати їх віднімання. Всю інформацію за традицією забезпечимо характерними прикладами з роз'ясненням кожного кроку процесу розв'язання.

Навігація на сторінці.

Коли знаменники однакові

Принципи переносяться і на дроби алгебри. Нам відомо, що при додаванні та відніманні звичайних дробівз однаковими знаменниками складаються чи віднімаються їх чисельники, а знаменник залишається тим самим. Наприклад, і .

Аналогічно формулюється та правило складання та віднімання алгебраїчних дробів з однаковими знаменниками: щоб скласти або відняти алгебраїчні дроби з однаковими знаменниками, потрібно відповідно додати чи відняти чисельники дробів, а знаменник залишити без зміни.

З цього правила випливає, що в результаті складання або віднімання алгебраїчних дробів виходить новий алгебраїчний дріб (у окремому випадку багаточлен, одночлен або число).

Наведемо приклад застосування озвученого правила.

приклад.

Знайдіть суму алгебраїчних дробів 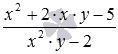та .

Рішення.

Нам потрібно скласти алгебраїчні дроби з однаковими знаменниками. Правило нам показує, що треба виконати складання чисельників цих дробів, а знаменник залишити тим самим. Отже, складаємо багаточлени , що перебувають у чисельниках: x 2 +2·x·y−5+3−x·y= x 2 +(2·x·y−x·y)−5+3=x 2 +x·y−2. Отже, сума вихідних дробів дорівнює .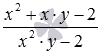

Насправді зазвичай рішення записується коротко як ланцюжка рівностей, відбивають все виконувані дії. У нашому випадку короткий запис рішення такий:

Відповідь:

.

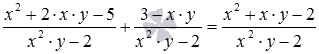Зауважимо, що й у результаті складання чи віднімання алгебраїчних дробів виходить скоротий дріб, його бажано скоротити.

приклад.

Виконайте віднімання з дробу алгебри дробу .

Рішення.

Оскільки знаменники алгебраїчних дробів рівні, то треба від числа числа першої дроби відняти чисельник другий, а знаменник залишити колишнім: .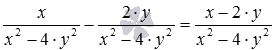

Неважко помітити, що можна виконати скорочення дробу алгебри . Для цього перетворимо її знаменник, застосувавши формулу різниці квадратів. Маємо.

Відповідь:

.

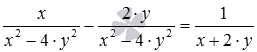Абсолютно аналогічно складаються або віднімаються три і більше алгебраїчних дробів з однаковими знаменниками. Наприклад, .

Додавання та віднімання алгебраїчних дробів з різними знаменниками

Нагадаємо, як ми виконуємо складання та віднімання звичайних дробів з різними знаменниками: спочатку наводимо їх до спільного знаменника, після чого складаємо ці дроби з однаковими знаменниками. Наприклад, або .

Існує аналогічне правило складання та віднімання алгебраїчних дробів з різними знаменниками:

• спочатку всі дроби наводяться до спільного знаменника;
• після чого виконується складання та віднімання отриманих дробів з однаковими знаменниками.

Для успішного застосування озвученого правила потрібно добре розібратися з приведенням алгебраїчних дробів до спільного знаменника. Цим і займемося.

Приведення алгебраїчних дробів до спільного знаменника.

Приведення алгебраїчних дробів до спільного знаменника є тотожне перетворення вихідних дробів, після якого знаменники всіх дробів стають однаковими. Зручно використати наступний алгоритм приведення алгебраїчних дробів до спільного знаменника:

• спочатку знаходиться загальний знаменник алгебраїчних дробів;
• далі визначаються додаткові множники для кожного дробу, для чого спільний знаменник ділиться на знаменники вихідних дробів;
• нарешті, чисельники та знаменники вихідних алгебраїчних дробів множаться на відповідні додаткові множники.

приклад.

Наведіть алгебраїчні дроби і до спільного знаменника.

Рішення.

Спочатку визначимо загальний знаменник алгебраїчних дробів. Для цього розкладаємо знаменники всіх дробів на множники: 2·a 3 −4·a 2 =2·a 2 ·(a−2), 3·a 2 −6·a=3·a·(a−2) та 4·a 5 −16·a 3 =4·a 3 ·(a−2)·(a+2). Звідси знаходимо спільний знаменник 12 · 3 · (a-2) · (a +2) .

Тепер приступаємо до знаходження додаткових множників. Для цього розділимо спільний знаменник на знаменник першого дробу (зручно взяти його розкладання), маємо 12·a 3 ·(a−2)·(a+2):(2·a 2 ·(a−2))=6·a·(a+2). Таким чином, додатковий множник для першого дробу дорівнює 6·a·(a+2) . Аналогічно знаходимо додаткові множники для другого та третього дробів: 12·a 3 ·(a−2)·(a+2):(3·a·(a−2))=4·a 2 ·(a+2)і 12·a 3 ·(a−2)·(a+2):(4·a 3 ·(a−2)·(a+2))=3.

Залишилося помножити чисельники та знаменники вихідних дробів на відповідні додаткові множники: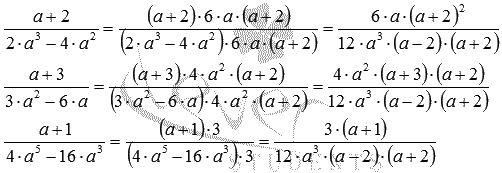

На цьому приведення вихідних дробів алгебри до спільного знаменника завершено. При необхідності отримані дроби можна перетворити на вид алгебраїчних дробів, виконавши множення багаточленів та одночленів у чисельниках та знаменниках.

Отже, з приведенням дробів алгебри до спільного знаменника розібралися. Тепер ми підготовлені до виконання додавання та віднімання алгебраїчних дробів з різними знаменниками. Так, мало не забули попередити: загальний знаменник до останнього моменту зручно залишати представленим у вигляді твору – можливо доведеться скорочувати дріб, який вийде після складання або віднімання.

приклад.

Виконайте складання алгебраїчних дробів та .

Рішення.

Очевидно, вихідні дроби мають різні знаменники, тому, щоб виконати їхнє складання, спочатку потрібно привести їх до спільного знаменника. Для цього розкладаємо знаменники на множники: x 2 +x=x·(x+1) , а x 2 +3·x+2=(x+1)·(x+2) , оскільки корінням квадратного тричлена x 2 + 3·x+2 є числа −1 та −2 . Звідси знаходимо спільний знаменник, він має вигляд x · (x + 1) · (x + 2). Тоді додатковим множником першого дробу буде x+2, а другого дробу – x.

Отже, і .

Залишилося скласти дроби, наведені до спільного знаменника: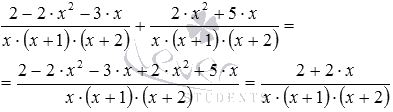

Отриманий дріб можна скоротити. Дійсно, якщо в чисельнику винести двійку за дужки, то буде видно загальний множник x+1, на який дріб і скорочується: .

Нарешті, отриманий дріб представляємо у вигляді алгебраїчної, для чого твір у знаменнику замінюємо багаточленом: .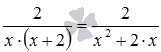

Оформимо коротке рішення, яке враховує всі наші міркування: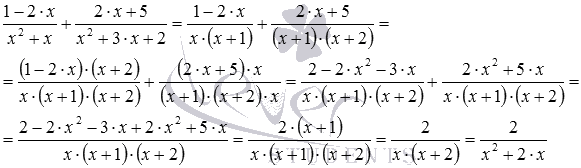

Відповідь:

.

І ще один момент: алгебраїчні дроби перед їх складанням або відніманням доцільно попередньо перетворити, щоб спростити, (якщо, звичайно, є така можливість).

приклад.

Виконайте віднімання алгебраїчних дробів та .

Рішення.

Виконаємо деякі перетворення алгебраїчних дробів, можливо, вони дозволять спростити процес розв'язання. Для початку винесемо за дужки числові коефіцієнти у змінних у знаменнику: 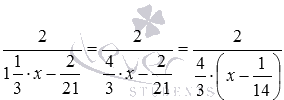і 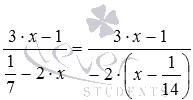. Вже цікаво – стало видно спільний множник знаменників дробів.

Тепер позбавимося числового коефіцієнта в знаменниках. На базі

Логічно перейти до розмови про діях з алгебраїчними дробами. З алгебраїчними дробами визначено такі дії: додавання, віднімання, множення, розподіл і зведення в натуральний ступінь. Причому всі ці дії замкнуті, в тому сенсі, що в результаті виконання виходить алгебраїчна дріб. Розберемо кожне їх по порядку.

Так, відразу слід зазначити, що дії з дробами алгебри є узагальненнями відповідних дій зі звичайними дробами. Тому відповідні правила практично дослівно збігаються з правилами виконання додавання та віднімання, множення, поділу та зведення в ступінь звичайних дробів.

Навігація на сторінці.

Додавання алгебраїчних дробів

Додавання будь-яких алгебраїчних дробів підходить під один із двох наступних випадків: у першому складаються дроби з однаковими знаменниками, у другому – з різними. Почнемо з правила додавання дробів з однаковими знаменниками.

Щоб скласти алгебраїчні дроби з однаковими знаменниками, потрібно додати чисельники, а знаменник залишити колишнім.

Озвучене правило дозволяє перейти від складання алгебраїчних дробів до складання багаточленів, що знаходяться в чисельниках. Наприклад, .

Для складання алгебраїчних дробів з різними знаменниками діяти потрібно за таким правилом: привести їх до спільного знаменника, після чого скласти отримані дроби з однаковими знаменниками.

Наприклад, при складанні алгебраїчних дробів і їх спочатку потрібно привести до спільного знаменника, в результаті вони набудуть вигляду. 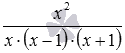і 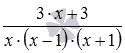відповідно, після чого виконується додавання цих дробів з однаковими знаменниками: .

Віднімання

Наступна дія – віднімання алгебраїчних дробів – виконується аналогічно до складання. Якщо знаменники вихідних алгебраїчних дробів однакові, потрібно просто виконати віднімання многочленов в чисельниках, а знаменник залишити колишнім. Якщо знаменники різні, то спочатку виконується приведення до спільного знаменника, після чого виконується віднімання отриманих дробів з однаковими знаменниками.

Наведемо приклади.

Виконаємо віднімання алгебраїчних дробів і їх знаменники однакові, тому . Отриманий дроб алгебри можна ще скоротити: .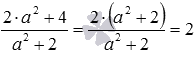

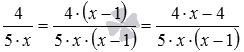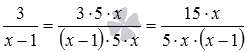Тепер віднімемо з дробу дріб. Ці алгебраїчні дроби з різними знаменниками, тому спочатку наводимо їх до спільного знаменника, який в даному випадку є 5·x·(x-1) , маємо і . Залишилося виконати віднімання: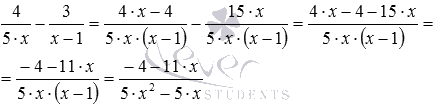

Розмноження алгебраїчних дробів

Алгебраїчні дроби можна множити. Виконання цієї дії проводиться аналогічно множенню звичайних дробів за таким правилом: щоб помножити дроби алгебри потрібно окремо перемножити чисельники, і окремо - знаменники.

Наведемо приклад. Помножимо алгебраїчну дріб на дріб. Відповідно до озвученого правила маємо 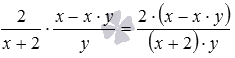. Залишилося отриманий дріб перетворити до алгебраїчного дробу, для цього в даному випадку потрібно виконати множення одночлена та багаточлена (а в загальному випадку - множення багаточленів) у чисельнику та знаменнику: .

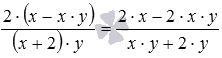Варто зауважити, що перед множенням алгебраїчних дробів бажано розкласти на множники багаточлени, що знаходяться в їх числах і знаменниках. Це пов'язано з можливістю скорочення дробу, що отримується. Наприклад,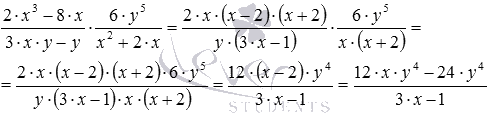

.

Більш детально цю дію розібрано у статті.

Поділ

Рухаємося далі за діями з дробами алгебри. На черзі – розподіл алгебраїчних дробів. Наступне правило зводить розподіл алгебраїчних дробів до множення: щоб розділити один алгебраїчний дріб на інший, потрібно перший дріб помножити на дріб, зворотний другий.

Під алгебраїчним дробом, зворотним до даного дробу, розуміється дріб з переставленими місцями чисельником і знаменником. Іншими словами, два алгебраїчні дроби вважаються взаємно зворотними, якщо їх твір тотожно дорівнює одиниці (за аналогією з ).

Наведемо приклад. Виконаємо поділ 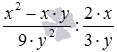. Дроб, зворотний дільнику, є. Таким чином, .

Для отримання більш детальної інформації звертайтеся до згаданої в попередньому пункті статті множення та розподіл алгебраїчних дробів.

Зведення алгебраїчного дробу до ступеня

Зрештою, переходимо до останньої дії з алгебраїчними дробами – зведення в натуральну міру. , а також те, як ми визначили множення алгебраїчних дробів, дозволяє записати правило зведення алгебраїчного дробу до ступеня: потрібно в цей ступінь окремо звести чисельник, і окремо – знаменник.

Покажемо приклад виконання цієї дії. Зведемо алгебраїчну дріб у другий ступінь. За наведеним правилом маємо . Залишилося звести у ступінь одночлен у чисельнику, а також звести у ступінь багаточлен у знаменнику, що дасть алгебраїчну дріб виду .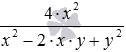

Рішення інших характерних прикладів показано у статті зведення алгебраїчного дробу до ступеня.

Список літератури.

• Алгебра:навч. для 8 кл. загальноосвіт. установ/[Ю. Н. Макарічев, Н. Г. Міндюк, К. І. Нешков, С. Б. Суворова]; за ред. С. А. Теляковського. - 16-те вид. - М.: Просвітництво, 2008. - 271 с. : іл. - ISBN 978-5-09-019243-9.
• Мордковіч А. Г.Алгебра. 8 клас. У 2 год. Ч. 1. Підручник для учнів загальноосвітніх закладів/А. Г. Мордкович. - 11-те вид., стер. – М.: Мнемозіна, 2009. – 215 с.: іл. ISBN 978-5-346-01155-2.
• Гусєв В. А., Мордкович А. Г.Математика (посібник для вступників у технікуми): Навч. посібник.- М.; Вищ. шк., 1984.-351 с., іл.

Copyright by cleverstudents

Всі права захищені.
Охороняється законом про авторське право. Жодну частину сайту, включаючи внутрішні матеріали та зовнішнє оформлення, не можна відтворювати в будь-якій формі або використовувати без попереднього письмового дозволу правовласника.

Відеоурок «Складання та віднімання алгебраїчних дробів з різними знаменниками» є наочним посібником, за допомогою якого дається теоретичний матеріал, докладно пояснюються алгоритми та особливості виконання операцій віднімання, складання дробів, що мають різні знаменники. За допомогою посібника вчителю легше сформувати вміння учнів виконувати операції з дробами алгебри. У ході відеоуроку розглядається ряд прикладів, розв'язання яких описується докладно, зважаючи на важливі деталі.

Застосування відеоуроку під час уроку математики дає можливість вчителю швидше досягти навчальних цілей, підвищити ефективність навчання. Наочність демонстрації допомагає учням запам'ятати матеріал, глибше його освоїти, тому відео можна використовувати, супроводжуючи пояснення вчителя. Якщо це відео використовується як частина уроку, то звільняється час вчителя посилення індивідуальної роботи та використання інших інструментів навчання підвищення ефективності навчання.

Демонстрація починається з представлення теми уроку. Зазначається, що виконання операцій віднімання, складання алгебраїчних дробів аналогічно до виконання операцій зі звичайними дробами. Нагадується механізм віднімання, складання для звичайних дробів - наводяться дроби до спільного знаменника, потім виконуються самі операції.

Озвучується та описується на екрані алгоритм віднімання, складання алгебраїчних дробів. Він складається з двох кроків - приведення дробів до однакових знаменників і потім виконання додавання (або віднімання) дробів з рівними знаменниками. Застосування алгоритму розглядається з прикладу знаходження значень виразів a/4b 2 -a 2 /6b 3 , і навіть x/(х+у)-x/(х-у). Зазначається, що для вирішення першого прикладу необхідно привести обидва дроби до одного знаменника. Цим знаменником буде 12b3. Приведення даних дробів до знаменника 12b 3 докладно розглядалося у минулому відеоуроку. В результаті перетворення виходить два дроби з рівними знаменниками 3ab/12b3 і 2a2/12b3. Ці дроби складаються відповідно до правила складання дробів із рівними знаменниками. Після складання чисельників дробів у результаті виходить дріб (3ab+2a 2)/12b 3 . Далі описується рішення прикладу х/(x+у)-x/(х-у). Після приведення дробів до одного знаменника виходять дроби (х 2 -ху)/(х 2 -у 2) та (х 2 +ху)/(х 2 -у 2). Відповідно до правила віднімання дробів з рівними знаменниками, робимо операцію з чисельниками, після чого виходить дріб -2ху/(х 2 -у 2).

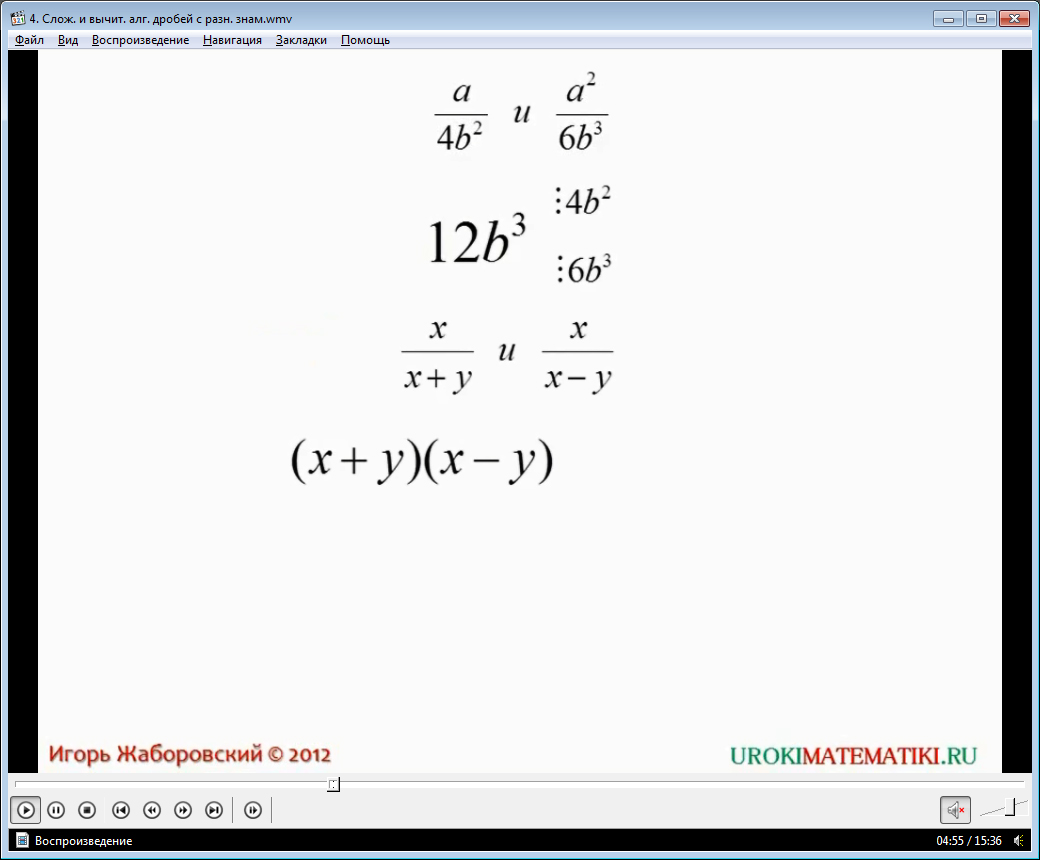
Зазначається, що найважчим кроком у вирішенні завдань на додавання, віднімання дробів, що мають різні знаменники, є приведення їх до спільного знаменника. Робляться підказки, як легко виробити навички у вирішенні цих завдань. Розбирається загальний знаменник дробу. Він складається з числового коефіцієнта зі змінною, зведеною до ступеня. Видно, що вираз може поділятися на знаменники першого та другого дробів. При цьому числовий коефіцієнт 12 є найменшим загальним кратним числових коефіцієнтів дробів 4 і 6. А змінну b містять обидва знаменники 4b 2 і 6b 3 . При цьому в загальному знаменнику міститься змінна найбільше серед знаменників вихідних дробів. Також розглядається знаходження спільного знаменника для х/(x+у) та x/(х-у). Зазначається, що спільний знаменник (x+у)(x-у) поділяється на кожен знаменник. Отже, вирішення завдання зводиться до знаходження найменшого загального кратного наявних числових коефіцієнтів, а також знаходження вищого показника ступеня для літерної змінної, що зустрічається кілька разів. Потім після збирання цих частин у загальний твір виходить спільний знаменник.

Озвучується і формулюється на екрані алгоритм знаходження кількох дробів загального знаменника. Цей алгоритм складається з чотирьох етапів, у першому з яких знаменники розкладаються на множники. На другому етапі алгоритму знаходиться найменше загальне кратне наявних даних коефіцієнтів, що входять до складу знаменників дробів. На третьому етапі складається твір, до складу якого входять літерні множники розкладів знаменників, у своїй літерний показник, що у кількох знаменниках, вибирається найбільшою мірою. На четвертому етапі числові та літерні множники, знайдені на попередніх етапах, збираються в один твір. Це буде спільний знаменник. До розглянутого алгоритму робиться зауваження. У прикладі знаходження загального знаменника дробів a/4b 2 і a 2 /6b 3 зазначається, що крім 12b 3 є інші знаменники 24b 3 і 48a 2 b 3 . І для кожної множини дробів можна знайти багато спільних знаменників. Однак знаменник 12b 3 є найпростішим і зручнішим, тому його називають найменшим загальним знаменником вихідних дробів. Додаткові множники є результатом приватного загального знаменника і вихідного знаменника дробу. Детально демонструється за допомогою анімації, як чисельник, знаменник дробів множиться на додатковий множник.

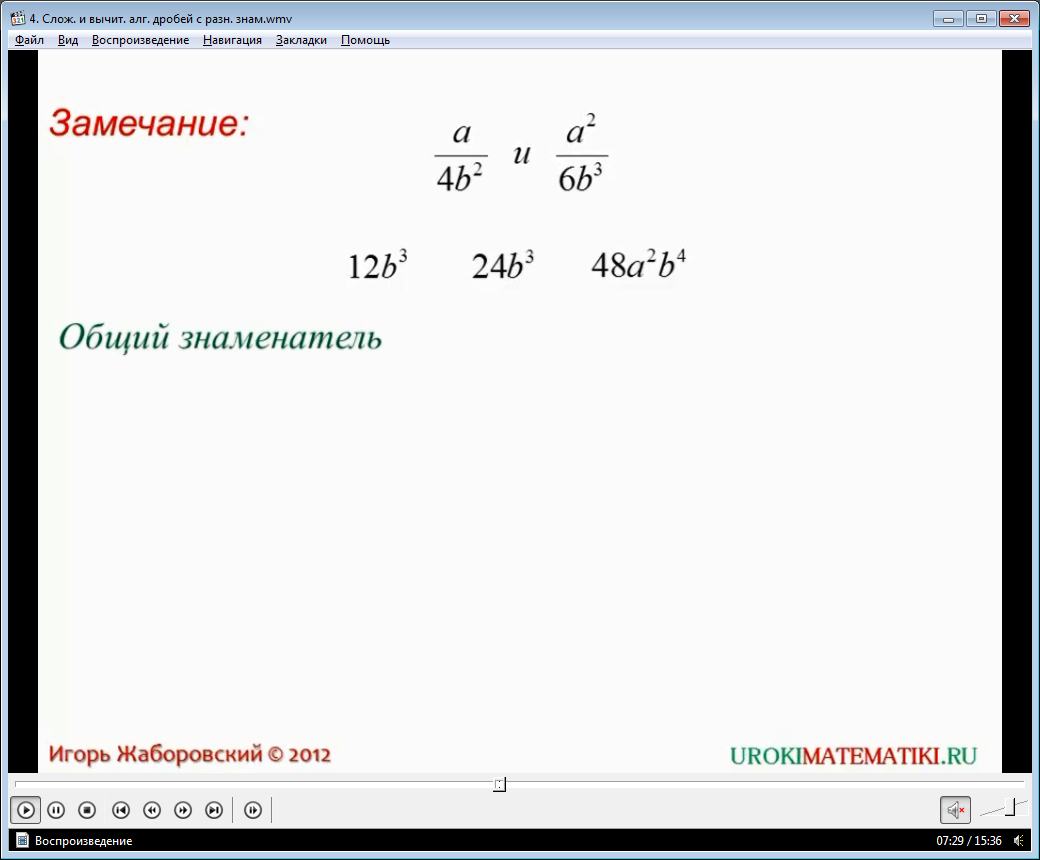
Далі пропонується розглянути алгоритм приведення до спільного знаменника алгебраїчних дробів у простішій формі, щоб він був зрозумілішим для учнів. Він також складається з чотирьох етапів, у першому з яких розкладання знаменників на множники. Потім пропонується з першого знаменника виписати всі множники, з інших знаменників добуток доповнити відсутніми множниками. Таким чином, знаходиться спільний знаменник. Знаходяться додаткові множники до кожного дробу з тих множників знаменника, що не потрапили до загального знаменника. Четвертим кроком є ​​визначення кожного дробу нового чисельника, що є твором старого чисельника і додаткового множника. Потім кожен дріб записується з новим чисельником та знаменником.

У наступному прикладі описується спрощення виразу 3а/(4а 2 -1)-(а+1)/(2а 2 +а). На першому етапі рішення знаменники кожного дробу розкладаються на множники. Для творів спільним множникомє (2а+1). Доповнивши твір множниками (2а-1) і а, виходить загальний знаменник виду а(2а-1)(2а+1). Будується допоміжна таблиця, у якій вказуються загальний знаменник, знаменники, додаткові множники. На другому етапі рішення кожен чисельник множиться на додатковий множник, виконується віднімання. В результаті виходить дріб (а 2-а+1)/а(2а-1)(2а+1).

У прикладі 3 розглядається спрощення виразу b/(2a 4 +4a 3 b+2a 2 b 2)-1/(3ab 2 -3a 3)+b/(6a 4 -6a 3 b). Рішення також розбирається за етапами, звертається увага на суттєві особливості виконання операцій, докладно описується приведення дробів до спільного знаменника, виконання операцій із чисельником. В результаті обчислень та після перетворення виходить дріб (2а 3 +6а 2 b-ab 2 +b 3)/6a 3 (a-b)(a+b) 2 .

Відеоурок «Складання та віднімання алгебраїчних дробів з різними знаменниками» може стати засобом підвищення ефективності уроку математики на цю тему. Посібник стане у нагоді вчителю, який здійснює дистанційне навчання, для наочного представлення навчального матеріалу. Учням відеоурок може бути рекомендованим для самостійного навчання, тому що в ньому докладно і зрозуміло пояснюються особливості виконання операцій, що вивчаються.

У даному уроці буде розглянуто додавання та віднімання алгебраїчних дробів з однаковими знаменниками. Ми вже знаємо, як складати і віднімати прості дроби з однаковими знаменниками. Виявляється, що алгебраїчні дроби підпорядковуються тим самим правилам. Уміння працювати з дробами з однаковими знаменниками є одним із наріжних каменів у вивченні правил роботи з дробами алгебри. Зокрема, розуміння даної теми дозволить легко освоїти складнішу тему - складання та віднімання дробів з різними знаменниками. У рамках уроку ми вивчимо правила складання та віднімання алгебраїчних дробів з однаковими знаменниками, а також розберемо цілий ряд типових прикладів

Правило складання та віднімання алгебраїчних дробів з однаковими знаменниками

Сфор-му-лі-ру-єм пра-ві-ло сло-же-ня (ви-чі-та-ня) ал-геб-ра-і-че-ських дро-бей з оди-на-ко-ви -ми зна-ме-на-те-ля-ми (воно сов-па-да-є з ана-ло-гіч-ним пра-ві-лом для звича-но-вен-них дрібниць): Тобто для сло-же-ня або ви-чи-та-ня ал-геб-ра-і-че-ських дро-бей з оди-на-ко-ви-ми зна-ме-на-те-ля-ми необ -хо-ді-мо зі-ста-вити со-від-віт-ству-ю-щу ал-геб-ра-і-че-ську суму чис-ли-те-лей, а зна-ме-на-тель залишити без змін.

Це правило ми розберемо і на прикладі звичайних дрібниць, і на прикладі алгебрійських дроків. бий.

Приклади застосування правила для звичайних дробів

Приклад 1. Складати дроби: .

Рішення

Сло-жим чис-ли-ті-ли дрібни, а зна-ме-тель залишимо таким же. Після цього раз-ло-жим чис-ли-тель і зна-ме-на-тель на прості про-мно-жи-те-лі і со-кра-тим. Променем: .

При-ме-ча-ня: стан-дарт-на помил-ка, ко-то-рую до-пус-ка-ють при розв'язанні подібного роду прикладів, за -клю-ча-є-ся в слі-ду-ю-щем спо-собі-рі-шення: . Це гру-бей-ша помилка, оскільки зна-мен-тель залишається таким же, яким був у вихідних дрібницях.

Приклад 2. Складати дроби: .

Рішення

Дана за-да-ча нічим не від-ли-ча-є-ся від попередньої: .

Приклади застосування правила для дробів алгебри

Від звичай-но-вен-них дробей пе-рей-дом до ал-геб-ра-і-че-ським.

Приклад 3. Складати дроби: .

Рішення: як уже го-во-ри-лося вище, сло-же-ня ал-геб-ра-і-че-ських дрібниць нічим не від-лі-ча-є-ся від сло- же-ня звичай-но-вен-них дрібниць. Тому метод розв'язання такий самий: .

Приклад 4. Вирахувати дроби: .

Рішення

Ви-чи-та-ня ал-геб-ра-і-че-ських дро-бей від-лі-ча-є-ся від сло-же-ня лише тим, що в чис-ли-тель за- пи-си-ва-є-ся різн-ність чис-ли-те-лей ви-хід-них дро-бей. По-це-му.

Приклад 5. Ви-честь дробу: .

Рішення: .

Приклад 6. Спростити: .

Рішення: .

Приклади застосування правила з наступним скороченням

У дробі, ко-то-рая по-лу-ча-ет-ся в ре-зуль-та-ті сло-же-ня або ви-чи-та-ня, мож-ни со-кра-ще- ня. Крім того, не варто за-бувати про ОДЗ ал-геб-ра-і-чеських дробей.

Приклад 7. Спростити: .

Рішення: .

При цьому . Во-обще, якщо ОДЗ ви-хідних дро-бей сов-па-да-ет з ОДЗ итого-вою, то його можна не вка-зи-вать (адже дріб, по-лу-чен- ная у від-ві-ті, також не буде сут-ство-вати при со-від-віт-ству-ють зна-че-ні-ях пере-мін-них). А от якщо ОДЗ вихідних дрібниць і відповіді не збігається, то ОДЗ вказувати необхідно.

Приклад 8. Спростити: .

Рішення: . При цьому y (ОДЗ ви-хідних дро-бей не сов-па-да-є з ОДЗ ре-зуль-та-та).

Додавання та віднімання звичайних дробів з різними знаменниками

Щоб склада-ти-вати і ви-читати ал-геб-ра-і-че-ські дроби з роз-ни-ми зна-ме-на-те-ля-ми, про-ве-демо ана-ло -гію з звичай-но-вен-ни-ми дро-бя-ми і пе-ре-не-сім її на ал-геб-ра-і-че-ські дроби.

Розглянув простий приклад для звичай-них дрібних.

Приклад 1.Складати дроби: .

Рішення:

Згадаймо пра-ві-ло сло-же-ня дрібниць. Для початку дробу необхідно привести до загального знамені. У ролі об-щого зна-ме-на-те-ля для звичай-но-вен-них дрібниць ви-сту-па-є найменше загальне кратне(НОК) ис-ход-них зна-ме-на-те-лей.

Опре-де-ле-ня

Найменше на-ту-раль-не число, яке де-літ-ся од-но-вре-мен-но на числа і .

Для нахо-дження НОК необхід-но-роз-ло-жити зна-ме-на-ті-лі на про-сті багато-жи-те-лі, а потім ви-брати все про- сті мно-жи-те-ли, ко-то-ры входять у раз-ло-же-ние обох зна-ме-на-те-лей.

; . Тоді в НОК чисел повинні входити дві двійки і дві трійки: .

Після знахо-дення об-ще-го зна-ме-на-те-ля, необ-хо-ди-мо для кож-ної з дро-бей знайти до-пов-ні-тель-ний багато- жи-тель (фак-ти-че-ськи, по-ділити загальний зна-ме-на-тель на зна-ме-на-тель зі-від-віт-ю-шої дробу).

Потім кожен дріб розумно-жа-ет-ся на по-лу-чен-ний до-пол-ні-тель-ний багато-жи-тель. По-лу-ча-ють-ся дроби з оді-на-ко-ви-ми зна-ме-на-те-ля-ми, склад-д-вати і ви-читати ко-то-рі ми на -вчилися на минулих уроках.

По-лу-ча-єм: .

Відповідь:.

Роз-див-рим тепер сло-же-ня ал-геб-ра-і-че-ських дро-бей з різн-ми-ми зна-ме-на-те-ля-ми. Сна-ча-ла роз-смот-рим дробу, зна-ме-на-те-ли ко-то-рих яв-ля-ють-ся чис-ла-ми.

Додавання та віднімання алгебраїчних дробів з різними знаменниками

Приклад 2.Складати дроби: .

Рішення:

Ал-го-ритм рішення аб-со-лют-но ана-ло-гі-чен пред-ду-ще-му при-ме-ру. Легко по-до-брати загальний зна-ме-на-тель дан-них дрібниць: і до-пол-ні-тель-ні багато хто для кожної з них.

.

Відповідь:.

Отже, сфор-му-лі-ру-єм ал-го-ритм сло-же-ня і ви-чи-та-ня ал-геб-ра-і-че-ських дро-бей з роз-ни-ми зна-ме-на-те-ля-ми:

1. Знайти най-менший загальний зна-ме-на-тель дро-бей.

2. Знайти до-пов-ні-тель-ні багато-ж-те-ли для кож-ної з дро-бей (поді-лів загальний зна-ме-на-тель на зна-ме-на-тель дан ного дробу).

3. До-мно-жити чис-ли-ті-ли на со-від-віт-стві-ю-щі до-пов-ні-тель-ні мно-жи-те-лі.

4. Складати або вирахувати дроби, користуючись пра-ві-ла-ми сло-же-ня і ви-чи-та-ня дрібни з оди-на-ко-ви-ми зна -Ме-на-те-ля-ми.

Роз-смот-рим те-пер приклад з дро-бя-ми, в зна-ме-на-те-лі ко-то-рих при-сут-ють бук-вен-ні ви-ра-же -Нія.