Дробові раціональні вирази є прикладами з рішеннями. Урок "перетворення раціональних виразів"

Тип уроку:урок закріплення знань.

Цілі уроку:

освітня- удосконалювати навички дій із раціональними дробами; формувати вміння виконувати тотожні перетворення раціональних виразів;
виховна- виховувати у школярів допитливість, почуття національної гордості, патріотизму; створення позитивного емоційного тла під час уроку;
розвиваюча– розвивати інтерес до математики та її історії, розвивати увагу, вчити проводити доказові міркування, використовуючи математичну мову; вивчати вміння зосереджуватися на навчальній діяльності та попереджати помилки щодо неуважності (розвивати самоконтроль); розвивати творчість учнів.

Етапи уроку

1. Організація початку заняття. Повідомлення теми та постановка мети.

2. Актуалізація опорних знань учнів.

3. Закріплення знань та способів дій.

4. Інформація про домашнє завдання, інструкція щодо його виконання. (Варіативне).

5. Підбиття підсумків уроку.

6.Рефлексія.

7. Фізкультурна хвилина (розвиток рухової сфери, гімнастика для очей).

Хід уроку

1. Організація початку заняття

Повідомлення теми та постановка мети. (Слайд №1)

Якщо ми відкриємо Великий Енциклопедичний словник, зможемо прочитати, що означає слово «перетворення». Отже, «Перетворення – заміна одного математичного об'єкта аналогічним об'єктом, що отримується з першого за певними правилами».

У Тлумачному Словнику Ожегова читаємо: «перетворити - зовсім переробити, перетворити з одного виду на інший, з однієї форми на іншу ..., змінити на краще».

Поясніть, будь ласка, навіщо потрібна заміна одного математичного об'єкта аналогічним йому об'єктом?

(Вислуховуються відповіді дітей.)

Т.ч. тотожні перетворення алгебраїчних виразів є набором методів, що дозволяють швидко і легко спростити складне вираження і привести його до більш компактного. Метою тотожних перетворень можливо приведення виразу до виду, зручнішому для чисельних розрахунків чи подальших перетворень.

Отже, сьогодні на уроці ми будемо вдосконалювати навички дій із раціональними висловлюваннями; формувати вміння виконувати їх тотожні перетворення.

2. Актуалізація опорних знань учнів

Діти, давайте згадаємо, які тотожні перетворення ми знаємо.

До тотожних перетворень відносяться:

приведення таких членів;
розкриття дужок;
розкладання на множники;
приведення алгебраїчних дробівдо спільного знаменника.

(На етапі актуалізації запропоновано кросворд на повторення теоретичних фактів, необхідних на уроці.)

У кожного з вас на парті лежить кросворд. Такий самий кросворд ви бачите на екрані. Вгадавши всі слова і записавши їх у клітинки по горизонталі, у виділеному вертикальному стовпці ви прочитаєте одне чудове слово. (Слайд №2)

(розгадавши кросворд, у виділеному вертикальному стовпці учні читають слово «істина»)

Чому мені захотілося виділити це слово? Тому що ми сьогодні познайомимося з фрагментами біографії однієї відомої жінки-математика, яка має девіз усього життя: «служити істині, служити справедливості». Але знайомитись ми будемо в результаті виконання навчальних завдань на тему сьогоднішнього уроку.

3. Закріплення знань та способів дій

1) (Слайд №3)

Хто ж ця жінка? Виберіть її ім'я з чотирьох імен відомих жінок, кожному з яких відповідає набір одиниць і нулів. Правильному відповіді питання відповідає набір, має деяке відмінне властивість проти іншими наборами.

Відповідь: С.В.Ковалевська. Набір (10111) відрізняється від трьох інших тим, що складається з чотирьох одиниць та нуля, а інші – з трьох одиниць та двох нулів.(Слайд №4)

Зазначимо коротко, чиї портрети, окрім С.В.Ковалевської, представлені на слайді.

(Довідка вчителя)

Додаток4

2) (Слайд №5)

Число, записане під роком народження С.В.Ковалевської, дорівнює кількості вірних рівностей серед наступних:

У кожного з вас на партах лежать картки зеленого та червоного кольору. Якщо ви вважаєте, що рівність правильна, то підніміть картку зеленого кольору, якщо - неправильне, то червоного.

Відповідь: Вірних рівностей чотири, рівність під буквою г) неправильне, порушено правило зведення дробу на ступінь.

(Слайд №6)

(Довідка вчителя)

3) Розглянемо приклади, що включають всі дії з дробами. Порядок їх виконання - такий самий, як і з числовими дробами. Існує два способи запису таких прикладів:

1) «ланцюжком» – для нескладних прикладів;

2) за процесами – для складніших. (Слайд №7)

Щоб дізнатися назву маєтку Крюковських, знайдіть значення виразу при х = 2, у = 5 і подайте відповідь у вигляді десяткового дробу:

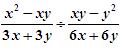
(Один учень біля дошки виконує завдання та записує приклад «ланцюжком»)

(Довідка вчителя)

(Слайд №8)

4) (Слайд №9)

Щоб дізнатись прізвище першого вчителя Софії Ковалевської, спростіть вираз.

(Один учень біля дошки виконує завдання та записує приклад «ланцюжком». Інші виконують завдання самостійно з подальшою перевіркою.)

(Довідка вчителя)

(Слайд №10)

5) (Слайд №11)

Щоб дізнатися ім'я петербурзького вчителя Софії Ковалевської, спростіть вираз і знайдіть його значення за х = -5 і у = 3.

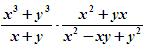
(Самостійна робота учнів з наступною перевіркою.)

Відповідь: 10

(Слайд №12)

(Довідка вчителя)

Фізкультурна хвилинка (розвиток рухової сфери, гімнастика для очей)

(Слайд №13)

6) (Слайд №14)

Порівняйте значення виразів А і В при р = -3,75 і ви дізнаєтеся ім'я знаменитого німецького математика, який став науковим керівником С. Ковалевської.

(Учні вирішують завдання за варіантами: 1 варіант знаходить значення виразу А, 2 варіант – вирази В. Два учні біля дошки виконують завдання, записуючи рішення за діями. Потім порівнюють відповіді.)

Відповідь: значення виразів А та В рівні.

(Довідка вчителя)

(Слайд №15)

7) (Слайд №16)

Чи знаєте ви, в якому університеті читала лекції та завідувала кафедрою С.В.Ковалевська?
Щоб дізнатися про це, розв'яжіть рівняння:

(З коментуванням з місця).

Відповідь: х = 10, х = -10.

(Довідка вчителя).

8) (Слайд №17)

Підберіть числа та запишіть їх у квадратних дужках так, щоб вийшло тотожність. Ви зможете дізнатися, в якій області С. В. Ковалевська була такою ж талановита, як і в математиці.

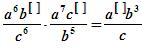
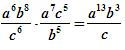
(Довідка вчителя)

(Слайд №18)

4. Інформація про домашнє (варіативне) завдання, інструкція про його виконання

Дано 3 різних варіанти домашнього завдання, кожному з вас пропонується вирішити один з них на вибір (завдання мають «підказку» - складність завдання).

5. Підбиття підсумків уроку

6. Рефлексія

Перед вами картка із зображенням гори. Якщо ви вважаєте, що тема уроку була цікавою, що добре і з користю попрацювали на уроці, дізналися щось нове, то намалюйте себе на вершині. високої гори. Якщо лишилося щось незрозуміло, намалюйте себе нижче.

Хочеться закінчити наш урок віршами Софії Ковалевської.

Якщо ти в житті, хоч на мить
Істину в серці своєму відчув,
Якщо промінь правди крізь морок і сумнів
Яскравим сяйвом твій шлях осяяв:
Щоб у вирішенні своєму незмінному
Рок не призначив тобі попереду
Пам'ять про цю мить священну
Вічно зберігай, як святиню, у грудях
Хмари зберуться громадою безладною,
Небо вкриється чорною імлою,
З ясною рішучістю, і з вірною спокійною
Бурю ти зустрінь і поміряйся з грозою.

Дякую за роботу!

(Слайд №19)

Ціле вираз - це математичне вираз, складене з чисел і літерних змінних за допомогою дій складання, віднімання та множення. Також до цілих відносяться висловлювання, які мають у своєму складі розподіл на якесь число, відмінне від нуля.

Нижче наведено кілька прикладів цілих виразів:

1. 12 * a 3 + 5 * (2 * a -1);

3. 4 * y- ((5 * y + 3) / 5) -1.

Якщо ж у виразі присутній розподіл на змінну або інше вираз містить змінну, то такий вираз не є цілим. Такий вираз називається дробовим. Дамо повне визначення дробового виразу.

Дробне вираз - це математичне вираз, яке крім дій додавання, віднімання та множення, виконаних з числами та буквеними змінними, а також поділу на число не рівне нулю, містить так само поділ на вирази з буквеними змінними.

Приклади дробових виразів:

1. (12 * a 3 + 4) / a;

3. 4*x – ((5*y + 3)/(5 – y)) + 1.

Дробові та цілі вирази становлять дві великі множини математичних виразів. Якщо ці множини об'єднати, то отримаємо нову множину, яка називається раціональними виразами. Таким чином, раціональні висловлювання - це все цілі та дробові вирази.

Одним з окремих випадків раціональних виразів буде дріб, чисельник і знаменник якого багаточлени. Для такого дробу в математиці теж існує своя назва - раціональний дріб. Раціональний дріб матиме сенс у тому випадку, якщо його знаменник не дорівнює нулю. Тобто допустимими будуть всі значення змінних, у яких знаменник дробу відмінний від нуля.

Перетворення раціональних виразів

Перетворення раціональних виразів завжди можна звести додавання, віднімання, поділу та множення раціональних дробів.
Як ми вже знаємо, суму, різницю, твір і приватний раціональний дроб завжди можна представити у вигляді деякої раціонального дробу.

Це безпосередньо випливає з правил проведення дій із дробами. З цього факту випливає, що будь-який раціональний вираз можна подати у вигляді раціонального дробу. Розглянемо наступний приклад перетворення раціонального виразу:

x + 1 - (1/(x + 2))*(x 2 - 4/x).

Першим дією виконаємо множення дробів:

(1/(x + 2))*(x 2 - 4/x) = (x 2 - 4)/((x + 2)*x) = ((x + 2)*(x - 2))/ ((x + 2) * x) = (x - 2) / x

Тепер віднімемо отриманий результат із многочлена (х + 1):

X + 1 - (x - 2) / x = (x * (x + 1) - (x - 2)) / x = (x 2 + x - x + 1) / x = (x 2 + 2) / x.

Таким чином, ми перетворили раціональний вираз на вигляд раціонального дробу.

Відповідь: x + 1 - (1 / (x + 2)) * (x 2 - 4 / x) = (x 2 + 2) / x.

На попередньому уроці вже було введено поняття раціонального вираження, на сьогоднішньому уроці ми продовжуємо працювати з раціональними висловлюваннями та основний упор робимо на їхнє перетворення. На конкретних прикладах ми розглянемо методи вирішення завдань на перетворення раціональних виразів та доказ пов'язаних із ними тотожностей.

Тема:Алгебраїчні дроби. Арифметичні операції над алгебраїчними дробами

Урок:Перетворення раціональних виразів

1. Раціональний вираз та методика його спрощення

Згадаймо спочатку визначення оптимального висловлювання.

Визначення. Раціональне вираз - алгебраїчний вираз, що не містить коріння і включає тільки дії додавання, віднімання, множення та поділу (зведення у ступінь).

Під поняттям «перетворити раціональне вираження» маємо у вигляді, передусім, його спрощення. А це здійснюється у відомому нам порядку дій: спочатку дії у дужках, потім добуток чисел(зведення в ступінь), розподіл чисел, а потім дії складання/віднімання.

2. Спрощення раціональних виразів із сумою/різністю дробів

Основною метою сьогоднішнього уроку буде набуття досвіду при вирішенні складніших завдань на спрощення раціональних виразів.

Приклад 1. Спростити раціональний вираз.

Рішення. Спочатку може здатися, що ці дроби можна скоротити, тому що вирази в чисельниках дробів дуже схожі на формули повних квадратів відповідних їм знаменників. В даному випадку важливо не поспішати, а окремо перевірити, чи це так.

Перевіримо чисельник першого дробу: . Тепер чисельник другий: .

Як видно, наші очікування не виправдалися, і вирази в чисельниках є повними квадратами, тому що у них відсутнє подвоєння твору. Такі вирази, якщо згадати курс 7 класу називають неповними квадратами. Слід бути дуже уважними у таких випадках, тому що переплутування формули повного квадрата з неповним – дуже часта помилка, а подібні приклади перевіряють уважність учня.

Оскільки скорочення неможливе, то виконаємо складання дробів. У знаменників немає спільних множниківтому вони просто перемножуються для отримання найменшого загального знаменника, а додатковим множником для кожного з дробів є знаменник іншого дробу.

Звичайно ж, далі можна розкрити дужки і привести потім подібні доданки, проте, в даному випадку можна обійтися меншими витратами сил і помітити, що в чисельнику перший доданок є формулою суми кубів, а друге - різниці кубів. Для зручності згадаємо ці формули у загальному вигляді:

У нашому випадку вирази в чисельнику згортаються наступним чином:

Друге вираження аналогічне. Маємо:

Приклад 2. Спростити раціональний вираз .

Рішення. Даний приклад схожий на попередній, але тут відразу видно, що в чисельниках дробів є неповні квадрати, тому скорочення на початковому етапі рішення неможливе. Аналогічно попередньому прикладу складаємо дроби:

Тут ми аналогічно способу, зазначеному вище, помітили та згорнули вирази за формулами суми та різниці кубів.

Приклад 3. Спростити раціональний вираз.

Рішення. Можна помітити, що знаменник другого дробу розкладається на множники за формулою суми кубів. Як ми знаємо, розкладання знаменників на множники є корисним подальшого пошуку найменшого загального знаменника дробів.

Вкажемо найменший загальний знаменник дробів, він дорівнює: , тому що ділиться на знаменник третього дробу, а перше вираз взагалі є цілим, і для нього підійде будь-який знаменник. Вказавши очевидні додаткові множники, запишемо:

3. Спрощення раціональних виразів зі складними багатоповерховими дробами

Розглянемо складніший приклад із «багатоповерховими» дробами.

Приклад 4. Довести тотожність при всіх допустимих значеннях змінної.

Доведення. Для доказу зазначеного тотожності намагатимемося спростити його ліву частину (складну) до того простого вигляду, Що від нас вимагається. Для цього виконаємо всі дії з дробами в чисельнику та знаменнику, а потім розділимо дроби та спростимо результат.

Доведено за всіх допустимих значень змінної.

Доведено.

На наступному уроці ми докладно розглянемо складні прикладина перетворення раціональних виразів.

Список літератури

1. Башмаков М. І. Алгебра 8 клас. - М: Просвітництво, 2004.

2. Дорофєєв Г. В., Суворова С. Б., Бунімович Є. А. та ін Алгебра 8. - 5-те вид. - М: Просвітництво, 2010.

3. Нікольський С. М., Потапов М. А., Решетніков Н. Н., Шевкін А. В. Алгебра 8 клас. Підручник для загальноосвітніх закладів. - М: Просвітництво, 2006.

1. Вчимося разом.

2. Розробка уроків, презентації, конспекти занять.

3. Інтернет-портал roman. by.

Домашнє завдання

1. №96-101. Дорофєєв Г. В., Суворова С. Б., Бунімович Є. А. та ін. Алгебра 8. - 5-те вид. - М: Просвітництво, 2010.

2. Спростіть вираз .

3. Спростіть вираз.

Відеоурок «Перетворення раціональних виразів» - наочний посібник щодо підсумкового уроку математики з відповідної теме. У результаті демонстрації узагальнюються основні методи перетворення раціональних висловів, докладно описуються приклади розв'язання завдань, у яких необхідно перетворити висловлювання. Даний посібник допоможе вчителю підвищити ефективність уроку математики, підсумувати безліч методів перетворення, знаходити найбільш доцільний спосіб розв'язання математичної задачі, в якій є раціональні висловлювання.

У відеоуроці використовуються методи, що покращують запам'ятовування матеріалу, що сприяють його розумінню. Для цього важливі поняття та особливості застосування методів вирішення завдань виділяються кольором та написанням, використовуються анімаційні ефекти. Оскільки відео доповнюється озвучуванням, можна вставити важливі коментарі. Таким чином, відеоурок стає важливим інструментом наочності та ефективним способомдосягнення навчальних цілей.

На початку уроку озвучується його назва. Зазначається, що це відео створено для підсумкового заняття, в якому поєднуються висновки, зроблені при вивченні чисел, степенях, багаточленах, степенях алгебри. У відеоуроці узагальнюються відомості, отримані про математичну мову, символи.

Учням нагадується, як розширювалися їхні знання про числа. На екрані показуються види чисел. Зазначається, що після вивчення цифр учні познайомилися з натуральними числамита правилами операцій над ними. Потім розкривалося поняття цілих чисел як множини натуральних, їм протилежних чисел і нуля. Потім вивчали раціональні числа, в які входять цілі числа та дроби. Розглядається приклад, що число 2 є натуральним, до того ж цілим та раціональним. Зазначається, що поняття раціональних чисел ширше, а ціле – вже. Найконкретніша назва даного числа- Натуральне. Далі вказується, будь-яке ціле число, наприклад, -2, то, можливо названо цілим і оптимальним. Але дріб, наприклад, 3/5 є лише оптимальним числом.

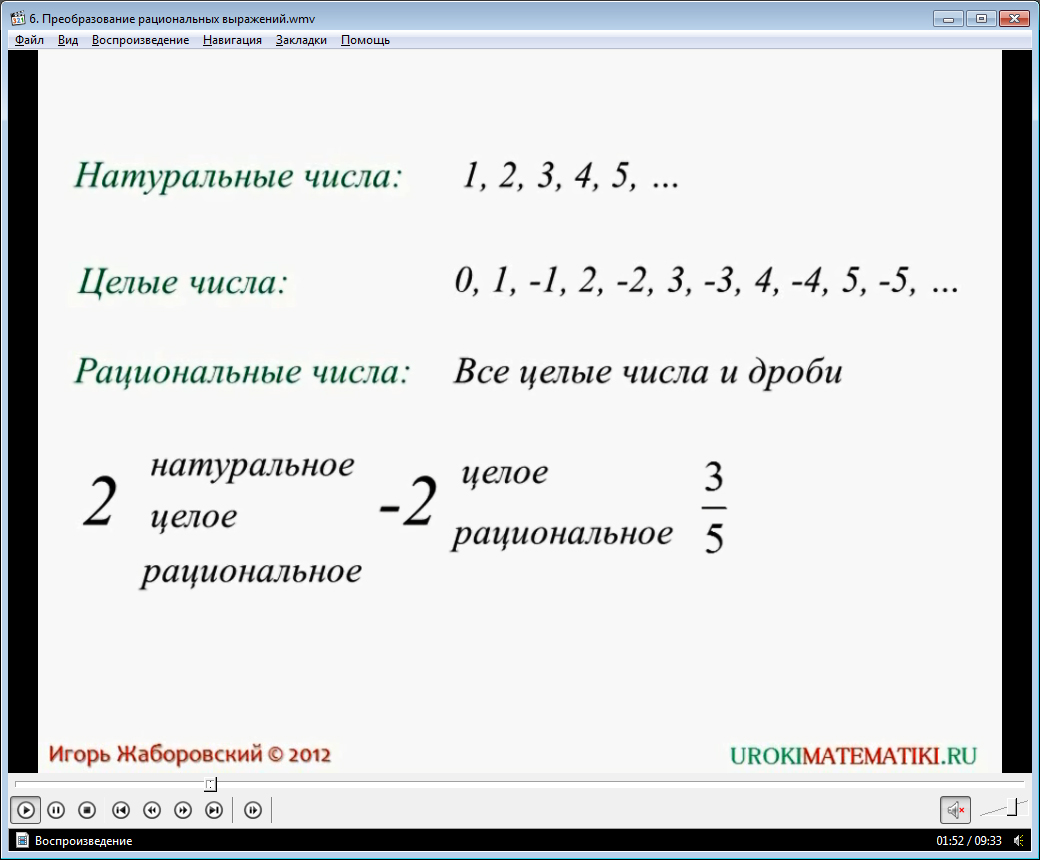
Далі розглядається вивчення алгебраїчних виразів. Зазначається, що першим етапом вивчення був рівень чисел, ступенів та змінних. Його аналогом у вивченні чисел було вивчення цифр. Потім за аналогією з натуральними числами у виразах вивчалися одночлени. Аналогічно цілим числам, вивчалися багаточлени, і як рівень раціональних чисел виступають алгебраїчні дроби. За допомогою кругової схеми розглядається, як розширюється поняття про вирази алгебри. У схемі зазначається, що числа, змінні та ступеня є окремим випадком одночленів, які в свою чергу - окремий випадокбагаточленів, які є частиною алгебраїчних дробів. Також вказується, що багаточлен - це ціле вираження, а алгебраїчний дріб є дробовим виразом. І будь-яке вираз алгебри після перетворення може перетворитися на алгебраїчну дріб.

Далі розглядається приклад, де необхідно довести справедливість тотожності. Учням нагадується, що довести тотожність означає встановити, що області допустимих значень частини тотожності рівні. Пропонується згадати види перетворень, які можуть допомогти довести тотожність. Це чотири методи:

права частина утворюється після перетворення лівої частини;
після перетворення правої частини виходить ліва частина;
перетворюються обидві частини тотожності, отримуючи однаковий результат;
становлять різницю частин, у своїй одержуючи нуль.

Зазначається, що з виборі способу вирішення завдання необхідно керуватися видом самого висловлювання. У прикладі доцільнішим є застосування першого способу. Вираз у лівій частині опису тотожності дуже складне. Для його перетворення використовується відоме правило порядку виконання операцій - спочатку перетворюється вираз у дужках, потім операції множення, поділу, а потім додавання та віднімання. Далі описуються дії, які необхідно виконати на вирішення завдання. Спочатку перетворюється вираз у дужках - два алгебраїчні дроби наводяться до спільному знаменнику, після чого виконується віднімання. Аналогічно виконується складання алгебраїчних дробів з різними знаменникамив інших дужках. Далі здійснюється розподіл дробів, отриманих результаті перетворення висловлювання в дужках. Четвертою дією є додавання дробів з рівними знаменниками. У результаті перетворень виходить вираз, що дорівнює виразу з правої частини. Таким чином, це тотожність вважається вірним. У цьому уточнюється область допустимих значень, у яких тотожність правильне. Такими значеннями для пари a, b будуть всі раціональні числа, крім знаменників, що звертають вихідних дробів в нуль. Відповідно, неприпустимі рівність 2a-b=0, 2a+b=0, b=0.

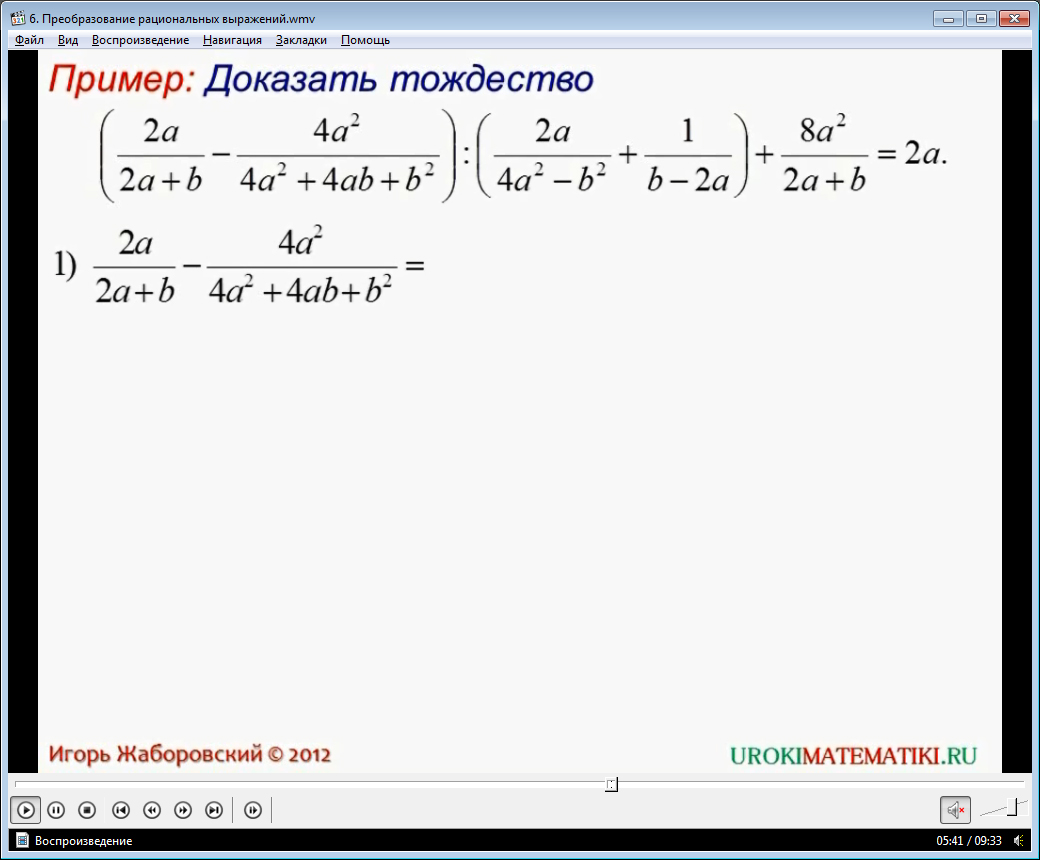
Відеоурок «Перетворення раціональних виразів» допоможе сформувати вміння перетворювати раціональні висловлювання на традиційному уроці математики у школі. Також цей матеріал може бути корисним вчителю для ведення дистанційних уроків. Учням, які вимагають додаткових занять, щоб опанувати тему, посібник може бути рекомендований для самостійної роботи.