Розкладання ступеня числа е в ланцюговий дріб. Дослідницька робота з математики "Ланцюгові дроби: прихована краса"

XXVIII науково-практична конференція

«Молоді уми – науці Красноярська»

«Ланцюгові дроби та їх застосування»

Дослідницька робота.

Пірматова Аліна Рустамбеківна,

учениця 11 Г класу

МБОУ ЦО №4

Науковий керівник:

Мустяця Олена Юріївна,

вчитель математики та інформатики

I кваліфікаційної категорії

м. Красноярськ-2015

Вступ
ГЛАВА I Теорія ланцюгових дробів
§1 Визначення ланцюгового дробу
§2 Обчислення відповідних дробів та їх застосування
РОЗДІЛ II Хід та результати дослідження
§1 Розв'язання рівнянь у цілих числах, різними методами
§2 Розв'язання рівнянь у цілих числах, за допомогою теорії ланцюгових дробів
Висновок
Література

ВСТУП

Навчаючись у випускному класі за системою прискореного навчання, переді мною постала проблема вибору форми складання іспиту з математики. Для того, щоб успішно скласти іспит на профільному рівні, необхідно вирішувати завдання не тільки першої, але другої його частини. Я звернулася до свого вчителя математики з наступним питанням: вирішення яких завдань допоможе мені здобути високий бал?

Виявляється, в останніх завданнях ЄДІ профільного рівня зустрічаються завдання на вирішення рівнянь та нерівностей у цілих числах. Вирішення такого завдання допоможе отримати додаткові бали. Мені було запропоновано розглянути питання використання теорії ланцюгових дробів для вирішення завдань другої частини іспиту.

Виходячи з вищесказаного, теманашої дослідницької роботи«Ланцюгові дроби та їх застосування».

Цільнашої роботи: дослідження теорії ланцюгових дробів як інструмент вирішення завдань ЄДІ профільного рівня.

Об'єктом дослідженняє ланцюгові дроби.

Предметом дослідження– ланцюгові дроби, як інструмент розв'язання рівнянь у цілих числах.

Гіпотеза дослідження: якщо вивчити теорію ланцюгових дробів та його застосування, можна навчитися вирішувати рівняння у цілих числах (від навчальних до олімпіадних).

Для досягнення мети дослідження та підтвердження висунутої гіпотези нами були сформульовані такі Завдання дослідження:

Вивчити теорію ланцюгових дробів.

Проаналізувати завдання другої частини ЄДІ кілька останніх років.

Співвіднести можливі способи розв'язання рівнянь у цілих числах із рішенням через використання теорії ланцюгових дробів.

База дослідження: типові завдання останнього завдання частини єдиного державного іспиту на профільному рівні – завдання на цілі числа.

ГлаваI

Ланцюгові дроби були введені в 1572 італійським математиком Бомбеллі. Сучасне позначення безперервних дробів зустрічається в італійського математика Катальді у 1613 році. Найбільший математик XVIII століття Леонардо Ейлер перший виклав теорію ланцюгових дробів, поставив питання їх використання на вирішення диференціальних рівнянь, застосував їх до розкладання функцій, уявленню нескінченних творів, дав важливе їх узагальнення.

Багато важливих результатів цієї теорії належать французькому математику Лагранжу, який знайшов метод наближеного рішення за допомогою ланцюгових дробів диференціальних рівнянь.

У сучасній математиці наближене уявлення функцій зазвичай розшукується як многочленів від незалежних змінних. У тих випадках, коли знаходження таких многочленів важко, зазвичай застосовуються різні чисельні методи.

При цьому порівняно рідко користуються наближеннями, що є дрібними. раціональними функціямивід незалежних змінних.

Тим часом дробово - раціональні наближення іноді можуть успішно замінювати цю функцію в тих галузях зміни аргументу, де розкладання цієї функції в статечний ряд розходиться і де, отже, наближення у вигляді багаточленів у більшості випадків непридатні.

Існують методи, що дозволяють отримувати скільки завгодно багато дробово-раціональних наближень даної функції та потребують складних викладок. Найбільш поширеним із таких методів є метод ланцюгових дробів.

Останнім часом виріс інтерес до ланцюгових дробів у зв'язку з їх великим теоретичним практичними значеннями.

Так, наприклад, ланцюгові дроби є одним з апаратів наближення функцій. Вони мають чудову властивість малого накопичення похибки при їх обчисленні.

В даний час підвищення інтересу до теорії ланцюгових дробів пояснюється ще й тим, що, незважаючи на видиму громіздкість уявлення, процес їх обчислень є циклічним і легко піддається програмуванню при використанні ЕОМ.

§1. Визначення ланцюгового дробу.

Ланцюговим дробом називається вираз виду:

Такий вираз називається правильним (кінцевим) ланцюговим або правильним безперервним дробом, при цьому передбачається, що ціле число, а , …, - натуральні числа.

Де числа q 1 , q 2 , q 3 , q 4 , …, називаються елементами ланцюгового дробу.

Ланцюговий дріб можна так само записати:

[q 1 , q 2 , q 3 … q n ]

Що значно спрощує запис.

Алгоритм Евкліда дає можливість знайти уявлення (або розкладання) будь-якого раціонального числа у вигляді ланцюгового дробу. Як елементи ланцюгового дробу виходять неповні приватні послідовні поділи в системі рівностей (1), тому елементи ланцюгового дробу називаються також неповними приватними. Крім того, рівності системи (2) показують, що процес розкладання в ланцюговий дріб полягає у послідовному виділенні цілої частини та перевертанні дробової частини.

Остання точка зору є більш загальною в порівнянні з першою, так як вона застосовна до розкладання в безперервний дріб не тільки раціонального, а й будь-якого дійсного числа.

Розкладання раціонального числа має, очевидно, кінцеве число елементів, оскільки алгоритм Евкліда послідовного поділу aна bє кінцевим.

Зрозуміло, кожен ланцюговий дріб представляє певне раціональне число, тобто дорівнює певному раціональному числу. Але виникає питання, чи є різні уявлення однієї й тієї ж раціонального числа ланцюговим дробом? Виявляється, що немає, якщо вимагати, щоб було .

Теорема. Існує один і тільки один кінцевий ланцюговий дріб, рівний даному раціональному числу, але за умови, що .

Доведення: 1) Зауважимо, що з відмови від зазначеного умови єдиність уявлення відпадає. Справді, при:

так що уявлення можна подовжити:

наприклад, (2, 3, 1, 4, 2) = (2, 3, 1, 4, 1, 1).

2) Приймаючи умову, можна стверджувати, що ціла частиналанцюгового дробу дорівнює її першому неповному приватному. Справді:

=

де 1, т.к.

Тому і тут. Доведемо те, що раціональне число однозначно є ланцюговим дробом якщо .

Нехай із умовою, . Тоді, отже. Повторним порівнянням цілих частин отримуємо , отже, тощо. Якщо, то продовження зазначеного процесу отримаємо також. Якщо ж, наприклад, то отримаємо , що неможливо.

Теорему доведено.

Зауваження:

Приклад: 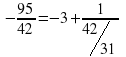, а так як , то .

Будь-яке ціле число можна розглядати як безперервний дріб, що складається з одного елемента.

Приклад: 5 = (5); .

Наведу кілька прикладів розкладання різних дробів та ірраціональних коренів у ланцюгові дроби:

приклад 1.Розкладемо звичайний дріб 105/38 у ланцюгову.

Включаємо алгоритм Евкліда.

105=38*2 +29

38=29*1 =9

29=9*3 +2

Неповні приватні (я їх спеціально наголосив) потрібно акуратно розташувати поспіль на поверхах ланцюгового дробу перед знаками плюс, замінюючи q. Отримаємо:

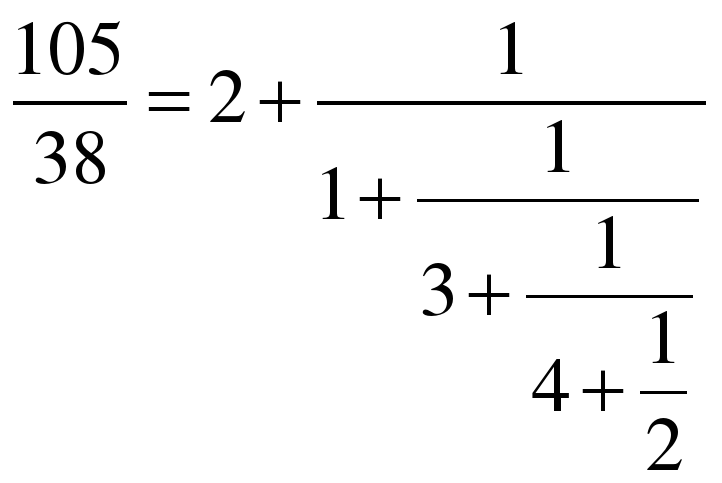
Або:

Приклад 2:Уявімо звичайний дріб 539/103 в ланцюгову.

Також за допомогою алгоритму Евкліда.

Отримаємо дріб:

Приклад 3:Уявімо звичайний дріб 1578/685 в ланцюгову.

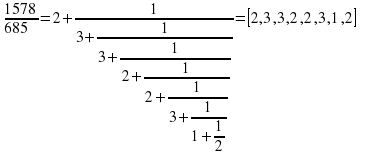
§2 Обчислення відповідних дробів.

В § 1 я показав, як перекладати звичайні дробиі ірраціональні числа в ланцюговий дріб, але частіше необхідно вирішити обернену задачу та обчислити величезну багатоповерховий дріб. Багато хто скаже, що це дуже довго і простіше не звертатися до ланцюгових дробів.

Насправді обчислювати ланцюговий дріб ще простіше, ніж переходити до нього, основну роль при цьому грають дроби виду:

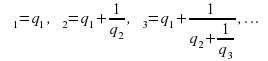або

Які називаються відповідними дробами даного безперервного дробу чи відповідного їй числа.

Зауважимо, що = =. Вважається, що відповідний дріб має порядок k .

Перш ніж приступити до обчислення відповідних дробів зауважимо, що переходить у , якщо в першому замінити виразом .

При цьому приймається, що , (це просто угода, не лякайтеся на нуль ніхто не збирається ділити), , , , і так далі.

Закономірність, яку ми помічаємо в побудові формули (її чисельника і знаменника ), зберігається при переході до і збережеться також при переході від kдо ( k +1).

Тому, на підставі принципу математичної індукції, для будь-якого k, де , маємо

Отримали дві формули, якими користуватимемося для обчислення ланцюгових дробів.

Обчислювати дроби дуже зручно, використовуючи таблицю.

Приклад 4

Обчислимо розкладений раніше в Прикладі 1 дріб:

P o = 1 Q o = 0 P 1 = q 1 Q 1 = 1

P 2= 1*2+1=3 Q 2= 1*1+0=1

P 3= 3*3+2=11 Q 3= 3*1+1=4

P 4= 4*11+3=47 Q 4= 4*4+1=17

P 5 = 2 * 47 +11 = 105 Q 5 = 2 * 17 +4 = 38

Звідси бачимо, що,

а - і є шукане число.

k	0	1	2	3	4	5
q k
P k
Q k

Приклад 5

Обчислимо розкладений раніше в Прикладі 3 дріб:

Дуже часто необхідно спочатку перевести число в ланцюговий дріб, а потім порахувати такі приклади в мене представлені в додатку.

За допомогою ланцюгових дробів так само вирішувати рівняння та завдання, які необхідно вирішити у цілих числах.

Приклад 6 (рівняння):

142x +82y =6 /:2

Дане рівняння рівносильне рівнянню:

71x +41y =3

Розкладемо 71/41 у ланцюговий дріб

Складемо таблицю відповідних дробів:

k	0	1	2	3	4	5	6	7
q k
P k
Q k

На підставі якості відповідних дробів

Помноживши обидві частини на 3 знаходимо:

тобто. х 0 =-45, у 0 = 78 - приватне рішення даного рівняння.

Усі рішення можуть бути знайдені за формулами:

x = -45 + 41t y = 78-71t

де t приймає будь-які цілі значення.

Приклад 7:

Розв'язати рівняння у цілих числах:

7k -20n = 5

Розкладемо в ланцюговий дріб:

Складемо таблицю відповідних дробів

K	0	1	2	3	4
q k
P k
Q k

За якістю відповідних дробів:

Усі рішення можуть бути знайдені за такою формулою:

де t- всі цілі значення

Приклад 8 (завдання):

Транспортної організації, що має вантажні автомашини вантажопідйомністю 3,5 і 4,5т, запропоновано перевезти 53т вантажу. Визначимо, скільки вантажних автомашин повинен виділити диспетчер транспортної організації для перевезення зазначеного вантажу одним рейсом за умови повного використання вантажопідйомності всіх машин.

Нехай х - число машин вантажопідйомністю 3,5т, що виділяються, у - число машин вантажопідйомністю 3,5т, що виділяються. Для отримання відповіді необхідно вирішити рівняння

у цілих числах з урахуванням того, що

Рівняння (1) рівносильне рівнянню 7х+9у=106

Підрахуємо відповідні дроби.

K	0	1	2	3	4
q k
P k
Q k

За властивістю відповідних дробів

Розв'язаннями рівняння будуть:

де t – будь-яке ціле число.

Тепер із всіх рішень виберемо невід'ємні:

Нехай t =-47, отже Х=424+9(-47)=1 та Y=-318-7(-47)=11.

Відповідь: х = 1, у = 11.

ГлаваII . Хід та результати дослідження

§1 Розв'язання рівнянь у цілих числах, різними методами

Лінійні рівняння в цілих числах можуть бути:

Метод прямого перебору

Використання нерівності

Використання відношення подільності

Виділення цілої частини

Метод залишків

Метод «спуску»

Метод послідовного зменшення коефіцієнтів за модулем

Використання формул

Використання кінцевих ланцюгових дробів

Приклад №75

Розв'язати у натуральних числах рівняння:

Метод: Використання нерівностей

Вирішення: Для зменшення перебору варіантів розглянемо нерівності

(5x =39-8y ≥0 (y ≤4

(8y =39-5x ≥0 (x ≤7

Проведемо перебір за невідомою у:

Якщо у = 1, то х = 6,2 не є натуральним числом.

Якщо у = 2, то х = 4,6 не є натуральним числом.

Якщо у = 3, то х = 3.

Якщо у = 4, то х = 1,4 не є натуральним числом.

Відповідь: (3;3)

Приклад №76

Є контейнери двох видів: по 130 кг та 160 кг. Скільки було контейнерів першого та скільки другого виду, якщо разом вони важать 3 тонни? Вкажіть усі рішення.

Метод: Використання відношення подільності

Рішення: Позначимо кількість контейнерів першого виду через х, другого через у. Отримуємо рівняння 130х +160у = 3000 або 13х +16у = 300

13х+13у+3у=13*23+1

3у-1 = 13 (23-х-у)

Звідси випливає, що різницю 3у-1 поділяється на 13.

Якщо 3у-1=0, то не є натуральним числом.

Якщо 3у-1=13, то не є натуральним числом.

Якщо 3у-1 = 26, то у = 9 і х = 12.

Якщо 3у-1=39, то не є натуральним числом.

Якщо 3у-1=52, то не є натуральним числом.

Якщо 3у-1 = 65, то у = 22, але 16 * 22 = 352300.

Відповідь: 12 контейнерів по 130 кг та 9 по 160 кг.

Приклад№77

У восьминога 8 ніг, а у морських зірки 5. Скільки в акваріумі тих та інших, якщо всього у них 39 ніг?

Метод: Виділення цілої частини

Рішення: Нехай х-кількість восьминогів, у-кількість морських зірок, тоді отримуємо рівняння 8х +5у = 39

Виразимо з рівняння і виділимо цілу частину:

Звідси випливає, що різниця 3-4 ділитися на 5.

Якщо 3х-4 = 0, то х не є натуральним числом.

Якщо 3х-4=5, то х=3 та у=3.

Якщо 3х-4 = 10, то х не є натуральним числом.

Якщо 3х-4=15, то не є натуральним числом.

Якщо 3х-4 = 20, то х = 8, але 8 * 8 = 6439.

Відповідь: 3 та 3.

Зауваження: У двох останніх прикладах використано відношення подільності, при цьому рівняння наводилися до різного вигляду. У цих прикладах зменшення перебору варіантів можна було додатково використовувати нерівності.

Приклад №78

Розв'язати у цілих числах рівняння 3х-4у=1.

Метод: Залишків

Рішення: Перепишемо рівняння у вигляді 3х = 4у +1. По скільки ліва частина рівняння ділиться на 3, то має ділитися на 3 і права частина. Розглянемо три випадки.

1. Якщо у = 3m, де m € Ƶ, то 4у +1 = 12m +1 не ділиться на3.

2.Если у = 3m +1, то 4у +1 = 4 (3m +1) +1 = 12m +5 не ділиться на3.

3.Якщо у = 3m +2, то 4y +1 = 4 (3m +2) +1 = 12m +9 ділиться на 3, тому 3х = 12m +9, х = 4m +3.

Відповідь: х = 4m +3, у = 3m +2 де m € Ƶ

Приклад №79

Вирішити в цілих числах рівняння 5х-7у = 3

Метод: "Спуску"

Рішення: Виразимо з рівняння те невідоме, коефіцієнт при якому менший за модулем:

Дроб 2у+3 повинен дорівнювати цілому числу.

Покладемо 2у + 3 Z, де Z - ціле число.

Тоді 2у +3 = 5z. З останнього рівняння висловимо те невідоме, коефіцієнт при якому менший за модулем, і проробимо аналогічні перетворення:

5z -3 z +3

Дроби z +2 повинні дорівнювати цілому числу.

Позначимо z +2 = t, де t – ціле число. Звідси z = 2t -3. Послідовно

повертаємося до невідомих х і у:

у = 3 (2t -3) -t = 5t -9,

х = у + z = 5t -9 +2t -3 = 7t -12/

Відповідь: х = 7t -12, y = 5t -9 де t € Ƶ.

Приклад №80

Вирішити в цілих числах рівняння 79у-23х = 1

Метод: Послідовного зменшення коефіцієнтів за модулем.

Рішення: Проведемо розподіл із залишком 79=23*3+10 і перепишемо вихідне рівняння у вигляді: 23х=79у-1=69у+10у-1,

23х-69у = 10у-й.

Ліва частина останнього рівняння ділиться націло на 23, тому і права частина повинна ділитися на 23. Маємо 10у-1=23t, де t€?

Для отриманого нового рівняння повторимо процедуру зменшення коефіцієнта. 10y = 23t +1 = (2 * 10 +3) t +1;

10y -20t = 3t +1; 3t +1 = 10u, де u € Ƶ.

Виразимо х і у через n. Оскільки u =3n +1, то

3t=10u-1=10(3n+1)-1=30n+9;

t=10n+3

10y=23t+1=23(10n+3)+1=230n+70;

y=23n+7.

23x=79y-1=79(23n+7)-1=79*23n+552;

x = 79n +24.

Відповідь: х = 79n +24; y = 23n +7 де n € Ƶ.

§2Розв'язання рівнянь у цілих числах, за допомогою теорії ланцюгових дробів

Розглянемо приклади з попереднього параграфа, розв'язавши їх за допомогою теорії ланцюгових дробів.

Приклад №75

5x +8y = 39

Складемо ланцюговий дріб

1) 5 0 + 1

8 1 + 1

1 + 1

1 + 1

2) 5=8*0+5

8=5*1+3

5=3*1+2

3=2*1+1

q k
P k
Q k

2=1*2

3) 3*5-8*2= (-1) 3

3*5-8*2= -1 / *(-1)

8*2+5*(-3)=1 / *39

8*78+5*(-117)=39

x o = 78 y o = -117

x = 78+5t

y=-117-8t

(78+5t ≥0, (5t ≥-78, t ≥-15,6

(-117-8t ≥0, (-8t ≥117, t ≤-14,625)

Відповідь: х = 78-75 = 3

у=-117+120=3 де t € Ƶ

Приклад №76

130x +16y = 3000,

13x +16y = 300,

Складемо ланцюговий дріб

1) 13 0 + 1

2) 13=16*0+13,

16=13*1+3, Складемо таблицю відповідних дробів

q k
P k					13
Q k					16

13=3*4+1,

З властивостей відповідних дробів випливає

3) 4*16-13*5= (-1) 4-1

4*16-13*5= -1 / * (-1)

13*5+16*(-4)=1 / *300

13*1500+16*(-1200)=300

Тобто приватне рішення має вигляд

x o = 1500 y o = -1200

x = 1500+16t

y = -13t - 1200

Так як Х і У можуть бути тільки позитивні то

(1500+16t ≥0, (16t ≥-1500, (t ≥-93,75, (x =1500+16*(-93)), (x =1500-1488, (x =12,

(-13t -1200≥0, (-13t ≥1200, (t ≤-92(4/13), (y =-13*(-93)=1200), (y =1203-1200, (y =9)).

Відповідь: 12 та 9 де t € Ƶ

Приклад №77

1) 8*х+5у=39, де х0 та у0

8 1

5 = + 1

1 + 1

1 +

P2=q2* Р1+ Р0=1*1+1=2 Q2= q2* Q1 +Q0 =1*1+=1

P3 = q3 * Р2 + Р1 = 1 * 2 +1 = 3 Q3 = q3 * Q2 + Q1 = 1 * 1 +1 = 2

P4 = q4 * Р3 + Р2 = 2 * 3 +2 = 8 Q4 = q4 * Q3 + Q2 = 2 * 2 +1 = 5

4) 3*5-8*2=(-1) ,

3*5-8*2= -1 /(-1)

8*2+5*(-3)=1 /* 39,

8*78+5*(-117)=39

XO = 78, У O = -117

5) Рішення рівняння буде:

х = 78 +5 t

Y=-117-8 t, де tcz

(78+5 t0, (5 t-78, t-15,6,

(-117-8 t0, (-8 t117, t

t=-15

x = 78-75 = 3

y = -117 +180 = 3 Відповідь: 3 і 3

Приклад №78

1) 3х-4у = 1

Складемо ланцюговий дріб

3 0 + 1

2) 3=4*0+3

1=1*1 Складемо таблицю відповідних дробів

q k
P k
Q k

З властивостей відповідних дробів випливає

3) 2*4-3*3=(-1) 3

2*4-3*3= -1 / *(-1)

3*3-4*2=1 / 1

Тобто приватне рішення має вигляд

x o = 3 y o = 2

Відповідь: x =3+4t

у=2+3t де t € Ƶ

Приклад №79

5x -7y = 3

Складемо ланцюговий дріб

1) 5 = 0 + 1

7 1 + 1

2) 5=7*0+5 Складемо таблицю відповідних дробів

q k
P k
Q k

7=5*1+2

5=2*2+1

2=1*2

З властивостей відповідних дробів випливає

3) 2*7-5*3= (-1) 3

2*7-5*3=-1 / *(-1)

5*3+2*(-7)= / *3

5*8-7*6=3

Тобто приватне рішення має вигляд

x o = 9 y o = 6

Відповідь: x=9+7t

y =6+5t де t € Ƶ

Приклад №80

1) 79у-23х = 1

Складемо ланцюговий дріб

2) 79=23*3+10

Складемо таблицю відповідних дробів

qk
Pk				24	79
Qk					23

P 2= q 2* P 1 +P 0= 2*3+1=7 Q 2= q 2* Q 1+ Q 0= 2*1+0=2

P 3= q 3* P 2+ P 1= 3*7+3=24 Q 3= q 3* Q 2+ Q 1= 3*2+1=7

P 4= q 4* P 3 +P 2= 3*24+2=79 Q 4= q 4* Q 3+ Q 2= 3*7+2=23

З властивостей відповідних дробів випливає

3) 24*23-79*7= (-1) 3

24*23-79*7= -1 / *(-1)

79*7+24*(-23)=1 / *1

Тобто приватне рішення має вигляд

x 0 = 7 y 0 = 24

Відповідь: х=7+23t

y =24+79t де t €?

Висновок

У роботі розглядається дуже цікаве математичне поняття ланцюговий дріб. Широкого практичного застосуваннявони не отримали, тому що для них немає зручних правил виконання арифметичних дійякі є для десяткових дробів. Але їх перевагою є те, що їхні властивості не пов'язані ні з якою системою числення. Тому ланцюгові дроби ефективно використовуються в теоретичних дослідженнях. Виклад матеріалу, що представлено в даній роботі, принципово відрізняється від тих публікацій, з якими працював автор, як за логікою викладу, доступності, великою кількістю практичних завдань та прикладів, що показують застосування ланцюгових дробів та оригінальність вирішення звичних задач.

У другому розділі нашої дослідницької роботи можна помітити наскільки зручним виявився спосіб розв'язання, лінійних рівнянь із двома невідомими. Для порівняння нами представлені рішення цих завдань різними методами, які мають на увазі, що учень повинен мати пристойний «багаж знань». Порівнюючи розглянуті методи з рішеннями через використання теорії ланцюгових дробів і властивостей відповідних дробів, видно зручність та універсальність розглянутого способу розв'язання.

Таким чином, мету нашого дослідження досягнуто частково, оскільки ми розглянули досить вузьке коло завдань, що зустрічаються в ЄДІ з математики на профільному рівні. Проте висунута гіпотеза повністю підтвердилася.

Література

В.О. Бугаєнко. Рівняння Пелля. - МЦНМО, 2002.

В.І. Арнольд. Ланцюгові дроби. – МЦНМО, 2002.

Математична енциклопедія, том V, М, «Радянська енциклопедія», 85.

Ш.Х. Михелович. Теорія чисел. М, "Вища школа", 67.

А.А. Бухштаб. Теорія чисел. М, "Освіта", 96.

Г.Д. Балки. Математика після уроків. М, "Освіта", 71.

А.А. Кочів. Задачник-практикум з алгебри та теорії чисел. М, "Освіта", 84.

О.С. Ляпін, А.Є. Євсєєв. Алгебра та теорія чисел. М, "Освіта", 74.

Л.Я. Куликов, А.І. Москаленко, О.О. Фомін. Збірник завдань з алгебри та теорії чисел. М, "Освіта", 93.

І.М. Виноградів. Основи теорії чисел. М, "Наука", 72.

Алгебра та теорія чисел. За редакцією Н.Я. Віленкіна, М, «Освіта»,

Математика ЄДІ 2011 (типові завдання С6). Завдання на цілі числа (від навчальних завдань до олімпіадних) Корянов А.Г. та Прокоф'єв А.А.

Чисельники

Бубнова Вікторія

Дослідницька робота з математики "Ланцюгові дроби: прихована краса" присвячена історії ланцюгових дробів, їх графічному уявленню - фраклалам, застосуванню ланцюгових дробів у житті.

У ході роботи над проектом було встановлено зв'язок між ланцюговими дробами та рекурсією у програмуванні, написані програми мовою Pascal для переведення ланцюгових дробів у десяткові та назад.

Робота зайняла І місце на шкільній науково-практичній конференції, ІІ на районній конференції школярів з математики, ІІІ місце на Всеросійському Вахтерівському фестивалі-конкурсі "Краса та велич математики".

Завантажити:

Попередній перегляд:

Щоб користуватися попереднім переглядом презентацій, створіть собі обліковий запис Google і увійдіть до нього: https://accounts.google.com

Підписи до слайдів:

МУНІЦИПАЛЬНА БЮДЖЕТНА ОСВІТАЛЬНА УСТАНОВА «Середня школа №15» м. Заволжжя Дослідницький проект з математики «Ланцюгові дроби: прихована краса.» Виконала: Учениця 9 «А» класу Бубнова Вікторія Керівник: вчитель математики Ярцева Ксенія Юріївна 2014-2015 навчальний рік

Ніщо не подобається, крім краси, у красі – ніщо, крім форм, у формах – ніщо, крім пропорцій, у пропорціях – ніщо, крім числа. Аврелій Августин, християнський теолог та філософ

МУНІЦИПАЛЬНА БЮДЖЕТНА ОСВІТАЛЬНА УСТАНОВА «Середня школа №15» м. Заволжжя Дослідницький проект з математики «Ланцюгові дроби: прихована краса.» Виконала: учениця 9 «А» класу Бубнова Вікторія Керівник: вчитель математики Ярцева Ксенія Юріївна 2014-2015 навчальний рік

Актуальність проекту Обчисліть значення виразу: .

Мета проекту - вивчення математичного об'єкта «ланцюговий дріб», його властивостей та методів вирішення завдань на цю тему. Завдання проекту Вивчити історію виникнення ланцюгових дробів; Дослідити властивості ланцюгових дробів та можливі дії, що виробляються з ними; Вивчити способи вирішення завдань із даними дробами; Вивчити алгоритмічну структуру, що працює за принципом ланцюгового дробу; З'ясувати можливість геометричного зображення ланцюгових дробів; З'ясувати можливість застосування ланцюгових дробів у інших науках.

Історична довідка Рафаель Бомбеллі італійський математик (1526-1572) Християн Гюйгенс нідерландський механік, фізик, математик, астроном та винахідник (1629-1695) Леонард Ейлер швейцарський, німецький та російський математик та механік7

Визначення Ланцюговий дріб (або безперервний дріб) - це математичний вираз виду

1 0 . Будь-яке раціональне число (де р > q) можна у вигляді кінцевого ланцюгового дробу Ірраціональні числа розкладаються в нескінченні ланцюгові дроби. Властивості

Властивості 2 0 . Обриваючи ланцюговий дріб, можна отримати дуже хороші раціональні наближення до даному числу, Які називаються відповідними дробами. Придатний дріб – це дріб, який виходить при обриві нескінченного ланцюгового дробу. Для числа π = Перші відповідні дроби – це найвідоміші наближення:

Реалізація алгоритму переведення ланцюгового дробу в дійсне число Програма запитує у користувача знаменник b і кількість вкладень n ланцюгового дробу виду перетворює її на число і видає результат у вигляді десяткового дробу.

Реалізація алгоритму переведення ланцюгового дробу до дійсного числа Program TO_NUMBER; var n, k: integer; b:real; begin write ("введіть знаменник дробу"); read (b); write ("введіть кількість вкладень"); read(n); для k:=1 до n до b:=1+1/b; write (" шукане число = ", b); end. Результати роботи програми Ланцюговий дріб перетворений на десятковий. Помилок не спостерігається. + Програма працює коректно. – Результат представлений у вигляді десяткового дробу. У разі її нескінченності комп'ютер округлює результат.

Реалізація алгоритму розкладання дійсного числа в ланцюговий дріб Програма просить користувача ввести число у вигляді десяткового дробу. Перетворивши його, видає результат виду Program TO_FRACTION; var a: array of integer; k, n: integer; x:real; begin write ("введіть число"); read(x); k:=1; a:=trunc(x); k:=2; while frac(x)0 do begin x:=1/ frac(x); a[k]:= trunc (x); k:=k+1; end; n:=k; write ("необхідне число x = ["); for k:=1 to n do write (a[k],","); write ("]"); end.

Результати роботи програми 1.8 = 1.6 = 1.65 = 7.3 помилка 101 – вихід за межі розмірності масиву 2.5 = 4.75 = Опис помилок У більшості випадків через заокруглення нескінченних періодичних десяткових дробів відбувається накопичення похибки. У деяких випадках зафіксовано некоректну роботу функції trun с(). У деяких випадках зафіксовано некоректну роботу функції frac (). Реалізація алгоритму розкладання дійсного числа в ланцюговий дріб

Рекурсивним називається спосіб побудови об'єкта (поняття, системи, опис дії), у якому визначення об'єкта включає аналогічні об'єкти (поняття, систему, дію) як складових частин. Алгоритмічна структура "Рекурсія"

Ланцюги та музика Йоганн Себастьян Бах клавір

Ланцюгові дроби та астрономія

Ланцюгові дроби та архітектура Золотий перетин- Гармонійна пропорція

Ланцюгові дроби в природі

Геометричне уявлення ланцюгового дробу

Бенуа Мандельброт – батько фракталів французький математик, професор математичних наук, почесний викладач Єльського Університету, науковий співробітник компанії IBM, Баттельський член Тихоокеанської Національної лабораторії. (1924 - 2010)

Фрактали у природі

Фрактали у комп'ютерній графіці

Мій перший фрактал

«Ланцюгові дроби: прихована краса.» Дякую за увагу!

Попередній перегляд:

Муніципальна бюджетна освітня установа

«Середня загальноосвітня школа №15» м.Заволжя

Городецького району Нижегородської області

Дослідницький проект

по математиці

«Ланцюгові дроби: прихована краса»

Виконала:

Бубнова Вікторія Валеріївна

учениця 9 «А» класу

e-mail: [email protected]

Керівник:

вчитель математики та інформатики

Ярцева Ксенія Юріївна

e-mail: [email protected]

Адреса ОУ:

606524, Нижегородська область, Городецький район,

м. Заволжя, вул. Пушкіна, б.4, МБОУ ЗОШ №15

E-mail: [email protected]

2014-2015 навчальний рік

Введення у проблему

Щороку в нашій школі проводяться олімпіади та конкурси з різних предметів, у тому числі з математики. В одній і цих олімпіад мені зустрілося завдання виду:

Обчисліть значення виразу.

В курсі шкільної програми ми не проходили дані дроби, і я вирішила досліджувати цей матеріал самостійно.

Мета моєї роботи– вивчення історії ланцюгових дробів та застосування їх при вирішенні завдань.

Завдання:

• Вивчити історію виникнення ланцюгових дробів;
• Дослідити властивості ланцюгових дробів та можливі дії, що виробляються з ними;
• Вивчити способи вирішення завдань із даними дробами;
• Знайти алгоритмічну структуру, що працює за принципом ланцюгового дробу;
• З'ясувати можливість геометричного зображення ланцюгових дробів;
• З'ясувати можливість застосування ланцюгових дробів у інших науках.

1. Історія появи та розвитку ланцюгових дробів

За збереженими джерелами, ми знаємо,що ланцюгові дроби використовувалися у Стародавній Греції, Китаї та Єгипті.Вперше ланцюгові дроби як такі з'являються у підручнику"Алгебра" італійського математикаРафаеля Бомбеллі (1526-1572), що вийшов 1572 р.

Наступний крок у розвитку теорії ланцюгових дробів було зробленоХристияном Гюйгенсом (1629-1695).Він будував модель сонячної системиза допомогою набору зубчастих коліс. За розрахунками виявилося, що відношення числа зубців двох будь-яких коліс має бути рівним відношенню часів обертання двох планет навколо Сонця. Це ставлення виявляється досить точно як дробу з великим чисельником і великим знаменником. Виготовлення таких зубчастих коліс, практично дуже складно. Гюйгенс вирішив це завдання за допомогою розкладання звичайного дробу в ланцюговий дріб.

Можна сказати, що першим, хто систематизував знання про ланцюгові дроби і виклав повну їхню теорію, бувЛеонард Ейлер (1707–1783).Він опублікував свою першу роботу в 1744 р., в якій розглядав ланцюговий дріб загального виду. Слід зазначити, що сам термін «ланцюговий дріб» виник лише у XVIII столітті, а до цього часу використовувалося поняття «безперервний дріб».

1. Властивості ланцюгових дробів

1 0 . Будь-яке раціональне число(де р>q) можна у вигляді кінцевоїланцюгового дробу

Числа, що входять до ланцюгового дробу, називаютьсянеповними приватними, їх a 1 , …, a n - натуральні, a 0 - ціле. Ірраціональні числа розкладаються в нескінченні ланцюгові дроби.

приклад.

2 0 . Обриваючи ланцюговий дріб, можна отримувати дуже хороші раціональні наближення до цього числа, які називаютьсявідповідними дробами.

Придатний дріб– це дріб, який утворюється при обриві нескінченного ланцюгового дробу.

Для числа π = з давніх часів відомі наближеннята .

Мною було прийнято рішення написати програми мовою програмування Pascal для перекладу ланцюгового дробу у дійсне число та назад.

Програма обчислення значення ланцюгового дробу

Програма просить користувача ввести чисельник дробу та кількість вкладень ланцюгового дробу. Перетворює її на число і видає результат у вигляді десяткового дробу.

Program TO_NUMBER;

var n, k: integer;

B:real;

begin

write ("введіть знаменник дробу"); read (b);

write ("введіть кількість вкладень"); read(n);

для k:=1 до n до b:=1+1/b;

Результати роботи програми

Ланцюговий дріб перетворений на десятковий. Помилок не спостерігається.

Висновок.

Програма працює коректно.

Результат представлений у вигляді десяткового дробу. У разі її нескінченності комп'ютер округлює результат.

Програма, що виконує розкладання числа в ланцюговий дріб

Програма просить користувача ввести число у вигляді десяткового дробу. Перетворивши його, видає результат виду

Program TO_FRACTION;

var a: array of integer;

K, n: integer;

X:real;

begin

write ("введіть число"); read(x);

k:=1; a:=trunc(x); k:=2;

while frac(x)0 do

begin

X:=1/frac(x);

A[k]:=trunc(x) ;

K:=k+1;

end;

n:=k;

write ("необхідне число x = [");

for k:=1 to n do write (a[k],",");

write ("]"); end.

Результати роботи програми

1.8 =

1.6 =

1.65 =

7.3 помилка 101 - Вихід за межі розмірності масиву

2.5 =

4.75 =

Опис помилок

1. Найчастіше через округлення нескінченних періодичних десяткових дробів відбувається накопичення похибки. При ручному рахунку ці дроби записуються як звичайних і помилки немає.
2. trunk() . Ця функція відсікає дробову частину дійсного числа.
3. У деяких випадках зафіксовано некоректну роботу функції frac() . Ця функція обчислює дрібну частину дійсного числа. Для цілих чисел результат її роботи повинен дорівнювати 0, але відбувається помилка.

1. Ланцюгові дроби та програмування

Принцип ланцюгового дробу співзвучний поняттю рекурсії у програмуванні.

Рекурсивним називається спосіб побудови об'єкта (поняття, системи, опис дії), у якому визначення об'єкта включає аналогічні об'єкти (поняття, систему, дію) як складових частин.

Приклади рекурсії можна зустріти у літературі, мистецтві, фольклорі.

«У попа був собака, він його любив.

Вона з'їла шмат м'яса, він її вбив.

Каменем придавив, і на камені написав:

«У попа був собака...»(Дитяча лічилка)

«Я озирнувся подивитися, чи не озирнулася вона,

щоб подивитися, чи не озирнувся я...»

(Максим Леонідов, "Дівчинка-бачення", пісня).

Зазвичай у програмуванні під рекурсією розуміють таку реалізацію, в якій підпрограма використовує у своєму тілі виклик самої себе.

Написані програмою використовували циклічний алгоритм.

Виправимо програму, використовуючи рекурсивний виклик функції num(a,m) яка обчислює значення одного вкладення ланцюгового дробу. Завдяки рекурсивності ми піднімаємося до першого вкладення ланцюгового дробу та отримуємо відповідь.

Program TO_NUMBER;

var n, k: integer;

B:real;

function num (a:real; m:integer):real;

Begin

If m=1 then num:=1+1/a

Else num:=1+1/num(a,m-1);

End;

begin

write ("введіть знаменник ланцюгового дробу"); read (b);

write (" введіть кількість вкладень ланцюгового дробу ");

read(n);

b:=num(b,n);

write (" шукане число = ", b); end.

1. Використання ланцюгових дробів у інших науках

Ланцюгові дроби - абстрактний об'єкт теорії чисел, вони широко використовуються в різних розділах математики та фізики, особливо в механіці. Але мене здивувало те, що вони дуже затребувані іншими науками.

З часів Баха у музиці використовується рівномірно темперована шкала, що містить 12 півтонів у кожній октаві. Чому ж виник розподіл октави саме на 12 інтервалів? Щоб октава і натуральна квінта по можливості більш точно укладалися в одну і ту ж рівномірну темперацію (розподіл октави на рівні по слуху інтервали), октаву потрібно поділити на стільки частин, щоб число log 2 (3/2) добре наближалося дробом з вибраним знаменником.

При розробці сонячного календарянеобхідно знайти раціональне наближення для числа днів на рік, яке дорівнює 365,2421988… Підрахуємо придатні дроби для дробової частини цьогочисла:

Перший дріб означає, що раз на 4 роки треба додавати зайвий день; цей принцип ліг основою юліанського календаря. При цьому помилка на 1 день накопичується за 128 років. Друге значення (7/29) ніколи не використовувалося. Третій дріб (8/33), тобто 8 ), помилка на добу накопичується лише за 100000 років) пропагував німецький астрономЙоганн фон Медлер (), проте великого інтересу не викликав.

Голландський учений Християн Гюйгенс в 1862 побудував один з перших механічних планетаріїв. Теорію ланцюгових дробів він застосувавпри проектуванні зубчастих колісщо забезпечило високу точність у взаємному русі моделей планет.

За допомогою теорії ланцюгових дробів обчислюється наближене значеннязолотого перетину. Це число відображає пропорції об'єктів, що сприймаються людиною як гармонійні. Правил золотого перерізу користуються архітектори, художники, дизайнери. Золотий перетин часто зустрічається в природі та повсякденному житті, навіть пропорції тіла людини близькі до цього числа.

Ще Гете наголошував на тенденції природи до спіральності. Гвинтоподібне та спіралеподібне розташування листя на гілках дерев помітили давно. Спіраль побачили у розташуванні насіння соняшника, у шишках сосни, ананасах, кактусах тощо. Спільна робота ботаніків та математиків пролила світло на ці дивовижні явища природи. З'ясувалося, що в розташуванні листя на гілці (філотаксис), насіння соняшника, шишок сосни виявляє себе ряд Фібоначчі, а отже, виявляє себе закон золотого перетину. Сама природа відбиває ланцюгові дроби, тільки це треба побачити. Це вкотре підтверджує афоризм Галілео Галілея:«Математика - це мова, якою написана книга природи».

1. Геометричне зображення ланцюгових дробів

Отже, ми зібрали безліч доказів про затребуваність ланцюгових дробів у різних науках. Більшість математичних об'єктів є геометрична інтерпретація. Спробуємо знайти її і для ланцюгових дробів.

Ми встановили зв'язок ланцюгових дробів та поняття рекурсії. Функція називаєтьсярекурсивний якщо вона містить одне або кілька звернень до самої себе. Рекурсії можна використовувати для отримання різноманітних привабливих картинок. Фігури з рекурсивною подобою називаютьсяфракталами . Збільшені деталі фракталу подібні до повного зображення.

Гіпотеза : Фрактал є графічним відображенням ланцюгового дробу

Фрактал (Від латинського «fractus» - розбитий, подрібнений, зламаний)- являє собою складну геометричну фігуру, яка складена з декількох нескінченної послідовності частин, кожна з яких подібна до всієї фігури цілком, і повторюється при зменшенні масштабу.

Дані математичні форми належать генію видатного вченогоБенуа Мандельброта. Своє відкриття він опублікував у наукових працях, присвячені вивченню "фрактальної геометрії" або "геометрії природи", в яких розбивав на перший погляд випадкові математичні форми на складові елементи, що опинилися при найближчому розгляді, що повторюються.

У природі фрактальними властивостями володіють багато об'єктів: крони дерев, цвітна капуста, хмари, кровоносна та альвеолярна системи людини та тварин, кристали, сніжинки, елементи яких вишиковуються в одну складну структуру, узбережжя (фрактальна концепція дозволила вченим виміряти берегову лініюБританських островів та інші, раніше незмірні, об'єкти).

Фрактальна геометрія внесла неоціненний внесок у розробку нових технологій у галузі цифрової музики, а також уможливила стиснення цифрових зображень. Фрактали широко застосовуються в комп'ютерній графіці – при побудові зображень дерев, поверхні морів, гірських ландшафтів та інших природних об'єктів. Цікаво, що окрім фрактального «живопису» існують так само фрактальна музика та фрактальна анімація. Фрактал побудований за математичною формулою не менш гарний, ніж природний.

З усіх геометричних об'єктів тільки фрактали мають властивості, подібні до властивостей ланцюгових дробів. На жаль, явного підтвердження своєї гіпотези в літературі я поки що не знайшла.

Висновок

У процесі роботи над проектом я вивчила багато літератури про ланцюгові дроби, навчилася використовувати їх при обчисленнях. Також зміцнила та розширила свої знання у програмуванні мовою Pascal.

Виникнувши із проблеми вирішення обчислювального завдання, проект переріс у цікаве дослідження. Я переконалася, що математика справді найкрасивіша з наук. Моя робота надихнула мене на створення фракталу. Ось що в мене вийшло.

Було б цікаво спробувати збудувати фрактал за допомогою комп'ютерних програм. Так залишилося відкритим питання про зв'язок фракталів та ланцюгових дробів. Якщо вона все-таки є, хотілося б навчитися по ланцюговому дробу будувати фрактал і описувати ланцюговим дробом вже готове зображення.

Список літератури

1. Хінчін А.Я. . Ланцюгові дроби. М.: Наука - 1978 - 112 с. з ілл.
2. Бескін Н. М.. Чудові дроби. Мінськ: Видавництво «Вища школа» – 1980 – 124 с.
3. Арнольд В. І. Ланцюгові дроби -М: Вид-во МЦНМО, 2009. - 40 с.
4. Журнал "Квант". Бескін М. Ланцюгові дроби (№1, 1970)
5. Журнал "Квант". Бескін М. Нескінченні ланцюгові дроби (N8, 1970)
6. Журнал "Квант". Бескін М. Нестеренко Ю., Нікішин Е. Нарис про ланцюгові дроби (N5,6, 1983)
7. Мандельброт Б.Б. Фрактальна геометрія природи: Пров. з англ. - М.: Ін-т комп'ютерних досліджень, 2002. - 656 с.

Вступ
	Історія розвитку ланцюгових дробів та їх застосування
		Історія появи та розвитку ланцюгових дробів
		Застосування ланцюгових дробів у теорії чисел
		Застосування ланцюгових дробів у аналітичній теорії
		Додатки ланцюгових дробів
	Наближення дійсних чисел раціональними дробами
		Подання дійсних чисел правильними ланцюговими дробами
			Розкладання дійсного числа у правильний нескінченний ланцюговий дріб
			Згортання ланцюгового дробу у звичайний дріб
		Наближення дійсних чисел відповідними дробами
			Властивості відповідних дробів
			Оцінка похибки під час заміни дійсного числа раціональним дробом
			Доказ теореми Діріхле про діофантові наближення
	Відповідні дроби як найкращі наближення
		Порівняння точності наближення відповідним дробом і будь-яким відповідним раціональним числом
		Ланцюгові дроби як апарат пошуку кращих наближень до заданого дійсного числа
		Алгоритм виділення найкращих наближень до заданого числа з множини раціональних чисел
Висновок
Література
Додаток 1

Вступ

В обчислювальній практицідійсні числа замінюють раціональними, при цьому раціональне число вибирають максимально простим у вигляді десяткового дробу з невеликим числом знаків після коми або звичайного з невеликим знаменником. У питаннях наближеного уявлення дійсних чисел раціональними дробами велике значеннямає апарат безперервних (ланцюгових) дробів.

Нескінченним ланцюговим, або безперервним, дробом загального виду називають розкладання

де можуть приймати довільні, відмінні від нуля раціональні значення, то, можливо одно нулю. Якщо в цьому дробі все , (), то дріб буде називатися правильним ланцюговим дробом.

Також розрізняють ланцюгові дроби, що гілкуються:

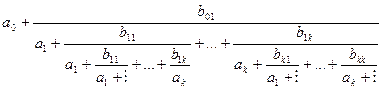
Дроби такого виду широко застосовують у багатьох питаннях обчислювальної математики.

У основі питання теорії ланцюгових дробів доступні учням основний школи. Її алгоритми ґрунтуються на застосуванні алгоритму Евкліда, виділення цілої частини числа. Її завдання пов'язані з апроксимацією дійсних чисел і спираються на теорію раціональних та дійсних чисел.

Мета даної роботи – вивчити ланцюгові дроби загального виду, розглянути можливі способи апроксимації дійсних чисел раціональними дробами та вибрати оптимальний, що дає найкращі наближення.

1. розглянути питання історії щодо появи та розвитку ланцюгових дробів, а також їх додатків;

2. опанувати алгоритми знаходження відповідних дробів для дійсних чисел;

3. вивчити основні властивості відповідних дробів ланцюгового дробу;

4. розглянути різні способи оцінки похибки, що виникають при апроксимації дійсних чисел раціональними дробами;

5. вибрати найкращі способиапроксимації дійсних чисел;

6. підібрати приклади для ілюстрації теоретичних положень.

Етапи дослідження:

1. 2003-2004 Курсова робота: «Наближення дійсних чисел ланцюговими (безперервними) дробами»

2. 2004-2005 Курсова робота: «Систематичні ланцюгові дроби як апарат подання дійсних чисел у школі»

3. 2005-2006 Випускна кваліфікаційна робота «Апроксимація дійсних чисел раціональними дробами».

Дослідну перевірку розробленого факультативу було проведено у 8-му класі ліцею ім. М.В.Ломоносова м. Йошкар-Ола у 2004-2005 навчальному році. Цей курс підтвердили інтерес учнів до цієї теми, гарне засвоєння теорії та успішність її застосування до вирішення завдань. За результатами апробації було опубліковано статтю «Вивчення ланцюгових дробів на факультативних заняттях з математики». Результати досліджень доповідалися на науковій студентській конференції 2005, 2006 року.

Робота складається з вступу, трьох розділів та висновків. Перший розділ містить питання історії появи та розвитку ланцюгових дробів, у ній також розглядається застосування безперервних дробів у теорії чисел та аналітичної теорії, а також їх застосування в інших галузях науки. До другого розділу включені елементи теорії ланцюгових дробів: уявлення дійсних чисел правильними ланцюговими дробами, наближення дійсних чисел відповідними дробами, оцінка похибки при заміні дійсного числа раціональним дробом. У третій главі показується, що відповідні дроби є найкращими наближеннями дійсного числа.

1. Історія розвитку ланцюгових дробів та їх застосування

1.1 Історія появи та розвитку ланцюгових дробів

За деякими даними, ланцюгові дроби застосовувалися вже математиками. Стародавню Грецію. Наприклад, алгоритм Евкліда (III в. е.) тісно пов'язані з ланцюговими дробами. Можливо, що при знаходженні наближення до Архімед (бл. 287-212 до н.е.) користувався методом, близьким до розкладання в ланцюговий дріб.

В 1858 був знайдений в курортному містечку на Нілі стародавній папірус, його називають також Папірус Ахмеса на ім'я писаря, що переписав його в 1650 до н. е. Якщо Архімед жив у III столітті до нашої ери, то папірус Рінда належить як мінімум до XVII; адже Ахмес був лише переписувачем, а автор (або, швидше, автори цієї праці) невідомий, але жив ще раніше. У папірусі Рінда міститься дивовижна формула для обчислення площі кола: 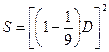, де S-площа, а D – діаметр кола. Формула дана у вигляді рецепта: «Візьми діаметр кола і відкинь його дев'яту частку; на будівництві квадрат». Тут використовуються найкращі раціональні наближення. Важко сказати, однак, як єгиптяни знайшли цей коефіцієнт. Його могли знайти і просто підбором - що абсолютно виключено у разі наближення, знайденого Архімедом.

Відомо, що китайський астроном Цзу Чун-чжі (V ст. н.е.) показав, що π укладено між 3,1415926 та 3,1415927. він вказав як раціональне наближення до π величину.

З середньовічних математиків близько підійшов до ланцюгових дробів Омар Хайям (бл. 1048-1122). Він поклав їх у основу своєї ідеї реформи календаря. Тривалість року за його наближеннями становила добу та становила похибку лише 19 секунд на рік.

Але вперше ланцюгові дроби як такі з'являються в "Алгебрі" італійського математика Рафаель Бомбеллі (1526-1572), що вийшов у 1572 р. у статті, написаній у той час, коли в Італії та Франції вперше з'явилися алгебраїчні поняття та позначення. Бомбеллі прийшов до ланцюгових дробів, вивчаючи вилучення квадратного кореняіз чисел. Першим відомим використанням безперервного дробу є наближений вираз для наступного виду. Це окремий випадокформули .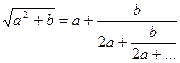

Наступне за часом застосування ланцюгового дробу, причому знову-таки до вилучення квадратних коренів належить італійському математику П'єтро Антоніо Катальді (1552-1626), їм було запропоновано другий окремий випадок цієї формули: 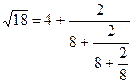. У 1613 р. він запровадив під час запису ланцюгового дробу повторне застосування дробової межі, тобто. вже справжнє позначення ланцюгового дробу, тільки замість він використовував перлюет (&), тобто. скорочене позначення латинського союзу et(і). І його запис розкладання виглядав так: =4&&… Крім розкладання ірраціонального числа в ряд Катальді ще й знайшов наближення цього числа: 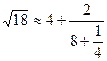і 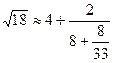, між якими укладено (хоча він не знав способу послідовного обчислення відповідних дробів). При цьому Катальді зауважив, що значення ланцюгового дробу завжди укладено між сусідніми дробами.

Катальді і Бомбеллі прийшли до ланцюгових дробів, виходячи з вилучення квадратного кореня з чисел, а Даніель Швентер (1585-1636), німецький математик, прийшов до ланцюгових дробів шляхом наближеного уявлення звичайних дробів з великими чисельниками та знаменниками. Він розкладав звичайний дріб у ланцюгову, використовуючи таблицю, за допомогою дуже цікавого способу. Таким чином, він знайшов рекурентні співвідношення для послідовного обчислення чисельників та знаменників відповідних дробів. Але при цьому Швентер розглядав лише правильні дроби– дроби, чисельники яких усі рівні одиниці, проте знаменники є натуральними числами.

У середині XVII століття англійський математик Джон Валліс (1616-1703) першим за часом розклав трансцендентне число у нескінченний твір: ..., а У. Броункер (1620-1686), перший президент Королівського товариства, близько 1659 без доказу опублікував розкладання його в ланцюговий дріб: .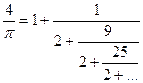

Наступний крок у розвитку теорії ланцюгових дробів було зроблено Християном Гюйгенсом (1629-1695). Він будував модель сонячної системи з допомогою набору зубчастих коліс. За розрахунками виявилося, що відношення числа зубців двох будь-яких коліс має бути рівним відношенню часів обігу двох планет навколо Сонця. Це відношення виражається досить точно у вигляді (нескоротного) дробу з великим чисельником та великим знаменником. Виготовлення таких зубчастих коліс, практично дуже складно. Тоді Гюйгенс знайшов серед дробів з меншим чисельником і меншим знаменником відповідний дріб до числа. Як і Швентер, Гюйгенс вирішив це завдання через розкладання звичайного дробу в ланцюговий дріб і тому обмежився розглядом правильних ланцюгових дробів. Завдяки чому було знайдено відповідний дріб, апроксимуючий дріб з великими чисельником і знаменником, і має похибку, яка становить лише десятитисячну частку від одиниці. Гюйгенс звернув увагу на те, що не можна знайти звичайний дріб з меншими чисельником і знаменником, ніж відповідний, який був би ближче до значення ланцюгового дробу; а також, що відповідні дроби поперемінно то більші, то менше значення ланцюгового дробу.

Можна сказати, що ланцюговими дробами займалися час від часу, і першим, хто систематизував знання про ланцюгові дроби і виклав повну їх теорію, наскільки це було можливо зробити в ту епоху, був Леонард Ейлер (1707-1783). Він опублікував свою першу роботу в 1744 р., в якій розглядав ланцюговий дріб загального виду та вперше з'являються відповідні ланцюгові дроби. Слід зазначити, що термін «ланцюговий дріб» виник лише у XVIII столітті, а до цього часу використовувалося поняття «безперервний дріб». Друга робота Ейлера, що вийшла в 1750 р., фактично була її продовженням, в ній розглядалися питання про застосування ланцюгових дробів для вирішення диференціальних рівнянь, алгоритм знаходження відповідних дробів, перетворення числових рядів у рівноцінні ланцюгові дроби, подання ірраціональних чисел на ланцюгові дроби деяких із них відповідних дробів. З його робіт стало ясно, що безперервні дроби можуть застосовуватися як теорії чисел, так і в аналізі. Ейлеру також належать і багато інших робіт, пов'язаних з вивченням та застосуванням ланцюгових дробів.

1.2 Застосування ланцюгових дробів у теорії чисел

Завданнями, що належать до теорії чисел, є розкладання дійсних чисел у правильні безперервні дроби та апроксимацію дійсних чисел за допомогою ланцюгових (безперервних) дробів. Тут найважливішим є питання щодо ступеня наближення, яке забезпечує n-я підходящадріб і оцінки похибки заміні дійсного числа відповідним дробом.

Великий внесок у теорію правильних безперервних дробів зробив Жозеф Луї Лагранж (1736-1813), який доказав, що квадратичні ірраціональності є саме ті числа, які мають періодичні розкладання (починаючи з деякого n). Їм запропоновано нерівність, що оцінює похибку при заміні дійсного числа його відповідним дробом, а також вирішення рівняння Пелля, де і - ірраціональне числоу вигляді пари { P n ( ), Q n ( )} для деяких значень n. Закінчене вирішення цього завдання дав Адрієн Марі Лежандр (1752-1833); приватні рішення були вже отримані Ейлером (рівняння Пелля цікаве, зокрема, тим, що може бути використане при розв'язанні задач адитивної теорії чисел, таких, як, наприклад: «Кожне просте число виду 4n+1 є сумою двох квадратів». – Такий результат сформулював П'єр Ферма (1601-1665) і вперше довів Ейлер, а доказ, заснований на безперервних дробах, дав Карл Фрідріх Гаус (1777-1855)).

Еваріст Галуа (1811-1832) у своїй першій опублікованій роботі досліджував деякі періодичні правильні безперервні дроби. Він дав визначення двоїстих періодичних правильних безперервних дробів.

Жозеф Ліувілль (1809-1882) першим довів існування трансцендентних чисел. У 1851 р. він зазначив, що алгебраїчні числа не можуть бути досить точно апроксимовані раціональними числами. Він довів, що для - кореня неприведеного полінома з цілими коефіцієнтами ступеня nіснує константа з: 0< c <1 , що всім відповідних дробів виконується нерівність . Використовуючи цей результат, він отримав можливість навести скільки завгодно багато прикладів трансцендентних чисел.

Результат, отриманий Адольф Гурвіцем (1859-1919) в 1891, полягає в тому, що нерівність завжди має нескінченну кількість раціональних рішень (Т. 12, С. 33). Еміль Борель (1871-1956) дав простий доказ цього факту, помітивши, що серед будь-яких трьох наступних одна за одною наступних дробів правильного безперервно-дрібного розкладання є хоча б одна, яка задовольняє цій нерівності.

Відтінок теорії міри надали цим результатам Борель і Фелікс Бернштейн (1878-1956), які довели, що для багатьох х: 0< x <1 , Послідовність ( a n) не обмежена. А.Я.Хинчин (1894-1959) дав розвиток цього напрямку – він заснував метричну теорію безперервних дробів .

1.3 Застосування ланцюгових дробів у аналітичній теорії

Значний внесок у аналітичну теорію зробив Ейлер. Їм були отримані розкладання в безперервні дроби для інтегралів і статечних рядів, включаючи і розбіжні, а також показав, як розкладання Броункера може бути виведено або з формули приведення Валліса, або з знакозмінного ряду Грегорі – Лейбніца для . Іншим внеском Ейлера було вирішення диференціального рівняння Ріккаті за допомогою безперервних дробів. В аналітичному напрямку теорії ланцюгових дробів працювали Йоган Генріх Ламберт (1728-1777) (розклав у безперервні дроби) ln (1+ x ), arctgxі tgx; і повністю досліджував питання збіжності безперервних дробів до цих функцій), Лагранж, Гаус, Карл Густав Якобі (1804-1851). Дев'ятнадцяте століття стало часом бурхливого розвитку аналітичної теорії ланцюгових дробів. Методи безперервних дробів використовувалися щодо спеціальних функцій, знаходження конкретних чисельних результатів. У галузі теорії розкладання та збіжності безперервних дробів, елементами яких є лінійні функції комплексного змінного, працювали такі математики, як П'єр Симон Лаплас, Лежандр, Якобі, Ейзенштейн, Лаггер, Бернхард Ріман (1826-1866), Томас Іоаннес Стілтьєс, П. Чебишев (1821-1894), Фробеніус (1849-1917) та Анрі Пуанкаре (1854-1912). Ці дослідження вплинули на подальший розвиток математики. Особливо це відноситься до робіт Стілтьєса, які привели до таких важливих досліджень, як проблема моментів, теорія інтеграла Стілтьєса, початок систематичного вивчення збіжності послідовностей голоморфних функцій та перше застосування Гільбертом та його школою апарату спектральної теорії самопов'язаних операторів у гільбертовому просторі до проблеми моментів. У роботах Пуанкаре і Стілтьєса, в яких розкладання в безперервні дроби застосовувалися у зв'язку з рядами, що розходяться, мабуть, вперше з'явилися асимптотичні розкладання.

Методи, розроблені Фробеніусом і Паде в кінці XIX століття для наближення аналітичних функцій відповідними дробами безперервних дробів під загальною назвою апроксимацій Паде, стали головним обчислювальним засобом у завданнях статистичної механіки та фізики твердого тіла, швидко поширюючись на інші розділи теоретичної фіз.

Гейне у 1846-1847 рр. займався гіпергеометричними функціями. Проблемою збіжності безперервних дробів відносин цих функцій – Ріман, і найповніше це питання було розглянуто Томе. Розв'язання завдання подання довільних статечних рядів ланцюговими дробами було розпочато Штерном у 1832 р. та Хейлерманом у 1846 та продовжено Фробеніусом та Стілтьєсом. Інтерес до цієї теми виявляли багато математиків, їхні роботи грали велику роль для науки. Нею також активно займалися і російські вчені: у ХІХ столітті роботи П.Л. Чебишева, А.А.Маркова (1856-1922), І.В.Слешинського та інших математиків зробили значний внесок у теорію ланцюгових дробів.

У Марійському педагогічному інституті під керівництвом А.Н.Хованського у 50-60-ті роки XX століття працювала аспірантура, в якій займалися дослідженням аналітичних питань ланцюгових дробів. Надалі успішно захистили кандидатські дисертації та опублікували низку робіт Г.В. Маурер, Л.П. Шутова, C.С. Хлопонін, В.К. Смишляєв.

Таким чином, завдяки систематичному вивченню Ейлером ланцюгових дробів, багато математиків, що працюють у Росії та за її межами, зацікавилися цим питанням і продовжили його вивчення у своїх роботах. Величезна кількість робіт, присвячених теорії ланцюгових дробів, говорить про широкі можливості застосування її до різних галузей науки.

1.4 Додатки ланцюгових дробів

Ланцюгові і розгалужені ланцюгові дроби мають ряд унікальних властивостей, що забезпечують їм широке використання в теоретичній та прикладній математиці. Цим пояснюється підвищений інтерес математиків до цієї теорії протягом кількох століть.

Застосування ланцюгових дробів під час вирішення класичної завдання давнини про побудову квадрата, рівновеликого даному колу (квадратура кола) зіграло свою роль при знаходженні значення числа π. Проблема складання календаря тісно пов'язана із ланцюговими дробами. Вперше порядок у часі спробував навести в I в. до. н.е. римський імператор Юлій Цезар, та його календар був мало точний. За юліанським календарем до XVI ст. накопичилася помилка, що становить близько 10 діб. Внаслідок чого була проведена наступна реформа календаря папою римським Григорієм XIII, ім'ям якого і називається діюча система календаря. Вирішенням цього завдання займалося багато математиків серед них і Омар Хайям, про його систему календаря було розказано раніше. У 1864 р. російським астрономом І. Медлером була запропонована ще одна поправка до юліанського календаря, заснована на знаходженні вже четвертого відповідного дробу до запису тривалості астрономічного року у вигляді ланцюгового дробу. Вирішенням ще однієї задачі XVII століття займався Х.Гюйгенс при побудові планетарію (С.8).

В даний час у теоретичному плані безперервні дроби відіграють істотну роль, оскільки дозволяють посилити і розвинути результати класичної математики на випадок багатьох аргументів, причому сам апарат ланцюгових дробів найчастіше нагадує формулювання таких узагальнень, зокрема, в теорії чисел.

Ланцюгові дроби широко застосовуються в теорії чисел: узагальнено деякі основні алгоритми (алгоритм Евкліда, Остроградського, Ейлера), знайдено рішення класичної задачі про ірраціональності алгебри вищих ступенів, знайдені окремі рішення деяких діофантових рівнянь та їх систем.

Ланцюгові дроби дають велику перевагу точно при наближеному знаходженні коренів квадратних рівнянь; обчисленні логарифмів чисел.

Ланцюгові дроби дозволяють будувати алгоритми для обчислення коренів рівнянь алгебри довільного ступеня. У обчислювальній практиці використовуються при вирішенні порівнянь першого ступеня, також зручні у використанні дрібно-раціональні апроксимації функцій одного аргументу ланцюговими дробами за допомогою формул Обрешкова або Тілі за методом Паде. Вони також застосовуються в теорії порівнянь.

На базі ланцюгових дробів побудовані деякі ефективні методи розв'язання алгебраїчних та трансцендентних рівнянь, невизначених рівнянь виду , рівнянь рекурентного типу та інших типів рівнянь. Розв'язання задачі Коші для лінійних систем диференціальних рівнянь з приватними похідними можна представити ланцюговими дробами, що гілкуються, при накладенні деяких умов до системи та початкових умов.

Ланцюгові дроби використовуються для знаходження наближених уявлень функцій. Ці наближення, що є дробно-раціональними функціями від незалежних змінних, успішно замінюють цю функцію в тих областях зміни аргументу, де, наприклад, розкладання цієї функції в статечний ряд розходиться і де, отже, наближення у вигляді багаточленів у більшості випадків непридатні. З використанням дробно-раціональних наближень відпадає необхідність обчислювати високі ступеня аргументу і з'являється можливість обчислювати значення окремих функцій.

Теорія матричних гілчастих ланцюгових дробів дозволяє вирішити наступні завдання: вилучення квадратного кореня, кореня третього, четвертого ступеня і кореня будь-якого раціонального ступеня за допомогою матриць, вирішення рівнянь за допомогою матриць другого порядку, вирішення рівнянь вищих ступенів за допомогою матриць. (Матричні рекурентні рівняння застосовують у завдання економіки, фізики, плазми та інших.) .

Нині ланцюгові дроби знаходять дедалі більше застосування обчислювальної техніки, оскільки дозволяють будувати ефективні алгоритми на вирішення низки завдань на ЕОМ.

Крім теоретичного використання правильних ланцюгових дробів існують і практичні застосування ланцюгових дробів. Серед усієї їх множини можна відзначити такі:

· Вирішення зворотних завдань теплопровідності;

· Дослідження механічних коливань у валопроводах різних енергетичних установок;

· Синтез пристроїв частотної селекції на функціональних часозадаючих елементах;

· Дослідження стійкості, дослідження встановлених і перехідних процесів, стабілізація систем, дослідження та забезпечення якості систем, дослідження випадкових процесів, оптимізація параметрів та ряд інших проблем у техніці, зокрема, в автоматиці, радіоелектроніці, приладобудуванні та ін.

Література

1. Боднарчук, П.І. Успіхи та завдання теорії ланцюгових і розгалужених ланцюгових дробів / П.І. Боднарчук, В.Я. Скоробогатько // Ланцюгові дроби їх застосування: Зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 5 – 8

2. Бухштаб, А.А. Теорія чисел/А.А. Бухштаб. - Вид. 2-ге, перероб. та дод. - М: Просвітництво, 1966. - 384 с.

3. Гапоненко, Н.П. Ланцюгові дроби в синтезі пристроїв частотної селекції на функціональних елементах, що час задаються / Н.П.Гапоненко, Н.Н.Рябець // Ланцюгові дроби їх застосування: зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 48 – 49.

4. Глейзер, Г.І. Історія математики у середній школі. Посібник для вчителів/Г.І. Глейзер. - М: Просвітництво, 1970. - 461с., іл.

5. Джоунс, У. Безперервні дроби. Аналітична теорія та додатки / У. Джоунс, В. Трон; Переклад з англ. В. Є. Кондрашова, С. Б. Корольова та І. Г. Турундаєвської; за ред. І. Д. Софронова - М: Світ, 1985. - 416 с.

6. Зотов, Є.М. Розв'язання обернених завдань теплопровідності за допомогою ланцюгових дробів/Е.Н.Зотов, Н.П.Пучков, Ю.С. Шаталов // Ланцюгові дроби їх застосування: Зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 56 – 57.

7. Кудреватов, Г.А. Збірник завдань з теорії чисел/Г.А. Кудряватів. - М: Просвітництво, 1970. - с.

8. Ламберт, І.Г. Попередні відомості для тих, хто шукає квадратуру та спрямування кола. / І.Г. Ламберт// Про квадратуру кола: зб. наукових праць/під ред. акад. С.М.Бернштейна. - М.: Державне техніко-теоретичне видавництво, 1934. - С. 169-198

9. Математична енциклопедія: У 5 т. Т. 5: Ланцюгові дроби. - М.: Радянська енциклопедія, 1985.

10. Маурер, Г.В. Вирішення одного диференціального рівняння Ріккаті за допомогою ланцюгових дробів / Г.В. Маурер // Ланцюгові дроби їх застосування: Зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 76 – 77.

11. Маурер, Г.В. Про розкладання в ланцюгові дроби деяких граничних випадків функції Гейне. / Г.В. Маурер // Волзький математичний збірник: праці математичних кафедр педагогічних інститутів Поволжя / КДПІ - вип. 5. - Казань: Видавництво казанського університету, 1966. - С. 211-221.

12. Маурер, Г.В. Про рішення деяких діофантових рівнянь другого ступеня. / Г.В. Маурер // Друга Всеросійська школа-колоквіум за стохастичними методами: тези доповідей. - М.: ТВП, 1995.

13. Маурер, Г.В. Вирішення деяких невизначених рівнянь другого ступеня за допомогою ланцюгових дробів загального виду / Г.В. Маурер / / Вчені записки МДПІ ім. Н.К.Крупської: Т. 26. - Йошкар-Ола, 1965. - С. 431-442.

14. Михелович, Ш.Х. Теорія чисел/Ш.Х. Михелович. - Вид. 2-ге, перероб. та дод. - М: Вища школа, 1967. - 336 с.

15. Нівен, А. Числа раціональні та ірраціональні / А. Нівен; переклад із англ. В.В. Сазонова; за ред. І.М. Яглома – М.: Світ, 1966. – 199с.

16. Пічурін, Л.Ф. За сторінками підручника алгебри: книга для учнів 7-9 класів порівн. школи/Л.Ф. Пічурін - М.: Просвітництво, 1990. - 237с.

17. Рудіо, Р. Огляд історії задачі про квадратур кола від давнини до наших днів. / Р. Рудіо // Про квадратур кола / за ред. акад. С.М.Бернштейна. - М.: Державне техніко-теоретичне видавництво, 1934. - С. 9-94

18. Семенова, О.Д. Вивчення ланцюгових дробів на факультативних заняттях з математики/ Є.Д. Семенова, О.Г. Кукліна // Педагогіка майбутнього: збірник наукових праць аспірантів та студентів. Вип. 2/під ред. Г.В. Рокіної. - Йошкар-Ола. - 2005. - С.305-308

19. Смишляєв, В.К. Збіжності стиснених ланцюгових дробів. Аналітична геометрія трикутника питання теорії ланцюгових дробів/В.К. Смишляєв // Вчені записки МДПІ ім. Н.К.Крупської: Т. 26. - Йошкар-Ола, 1965. -С.443-444

20. Терських, В.П. Ланцюгові дроби - математичні моделі ланцюгових систем, що вагаються / В.П. Терських // Ланцюгові дроби їх застосування: Зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 34 – 40.

21. Хінчін, А.Я. Ланцюгові дроби. / А Я. Хінчін - М.: ГІФ - МЛ, 1961, 112с.

22. Хлопонін, С.С. Області збіжності ланцюгових дробів/С.С. Хлопонін // Ланцюгові дроби їх застосування: Зб. наукових праць/під ред. В.Я. Скоробогатько. Інститут математики АН УРСР. – Київ, 1976. – С. 96 – 97.

23. Хлопонін, С.С. Збіжність ланцюгових дробів. / С.С. Хлопонін / / Волзький математичний збірник: праці математичних кафедр педагогічних інститутів Поволжя / КДПІ - вип. 5. - Казань: Видавництво казанського університету, 1966. - С. 354 – 362.

24. Хованський, А.М. Додаток ланцюгових дробів та їх узагальнень до питань наближеного аналізу/О.М. Хованський. - М: Державне видавництво техніко-теоретичної літератури, 1956. - 204 с.

25. Хованський, А.М. Роботи Л.Ейлера з теорії ланцюгових дробів/О.М. Хованський// Історико-математичні дослідження. - Вип. 10. - С.305-326.

26. Шутова, Л.П. Про одне узагальнення алгоритму ланцюгових дробів та його додаток до наближеного обчислення деяких функцій / Л.П. Шутова / / Волзький математичний збірник: праці математичних кафедр педагогічних інститутів Поволжя / КДПІ - вип. 5. - Казань: Видавництво казанського університету, 1966. - С.406 - 413.