Ступінь із раціональним показником, її властивості. Ступінь із ірраціональним показником. Показова функція. Ступінь із раціональним показником
Ступінь з раціональним показником, її властивості.
Вираз а n визначено для всіх а та n, крім випадку а=0 при n≤0. Нагадаємо властивості таких ступенів.
Для будь-яких чисел а, b та будь-яких цілих чисел m і п справедливі рівності:
A m *a n = a m+n; a m:а n = m-n (а≠0); (а m) n = а mn; (ab) n = n * b n ; (b≠0); а 1 = а; а 0 = 1 (а ≠ 0).
Відзначимо також таку властивість:
Якщо m>n, то m >а n при а>1 і а m<а n при 0<а<1.
У цьому пункті ми узагальним поняття ступеня числа, надавши сенс виразам типу 2 0.3 , 8
5/7 , 4
-1/2 і т. д. Природно при цьому дати визначення так, щоб ступеня з раціональними показниками мали ті ж властивості (або хоча б їх частиною), що й ступеня з цілим показником. Тоді, зокрема, n-й ступінь числаповинна дорівнювати а m . Справді, якщо властивість
(a p) q = a pq
виконується, то
Остання рівність означає (за визначенням кореня n-го ступеня), що числомає бути корінням п-го ступеня з числа а m.
Визначення.
Ступенем числа а>0 із раціональним показником r=, де m — ціле число, а n — натуральне (n > 1), називається число
Отже, за визначенням
(1)
Ступінь числа 0 визначено лише позитивних показників; за визначенням 0 r = 0 для будь-якого r>0.
Ступінь із ірраціональним показником.
Ірраціональне числоможна уявити у виглядімежі послідовності раціональних чисел
:
.
Нехай. Тоді існують ступеня з раціональним показником. Можна довести, що послідовність цих ступенів є схожою. Межа цієї послідовності називається ступенем з основою та ірраціональним показником: .
Зафіксуємо додатне числоа і поставимо у відповідність кожному числу. Тим самим одержимо числову функцію f(x) = a x , визначену на безлічі Q раціональних чисел і що має раніше перераховані властивості. При а=1 функція f(x) = a x постійна, тому що 1 x =1 для будь-якого раціонального х.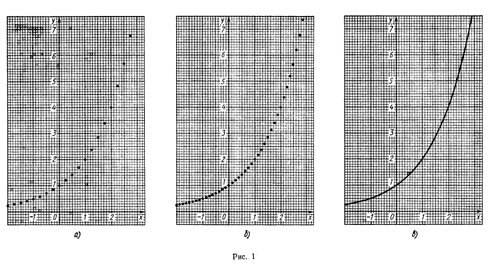
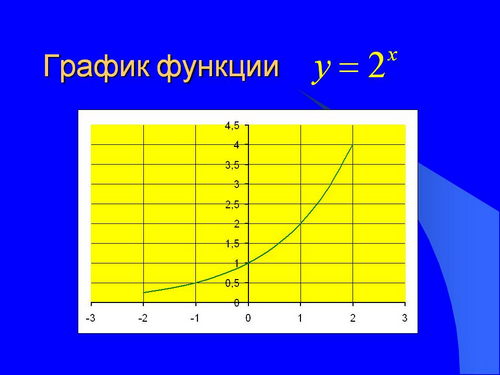
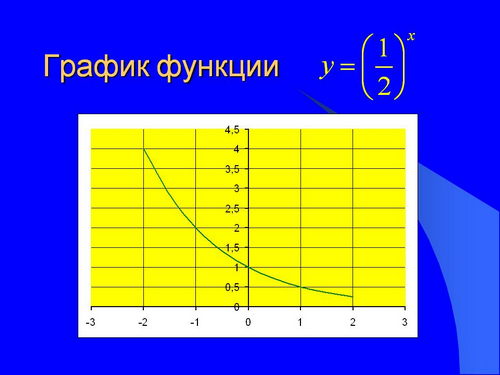
Нанесемо кілька точок графіка функції у = 2 x попередньо обчисливши за допомогою калькулятора значення 2 x на відрізку [-2; 3] з кроком 1/4 (рис. 1, а), а потім з кроком 1/8 (рис. 1, б). Продовжуючи подумки такі ж побудови з кроком 1/16, 1/32 і т.д. ми бачимо, що точки, що виходять, можна з'єднати плавною кривою, яку природно вважати графіком деякої функції, визначеної і зростаючої вже на всій числовій прямій і приймаючої значенняу раціональних точках(Рис. 1, в). Побудувавши досить велику кількість точок графіка функції, можна переконатися в тому, що аналогічні властивості має і ця функція (відмінність полягає в тому, що функціязменшується на R).
Ці спостереження підказують, що можна визначити числа 2α та для кожного ірраціонального α, що функції, що задаються формулами y=2 x і будуть безперервними, причому функція у = 2 x зростає, а функціяспадає на всій числовій прямій.
Опишемо загалом, як визначається число a α для ірраціональних α при а>1. Ми хочемо досягти того, щоб функція у = a x була зростаючою. Тоді за будь-яких раціональних r 1 і r 2 таких, що r 1<α
Вибираючи значення r 1 та r 2 , що наближаються до х, можна помітити, що відповідні значення a r 1 та a r 2 мало відрізнятимуться. Можна довести, що існує, і притому лише одне, число у, яке найбільше a r 1 для всіх раціональних r 1 і найменше a r 2 для всіх раціональних r 2 . Це число у визначенні є α .
Наприклад, обчисливши за допомогою калькулятора значення 2 x у точках хn і х`n, де хn і х`n - десяткові наближення числами виявимо, що, чим ближче х n і х`n до , тим менше 2 x n і 2 x`n.
Оскільки , то
![]() і, отже,
і, отже,
Аналогічно, розглядаючи такі десяткові наближенняза нестачею та надлишком, приходимо до співвідношень
;
;
;
;
.
Значення обчислене на калькуляторі, таке:
.
Аналогічно визначається число a α для 0<α<1. Кроме того полагают 1
α =1 для будь-якого α та 0α =0 для α>0.
Показова функція.
Ступінь із раціональним показником
Хасянова Т.Г.
викладач математики
Представлений матеріал буде корисний викладачам математики щодо теми «Ступінь з раціональним показником».
Мета представленого матеріалу: розкриття мого досвіду проведення заняття на тему «Ступінь з раціональним показником» робочої програми дисципліни «Математика».
Методика проведення заняття відповідає його типу - урок вивчення та первинного закріплення нових знань. Було проведено актуалізацію опорних знань та умінь на базі раніше отриманого досвіду; первинне запам'ятовування, закріплення та застосування нових відомостей. Закріплення та застосування нового матеріалу проходило у вигляді вирішення апробованих мною завдань різної складності, що дають позитивний результат засвоєння теми.
На початку заняття мною було поставлено перед учнями такі мети: освітня, розвиваюча, виховна. На занятті мною застосовувалися різні методи діяльності: фронтальна, індивідуальна, парна, самостійна, тестова. Завдання були диференційовані і дозволяли виявляти, кожному етапі уроку, ступінь засвоєння знань. Обсяг та складність завдань відповідає віковим особливостям учнів. З мого досвіду – домашнє завдання, аналогічне завданням, вирішеним у навчальному кабінеті, дозволяє надійно закріпити отримані знання та вміння. Наприкінці уроку було проведено рефлексію та оцінено роботи окремих учнів.
Цілей було досягнуто. Учні вивчили поняття та властивості ступеня з раціональним показником, навчилися використовувати ці властивості під час вирішення практичних завдань. За самостійну роботу оцінки оголошуються наступного уроці.
Вважаю, що методика проведення занять з математики, що застосовується мною, може бути застосована викладачами математики.
Тема заняття: Ступінь з раціональним показником
Мета уроку:
Виявлення рівня оволодіння учнями комплексом знань та умінь та на його основі застосування певних рішень щодо вдосконалення навчального процесу.
Завдання уроку:
Навчальні:формувати нові знання в учнів основних понять, правил, законів на визначення ступеня з раціональним показником, уміння самостійно застосовувати знання у стандартних умовах, у змінених та нестандартних умовах;
розвиваючі:логічно мислити та реалізовувати творчі здібності;
що виховують:формувати інтерес до математики, поповнити лексичний запас новими термінами, отримати додаткову інформацію про світ. Виховувати терпіння, посидючість, здатність долати труднощі.
Організаційний момент
Актуалізація опорних знань
При множенні ступенів з однаковими основами показники складаються, а основа залишається такою:
Наприклад, 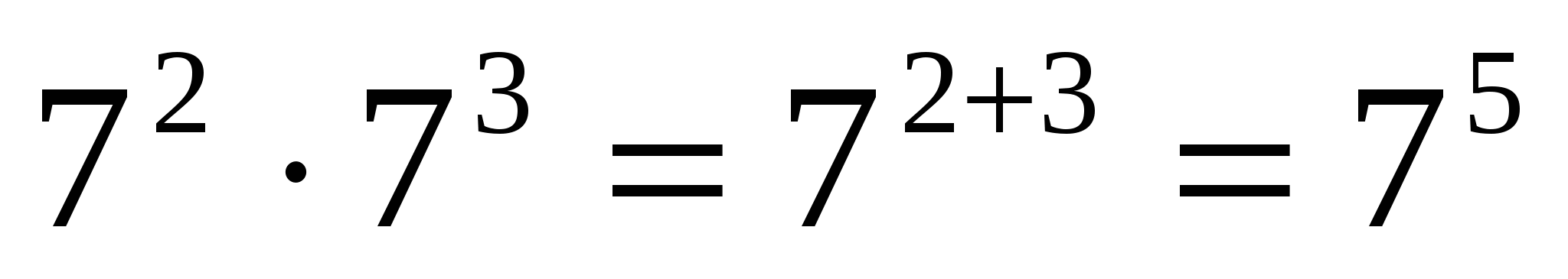
2. При розподілі ступенів з однаковими підставами показники ступенів віднімаються, а підстава залишається такою:
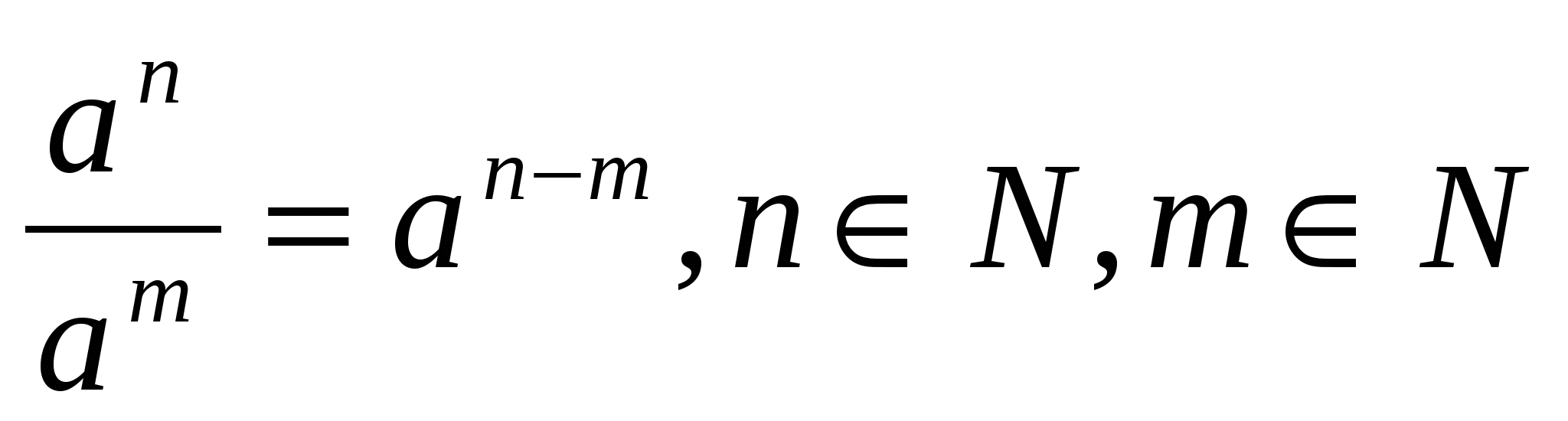 Наприклад,
Наприклад, 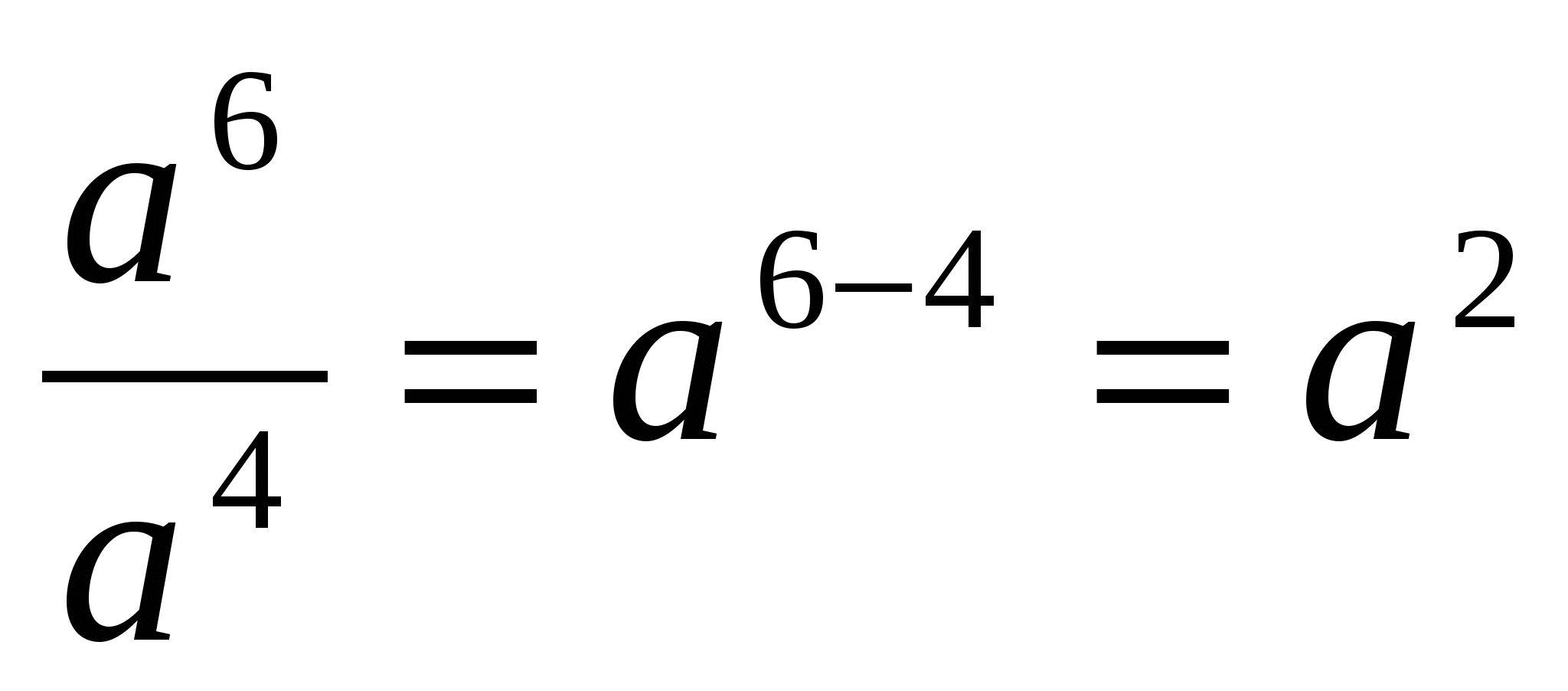
3. При зведенні ступеня в ступінь показники ступенів перемножуються, а підстава залишається такою:
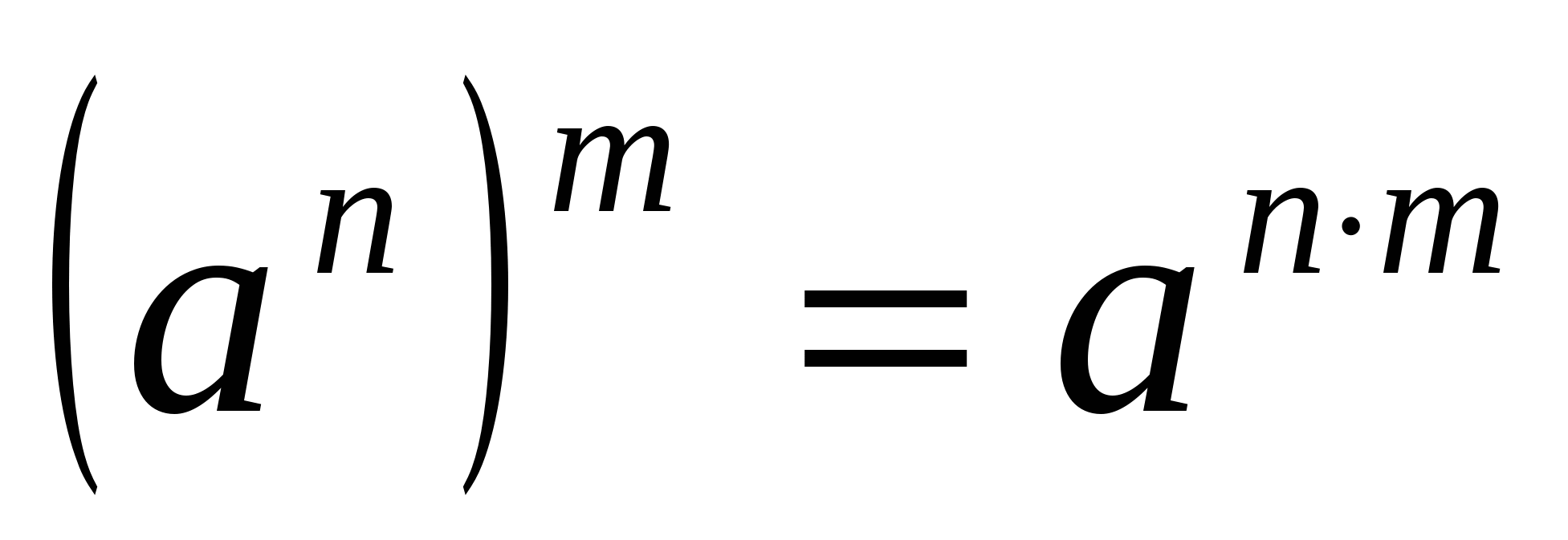 Наприклад,
Наприклад,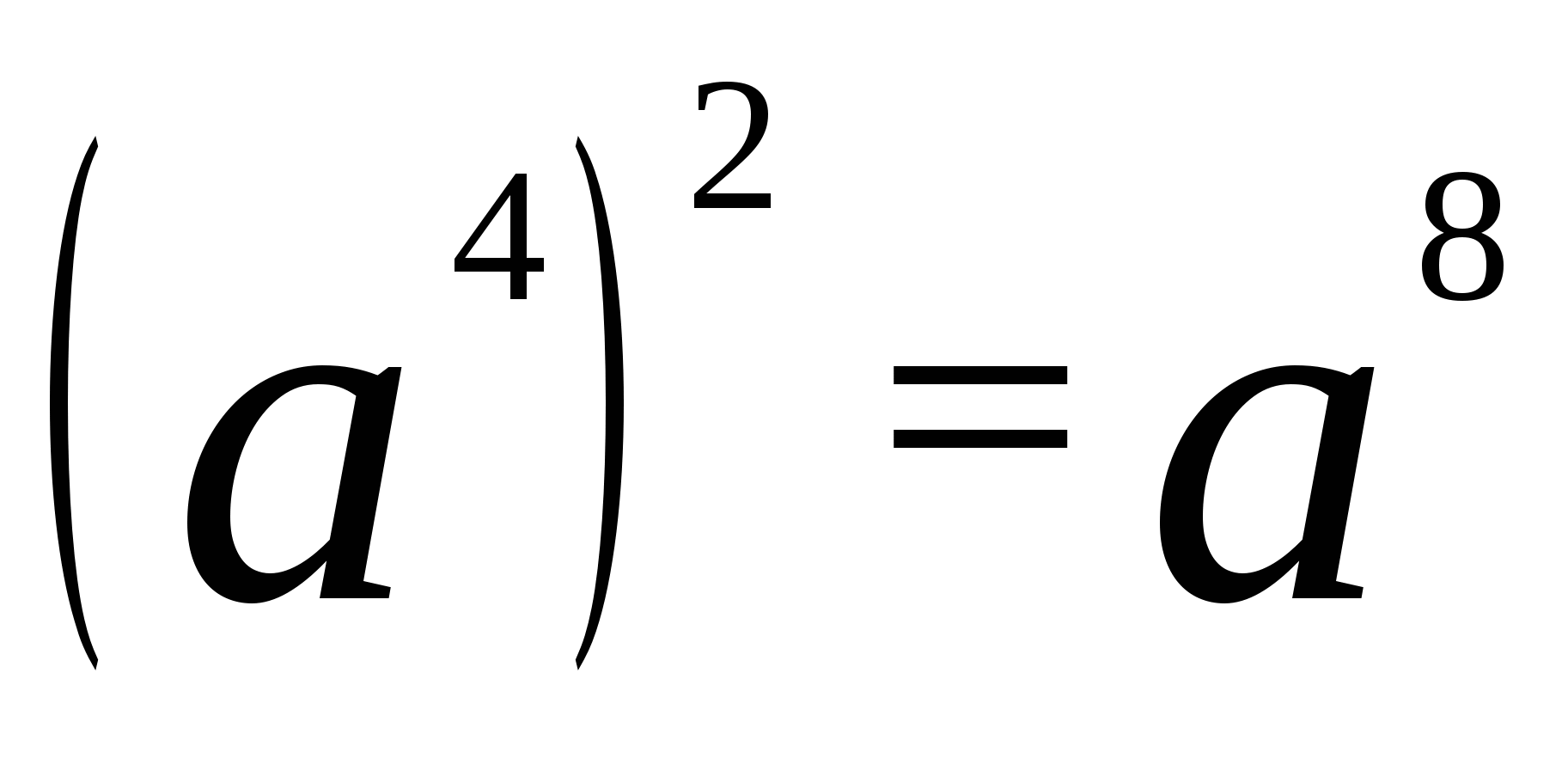
4. Ступінь твору дорівнює твору ступенів множників:
Наприклад, 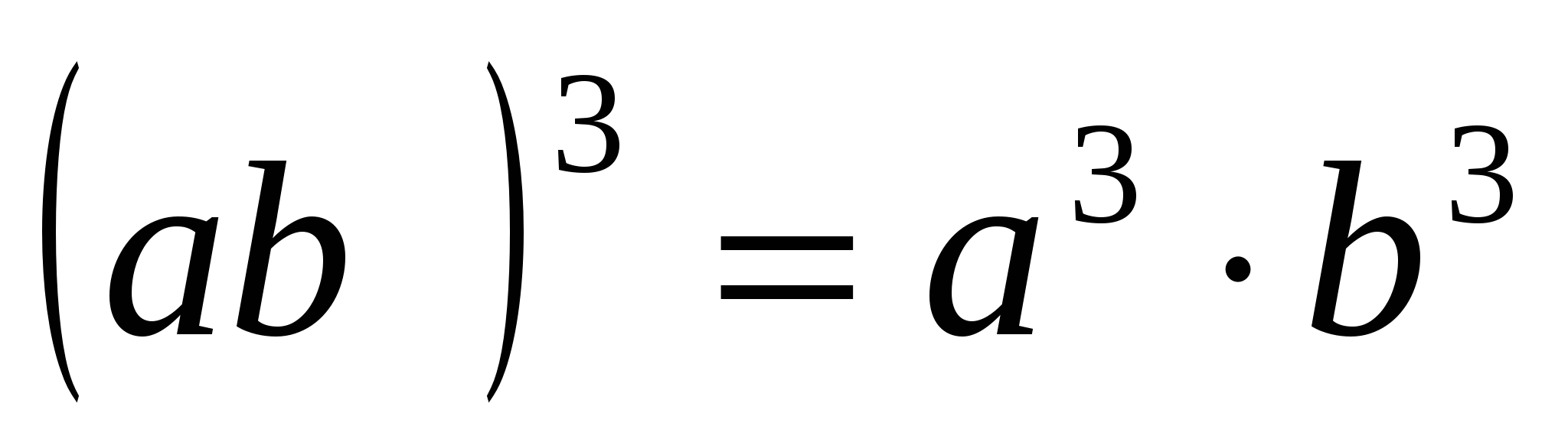
5. Ступінь приватного дорівнює приватному ступеню діленого н дільника:
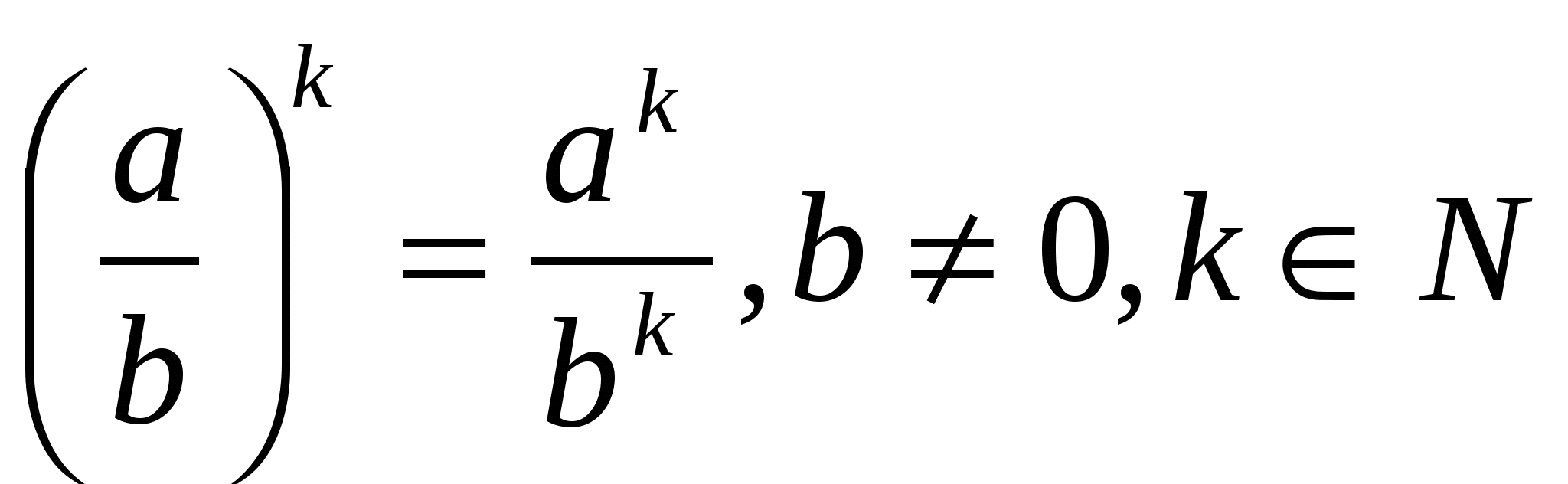 Наприклад,
Наприклад, 
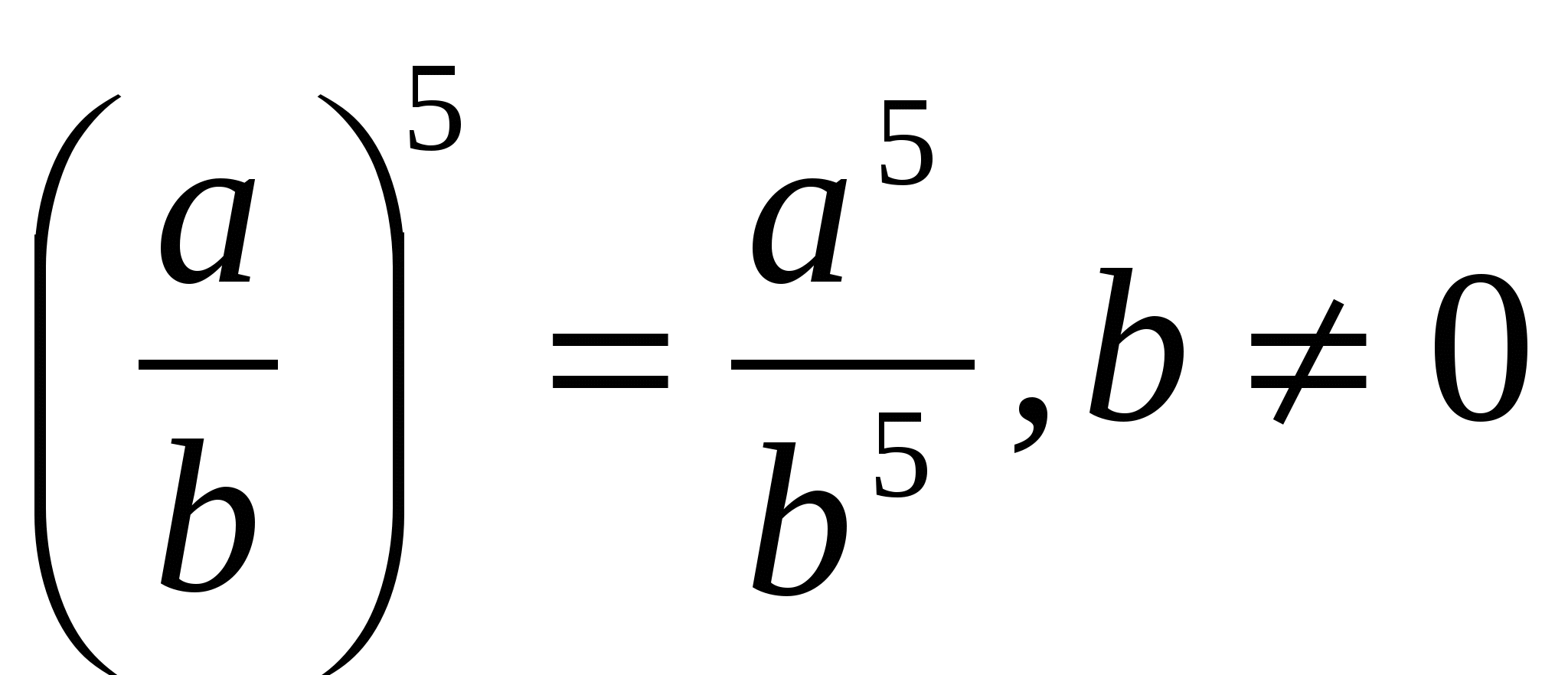
Вправи із рішеннями
Знайти значення виразу: 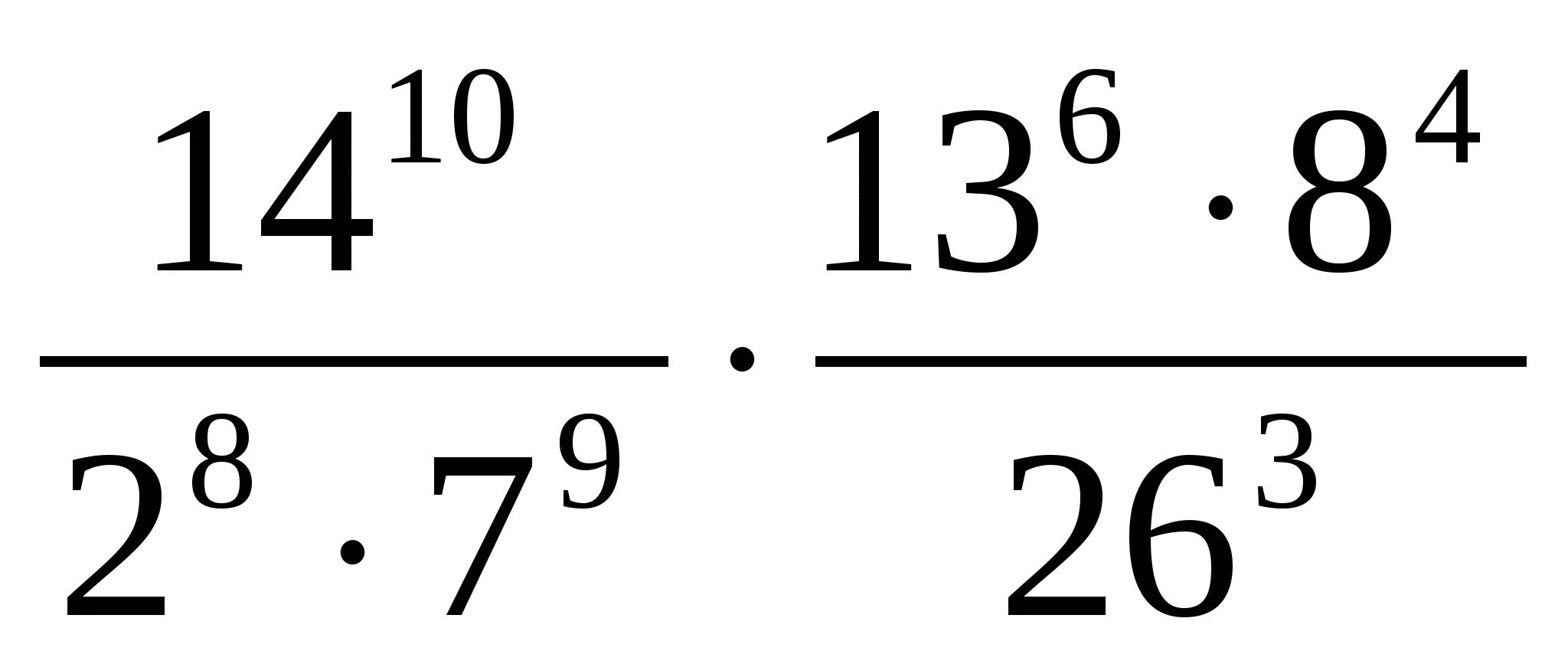
Рішення:
В даному випадку в явній формі жодна з властивостей ступеня з натуральним показником не можна застосувати, тому що всі ступеня мають різні підстави. Запишемо деякі ступені в іншому вигляді:
(ступінь добутку дорівнює добутку ступенів множників);
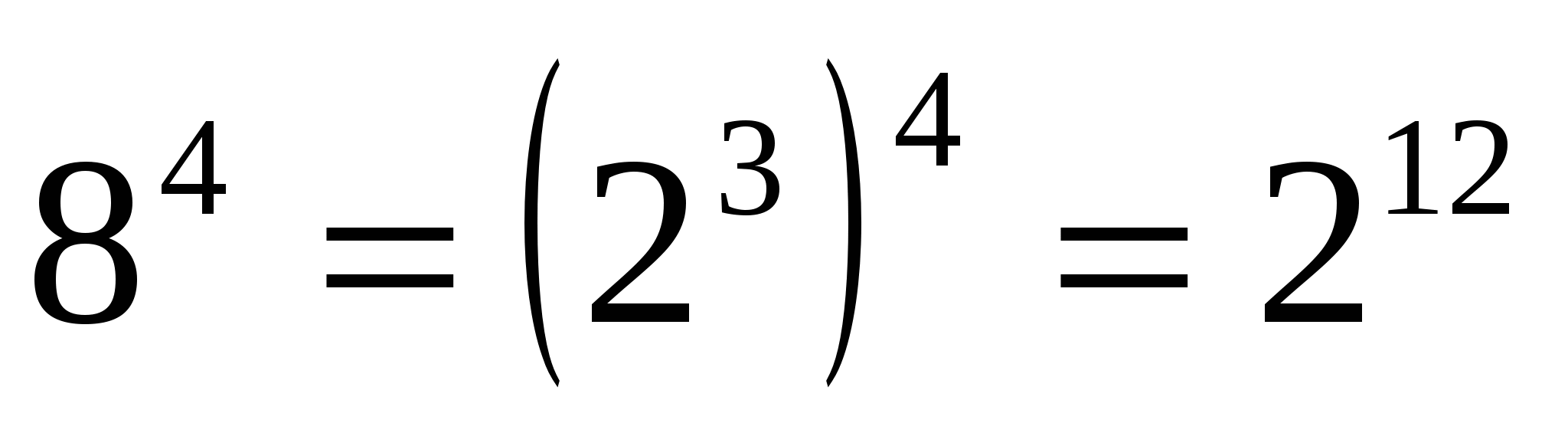 (при множенні ступенів з однаковими основами показники складаються, а основа залишається незмінною, при зведенні ступеня в ступінь показники степенів перемножуються, а основа залишається незмінною).
(при множенні ступенів з однаковими основами показники складаються, а основа залишається незмінною, при зведенні ступеня в ступінь показники степенів перемножуються, а основа залишається незмінною).
Тоді отримаємо:
У цьому прикладі були використані перші чотири властивості ступеня з натуральним показником.
Арифметичний квадратний корінь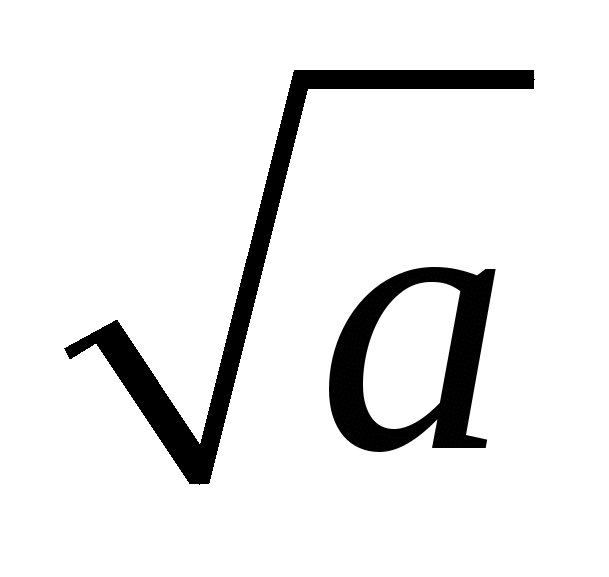 - це невід'ємне число, квадрат якого дорівнюєa,
- це невід'ємне число, квадрат якого дорівнюєa,
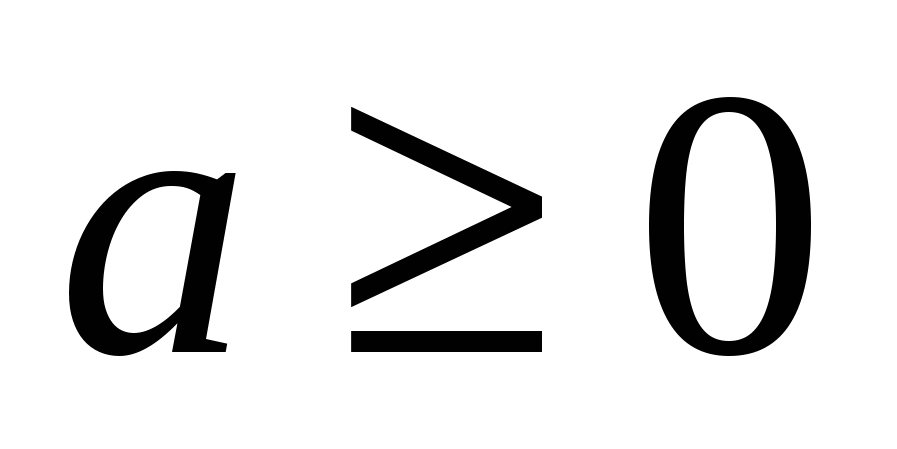 . При
. При 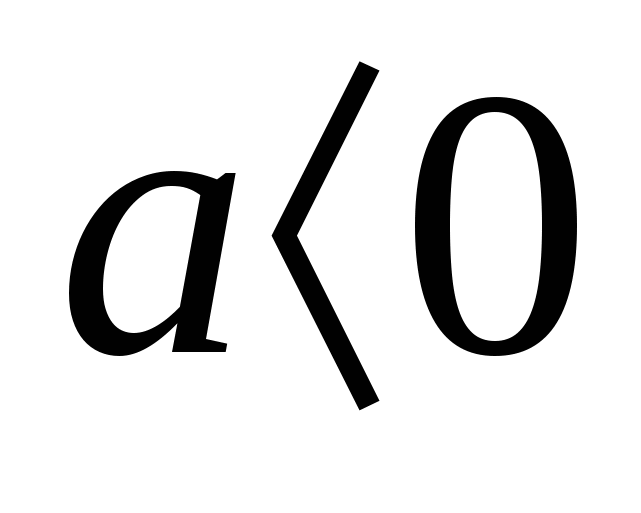 - Вираз
- Вираз 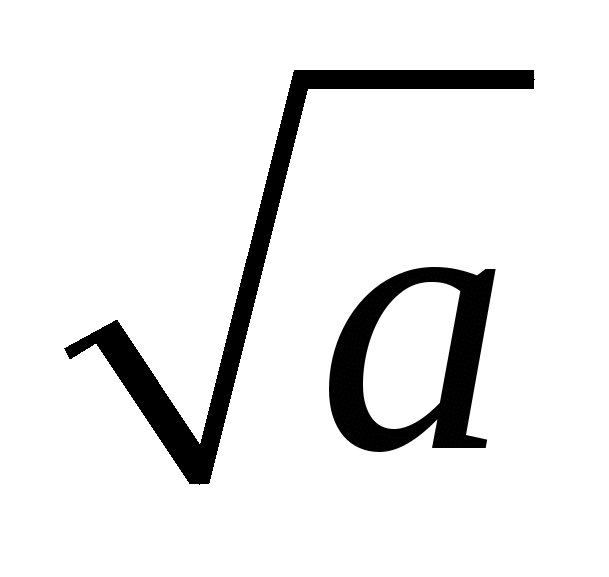 не визначено, т.к. немає такого дійсного числа, квадрат якого дорівнює негативному числуa.
не визначено, т.к. немає такого дійсного числа, квадрат якого дорівнює негативному числуa.
Математичний диктант(8-10 хв.)
варіант
ІІ. варіант
1.Знайти значення виразу
а) 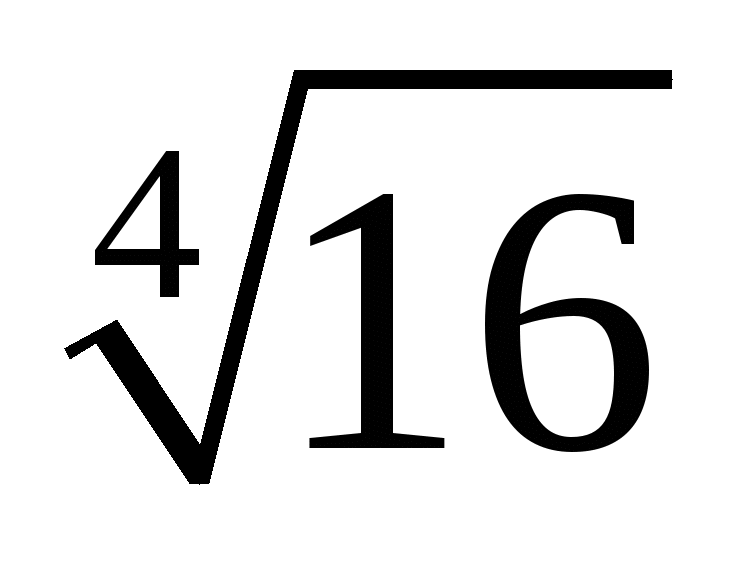
б) 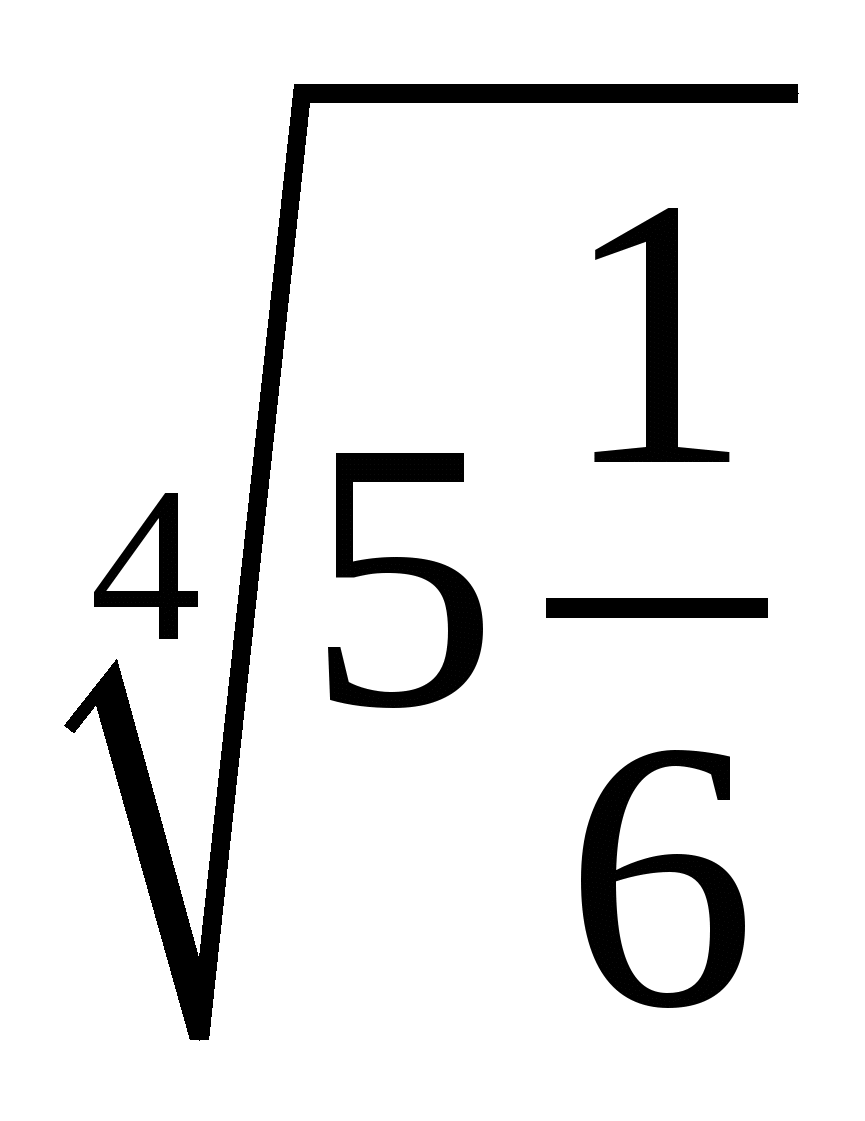
1.Знайти значення виразу
а) 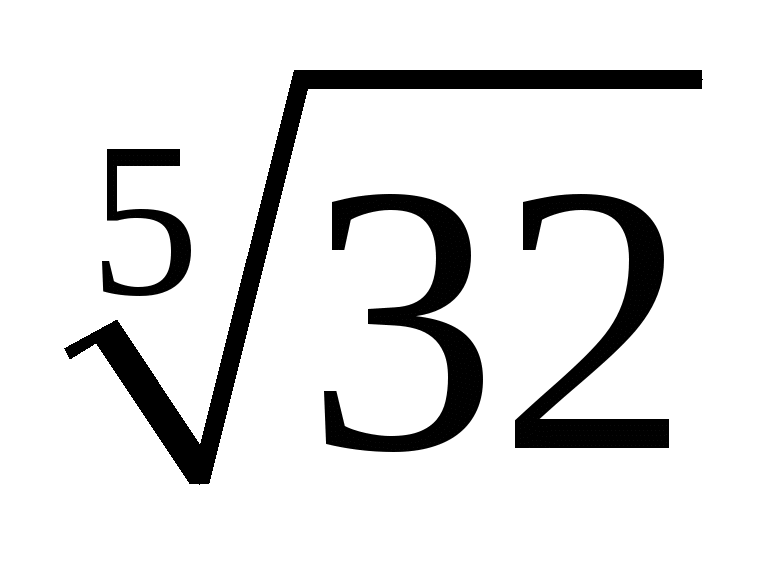
б) 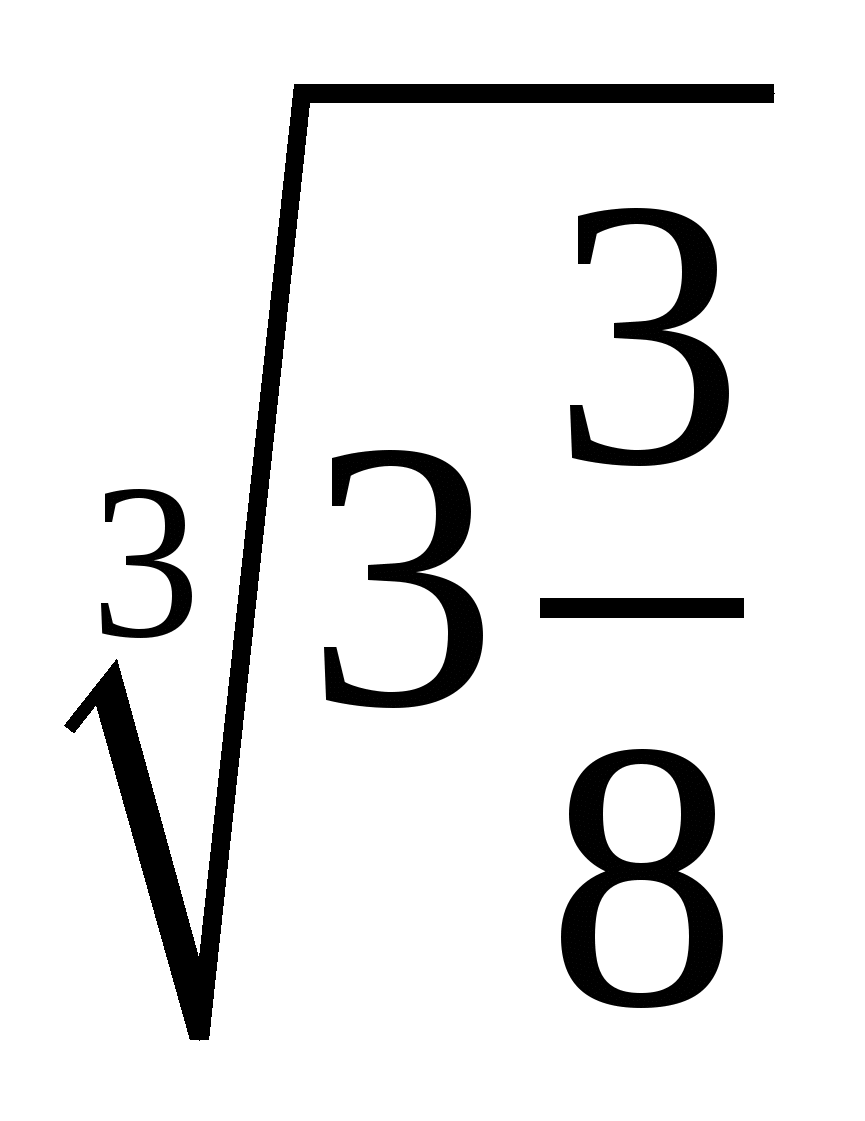
2.Обчислити
а) 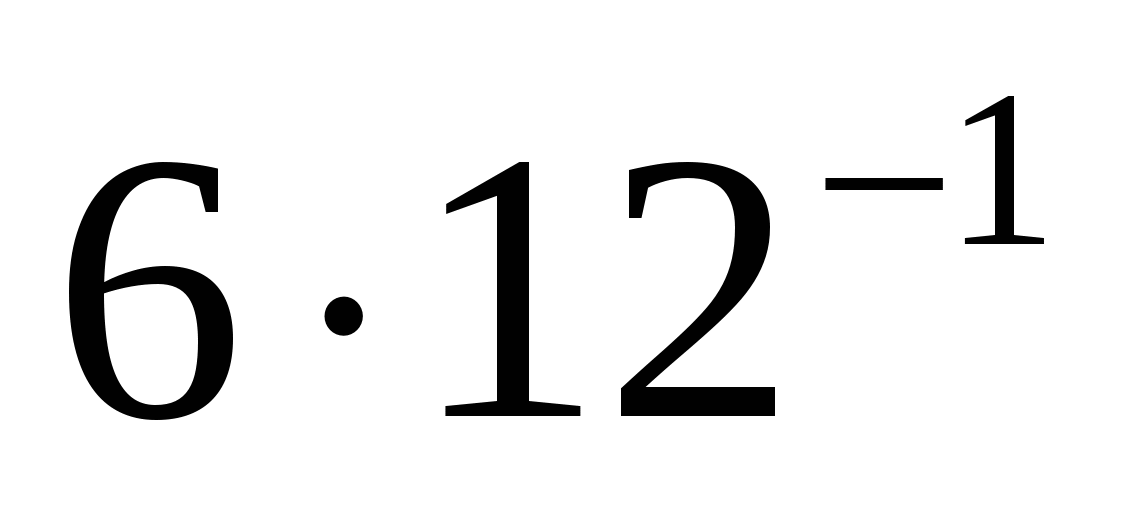
б) 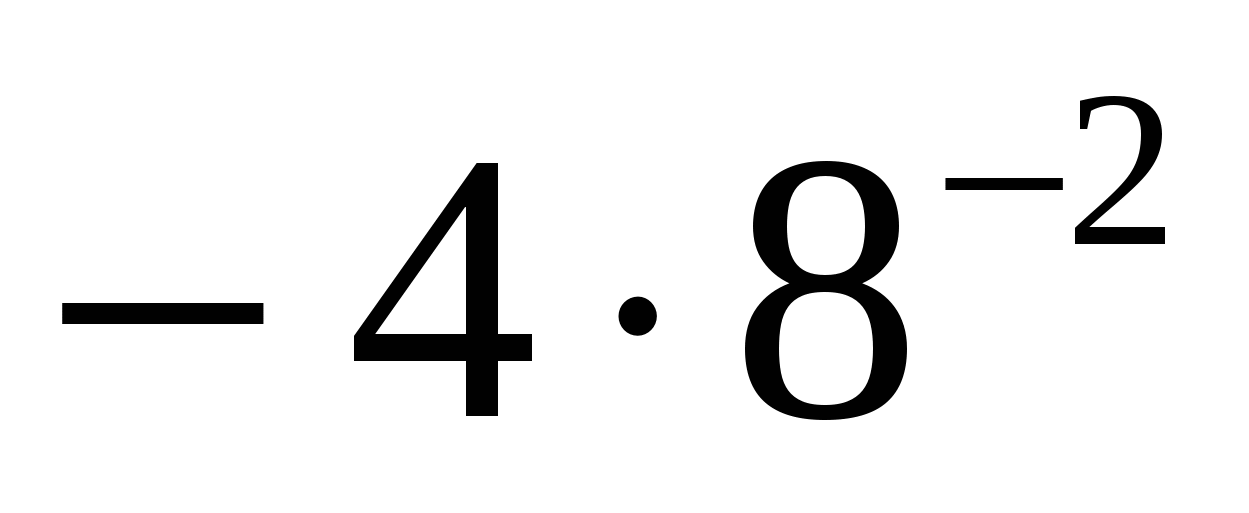
В) 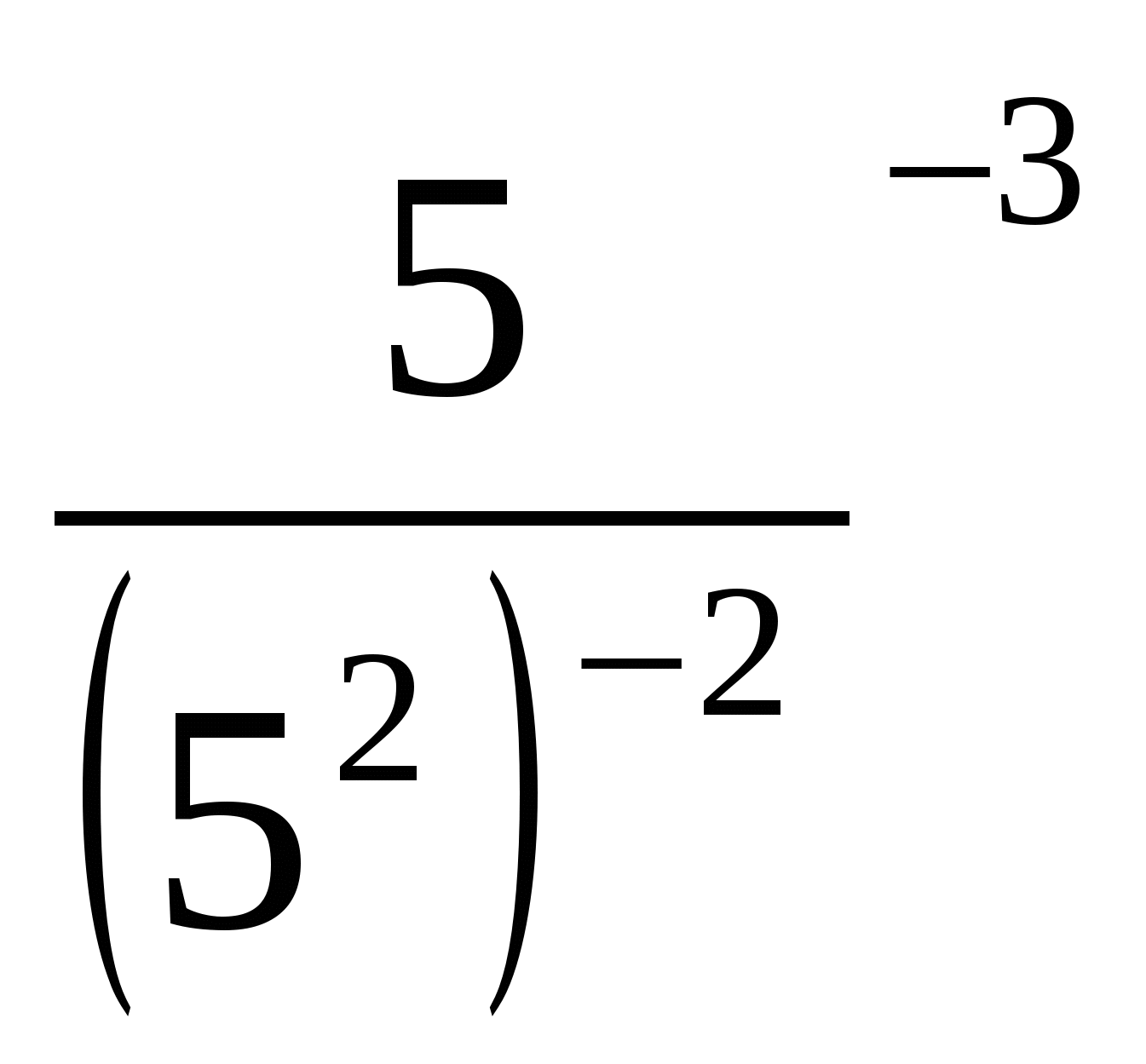
2.Обчислити
а) 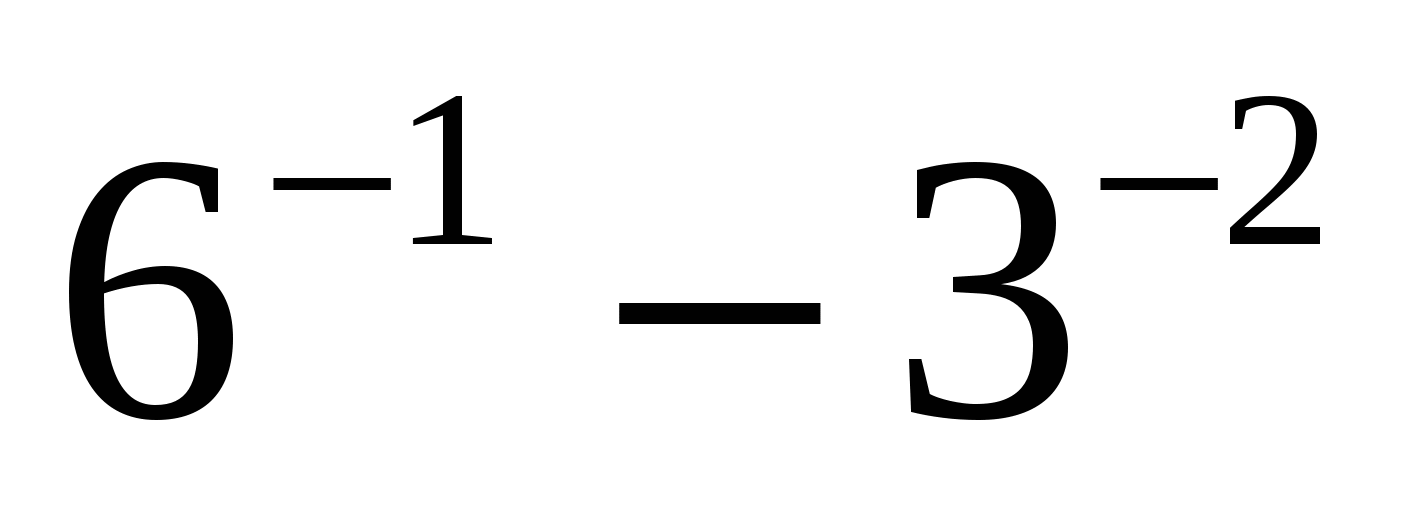
б) 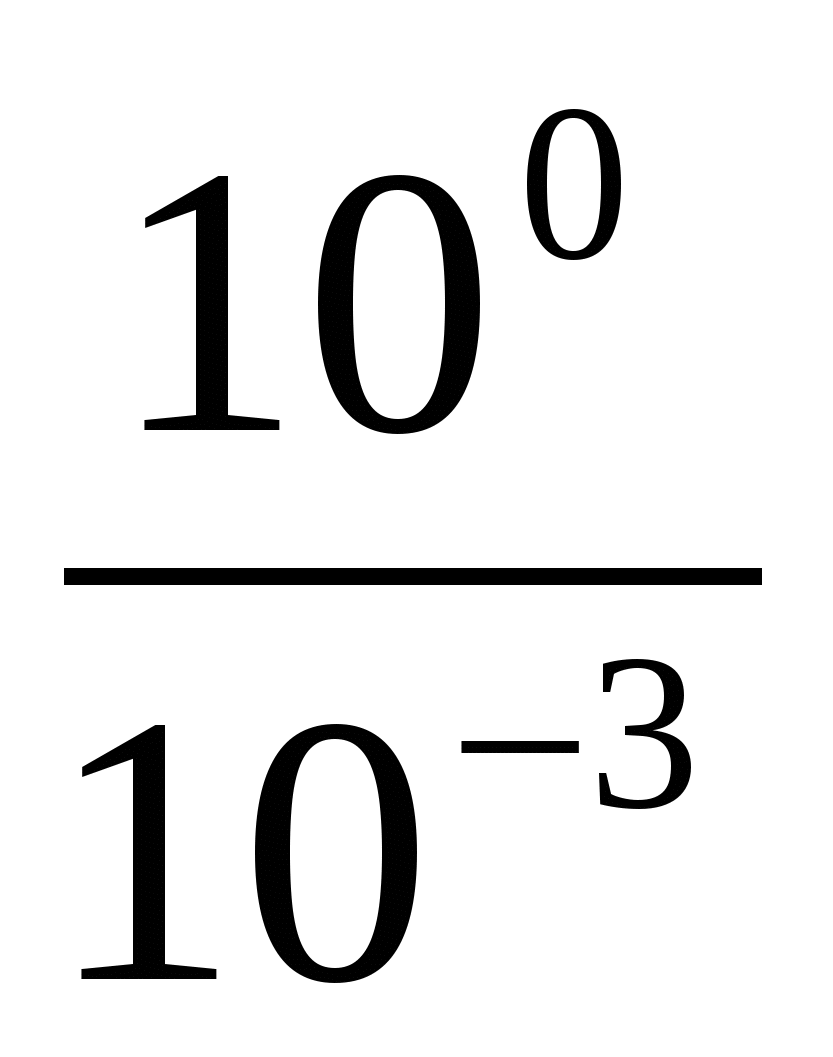
в) 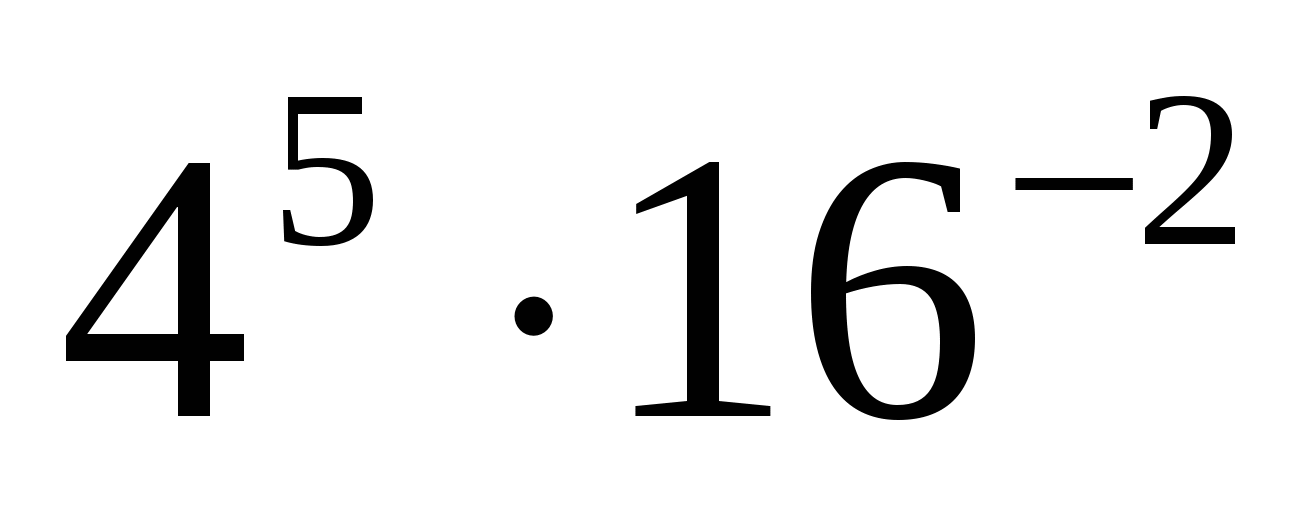
Самоперевірка(На зворотній дошці):
Матриця відповідей:
№ варіанти/завдання
Завдання 1
Завдання 2
Варіант 1
а) 2
б) 2
а) 0,5
б) 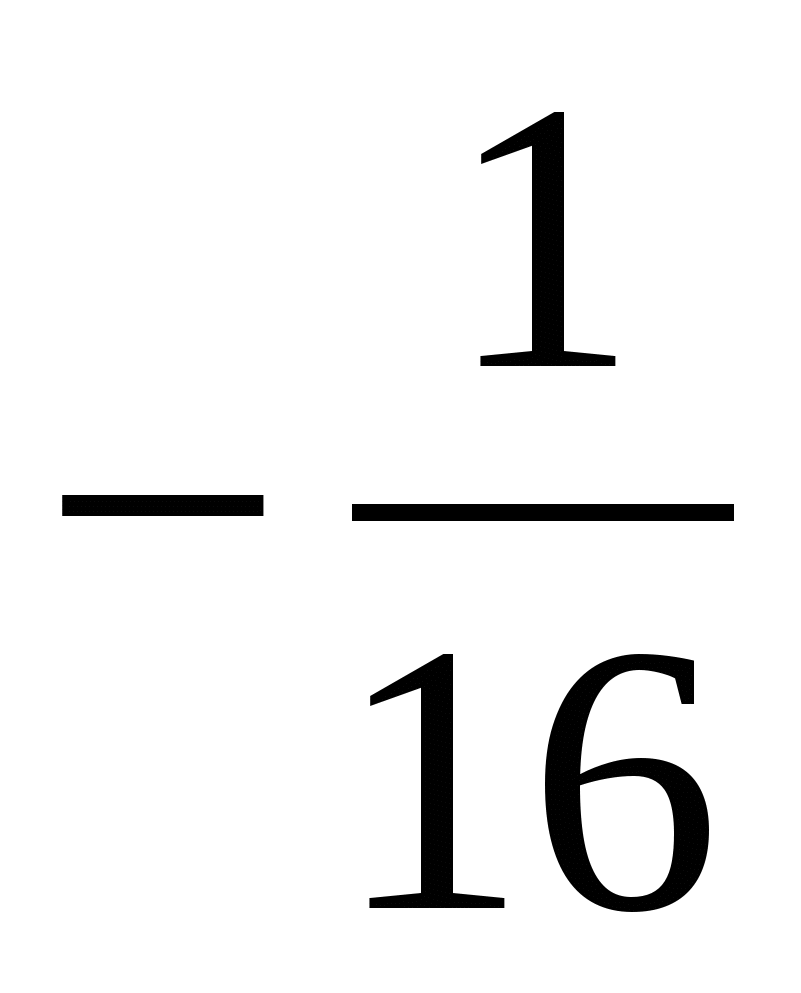
в) 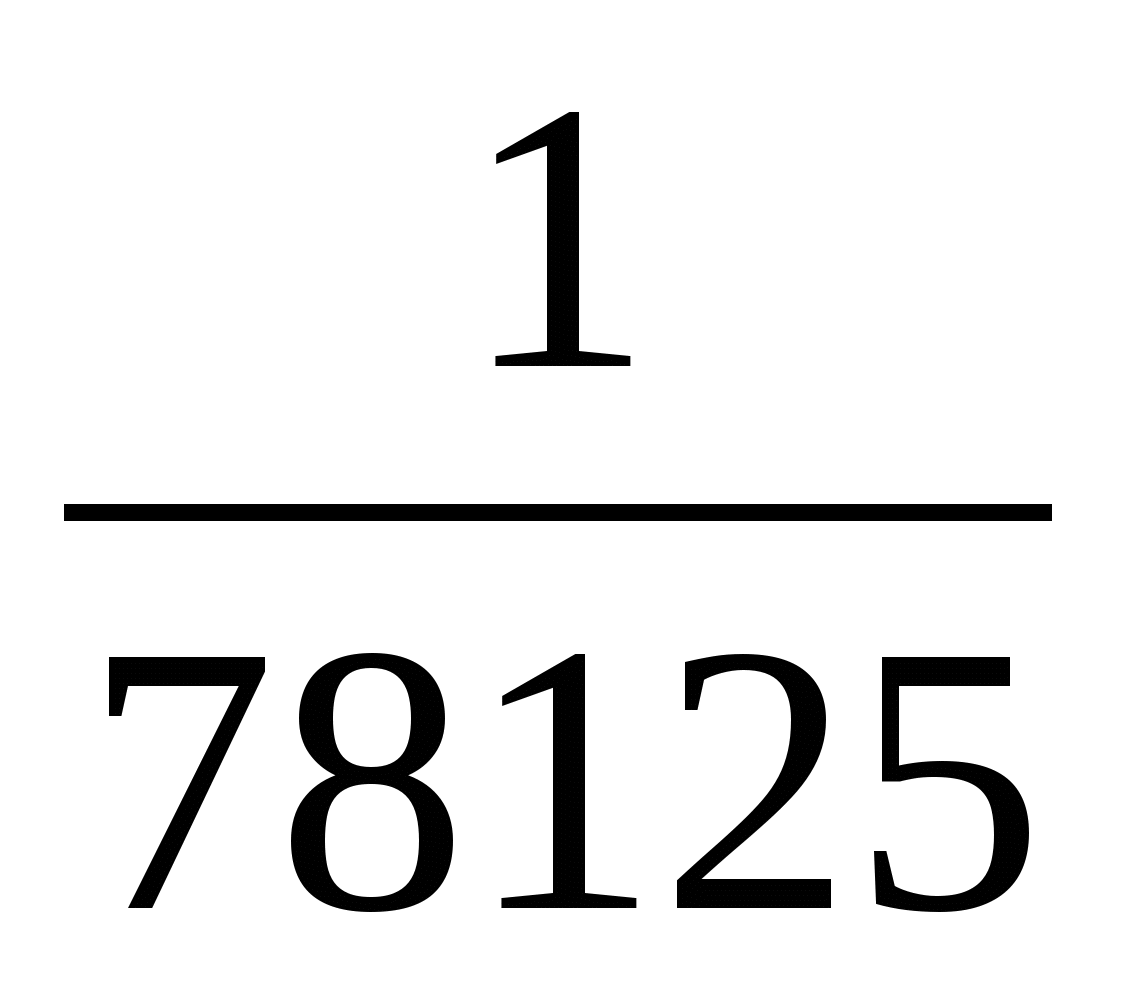
Варіант 2
а) 1,5
б)
а) 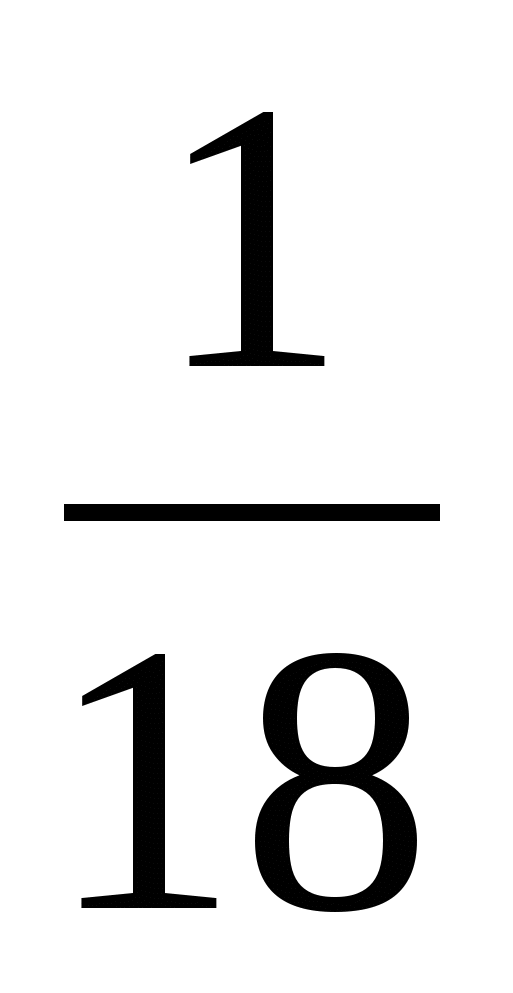
б) 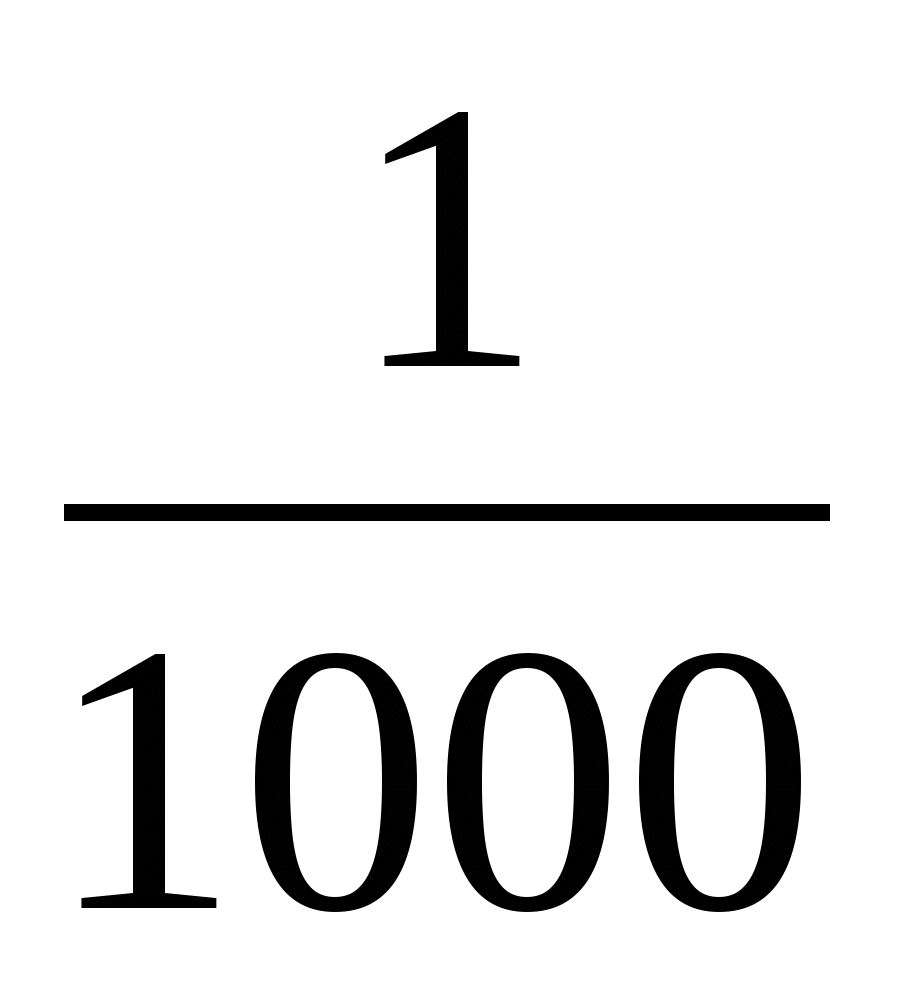
в 4
II. Формування нових знань
Розглянемо, який сенс має вираз, де  - додатне число– дробове число та m-ціле,n-натуральне (n›1)
- додатне число– дробове число та m-ціле,n-натуральне (n›1)
Визначення: ступенем числа a 0 з раціональним показникомr = , m-ціле, n-натуральне ( n›1)називається число.
Отже: 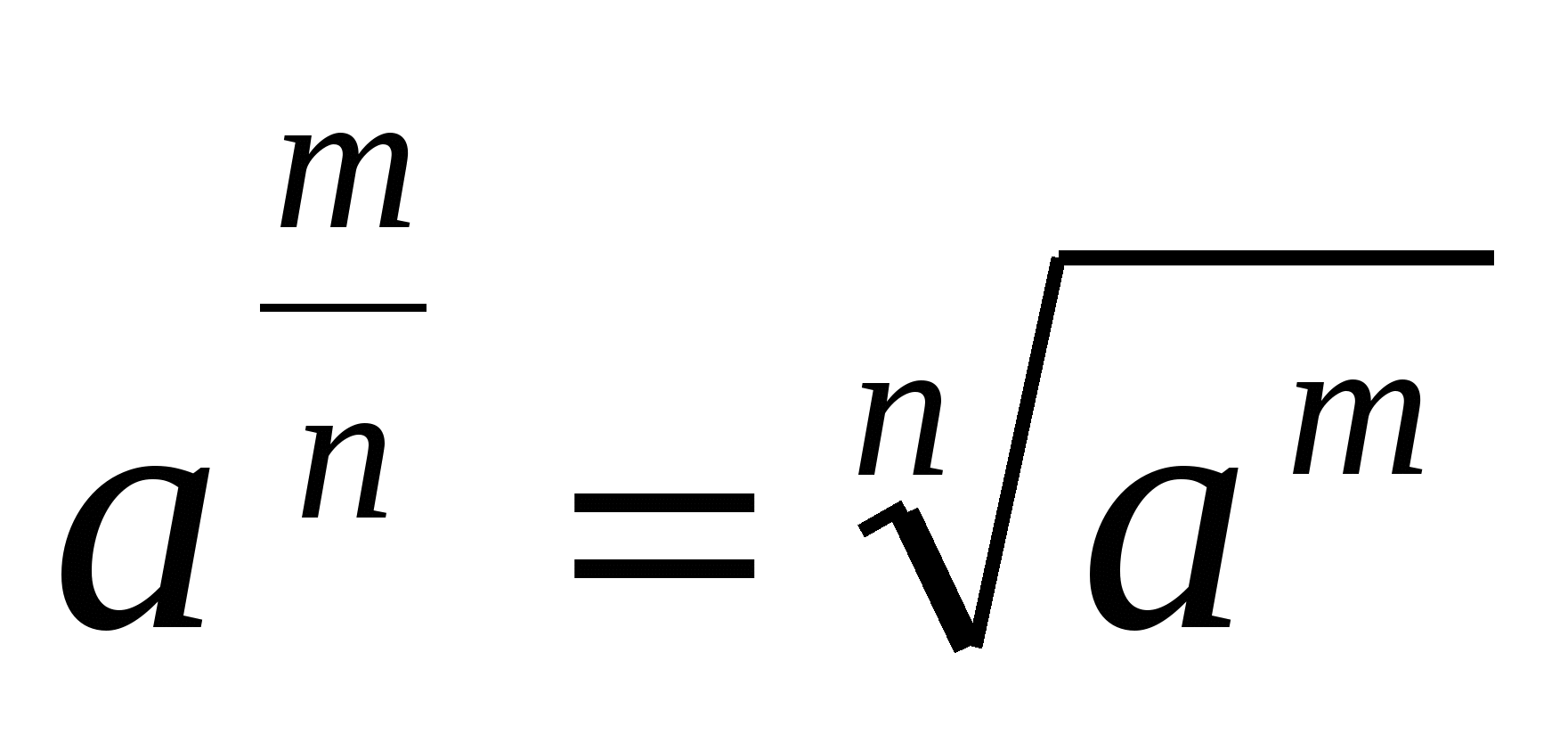
Наприклад: 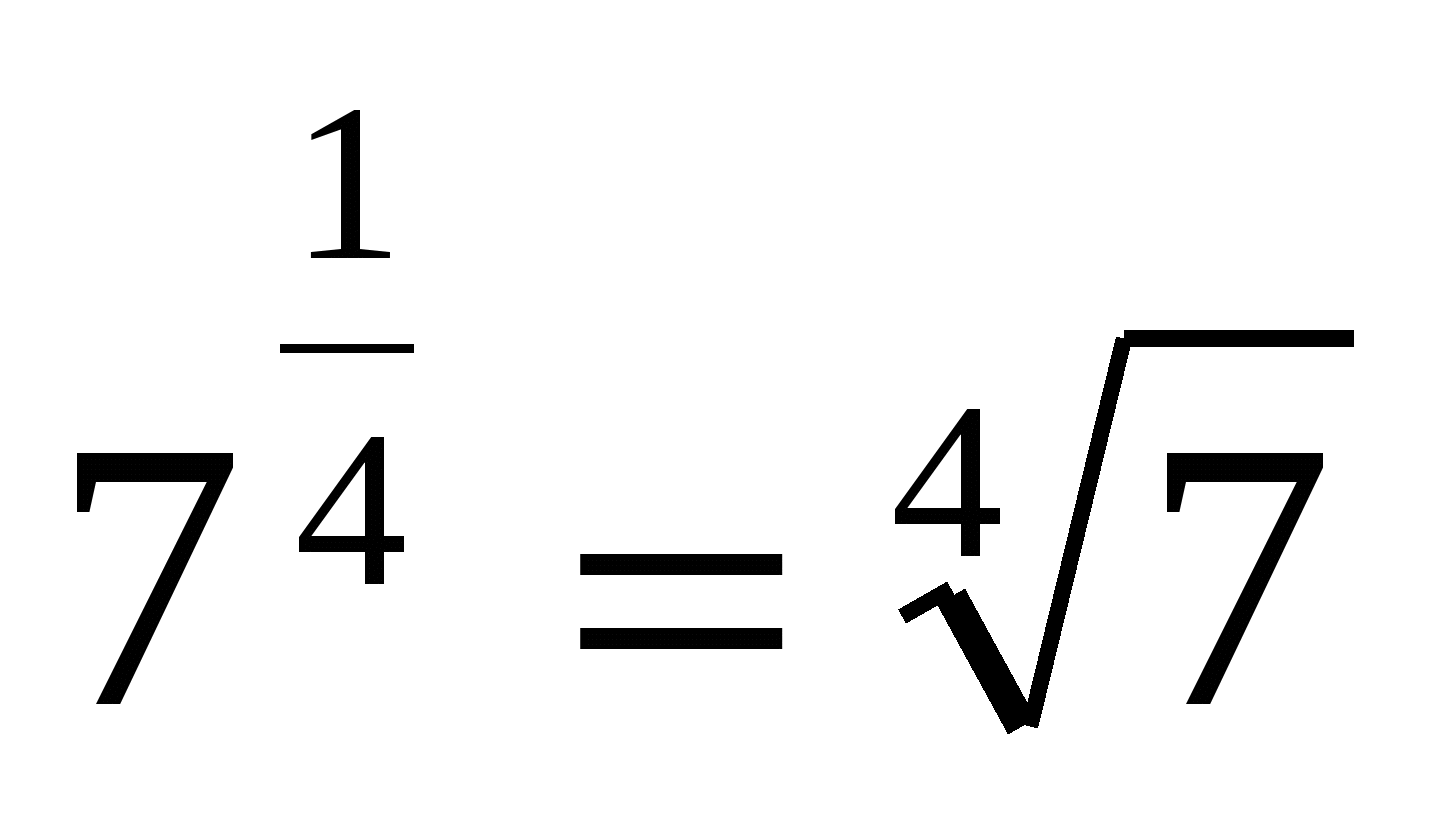
Зауваження:
1. Для будь-якого позитивно a та будь-якого раціонального r число 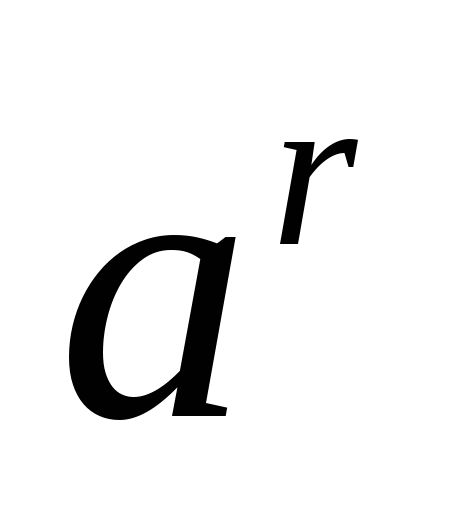 позитивно.
позитивно.
2. При 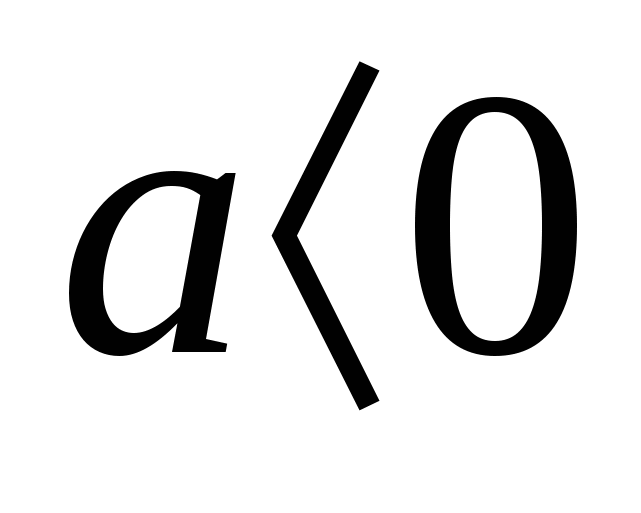 раціональний ступінь числаaне визначається.
раціональний ступінь числаaне визначається.
Такі висловлювання як 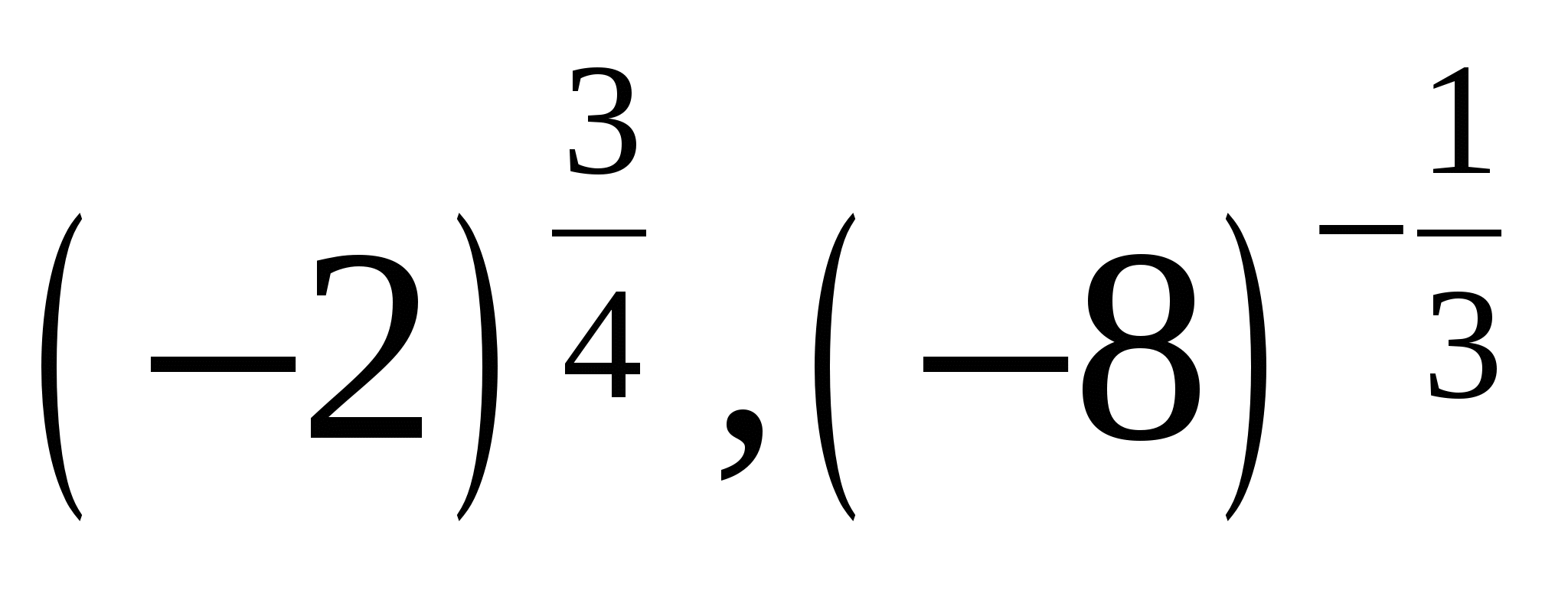 немає сенсу.
немає сенсу.
3.Якщо 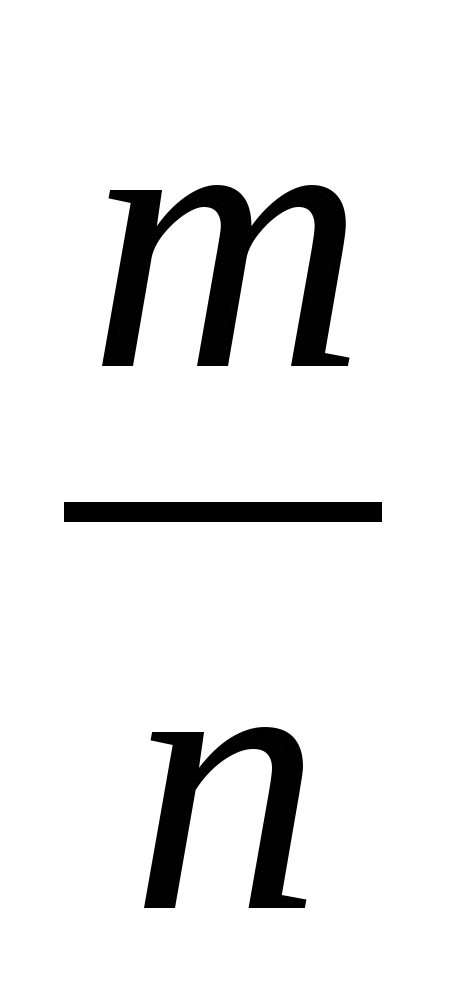 дробове позитивне число те,
дробове позитивне число те, 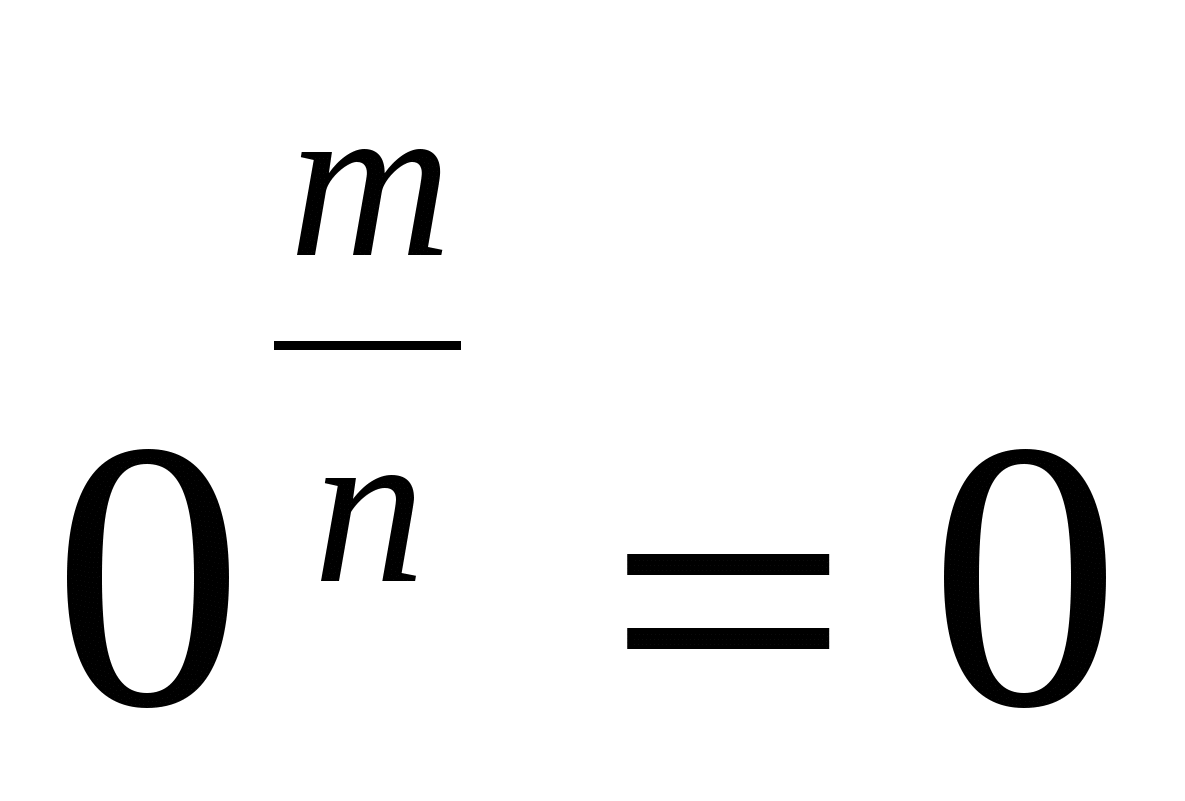 .
.
Якщо 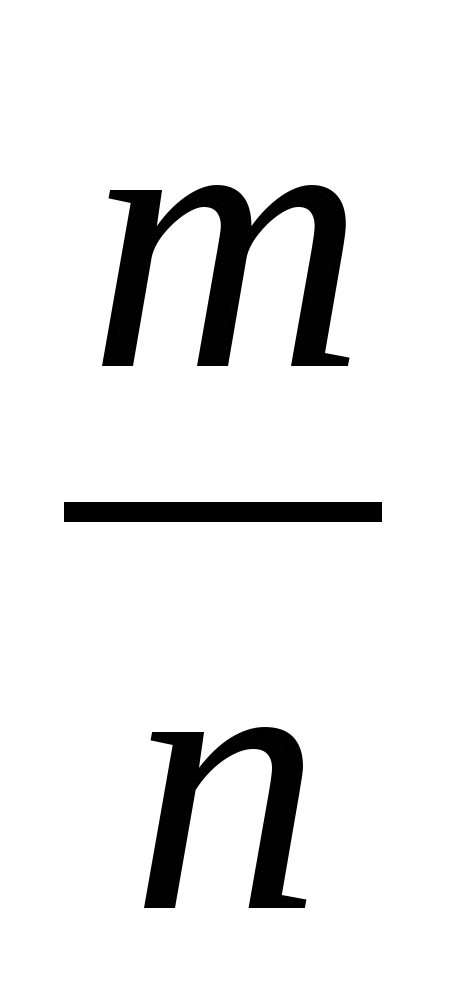 дробове негативне число, то
дробове негативне число, то 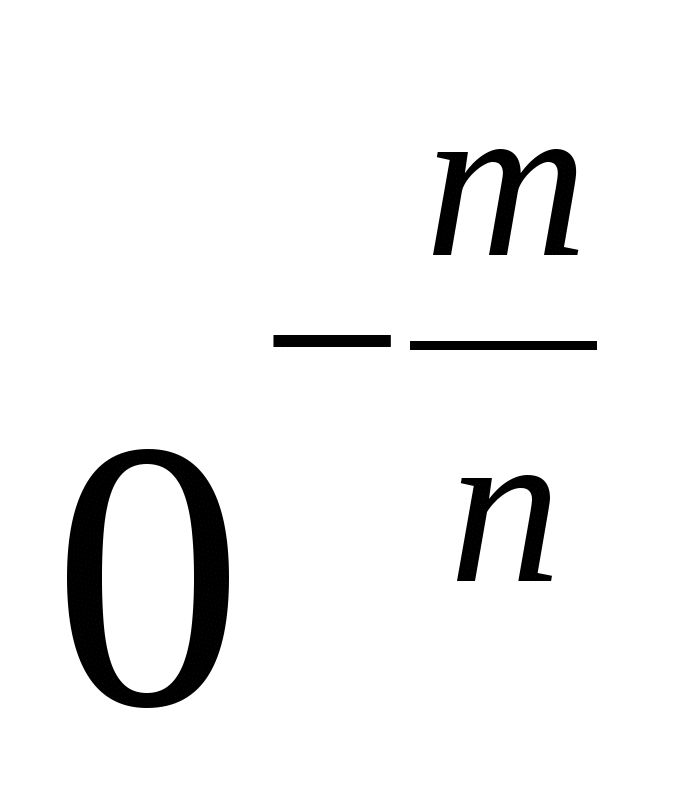 -не має сенсу.
-не має сенсу.
Наприклад: 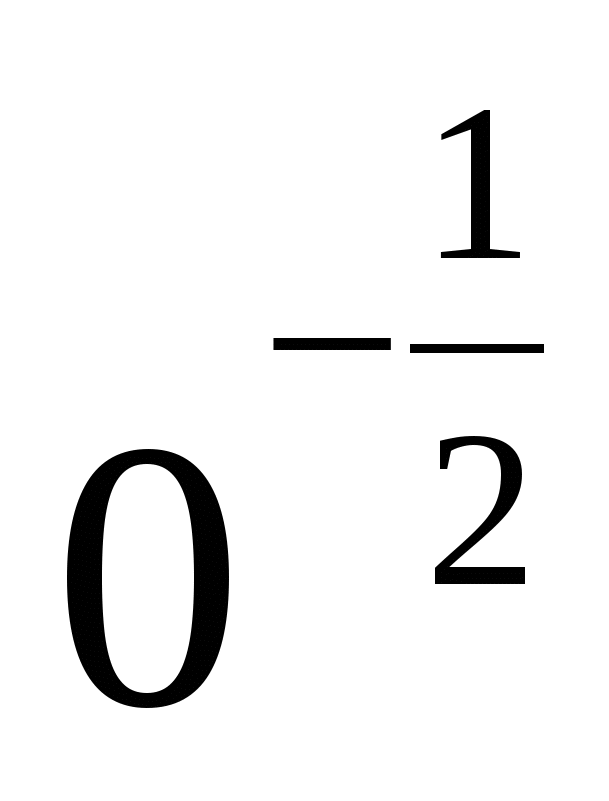 - не має сенсу.
- не має сенсу.
Розглянемо властивості ступеня із раціональним показником.
Нехай a >0, >0; r, s – будь-які раціональні числа. Тоді ступінь з будь-яким раціональним показником має такі властивості:
1.
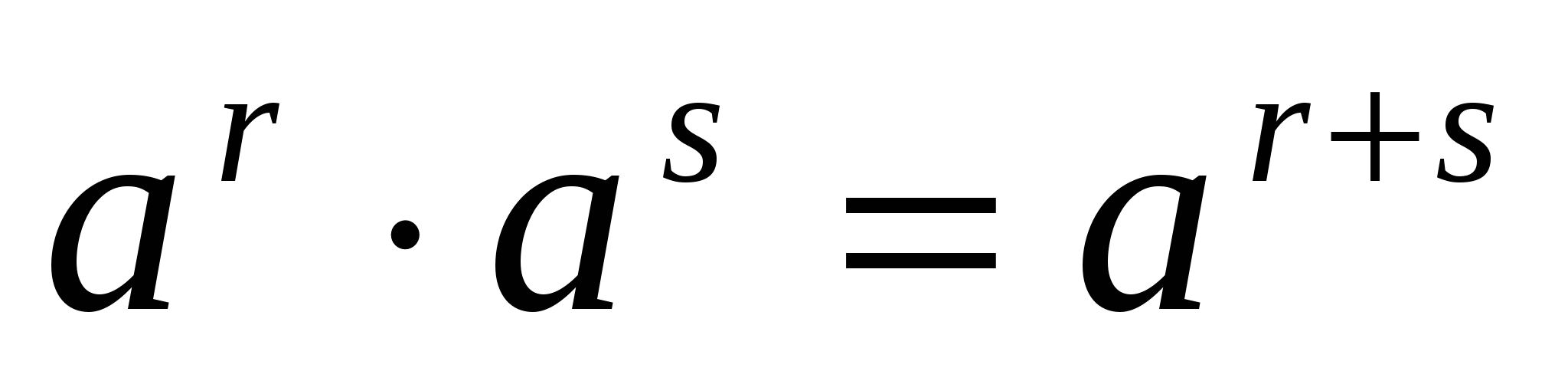 2.
2.
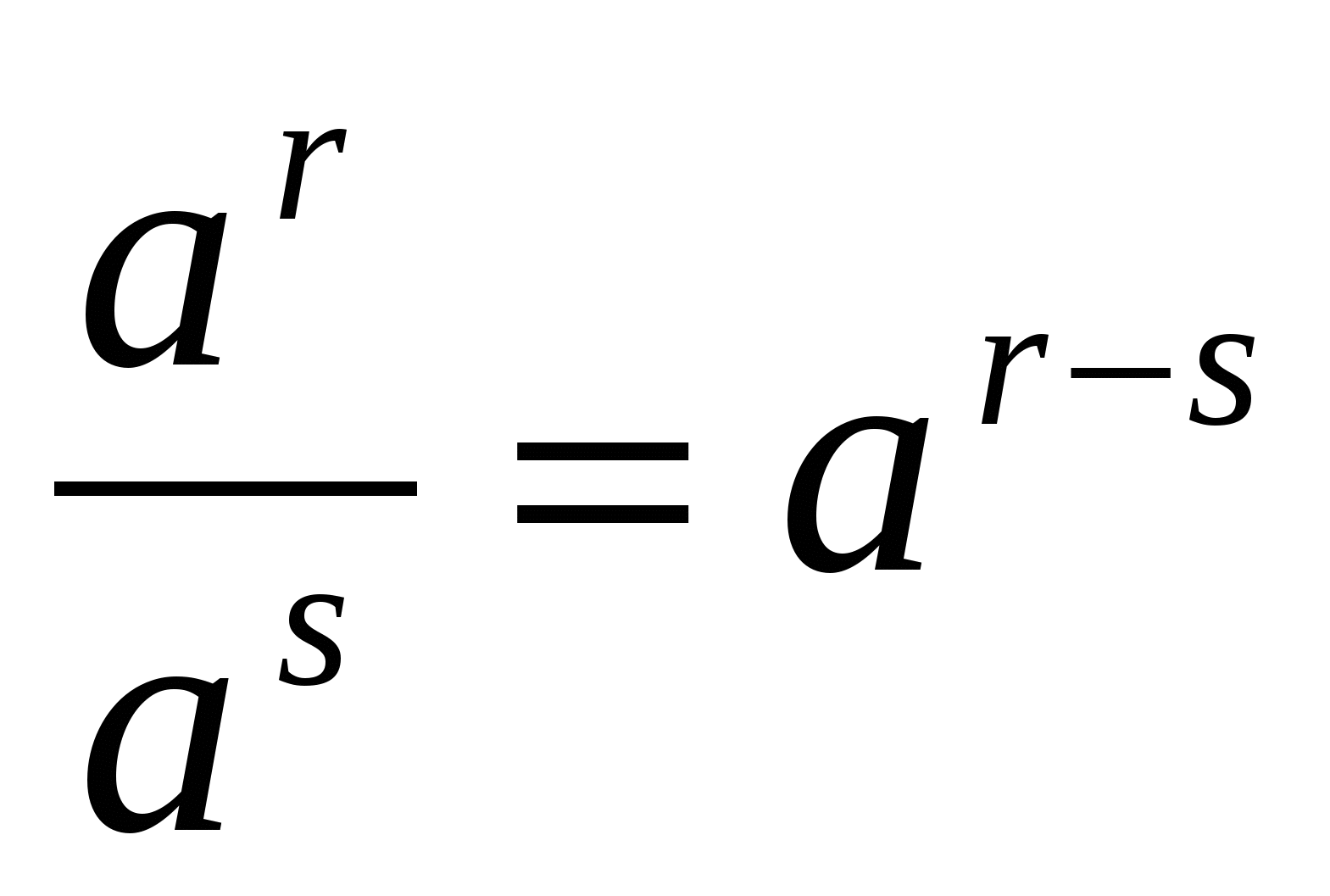 3.
3.
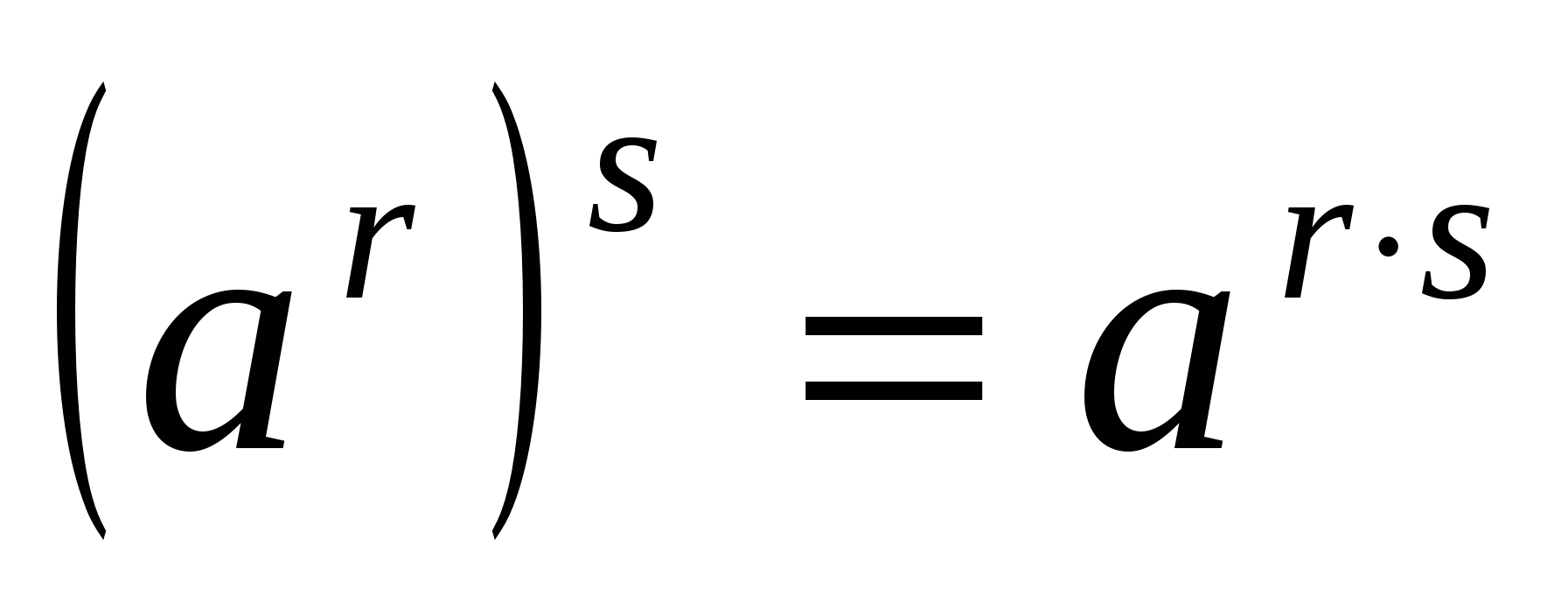 4.
4.
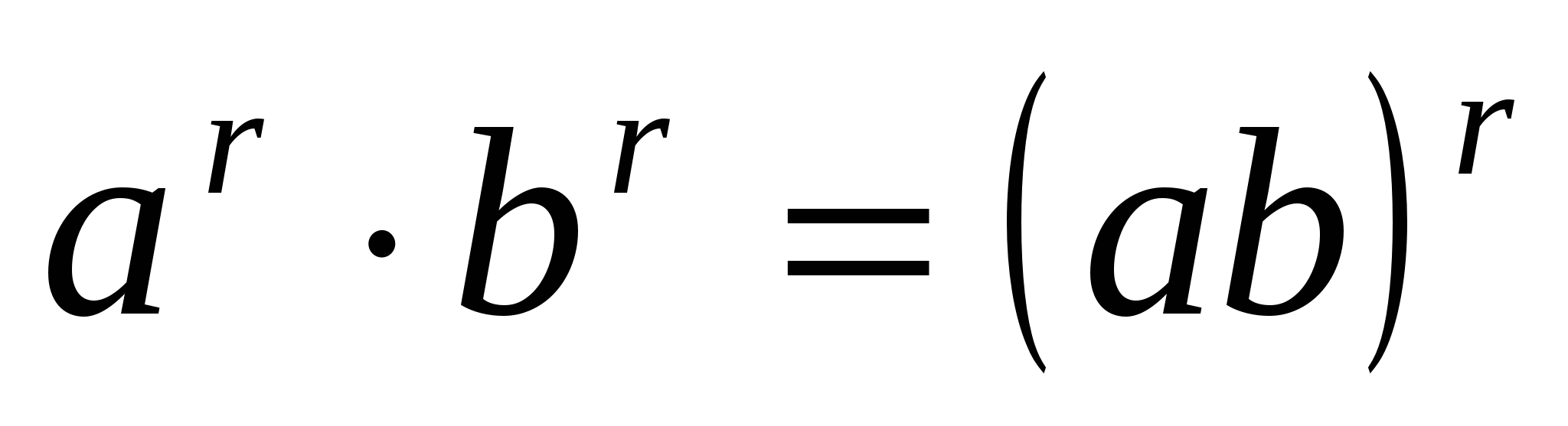 5.
5.
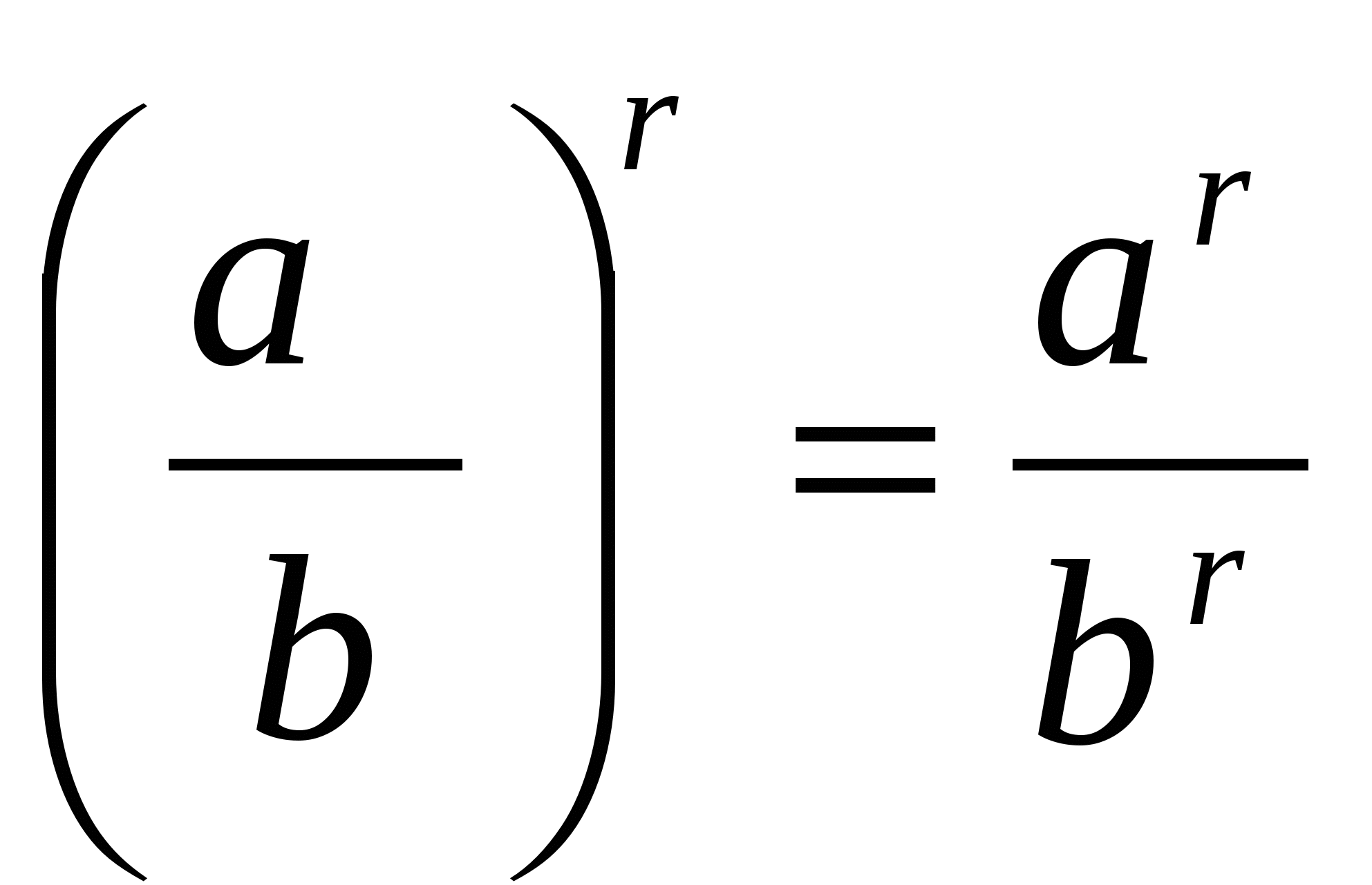
III. Закріплення. Формування нових умінь та навичок.
Картки завдання робота в малих групах у формі тесту.














 Назад вперед
Назад вперед
Увага! Попередній перегляд слайдів використовується виключно для ознайомлення та може не давати уявлення про всі можливості презентації. Якщо вас зацікавила ця робота, будь ласка, завантажте повну версію.
Тип уроку: узагальнюючий урок
Основні поняття. Визначення ступеня з цілим показником та її властивості, визначення кореня п-ого ступеня та його властивості, визначення ступеня з раціональним показником та її властивості, статечна функція та її основні властивості.
Самостійна діяльність учнів.Розв'язання задач на тему "Ступінь з раціональним показником".
Використання нових інформаційних технологій. Як додатковий ілюстративний матеріал показ на інтерактивній дошці презентаціїдо цього уроку.
План уроку
| Етапи уроку | Час, хв | Прийоми та методи |
| I. Етап актуалізації знань. Мотивація навчальної проблеми | 2 | Розмова вчителя |
| ІІ. Основний зміст уроку. Відпрацювання з учнями перетворень алгебраїчних виразів, що містять ступінь з раціональним показником | 40 | Пояснення вчителя. Евристична бесіда |
| ІІІ. Формування умінь та навичок. Відпрацювання вивченого матеріалу | 40 | Розв'язання задач. Відповіді на запитання учнів |
| IV. Первинна перевірка засвоєння знань. Рефлексія | 5 | Повідомлення вчителя. Повідомлення учнів |
| V. Домашнє завдання | 3 | Запис на дошці |
1. Ступінь із цілим показником
Вираз називається ступенем із натуральним показником . Ясно, що Число aназивається підставою ступеня , а n - показником ступеня . Третій ступінь числа називається кубом , друга - квадратом . Першим ступенем називається саме число a.
У параграфі 1.1.2 було визначено поняття ступеня натурального числа із натуральним показником. Узагальним це визначення у разі довільного дійсного числа.
Нехай a- будь-яке дійсне число; n- Натуральне число, більше одиниці. n-й ступенем числа a називається твір nмножників, кожен з яких дорівнює a. Якщо n= 1, то за визначенням вважають, що a 1 = a. Число aназивається підставою ступеня , число n - показником ступеня .
Справедливі такі властивості ступеня:
Наприклад,
За визначенням вважають, що a 0 = 1 для кожного. Нульовий ступінь числа нуль не визначено.
За визначенням вважають, що якщо n- натуральне число, то
Справедлива рівність Наприклад,
Абсолютно аналогічно вводиться поняття ступеня раціональних виразів. Щоб звести раціональний дріб у натуральний ступінь, потрібно окремо звести в цей ступінь чисельник, і окремо - знаменник:
Зведення раціонального дробу в негативний ступінь відбувається за такою формулою:
Перетворити на дріб ступінь
2. Корінь n-й ступеня
Нехай і тоді існує єдине невід'ємне число xтаке, що виконується рівність Це число називається арифметичним коренем n-го ступеня з невід'ємного числа і позначається При цьому число aназивається підкореним числом , а число n - показником кореня .
Замість слова "корінь" часто кажуть радикал . Якщо n= 2, то зазвичай пишуть просто: n= 2 арифметичний корінь називається квадратним коренем , при n= 3 говорять про кубічному корені .
Отже, за визначенням:
Звідси випливає, що, наприклад,
При справедливі такі властивості коренів.
Якщо a < 0, а то не существует такого действительного x, у якому виконувалася рівність Отже, неможливо запровадити поняття кореня парного ступеня з негативного числа. Однак визначити поняття кореня непарного ступеня з негативного числа все ж таки можливо. Справді, нехай a < 0, а n- непарне число, тоді існує однина xтаке, що Це число і називається корінням непарного ступеня з негативного числа . Воно позначається так само: Наприклад, так як Для непарних показників ступеня якості, справедливі для невід'ємних значень підкорених виразів, вірні також і для негативних значень підкорених виразів.
Спростити:
Рішення (Додаток 1)Спростіть вирази 1) 2) 3) Приклад 2a< 0 относятся:
Справедливі такі властивості статечної функції:
Формування умінь та навичок. Відпрацювання вивченого матеріалу
- Відповісти на запитання у вигляді тесту. (Додаток 2)
- Виконати самостійно завдання та вправи.
Ступінь із раціональним показником, її властивості.
Вираз а n визначено для всіх а та n, крім випадку а=0 при n≤0. Нагадаємо властивості таких ступенів.
Для будь-яких чисел а, b та будь-яких цілих чисел m і п справедливі рівності:
A m *a n = a m+n; a m:а n = m-n (а≠0); (а m) n = а mn; (ab) n = n * b n ; (b≠0); а 1 = а; а 0 = 1 (а ≠ 0).
Відзначимо також таку властивість:
Якщо m>n, то m >а n при а>1 і а m<а n при 0<а<1.
У цьому пункті ми узагальним поняття ступеня числа, надавши сенс виразам типу 2 0.3 , 8
5/7 , 4
-1/2 і т. д. Природно при цьому дати визначення так, щоб ступеня з раціональними показниками мали ті ж властивості (або хоча б їх частиною), що й ступеня з цілим показником. Тоді, зокрема, n-й ступінь числаповинна дорівнювати а m . Справді, якщо властивість
(a p) q = a pq
виконується, то
Остання рівність означає (за визначенням кореня n-го ступеня), що числомає бути корінням п-го ступеня з числа а m.
Визначення.
Ступенем числа а>0 із раціональним показником r=, де m — ціле число, а n — натуральне (n > 1), називається число
Отже, за визначенням
(1)
Ступінь числа 0 визначено лише позитивних показників; за визначенням 0 r = 0 для будь-якого r>0.
Ступінь із ірраціональним показником.
Ірраціональне числоможна уявити у виглядімежі послідовності раціональних чисел:
.
Нехай. Тоді існують ступеня з раціональним показником. Можна довести, що послідовність цих ступенів є схожою. Межа цієї послідовності називається ступенем з основою та ірраціональним показником: .
Зафіксуємо позитивне число а і поставимо у відповідність кожному числу. Тим самим одержимо числову функцію f(x) = a x , визначену на безлічі Q раціональних чисел і що має раніше перераховані властивості. При а=1 функція f(x) = a x постійна, тому що 1 x =1 для будь-якого раціонального х.
Нанесемо кілька точок графіка функції у = 2 x попередньо обчисливши за допомогою калькулятора значення 2 x на відрізку [-2; 3] з кроком 1/4 (рис. 1, а), а потім з кроком 1/8 (рис. 1, б). Продовжуючи подумки такі ж побудови з кроком 1/16, 1/32 і т.д. ми бачимо, що точки, що виходять, можна з'єднати плавною кривою, яку природно вважати графіком деякої функції, визначеної і зростаючої вже на всій числовій прямій і приймаючої значенняу раціональних точках(Рис. 1, в). Побудувавши досить велику кількість точок графіка функції, можна переконатися в тому, що аналогічні властивості має і ця функція (відмінність полягає в тому, що функціязменшується на R).
Ці спостереження підказують, що можна визначити числа 2α та для кожного ірраціонального α, що функції, що задаються формулами y=2 x і будуть безперервними, причому функція у = 2 x зростає, а функціяспадає на всій числовій прямій.
Опишемо загалом, як визначається число a α для ірраціональних α при а>1. Ми хочемо досягти того, щоб функція у = a x була зростаючою. Тоді за будь-яких раціональних r 1 і r 2 таких, що r 1<α
Вибираючи значення r 1 та r 2 , що наближаються до х, можна помітити, що відповідні значення a r 1 та a r 2 мало відрізнятимуться. Можна довести, що існує, і притому лише одне, число у, яке найбільше a r 1 для всіх раціональних r 1 і найменше a r 2 для всіх раціональних r 2 . Це число у визначенні є α .
Наприклад, обчисливши за допомогою калькулятора значення 2 x у точках хn і х`n, де хn і х`n - десяткові наближення числами виявимо, що, чим ближче х n і х`n до , тим менше 2 x n і 2 x`n.
Оскільки , то
![]() і, отже,
і, отже,
Аналогічно, розглядаючи такі десяткові наближенняза нестачею та надлишком, приходимо до співвідношень
;
;
;
;
.
Значення обчислене на калькуляторі, таке:
.
Аналогічно визначається число a α для 0<α<1. Кроме того полагают 1
α =1 для будь-якого α та 0α =0 для α>0.
Показова функція.


