Що таке показник кореня? Ступінна функція та коріння, формули та графік

Арифметичний квадратний корінь

Спробуймо розібратися, що це за поняття таке «корінь» і «з чим його їдять». Для цього розглянемо приклади, з якими ти вже стикався на уроках (ну, або тобі з цим тільки доведеться зіткнутися).

Наприклад, маємо рівняння. Яке рішення даного рівняння? Які числа можна звести до квадрата і отримати при цьому? Згадавши таблицю множення, ти легко даси відповідь: і (адже при перемноженні двох негативних чисел виходить позитивне число)! Для спрощення математики ввели спеціальне поняття квадратного кореня і надали йому спеціальний символ.

Дамо визначення арифметичного квадратного кореня.

А чому ж число має бути обов'язково невід'ємним? Наприклад, чому дорівнює. Так-так спробуємо підібрати. Може, три? Перевіримо: , а чи не. Може, ? Знову ж таки, перевіряємо: . Ну що ж, не підбирається? Це й слід було очікувати – бо немає таких чисел, які при зведенні у квадрат дають негативне число!
Це треба запам'ятати: число або вираз під знаком кореня має бути негативним!

Проте найуважніші вже напевно помітили, що у визначенні сказано, що рішення квадратного кореня з числа називається таке невід'ємнечисло, квадрат якого дорівнює». Хтось із вас скаже, що на самому початку ми розбирали приклад, підбирали числа, які можна звести в квадрат і отримати при цьому, відповідь була і, а тут йдеться про якесь «невід'ємне число»! Таке зауваження цілком доречне. Тут необхідно просто розмежувати поняття квадратних рівнянь та арифметичного квадратного кореня у складі. Наприклад, не рівносильне виразу.

З цього випливає, що, тобто або. (Читай тему « »)

А випливає, що.

Звичайно, це дуже плутає, але це необхідно запам'ятати, що знаки є результатом розв'язання рівняння, тому що при вирішенні рівняння ми повинні записати всі ікси, які при підстановці у вихідне рівняння дадуть правильний результат. В наше квадратне рівнянняпідходить як, так і.

Однак, якщо просто витягувати квадратний корінь з чогось, то завжди отримуємо один невід'ємний результат.

А тепер спробуй розв'язати таке рівняння. Вже все не так просто і гладко, правда? Спробуй перебрати числа, може щось і вигорить? Почнемо з самого початку – з нуля: – не підходить, рухаємось далі – менше трьох, теж відкидаємо, а що якщо. Перевіримо: - теж підходить, т.к. це більше трьох. З негативними числами вийде така сама історія. І що тепер робити? Невже перебір нам нічого не дав? Зовсім ні, тепер ми точно знаємо, що відповіддю буде деяке число між і, а також між і. Крім того, очевидно, що рішення не будуть цілими числами. Понад те, вони є раціональними. І що далі? Давай побудуємо графік функції та відзначимо на ньому рішення.

Давай спробуємо обдурити систему та отримати відповідь за допомогою калькулятора! Виймемо корінь з, діл-те! Ой-ой-ой, виходить, що. Таке число ніколи не закінчується. Як же таке запам'ятати, адже на іспиті калькулятора не буде! Все дуже просто, це не треба запам'ятовувати, необхідно пам'ятати (або вміти швидко прикинути) приблизне значення. і вже самі собою відповіді. Такі числа називаються ірраціональними, саме для спрощення запису таких чисел і було запроваджено поняття квадратного кореня.

Розглянемо ще один приклад для закріплення. Розберемо таке завдання: тобі потрібно перетнути по діагоналі квадратне поле зі стороною кілометрів, скільки кілометрів тобі належить пройти?

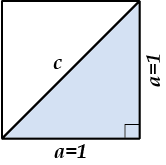
Найочевидніше тут розглянути окремо трикутник і користуватися теоремою Піфагора: . Таким чином, . То чому ж тут однакова відстань? Вочевидь, що відстань може бути негативним, отримуємо, що. Корінь із двох приблизно дорівнює, але, як ми помітили раніше, вже є повноцінною відповіддю.

Щоб вирішення прикладів з корінням не викликало проблем, необхідно їх бачити та впізнавати. Для цього необхідно знати щонайменше квадрати чисел від до, а також вміти їх розпізнати. Наприклад, треба зазначити, що у квадраті одно, і навіть, навпаки, що - це квадраті.

Вловив, що таке квадратне коріння? Тоді вирішуй кілька прикладів.

приклади.

Ну як, вийшло? Тепер давай подивимося такі приклади:

Відповіді:

Кубічний корінь

Ну що ж, з поняттям квадратного кореня начебто розібралися, тепер постараємося розібратися, що таке кубічний корінь і в чому їхня відмінність.

Кубічний корінь із деякого числа - це число, куб якого дорівнює. Помітили, що тут все набагато простіше? Тут немає жодних обмежень на можливі значення як значення під знаком кубічного кореня, Так і числа. Тобто кубічний корінь можна витягти з числа: .

Вловили, що таке кубічний корінь і як його добувати? Тоді наперед вирішувати приклади.

приклади.

Відповіді:

Корінь - ой ступеня

Що ж, ми розібралися з поняттями квадратного та кубічного кореня. Тепер узагальним отримані знання поняттям корінь -ого ступеня.

Корінь ступеняу складі — це число, -ая ступінь якого дорівнює, тобто.

рівносильно.

Якщо - парно, то:

• при негативному, вираз не має сенсу (коріння парного ступеня з негативних чисел витягти не можна!);
• при невід'ємному() вираз має один не негативний корінь.

Якщо - непарно, то вираз має єдиний корінь за будь-якого.

Не лякайтеся, тут діють такі ж принципи, що і з квадратним і кубічним корінням. Тобто принципи, які ми застосовували під час розгляду квадратного коріння, поширюємо на всі корені парного ступеня.

А ті властивості, які застосовували для кубічного кореня, поширюються на корені непарного ступеня.

Ну що, стало зрозуміліше? Давайте розбиратися на прикладах:

Тут все більш-менш зрозуміло: спочатку дивимося - ага, ступінь - парна, під коренем число позитивне, значить наше завдання - знайти таке число, четвертий ступінь якого дасть нам. Ну є припущення? Може, ? Точно, !

Так, ступінь дорівнює - непарна, під коренем число негативне. Наше завдання – знайти таке число, при зведенні якого у ступінь виходить. Відразу помітити корінь досить складно. Однак можна відразу звузити область пошуку, правда? По-перше, безумовно шукане число негативно, а по-друге, можна побачити, що - непарне, отже, і шукане число - непарне. Спробуй підібрати коріння. Звичайно, і можна сміливо відкидати. Може, ?

Так, це те, що ми шукали! Зауваж, що з спрощення розрахунку ми користувалися властивостями ступенів: .

Основні властивості коренів

Зрозуміло? Якщо ні, то розглянувши приклади, все має стати на свої місця.

Розмноження коренів

Як множити коріння? На це питання допомагає відповісти найпростіша та базова властивість:

Почнемо з простенького:

Коріння з чисел, що виходять, рівно не витягуються? Не біда – ось вам такі приклади:

А якщо множників не два, а більше? Теж саме! Формула множення коренів працює з будь-якою кількістю множників:

Що ми можемо зробити з ним? Ну звичайно, сховати трійку під коренем, пам'ятаючи при цьому, що трійка - корінь квадратний!

Навіщо нам це потрібне? Так просто, щоб розширити наші можливості при вирішенні прикладів:

Як тобі така властивість коріння? Істотно спрощує життя? На мене, так точно! Тільки треба пам'ятати, що вносити під знак кореня парного ступеня ми можемо лише позитивні числа.

Подивимося, де це ще може стати в нагоді. Наприклад, у задачі вимагають порівняти два числа:

Що більше:

Відразу і не скажеш. Ну що, скористаємось розібраною властивістю внесення числа під знак кореня? Тоді вперед:

Ну і, знаючи, що чим більше число під знаком кореня, тим більше корінь! Тобто. якщо, отже, . Звідси твердо робимо висновок, що. І ніхто не переконає нас у протилежному!

До цього ми вносили множник під знак кореня, як його винести? Потрібно просто розкласти його на множники і витягти те, що витягується!

Можна було піти іншим шляхом і розкласти на інші множники:

Непогано, правда? Будь-який із цих підходів вірний, вирішуй як тобі зручно.

Ось, наприклад, такий вираз:

У цьому прикладі міра парна, а якщо вона буде непарна? Знову ж таки, застосуй властивості ступеня і розклади всі на множники:

З цим начебто все ясно, а от як витягти корінь з-поміж ступеня? Ось, наприклад, таке:

Досить просто, правда? А якщо ступінь більший за два? Дотримуємося тієї ж логіки, використовуючи властивості ступенів:

Ну як усе зрозуміло? Тоді такий приклад:

Це підводне каміння, про них завжди варто пам'ятати. Це і є відображення на прикладах якості:

при непарних: при парних та:

Зрозуміло? Закріплюй на прикладах:

Ага, бачимо, корінь парною мірою, негативне число під коренем теж парною мірою. Ну і те саме виходить? А ось що:

От і все! Тепер такі приклади:

Вловив? Тоді наперед вирішувати приклади.

приклади.

Відповіді.

Якщо отримав відповіді, можна зі спокійною душею рухатися далі. Якщо ні, то давай розберемося в цих прикладах:

Подивимося на дві інші властивості коріння:

Ці властивості обов'язково треба розбирати у прикладах. Ну що, займемося цим?

Розібрався? Давай закріпимо.

приклади.

Цілі уроку:

Освітня: створити умови на формування в учнів цілісного ставлення до корені n-ой ступеня, навичок свідомого і оптимального використання властивостей кореня під час вирішення різноманітних завдань.

Розвиваюча: створити умови у розвиток алгоритмічного, творчого мислення, розвивати навички самоконтролю.

Виховні: сприяти розвитку інтересу до предмета, активності, виховувати акуратність у роботі, вміння висловлювати власну думку, давати рекомендації.

Хід уроку

1. Організаційний момент.

Добридень! Добрий час!

Як я рада вас бачити.

Продзвенів уже дзвінок

Починається урок.

Усміхнулися. Дорівнювали.

Один на одного подивилися

І тихенько дружно сіли.

2. Мотивація уроку.

Видатний французький філософ, вчений Блез Паскаль стверджував: «Величність людини в її здатності мислити». Сьогодні спробуємо відчути себе великими людьми, відкриваючи знання собі. Девізом до сьогоднішнього уроку будуть слова давньогрецького математика Фалеса:

Що є найбільше у світі? - простір.

Що найшвидше? - Розум.

Що наймудріше? – Час.

Що найприємніше? - Досягти бажаного.

Хочеться, щоб кожен із вас на сьогоднішньому уроці досягнув бажаного результату.

3. Актуалізація знань.

1. Назвіть взаємозворотні операції алгебри над числами. (Складання та віднімання, множення та розподіл)

2. Чи завжди можна виконати таку операцію алгебри, як розподіл? (Ні, ділити на нуль не можна)

3. Яку ще операцію ви можете виконувати з числами? (Зведення в ступінь)

4. Яка операція їй буде зворотною? (Вилучення кореня)

5. Корінь якого ступеня ви можете отримати? (Корінь другого ступеня)

6. Які властивості квадратного кореня ви знаєте? (Вилучення квадратного кореня з твору, з приватного, з кореня, зведення в ступінь)

7. Знайдіть значення виразів:

З історії.Ще 4000 років тому вавилонські вчені склали поряд з таблицями множення та таблицями зворотних величин (за допомогою яких розподіл чисел зводилося до множення) таблиці квадратів чисел та квадратних коренів чисел. При цьому вони вміли знаходити приблизно значення квадратного кореня з будь-якого цілого числа.

4. Вивчення нового матеріалу.

Очевидно, що відповідно до основних властивостей ступенів з натуральними показниками, з будь-якого позитивного числа існує два протилежні значення кореня парного ступеня, наприклад, числа 4 і -4 є корінням квадратним з 16, так як (-4) 2 = 42 = 16, а числа 3 і -3 є корінням четвертого ступеня з 81, так як (-3) 4 = З4 = 81.

Крім того, немає кореня парного ступеня з негативного числа, оскільки парний ступінь будь-якого дійсного числаневід'ємна. Що ж до кореня непарного ступеня, то для будь-якого дійсного числа існує тільки один корінь непарного ступеня з цього числа. Наприклад, 3 є корінь третього ступеня з 27, оскільки З3 = 27, а -2 є корінь п'ятого ступеня з -32, оскільки (-2) 5 = 32.

У зв'язку з існуванням двох коренів парного ступеня з позитивного числа, введемо поняття арифметичного кореня, щоб усунути цю двозначність кореня.

Невід'ємне значення кореня n-го ступеняз негативного числа називається арифметичним коренем.

Позначення: - корінь n-йступеня.

Число n називається ступенем арифметичного кореня. Якщо n = 2, то рівень кореня не вказується і пишеться. Корінь другого ступеня прийнято називати квадратним, а корінь третього ступеня – кубічним.

B, b2 = а, а ≥ 0, b ≥ 0

B, bп = а, п - парне а ≥ 0, b ≥ 0

п - непарне а, b - будь-які

Властивості

1. , а ≥ 0, b ≥ 0

2. , а ≥ 0, b >0

3. , а ≥ 0

4. , m, n, k - натуральні числа

5. Закріплення нового матеріалу.

Усна робота

а) Які висловлювання мають сенс?

Вирішити №3, 4, 7, 9, 11.

6. Фізкультхвилинка.

У всіх справах помірність потрібна,

Нехай буде основним правилом вона.

Гімнастикою займися, якщо думав довго,

Гімнастика не виснажує тіла,

Але очищає організм повністю!

Заплющте очі, розслабте тіло,

Уявіть – ви птахи, ви раптом полетіли!

Тепер в океані дельфіном пливете,

Тепер у саду яблука стиглі рветься.

Ліворуч, праворуч, довкола подивилися,

Розплющили очі, і знову за справу!

7. Самостійна робота.

Робота у парах с. 178 №1, №2.

8. Д/з.Вивчити п.10 (с.160-161), вирішити № 5, 6, 8, 12, 16 (1, 2).

9. Підсумки уроку. Рефлексія діяльності.

Чи досягнув урок своєї мети?

Чого ви навчилися?

Тоді постає наступне логічне питання: «Яке число всіх квадратних коренів з даного невід'ємного числа a – один, два, три, або ще більше»? Ось відповідь на нього: якщо a дорівнює нулю, то єдиним квадратним коренем із нуля є нуль; якщо ж a – деяке позитивне число, то кількість квадратних коренів із числа a дорівнює двом, причому коріння є . Обґрунтуємо це.

Почнемо з нагоди a=0 . Спочатку покажемо, що нуль справді є квадратним коренем із нуля. Це з очевидної рівності 0 2 =0·0=0 визначення квадратного кореня.

Тепер доведемо, що 0 – єдиний квадратний корінь із нуля. Скористаємося методом від неприємного. Припустимо, що існує деяке число b відмінне від нуля, яке є квадратним коренем з нуля. Тоді має виконуватися умова b 2 =0 , що неможливо, тому що при будь-якому відмінному від нуля b значення виразу b 2 є позитивним. Ми дійшли суперечності. Це доводить, що 0 – єдиний квадратний корінь із нуля.

Переходимо до випадків, коли a – позитивне число. Вище ми сказали, що завжди існує квадратний корінь з будь-якого невід'ємного числа, нехай квадратним коренем a є число b . Припустимо, що є число c , яке також є квадратним коренем з a . Тоді за визначенням квадратного кореня справедливі рівність b 2 =a і c 2 =a , з них випливає, що b 2 −c 2 =a−a=0 , але оскільки b 2 −c 2 =(b−c)·( b+c) , то (b-c) · (b + c) = 0 . Отримана рівність у силу властивостей дій із дійсними числамиможливо лише тоді, коли b-c=0 , або b+c=0 . Таким чином, числа b та c або рівні, або протилежні.

Якщо ж припустити, що є число d , що є ще одним квадратним коренем у складі a , то міркуваннями, аналогічними вже наведеним, доводиться, що d одно чи числу b , чи числу c . Отже, число квадратних коренів із позитивного числа дорівнює двом, причому квадратне коріння є протилежними числами.

Для зручності роботи з квадратним корінням негативний корінь «відокремлюється» від позитивного. З цією метою вводиться визначення арифметичного квадратного кореня.

Визначення.

Арифметичний квадратний корінь з негативного числа a- Це невід'ємне число, квадрат якого дорівнює a.

Для арифметичного квадратного кореня у складі a прийнято позначення . Знак називається знаком арифметичного квадратного кореня. Його також називають знаком радикалу. Тому можна частину чути як «корінь», так і «радикал», що означає той самий об'єкт.

Число під знаком арифметичного квадратного кореня називають підкореним числом, а вираз під знаком кореня – підкореним виразом, при цьому термін «підкорене число» часто замінюють на « підкорене вираз». Наприклад, у записі число 151 – це підкорене число, а запису вираз a є підкореним виразом.

При читанні слово "арифметичний" часто опускається, наприклад, запис читають як "квадратний корінь із семи цілих двадцяти дев'яти сотих". Слово «арифметичний» вимовляють лише тоді, коли хочуть особливо наголосити, що йдеться саме про позитивне квадратне коріння з числа.

У світлі введеного позначення визначення арифметичного квадратного кореня слід, що й у будь-якого неотрицательного числа a .

Квадратне коріння з позитивного числа a за допомогою знака арифметичного квадратного кореня записується як і . Наприклад, квадратне коріння з числа 13 є і . Арифметичний квадратний корінь з нуля дорівнює нулю, тобто . Для негативних чисел a записи ми не надаватимемо сенсу аж до вивчення комплексних чисел. Наприклад, позбавлені сенсу висловлювання та .

За підсумками визначення квадратного кореня доводяться якості квадратного коріння , які найчастіше застосовуються практично.

На закінчення цього пункту зауважимо, що квадратне коріння з числа a є рішеннями виду x 2 =a щодо змінної x .

Кубічний корінь із числа

Визначення кубічного кореняу складі a дається аналогічно визначенню квадратного кореня. Тільки воно виходить з понятті куба числа, а чи не квадрата.

Визначення.

Кубічним коренем у складі aназивається число, куб якого дорівнює a.

Наведемо приклади кубічного коріння . Для цього візьмемо кілька чисел, наприклад, 7 , 0 , −2/3 , і зведемо їх у куб: 7 3 =7 · 7 · 7 = 343, 0 3 = 0 · 0 · 0 = 0 . Тоді, ґрунтуючись на визначенні кубічного кореня, можна стверджувати, що число 7 – це кубічний корінь із 343 , 0 є кубічний корінь із нуля, а −2/3 є кубічним коренем із −8/27 .

Можна показати, що кубічний корінь у складі a , на відміну квадратного кореня, завжди існує, причому як для неотрицательных a , а будь-якого дійсного числа a . Для цього можна використовувати той самий спосіб, який ми згадували при вивченні квадратного кореня.

Більше того, існує тільки єдиний кубічний корінь з даного числа a. Доведемо останнє твердження. Для цього окремо розглянемо три випадки: a – позитивне число, a=0 та a – негативне число.

Легко показати, що з позитивному a кубічний корінь з a може бути ні негативним числом, ні нулем. Справді, нехай b є кубічним коренем з a тоді за визначенням ми можемо записати рівність b 3 =a . Відомо, що це рівність може бути правильним при негативних b і за b=0 , оскільки у випадках b 3 =b·b·b буде негативним числом чи нулем відповідно. Отже, кубічний корінь із позитивного числа a є позитивним числом.

Тепер припустимо, що крім числа b існує ще один кубічний корінь із числа a, позначимо його c. Тоді c 3 = a. Отже, b 3 −c 3 =a−a=0 , але b 3 −c 3 =(b−c)·(b 2 +b·c+c 2)(це формула скороченого множення різницю кубів), звідки (b−c)·(b 2 +b·c+c 2)=0 . Отримана рівність можлива лише коли b−c=0 або b 2 +b·c+c 2 =0 . З першої рівності маємо b=c , а друга рівність немає рішень, оскільки ліва його частина є позитивним числом для будь-яких позитивних чисел b і c як сума трьох позитивних доданків b 2 b c і c 2 . Цим доведено єдиність кубічного кореня з позитивного числа a.

При a=0 кубічним коренем у складі a є лише число нуль. Дійсно, якщо припустити, що існує число b, яке є відмінним від нуля кубічним коренем з нуля, то має виконуватись рівність b3=0, яка можлива лише при b=0.

Для негативних a можна навести міркування, аналогічні випадку позитивних a . По-перше, показуємо, що кубічний корінь з негативного числа не може дорівнювати ні позитивному числу, ні нулю. По-друге, припускаємо, що існує другий кубічний корінь із негативного числа і показуємо, що він обов'язково співпадатиме з першим.

Отже, завжди існує кубічний корінь з будь-якого даного дійсного числа a, причому єдиний.

Дамо визначення арифметичного кубічного кореня.

Визначення.

Арифметичним кубічним коренем з негативної кількості aназивається невід'ємне число, куб якого дорівнює a.

Арифметичний кубічний корінь з невід'ємного числа a позначається як , знак називається знаком арифметичного кубічного кореня, число 3 у цьому записі називається показником кореня. Число під знаком кореня – це підкорене число, вираз під знаком кореня – це підкорене вираз.

Хоча арифметичний кубічний корінь визначається лише для невід'ємних чисел a, але зручно також використовувати записи, в яких під знаком арифметичного кубічного кореня знаходяться негативні числа. Розуміти їх будемо так: , де -ой ступеня у складі a – це число, n -я ступінь якого дорівнює a .

З даного визначенняВідомо, що корінь першого ступеня у складі a є саме число a , оскільки щодо ступеня з натуральним показникомми прийняли a 1 = a.

Вище ми розглянули окремі випадки кореня n-ого ступеня при n=2 і n=3 – квадратний корінь та кубічний корінь. Тобто квадратний корінь – це корінь другого ступеня, а кубічний корінь – корінь третього ступеня. Для вивчення коренів n-ого ступеня при n=4, 5, 6, … їх зручно розділити на дві групи: перша група – корені парних ступенів (тобто, при n=4, 6, 8, …), друга група – коріння непарних ступенів (тобто, при n=5, 7, 9, …). Це з тим, що коріння парних ступенів аналогічні квадратному кореню, а коріння непарних ступенів – кубическому. Розберемося з ними по черзі.

Почнемо з коріння, ступенями яких є парні числа 4, 6, 8, … Як ми вже сказали, вони аналогічні квадратному кореню з числа a . Тобто, корінь будь-якого парного ступеня у складі a існує лише для неотрицательного a . Причому, якщо a=0 , то корінь a єдиний і дорівнює нулю, а якщо a>0 , то існує два корені парного ступеня з числа a , причому вони є протилежними числами.

Обґрунтуємо останнє твердження. Нехай b – корінь парного ступеня (позначимо її як 2·m, де m – деяке натуральне число) у складі a . Припустимо, що є число c – ще один корінь ступеня 2·m у складі a . Тоді b 2m −c 2m =a−a=0 . Але ми знаємо виду b 2·m −c 2·m = (b−c)·(b+c)· (b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2)тоді (b−c)·(b+c)· (b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2)=0. З цієї рівності випливає, що b-c=0 , або b+c=0 , або b 2·m−2 +b 2·m−4 ·c 2 +b 2·m−6 ·c 4 +…+c 2·m−2 =0. Перші дві рівності означають, що числа b і c рівні, або b і c – протилежні. А остання рівність справедлива лише за b=c=0 , оскільки у його лівої частини перебуває вираз, яке неотрицательно при будь-яких b і як сума неотрицательных чисел.

Що стосується коренів n-ого ступеня при непарних n, то вони аналогічні кубічному кореню. Тобто, корінь будь-якої непарної міри з числа a існує для будь-якого дійсного числа a, причому для даного числа a є єдиним.

Єдиність кореня непарного ступеня 2·m+1 у складі a доводиться за аналогією з доказом єдиності кубічного кореня з a . Тільки тут замість рівності a 3 −b 3 =(a−b)·(a 2 +a·b+c 2)використовується рівність виду b 2·m+1 −c 2·m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m). Вираз в останній дужці можна переписати як b 2·m +c 2·m +b·c·(b 2·m−2 +c 2·m−2 + b·c·(b 2·m−4 +c 2·m−4 +b·c·(…+(b 2 +c 2 +b·c)))). Наприклад, при m=2 маємо b 5 −c 5 =(b−c)·(b 4 +b 3 ·c+b 2 ·c 2 +b·c 3 +c 4)= (b−c)·(b 4 +c 4 +b·c·(b 2 +c 2 +b·c)). Коли a та b обидва позитивні або обидва негативні їх твір є позитивним числом, тоді вираз b 2 +c 2 +b·c , що знаходиться в дужках найвищого ступеня вкладеності, є позитивним як сума позитивних чисел. Тепер, просуваючись послідовно до виразів у дужках попередніх ступенів вкладеності, переконуємось, що вони також позитивні як суми позитивних чисел. У результаті отримуємо, що рівність b 2·m+1 −c 2·m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)=0можливо тільки тоді, коли b−c=0 , тобто коли число дорівнює числу c .

Настав час розібратися з позначеннями коренів n-ого ступеня. Для цього дається визначення арифметичного кореня n-ого ступеня.

Визначення.

Арифметичним корінням n-ого ступеня з невід'ємного числа aназивається неотрицательное число, n -я ступінь якого дорівнює a.

Арифметичний корінь n-го ступеня з невід'ємного числа a позначається як . Число a називають підкореним числом, а число n – показник кореня. Наприклад розглянемо запис , тут підкореним числом є 125,36 , а показник кореня дорівнює 5 .

Зауважимо, що з n=2 ми маємо справу з квадратним коренем у складі, у разі показник кореня прийнято не записувати, тобто, записи і означають те саме число.

Незважаючи на те, що визначення арифметичного квадратного кореня n-ого ступеня, а також його позначення введені для невід'ємних підкорених чисел, ми з метою зручності для непарних показників кореня та негативних підкорених чисел використовуватимемо записи виду, які розумітимемо як . Наприклад, 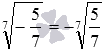і .

Корінням же парного ступеня з негативними підкореними числами ми не надаватимемо жодного сенсу (до початку вивчення комплексних чисел). Наприклад, вирази та

Гусєв В.А., Мордкович А.Г. Математика (посібник для вступників до технікумів).

• Корінь неспроможна дорівнювати непозитивному числу.

• Важливо розуміти, що квадратний корінь – це інший запис ступеня ½:

Наприклад:

• Величина кореня не зміниться, якщо його показник збільшити в n разів і одночасно звести підкорене значення ступінь n:

• Величина кореня не зміниться, якщо показник ступеня зменшити в n раз і одночасно витягти корінь n-го ступеня з підкореного значення:

• Корінь від приватного дорівнює приватному від розподілу кореня з поділеного на корінь з дільника (показники коренів повинні бути однаковими):

• Щоб звести корінь у ступінь, достатньо звести в цей ступінь підкорене значення:

Назад, щоб витягти корінь із ступеня, достатньо звести в цей ступінь корінь із основи ступеня:

• Корінь із твору кількох співмножників дорівнює творукоріння того ж ступеня з цих співмножників (теж важливе властивість коріння):

Назад, твір коренів одного й того ж ступеня дорівнює кореню того ж ступеня з твору підкорених значень:

Квадратний корінь, як елементарна функція.

Це елементарна функція та окремий випадокстепеневої функції при . Арифметичний квадратний корінь є гладким при , а в нулі він безперервний праворуч, але не диференціюється (відмінне свійство коренів).

Як функція комплексний змінний корінь – двозначна функція, у якої листи сходяться на нулі.

Властивість кореня як функції.

На "en":["HdXjyHnNwKI","_R0NEXjoqvE","CRl1vbsEzfE","HdXjyHnNwKI","eU0Ls3HXGSM"],"de":["YsdvCMSwNIE","YsdvCmw ],"es":["Ua9_FIARcs0","2OMyIgVOJA8","wwJbyRkNBDI","jLABnDNi7KI","Ua9_FIARcs0","lsP_XKF-q0g","rEA8GFKLIGY","MPmNWyyu NBDA-T0DA6w"],"pt":["KQ4Nx58MzUM","uNFy0kkolHw","zQAEoNT0H4w"],"fr":["lm_yqzUYGe4","eU0Ls3HXGSM"],"bg":["Dq w","di17cqmHH8c"],"cs":["yDFfyEhpATg"],"ro":["rmkZhdl4Sj4","rmkZhdl4Sj4","ZZlbxSMk7jU"],"lt":["zl3P_D6uzqM, WUJmagS13Sw","blf7jNq7maI"])