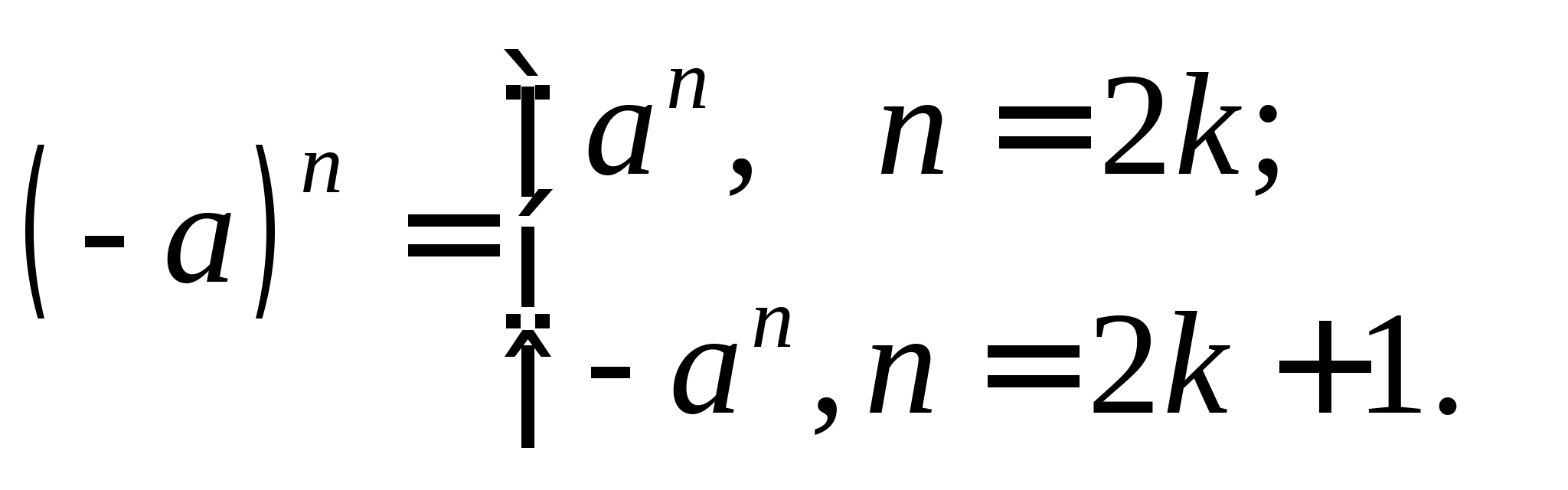Ступінь числа із натуральним показником. Ступінь із цілим показником
Нижченаведена формула буде визначенням ступеня з натуральним показником(a - основа ступеня і множник, що повторюється, а n - показник ступеня, який показує скільки разів повторюється множник):
Даний вираз означає, що ступінь числа a з натуральним показником n є добутком n співмножників, при тому що кожен з множників дорівнює a .
17^5=17 \cdot 17 \cdot 17 \cdot 17 \cdot 17=1\,419\,857
17 - підстава ступеня,
5 - показник ступеня,
1419857 - значення ступеня.
Ступінь з нульовим показником дорівнює 1 за умови, що a \neq 0 :
a^0=1.
Наприклад: 2^0=1
Коли потрібно записати велике число, зазвичай використовують ступінь числа 10 .
Наприклад, один із найдавніших динозаврів на Землі жив близько 280 млн. років тому. Його вік записується так: 2,8 \cdot 10^8 .
Кожне число більше 10 можна записати як a \cdot 10^n , за умови, що 1< a < 10 и n является положительным целым числом . Такую запись называют стандартним видом числа.
Приклади таких чисел: 6978 = 6,978 \ cdot 10 ^ 3, 569000 = 5,69 \ cdot 10 ^ 5.
Можна говорити як і «a в n-му ступені», так і «n-а ступінь числа a» і «a у ступені n».
4^5 — «чотири в ступені 5» або «4 в п'ятому ступені» або також можна сказати «п'ятий рівень числа 4»
У даному прикладі 4 - основа ступеня, 5 - показник ступеня.
Наведемо тепер приклад із дробами та негативними числами. Для уникнення плутанини прийнято записувати підстави, відмінні від натуральних чисел, у дужках:
(7,38)^2 , \left(\frac 12 \right)^7, (-1) ^ 4 та ін.
Зауважте також різницю:
(-5)^6 - означає ступінь негативного числа−5 з натуральним показником 6.
5^6 - відповідає числу протилежному 5^6.
Властивості ступенів із натуральним показником
Основна властивість ступеня
a^n \cdot a^k = a^(n+k)
Підстава залишається незмінною, а складаються показники ступенів.
Наприклад: 2^3 \cdot 2^2 = 2^(3+2)=2^5
Властивість приватного ступеня з однаковими підставами
a^n: a^k=a^(n-k), якщо n > k.
Показники ступеня віднімаються, а підстава залишається незмінною.
Дане обмеження n > k вводиться для того, щоб не виходити за межі натуральних показників ступеня. Справді, при n > k показник ступеня a^(n-k) буде натуральним числом, інакше він буде негативним числом (k< n ), либо нулем (k-n ).
Наприклад: 2^3: 2^2 = 2^(3-2)=2^1
Властивість зведення ступеня до ступеня
(a^n)^k=a^(nk)
Підстава залишається незмінною, перемножуються лише показники ступенів.
Наприклад: (2^3)^6 = 2^(3 \cdot 6)=2^(18)
Властивість зведення у ступінь твору
У міру n зводиться кожен множник.
a^n \cdot b^n = (ab)^n
Наприклад: 2^3 \cdot 3^3 = (2 \cdot 3)^3=6^3
Властивість зведення в міру дробу
\frac(a^n)(b^n)=\left(\frac(a)(b) \right) ^n, b \neq 0
У ступінь зводиться і чисельник та знаменник дробу. \left(\frac(2)(5) \right)^3=\frac(2^3)(5^3)=\frac(8)(125)
I.твір nзмножувачів, кожен з яких дорівнює аназивається n-й ступенем числа аі позначається аn.
приклади. Записати твір як ступеня.
1) мммм; 2) aaabb; 3) 5 · 5 · 5 · 5 · ccc; 4) ppkk+ppk-ppkkk.
Рішення.
1) mmmm=m 4, оскільки, за визначенням ступеня, твір чотирьох співмножників, кожен з яких дорівнює m, буде четвертим ступенем числа m.
2) aaabb = a 3 b 2; 3) 5·5·5·5·ccc=5 4 c 3 ; 4) ppkk+pppk-ppkkk=p 2 k 2 +p 3 k-p 2 k 3 .
ІІ.Дія, з якого перебуває твір кількох рівних співмножників, називається зведенням у ступінь. Число, яке зводиться у ступінь, називається основою ступеня. Число, яке показує, на яку міру зводиться основа, називається показником ступеня. Так, аn- Ступінь, а- Основа ступеня, n- показник ступеня. Наприклад:
2 3 — це ступінь. Число 2 - Основа ступеня, показник ступеня дорівнює 3 . Значення ступеня 2 3 одно 8, так як 2 3 = 2 · 2 · 2 = 8.
приклади. Написати такі вирази без показника ступеня.
5) 4 3; 6) a 3 b 2 c 3; 7) a 3 -b 3; 8) 2a4 +3b2.
Рішення.
5) 4 3 = 4·4·4 ; 6) a 3 b 2 c 3 = aaabbccc; 7) a 3 -b 3 = aaa-bbb; 8) 2a 4 +3b 2 = 2aaaa+3bb.
ІІІ.а 0 = 1 Будь-яке число (крім нуля) в нульового ступеняодно одиниці. Наприклад, 250 =1.
IV.а 1 = аБудь-яке число в першому ступені дорівнює самому собі.
V. a m∙ a n= a m + n При множенні ступенів однаковими підставамипідставу залишають тим самим, а показники складають.
приклади. Спростити:
9) a · a 3 · a 7; 10) b 0 +b 2 · b 3; 11) c 2 · c 0 · c · c 4 .
Рішення.
9) a·a 3 ·a 7=a 1+3+7 =a 11; 10) b 0 +b 2 · b 3 = 1+b 2+3 =1+b 5;
11) c 2 · c 0 · c · c 4 = 1·c 2 ·c·c 4 =c 2+1+4 =c 7 .
VI. a m: a n= a m - nПри розподілі ступенів з однаковими основами основу залишають колишнім, та якщо з показника ступеня поділеного віднімають показник ступеня дільника.
приклади. Спростити:
12) a 8: a 3; 13) m 11: m 4 ; 14) 5 6:5 4 .
12) a 8:a 3=a 8-3 =a 5; 13) m 11:m 4= m 11-4 = m 7; 14 ) 5 6:5 4 =5 2 =5 · 5 = 25.
VII. (a m) n= a mn При зведенні ступеня ступінь основу залишають колишнім, а показники перемножують.
приклади. Спростити:
15) (a 3) 4; 16) (з 5) 2.
15) (a 3) 4= a 3 · 4 = a 12; 16) (c 5) 2= c 5 · 2 = c 10 .
Зверніть увагу, що, оскільки від перестановки множників твір не змінюється, то:
15) (a 3) 4 = (a 4) 3; 16) (c 5) 2 = (c 2) 5 .
VI II. (a∙b) n =a n ∙b n При зведенні твору на ступінь зводять у цей ступінь кожен із множників.
основна ціль
Ознайомити учнів із властивостями ступенів із натуральними показниками та навчити виконувати дії зі ступенями.
Тема " Ступінь та її властивості "включає три питання:
- Визначення ступеня із натуральним показником.
- Розмноження та розподіл ступенів.
- Зведення у ступінь твору та ступеня.
Контрольні питання
- Сформулюйте визначення ступеня з натуральним показником 1. Наведіть приклад.
- Сформулюйте визначення ступеня із показником 1. Наведіть приклад.
- Яким є порядок виконання дій при обчисленні значення виразу, що містить ступеня?
- Сформулюйте основну властивість ступеня. Наведіть приклад.
- Сформулюйте правило множення ступенів із однаковими основами. Наведіть приклад.
- Сформулюйте правило розподілу ступенів з однаковими основами. Наведіть приклад.
- Сформулюйте правило зведення ступінь твору. Наведіть приклад. Доведіть тотожність (ab) n = a n b n .
- Сформулюйте правило зведення ступеня до ступеня. Наведіть приклад. Доведіть тотожність (а m) n = m n .
Визначення ступеня.
Ступенем числа aз натуральним показником n, Великим 1, називається добуток n множників, кожен з яких дорівнює а. Ступенем числа аз показником 1 називається саме число а.
Ступінь з основою ата показником nзаписується так: а n. Читається “ ау ступені n”; У n- я ступінь числа а ”.
За визначенням ступеня:
а 4 = а а а а
. . . . . . . . . . . .
Знаходження значення ступеня називають зведенням у ступінь .
1. Приклади зведення у ступінь:
3 3 = 3 3 3 = 27
0 4 = 0 0 0 0 = 0
(-5) 3 = (-5) (-5) (-5) = -125
25 ; 0,09 ;
25 = 5 2 ; 0,09 = (0,3) 2 ; .
27 ; 0,001 ; 8 .
27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .
4. Знайти значення виразів:
а) 3 10 3 = 3 10 10 10 = 3 1000 = 3000
б) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7
Варіант 1
а) 0,3 0,3 0,3
в) b b b b b b b b
г) (-х) (-х) (-х) (-х)
д) (ab) (ab) (ab)
2. Подайте у вигляді квадрата числа:
3. Подайте у вигляді куба числа:
4. Знайти значення виразів:
в) -1 4 + (-2) 3
г) -4 3 + (-3) 2
д) 100 - 5 2 4
Розмноження ступенів.
Для будь-якого числа а та довільних чисел m і n виконується:
a m a n = a m + n.
Доведення:
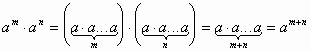
Правило : При множенні степенів з однаковими основами основи залишають колишнім, а показники степенів складають.
a m a n a k = a m + n a k = a (m + n) + k = a m + n + k
а) х 5 х 4 = х 5 + 4 = х 9
б) y y 6 = y 1 y 6 = y 1 + 6 = y 7
в) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11
г) 3 4 9 = 3 4 3 2 = 3 6
д) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5
а) 2 3 2 = 2 4 = 16
б) 3 2 3 5 = 3 7 = 2187
Варіант 1
1. Подати у вигляді ступеня:
а) х 3 х 4 е) х 2 х 3 х 4
б) а 6 а 2 ж) 3 3 9
в) у 4 у з) 7 4 49
г) а а 8 і) 16 2 7
д) 2 3 2 4 к) 0,3 3 0,09
2. Подати у вигляді ступеня та знайти значення за таблицею:
а) 2 2 2 3 в) 8 2 5
б) 3 4 3 2 г) 27 243
Розподіл ступенів.
Для будь-якого числа а0 та довільних натуральних чисел m і n, таких, що m>n виконується:
a m: a n = a m - n
Доведення:
a m - n a n = a (m - n) + n = a m - n + n = a m
за визначенням приватного:
a m: a n = a m - n.
Правило: При розподілі ступенів з однаковими основами основу залишають колишнім, та якщо з показника ступеня поділеного віднімають показник ступеня дільника.
Визначення: Ступінь числа а, не рівного нулю, з нульовим показником дорівнює одиниці:
т.к. а n: a n = 1 при а0.
а) х 4: х 2 = х 4 - 2 = х 2
б) у 8: у 3 = у 8 - 3 = у 5
в) а 7: а = а 7: а 1 = а 7 - 1 = а 6
г) з 5: з 0 = з 5: 1 = з 5
а) 5 7:5 5 = 5 2 = 25
б) 10 20:10 17 = 10 3 = 1000
в)
г)
д)
Варіант 1
1. Подайте у вигляді ступеня приватне:
2. Знайдіть значення виразів:
Зведення у ступінь твору.
Для будь-яких а та b і довільного натурального числа n:
(ab) n = a n b n
Доведення:
За визначенням ступеня
(ab) n = ![]()
Згрупувавши окремо множники а та множники b, отримаємо:
![]() =
= ![]()
Доведена властивість ступеня твору поширюється на ступінь твору трьох та більше множників.
Наприклад:
(a b c) n = a n b n c n;
(a b c d) n = a n b n c n d n .
Правило: При зведенні у ступінь твору зводять у цей ступінь кожен множник і результат перемножують
1. Звести до ступеня:
а) (a b) 4 = a 4 b 4
б) (2 х у) 3 = 2 3 х 3 у 3 = 8 х 3 у 3
в) (3 а) 4 = 3 4 а 4 = 81 а 4
г) (-5 у) 3 = (-5) 3 у 3 = -125 у 3
д) (-0,2 х у) 2 = (-0,2) 2 х 2 у 2 = 0,04 х 2 у 2
е) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4
2. Знайти значення виразу:
а) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000
б) (3 5 20) 2 = 3 2 100 2 = 9 10000 = 90000
в) 2 4 5 4 = (2 5) 4 = 10 4 = 10000
г) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1
д)
Варіант 1
1. Звести до ступеня:
б) (2 а з) 4
д) (-0,1 х у) 3
2. Знайти значення виразу:
б) (5 7 20) 2
Зведення у ступінь ступеня.
Для будь-якого числа а та довільних натуральних чисел m і n:
(а m) n = а m n
Доведення:
За визначенням ступеня
(а m) n = ![]()
Правило: При зведенні ступеня в ступінь основу залишають тим самим, а показники перемножують.
1. Звести до ступеня:
(а 3) 2 = а 6 (х 5) 4 = х 20
(у 5) 2 = у 10 (b 3) 3 = b 9
2. Спростіть вирази:
а) а 3 (а 2) 5 = а 3 а 10 = а 13
б) (b 3) 2 b 7 = b 6 b 7 = b 13
в) (х 3) 2 (х 2) 4 = х 6 х 8 = х 14
г) (у 7) 3 = (у 8) 3 = 24
а)
б)
Варіант 1
1. Звести до ступеня:
а) (а 4) 2 б) (х 4) 5
в) (у 3) 2 г) (b 4) 4
2. Спростіть вирази:
а) а 4 (а 3) 2
б) (b 4) 3 b 5+
в) (х 2) 4 (х 4) 3
г) (у 9) 2
3. Знайдіть значення виразів:
додаток
Визначення ступеня.
Варіант 2
1ю Запишіть твір у вигляді:
а) 04 04 04
в) а а а а а а а а
г) (-у) (-у) (-у) (-у)
д) (bс) (bс) (bс)
2. Подайте у вигляді квадрата числа:
3. Подайте у вигляді куба числа:
4. Знайти значення виразів:
в) -1 3 + (-2) 4
г) -6 2 + (-3) 2
д) 4 5 2 – 100
Варіант 3
1. Запишіть твір як:
а) 0,5 0,5 0,5
в) с с с с с с с
г) (-х) (-х) (-х) (-х)
д) (ab) (ab) (ab)
2. Подайте у вигляді квадрата числа: 100; 0,49; .
3. Подайте у вигляді куба числа:
4. Знайти значення виразів:
в) -1 5 + (-3) 2
г) -5 3 + (-4) 2
д) 5 4 2 - 100
Варіант 4
1. Запишіть твір як:
а) 0,7 0,7 0,7
в) х х х х х х
г) (-а) (-а) (-а)
д) (bс) (bс) (bс) (bc)
2. Подайте у вигляді квадрата числа:
3. Подайте у вигляді куба числа:
4. Знайти значення виразів:
в) -1 4 + (-3) 3
г) -3 4 + (-5) 2
д) 100 - 3 2 5
Розмноження ступенів.
Варіант 2
1. Подати у вигляді ступеня:
а) х 4 х 5 е) х 3 х 4 х 5
б) а 7 а 3 ж) 2 3 4
в) у 5 у з) 4 3 16
г) а а 7 і) 4 2 5
д) 2 2 2 5 к) 0,2 3 0,04
2. Подати у вигляді ступеня та знайти значення за таблицею:
а) 3 2 3 3 в) 16 2 3
б) 2 4 2 5 г) 9 81
Варіант 3
1. Подати у вигляді ступеня:
а) а 3 а 5 е) у 2 у 4 у 6
б) х 4 х 7 ж) 3 5 9
в) b 6 b з) 5 3 25
г) у 8 і) 49 7 4
д) 2 3 2 6 к) 0,3 4 0,27
2. Подати у вигляді ступеня та знайти значення за таблицею:
а) 3 3 3 4 в) 27 3 4
б) 2 4 2 6 г) 16 64
Варіант 4
1. Подати у вигляді ступеня:
а) а 6 а 2 е) х 4 х х 6
б) х 7 х 8 ж) 3 4 27
в) у 6 у з) 4 3 16
г) х х 10 і) 36 6 3
д) 2 4 2 5 к) 0,2 2 0,008
2. Подати у вигляді ступеня та знайти значення за таблицею:
а) 2 6 2 3 в) 64 2 4
б) 3 5 3 2 г) 81 27
Розподіл ступенів.
Варіант 2
1. Подайте у вигляді ступеня приватне:
2. Знайдіть значення виразів.
РОЗДІЛ 2. СТУПЕНІ
2.1. Ступінь із натуральним показником
Визначення. Ступенем числа а з натуральним показникомn(n>1) називається твірnзмножувачів, кожен з яких дорівнює а. , а 1 =а.
Властивості ступенів із натуральним показником:
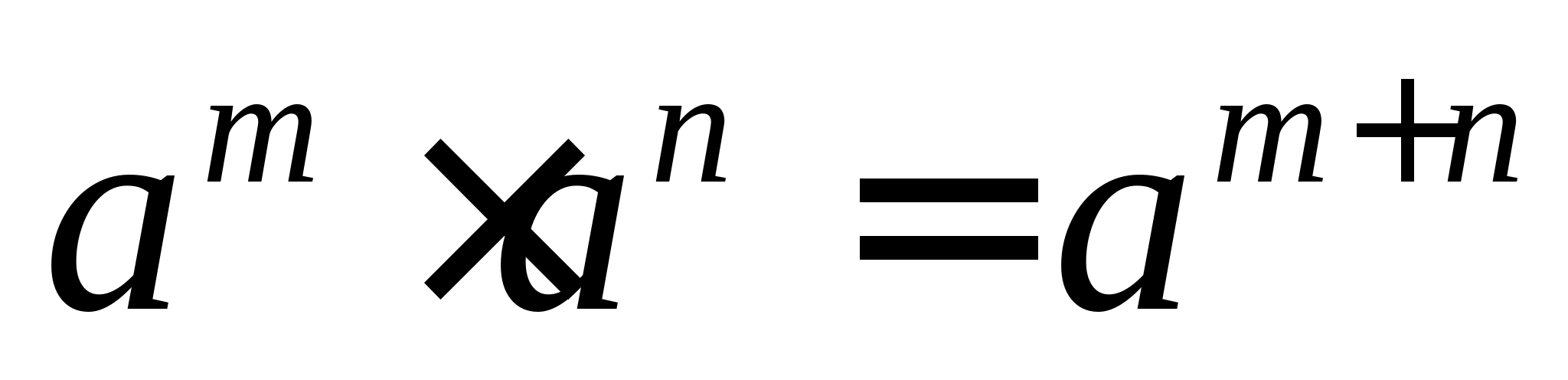 | 4. |
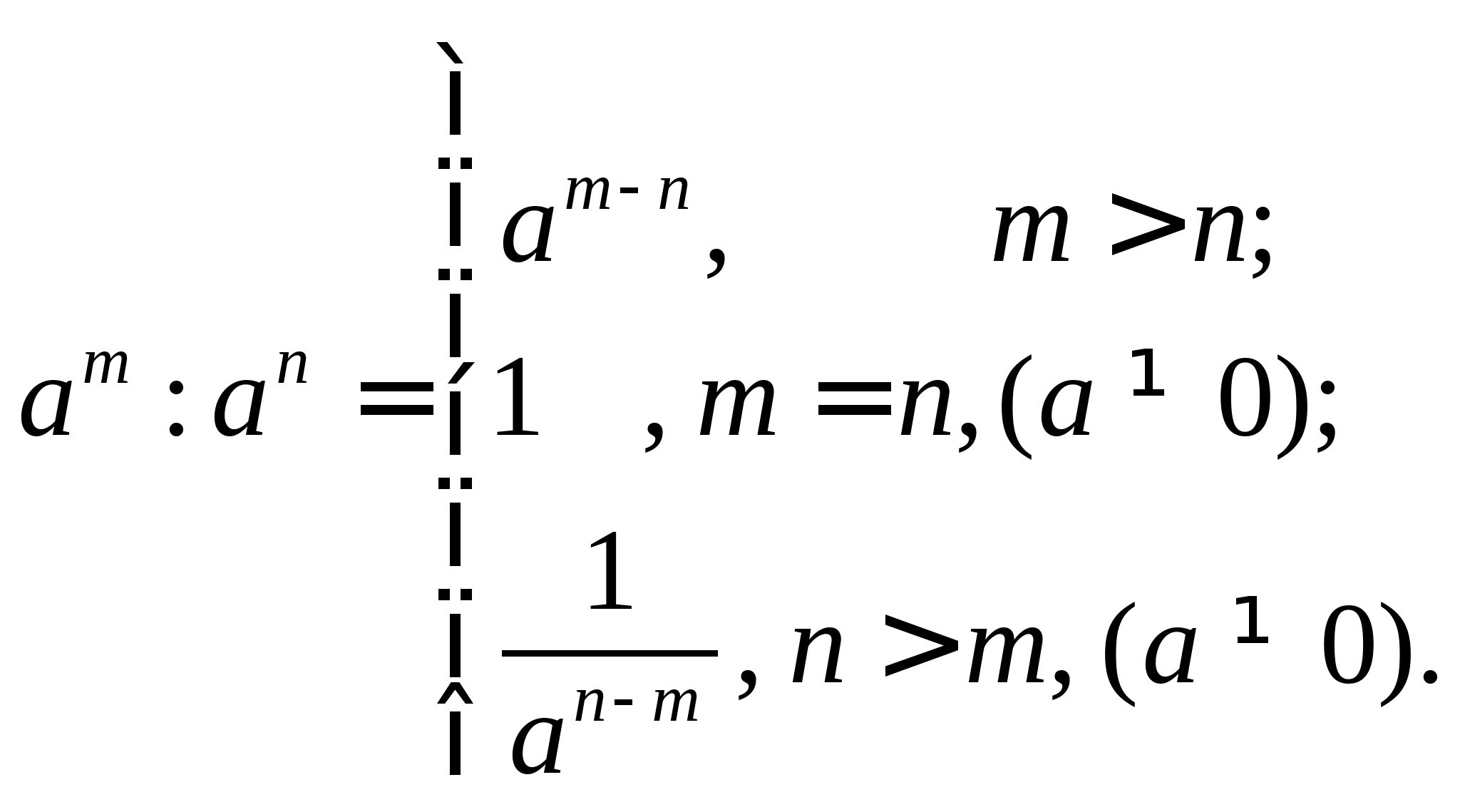 | 5. |
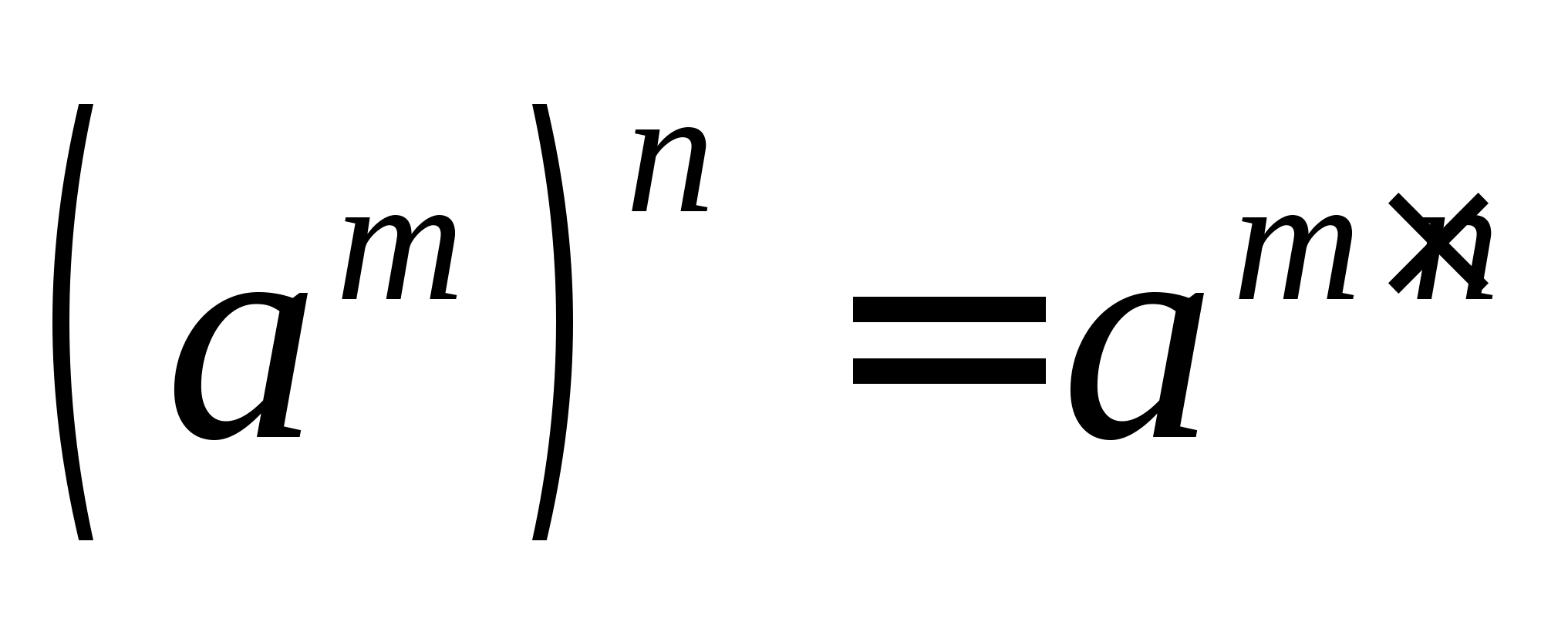 | 6. |
Приклад 1. Обчислити: 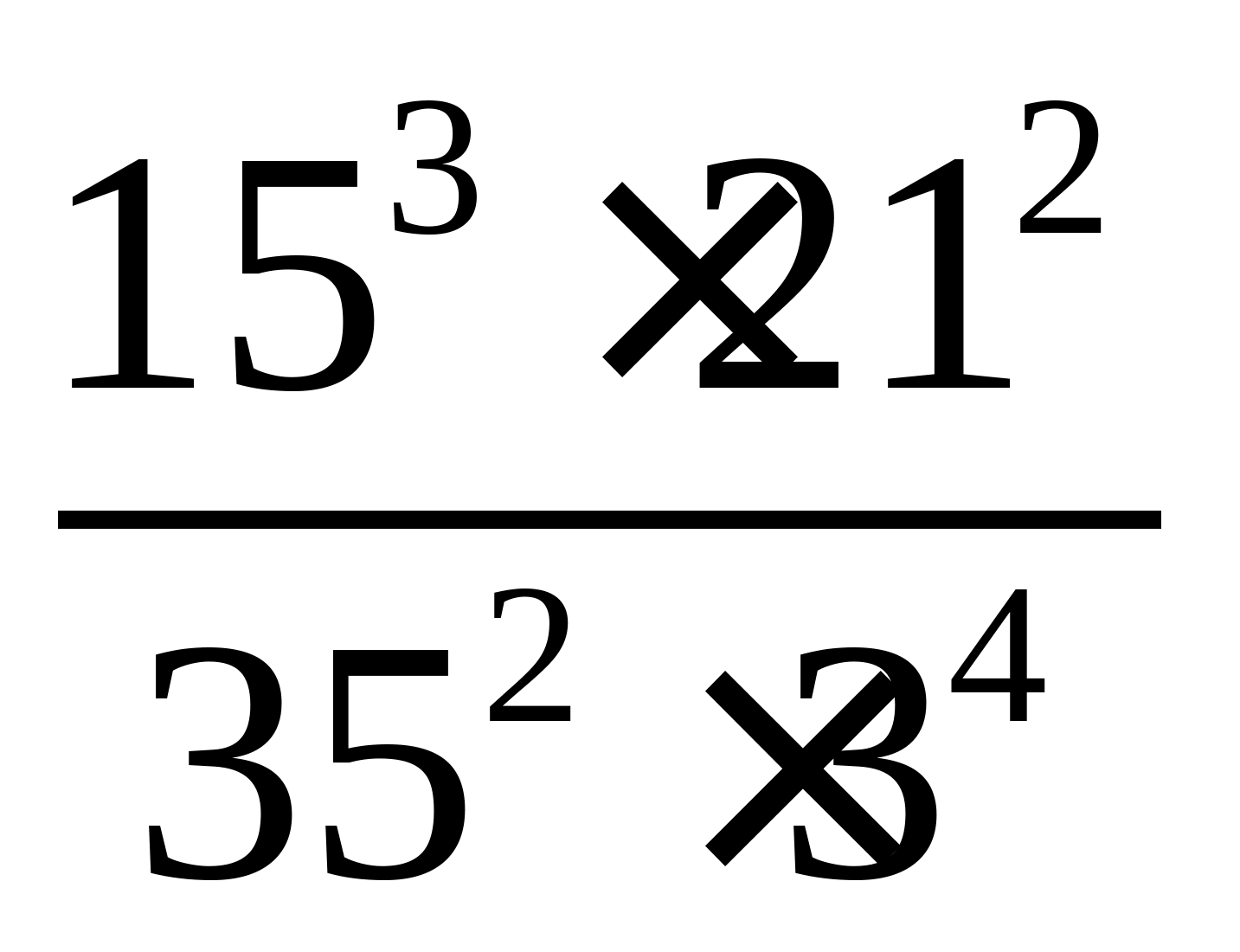 .
.
Рішення.
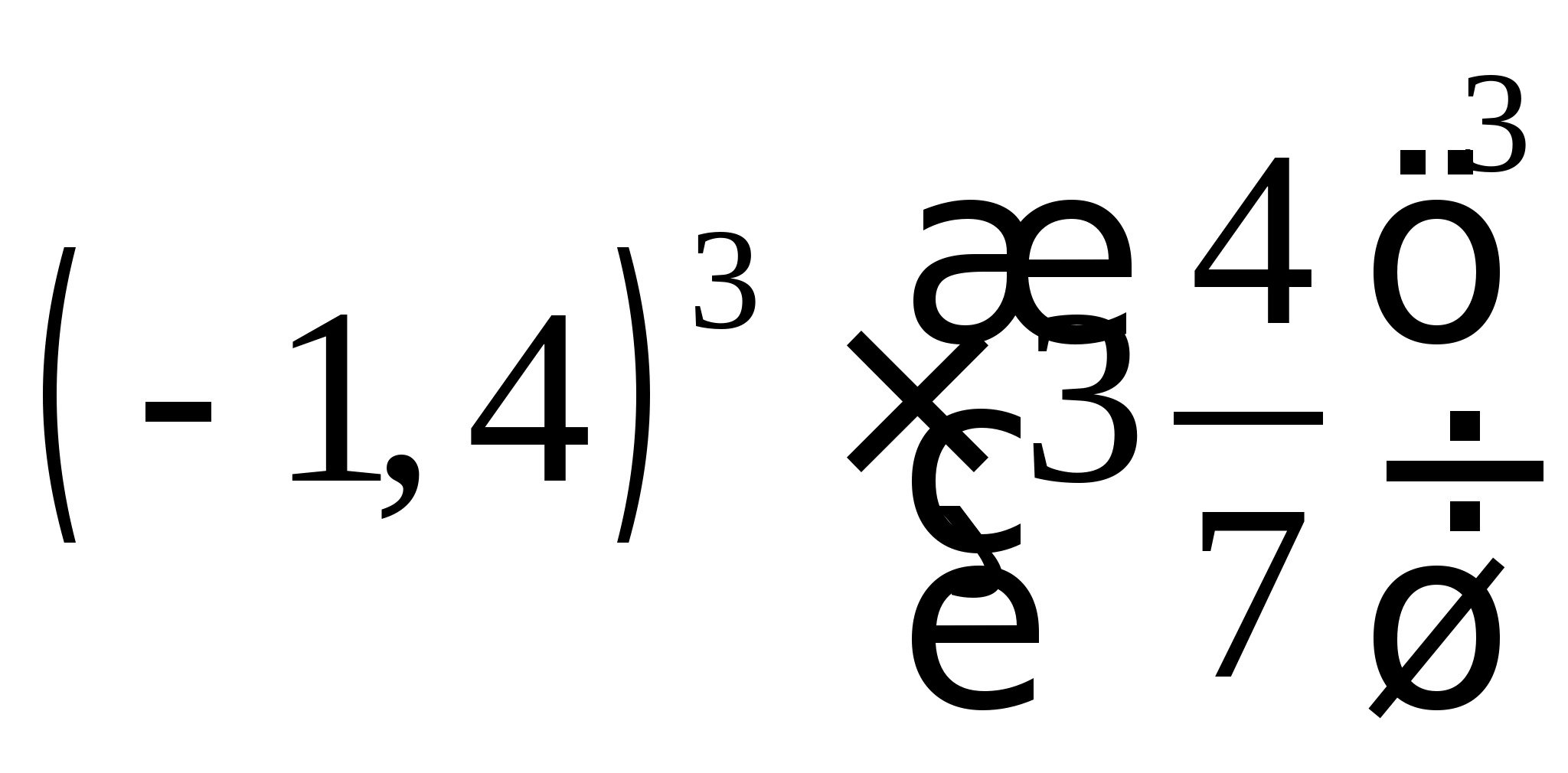 .
.
Рішення.
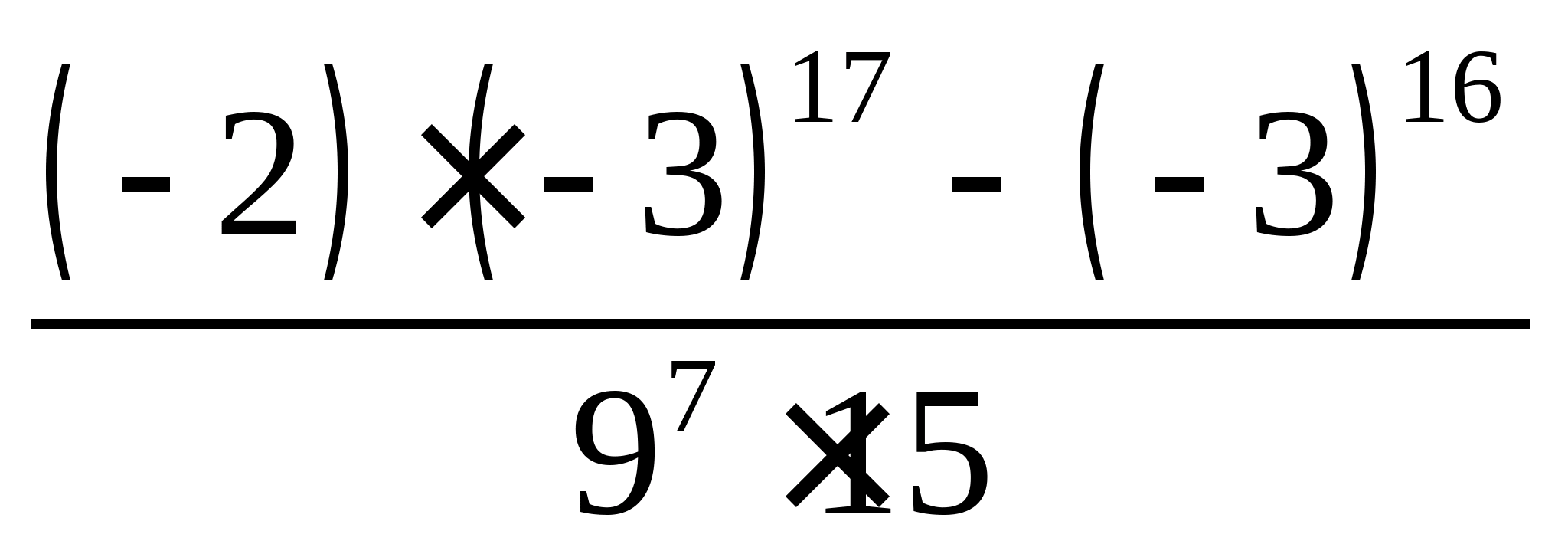 .
.
Рішення.
Приклад 4. Розташувати у порядку зростання такі числа:
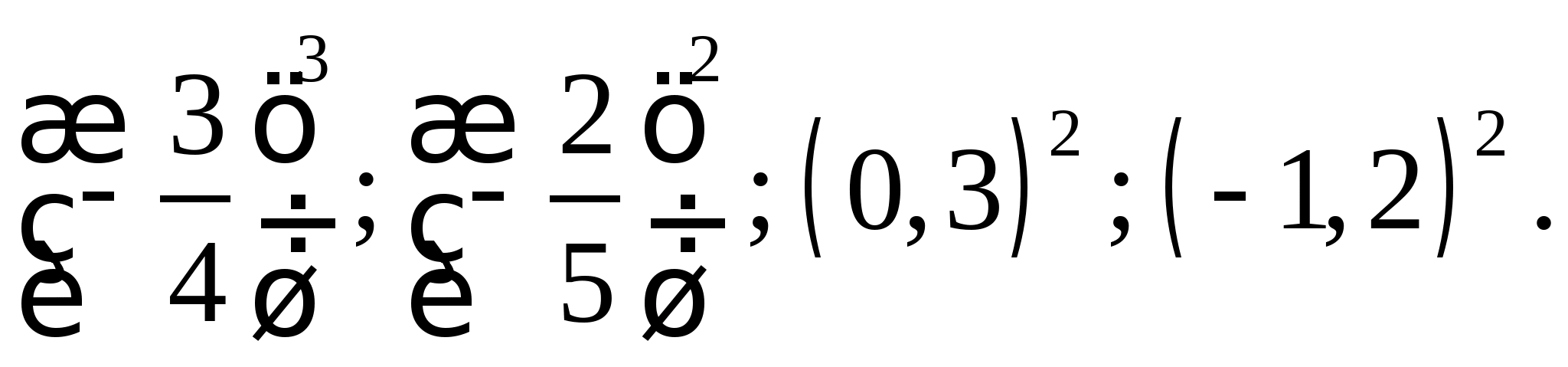
Рішення.
Звідси: 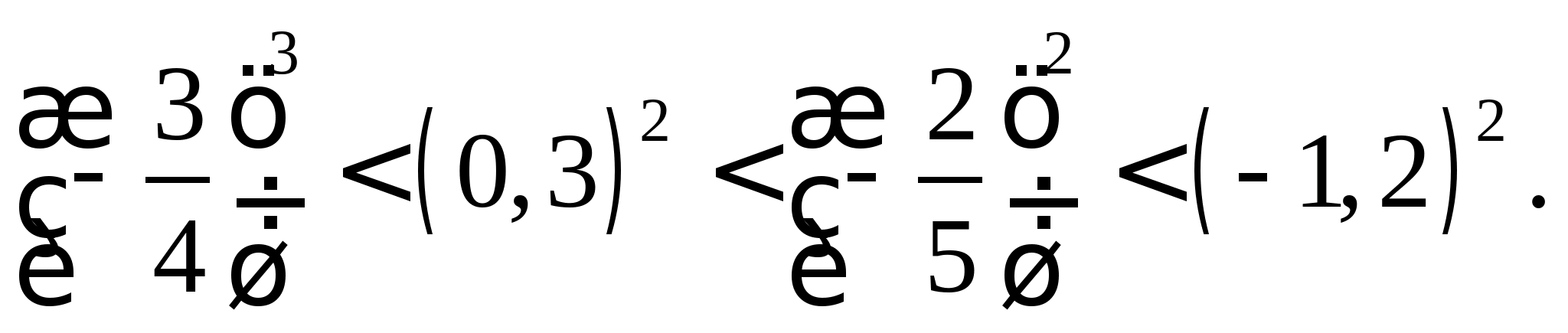
2.2. Ступінь із цілим показником
Узагальнюючи поняття ступеня з натуральним показником, введемо ступеня з нульовим та цілим негативним показниками.
Визначення: Якщо a≠0, то a 0 =1 . Вираз 0 0 не має сенсу.
Визначення: Якщо a≠0
, і n- Натуральне, то 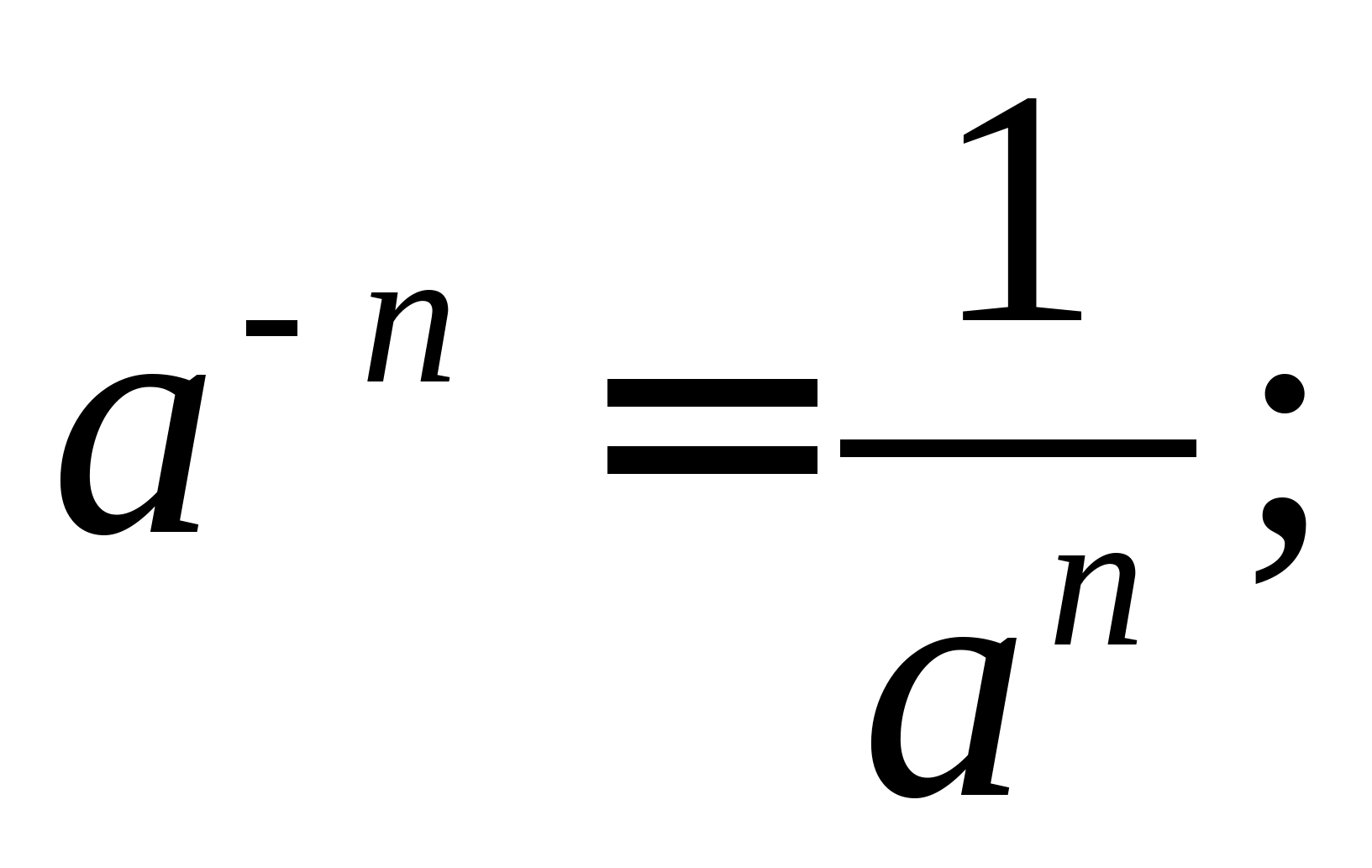
Вираз 0 - nне має сенсу.
Властивість 2 ступеня з натуральним показником можна тепер, використовуючи поняття ступеня з нульовим та цілим негативним показником, записати у вигляді: 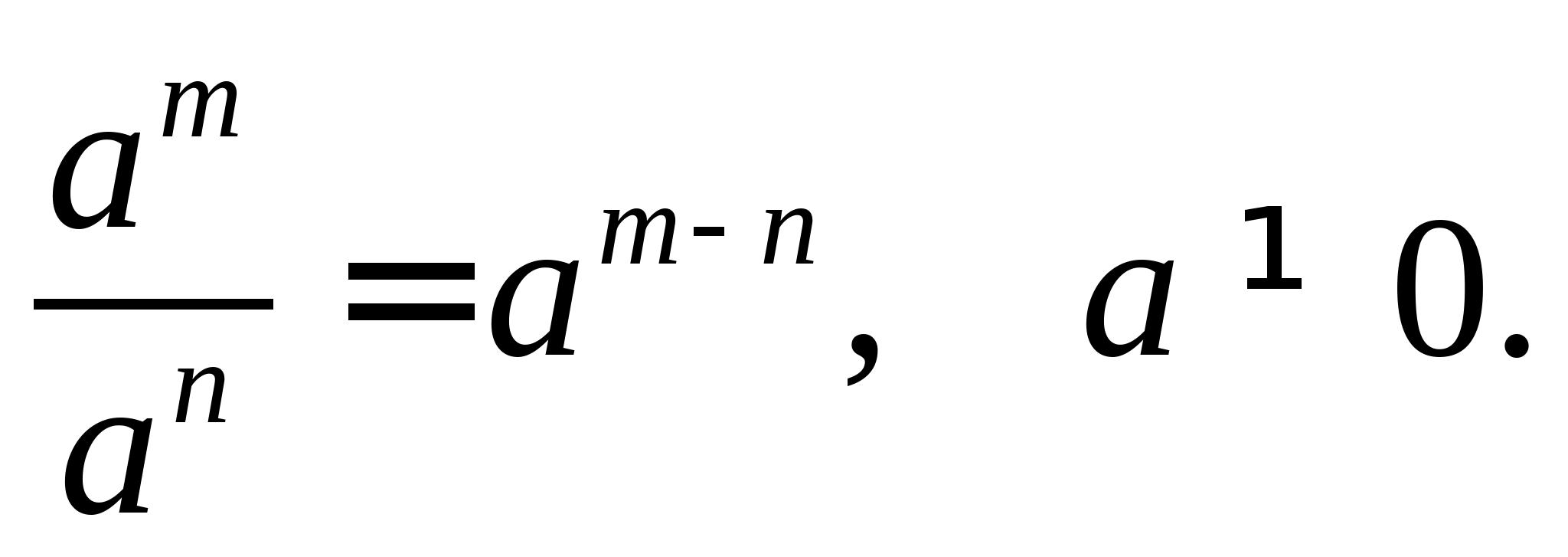 Інші властивості мають той самий запис.
Інші властивості мають той самий запис.
Приклад 1. Обчислити: 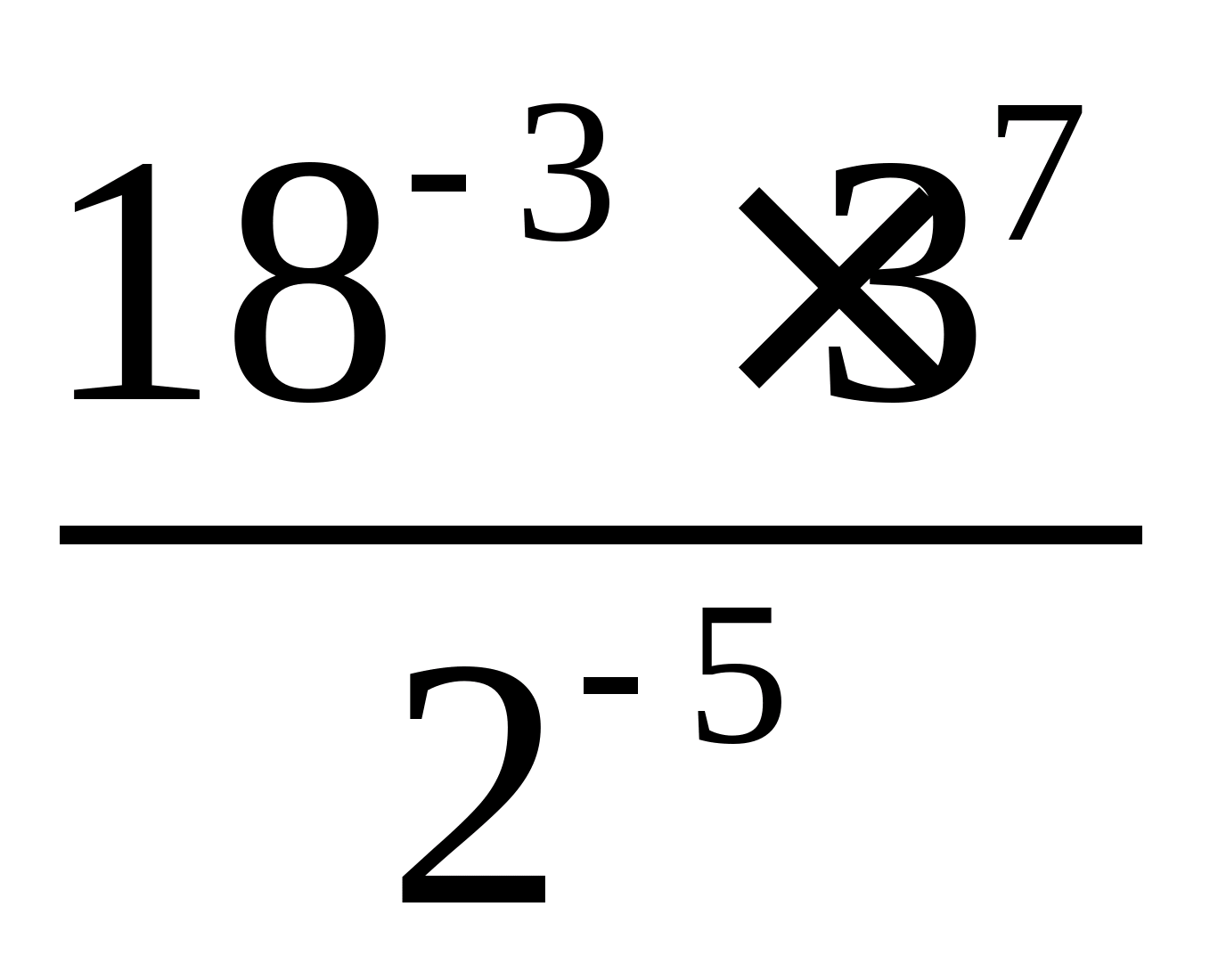 ;
;
Рішення. 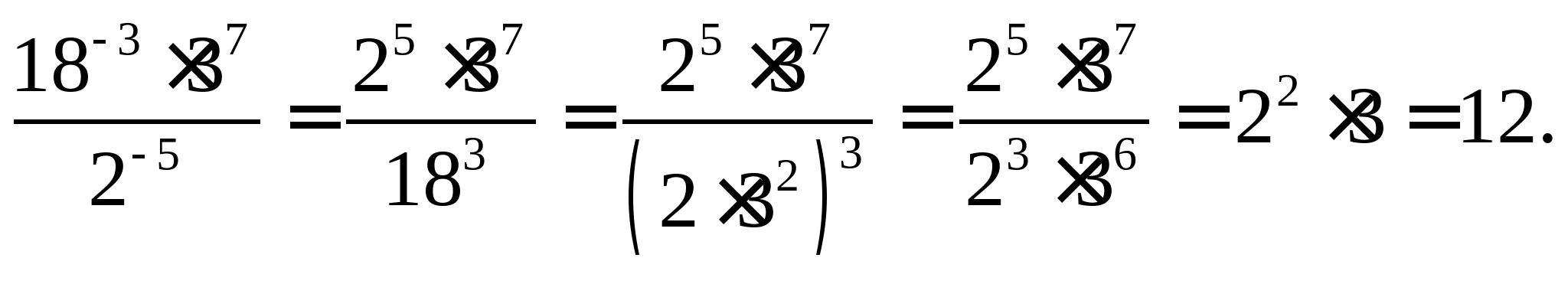
Приклад 2. Знайти значення виразу: 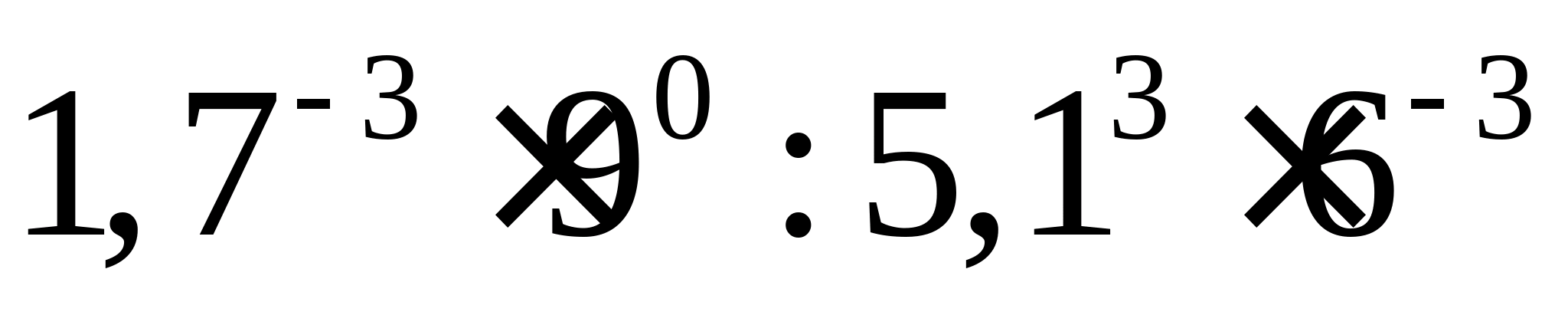 .
.
Приклад 3. Спростити: 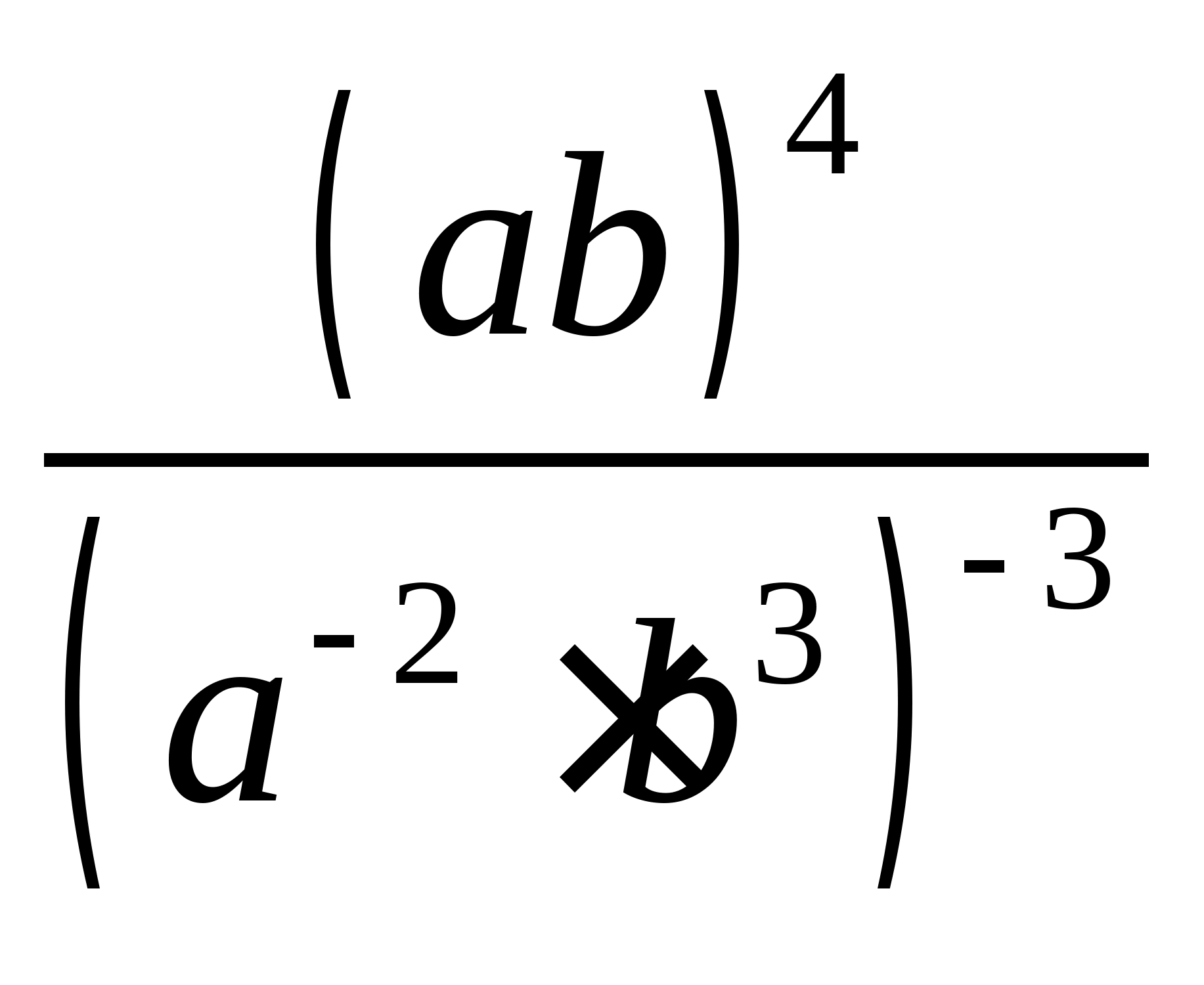 .
.
Рішення. 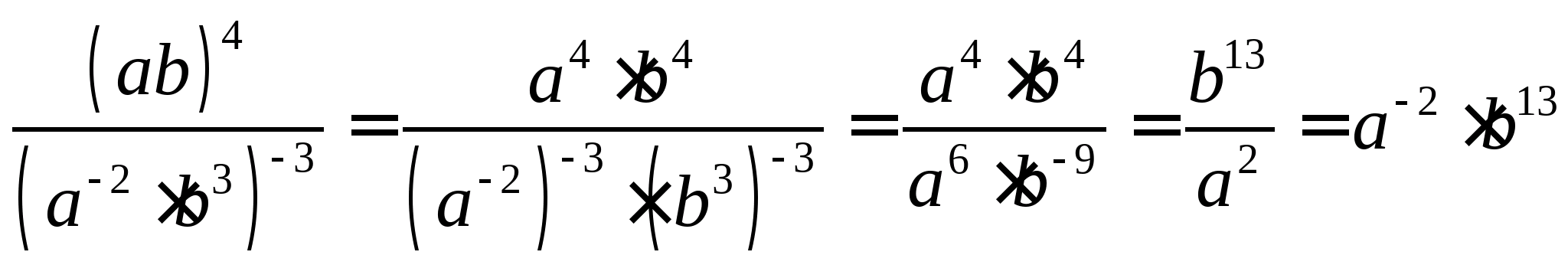 .
.
2.3. Арифметичний корінь n-й ступеня
Визначення: Коренем п-й ступеня з числа називається число, п-я ступінь якого дорівнює а.
Якщо n=2 , маємо квадратний корінь. Якщо n=3 , то корінь називається кубічним.
Якщо а>0і b-корінь парної n-й ступеня (n=2 k), то й (- b) також є коренем n- ступеня з числа а, т.к. (- b) n =(- b) 2 k =(b) 2 k =(b) n = a.
Дія знаходження кореня n-й ступеня з числа називається вилученням кореня n-й ступеня. Ця дія є зворотною до зведення в n-ю ступінь.
Якщо a<0 , то корінь парний n-й ступеня з числа ане існує (на безлічі дійсних чисел).
Визначення: Арифметичним коріннямn-й ступеня з неотрицательного числа називається неотрицательное числоb, n-Ступінь якого дорівнює а.
Наприклад, числа 3 і -3 є корінням четвертого ступеня з числа 81 . При цьому число 3 - арифметичний корінь четвертого ступеня з числа 81 , а число -3 не є арифметичним коренем.
Арифметичний корінь n-й ступеня з числа  позначається так:
позначається так: 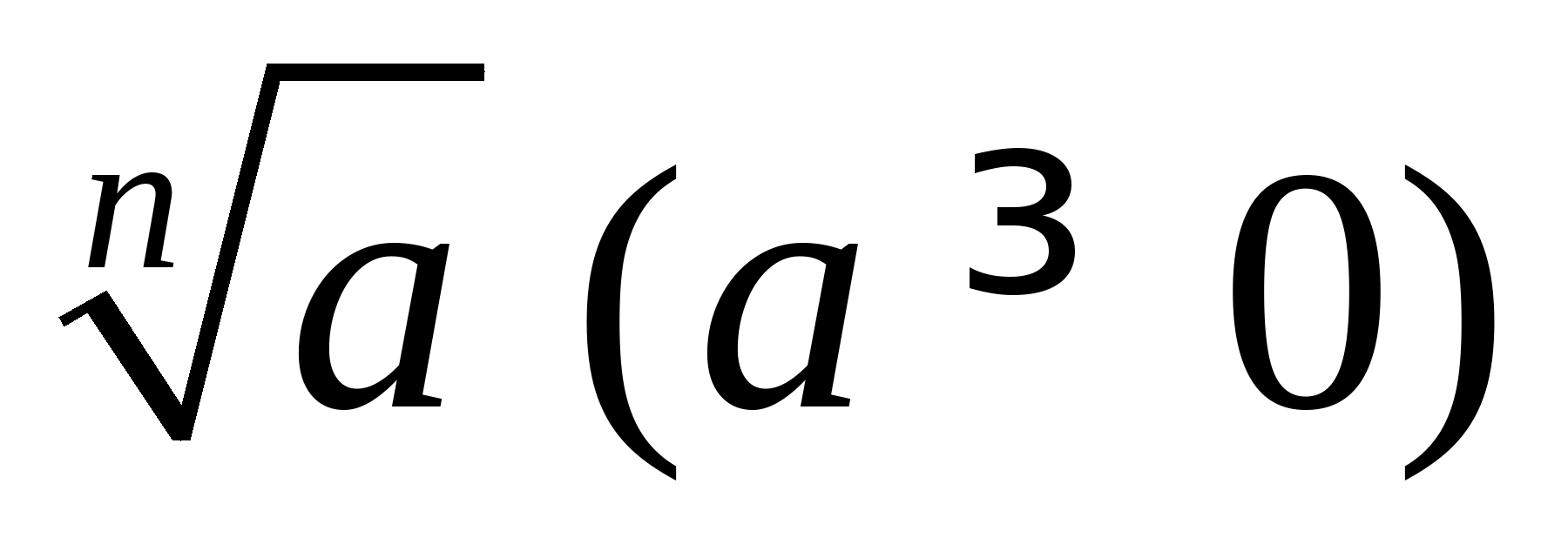 ; аназивається підкореним числом, а натуральне число n (n≥2)
- Показником кореня.
; аназивається підкореним числом, а натуральне число n (n≥2)
- Показником кореня.
Якщо n=2
показник кореня не пишеться. Наприклад, замість 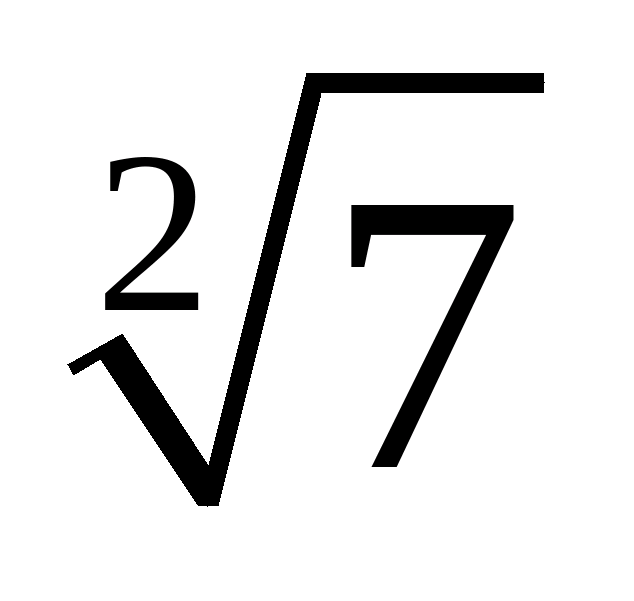 , пишуть
, пишуть 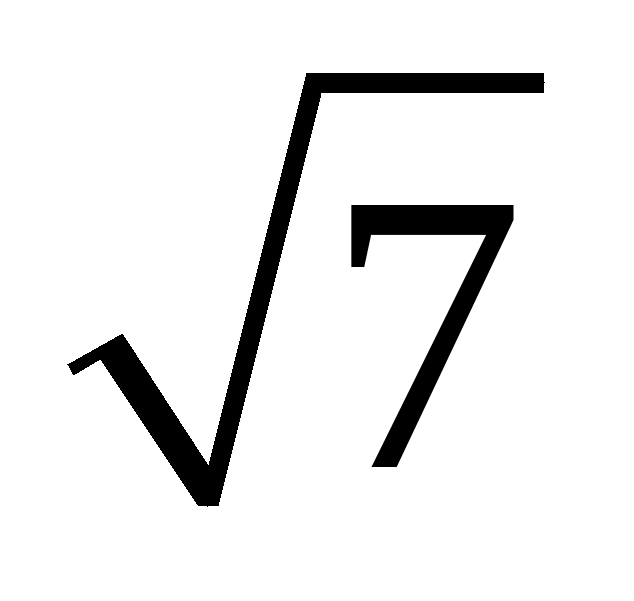 .
.
Теорема. З будь-якого дійсного числа а≥0можна отримати арифметичний корінь n- й ступеня і до того ж тільки один.
Корінь парного ступеня із негативного числа не існує.
Корінь непарного ступеня з негативного числа – число негативне..
Цей корінь єдиний і позначається як і, як і арифметичний.
Корінь непарний n-й ступеня з негативного числа апов'язаний з арифметичним коренем з числа -а = | а |наступною рівністю:
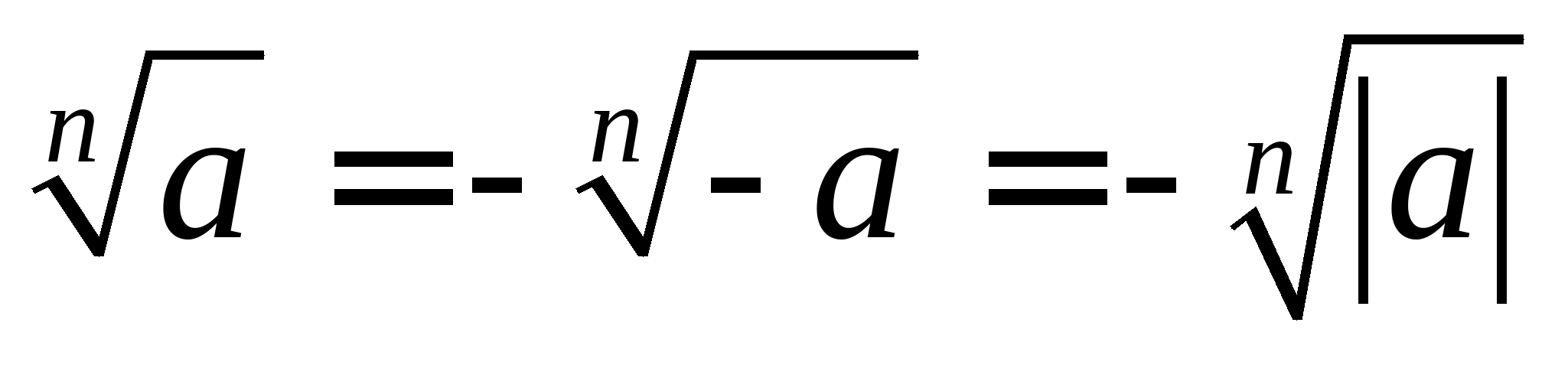 , де a<0
, n-непарне натуральне число (N≥3).
, де a<0
, n-непарне натуральне число (N≥3).
Надалі запис виду 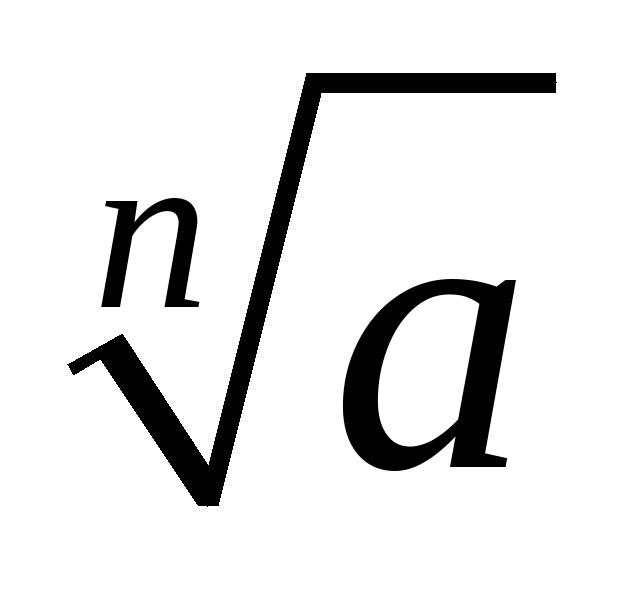 буде означати арифметичний корінь, коли а≥0, або корінь непарного ступеня з негативного числа, коли а<0
.
буде означати арифметичний корінь, коли а≥0, або корінь непарного ступеня з негативного числа, коли а<0
.
Властивості арифметичного кореня:
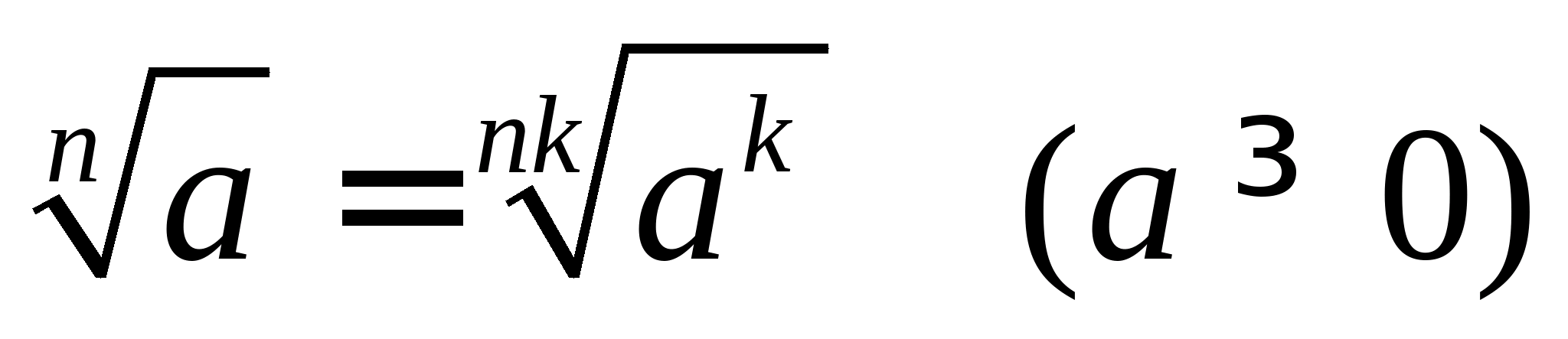
якщоa>
b>0, то 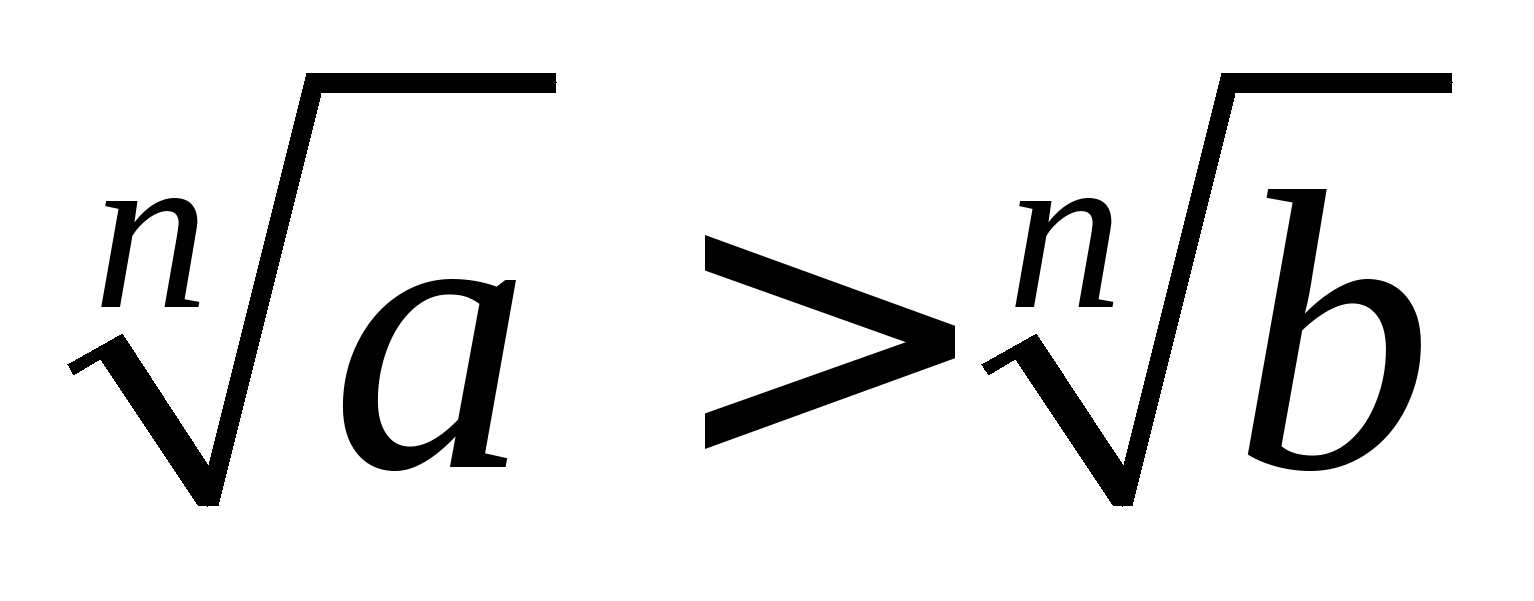 , і назад: якщо (a>0,
b>0), тоa>
b.
, і назад: якщо (a>0,
b>0), тоa>
b.
Довести: 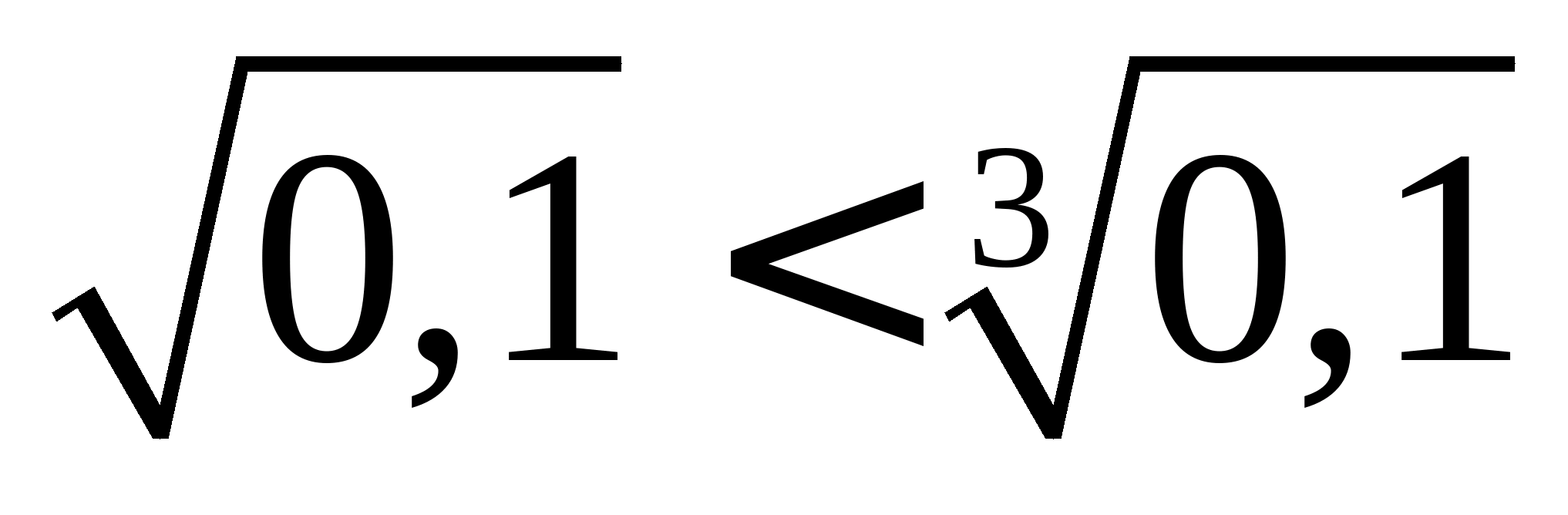 . Для доказу застосуємо основну властивість арифметичного кореня і наведемо коріння до загального показника 6 (найменшого загального кратного показника цих коренів): Оскільки
. Для доказу застосуємо основну властивість арифметичного кореня і наведемо коріння до загального показника 6 (найменшого загального кратного показника цих коренів): Оскільки 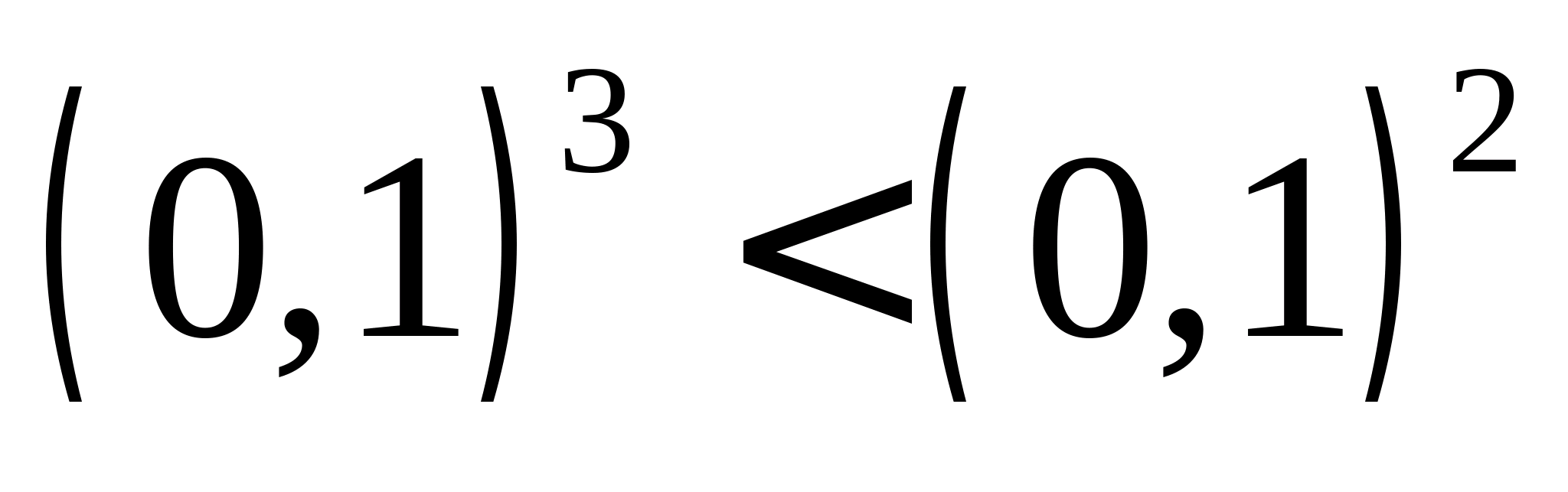 , то за якістю порівняння арифметичних коренівотримаємо: .
, то за якістю порівняння арифметичних коренівотримаємо: .
Зауваження: Для кореня непарного ступеня із негативного числа справедлива формула: .
За допомогою цієї формули можна показати, що властивості 2÷5 арифметичних коренів справедливі також і для коріння непарного ступеня негативного числа.
У випадку, як у перетвореннях беруть участь як арифметичні, і коріння непарної ступеня з негативного числа, ці властивості неправильні.
Наприклад, для твору 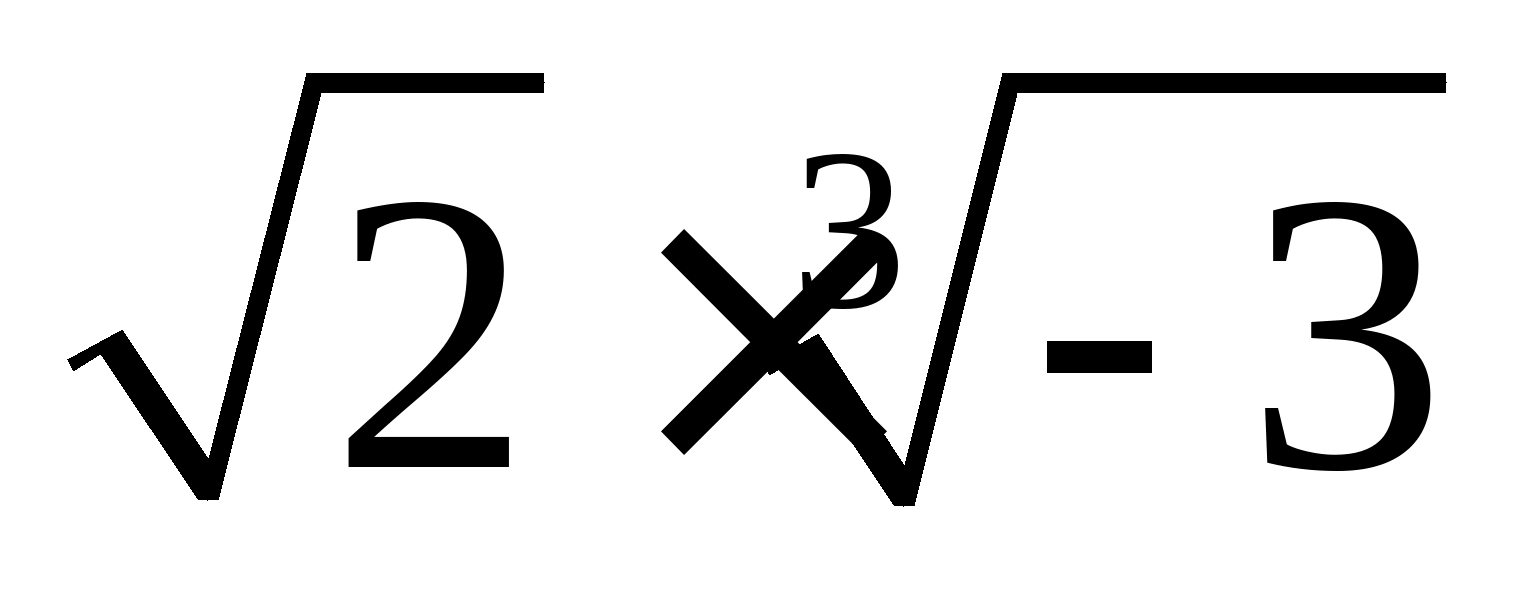 застосування властивостей 1. та 2. призведе до невірного результату:
застосування властивостей 1. та 2. призведе до невірного результату: 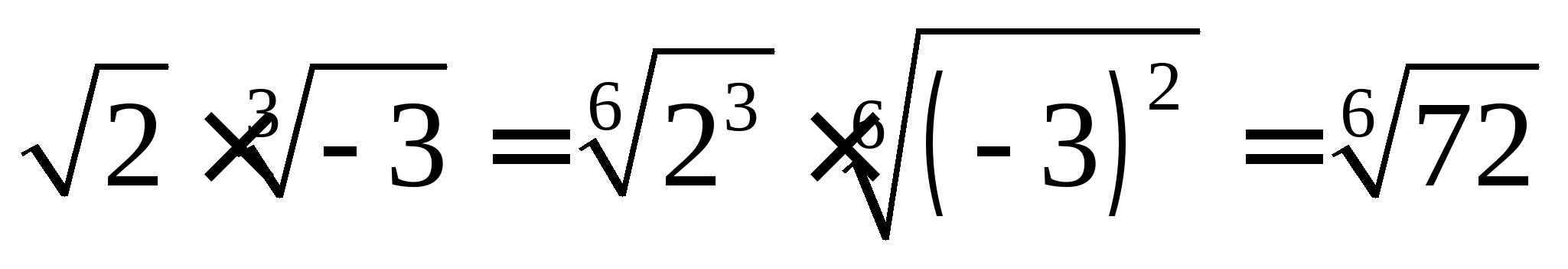 .
.
Правильне рішення: .
У разі арифметичного квадратного коренябуло доведено, що 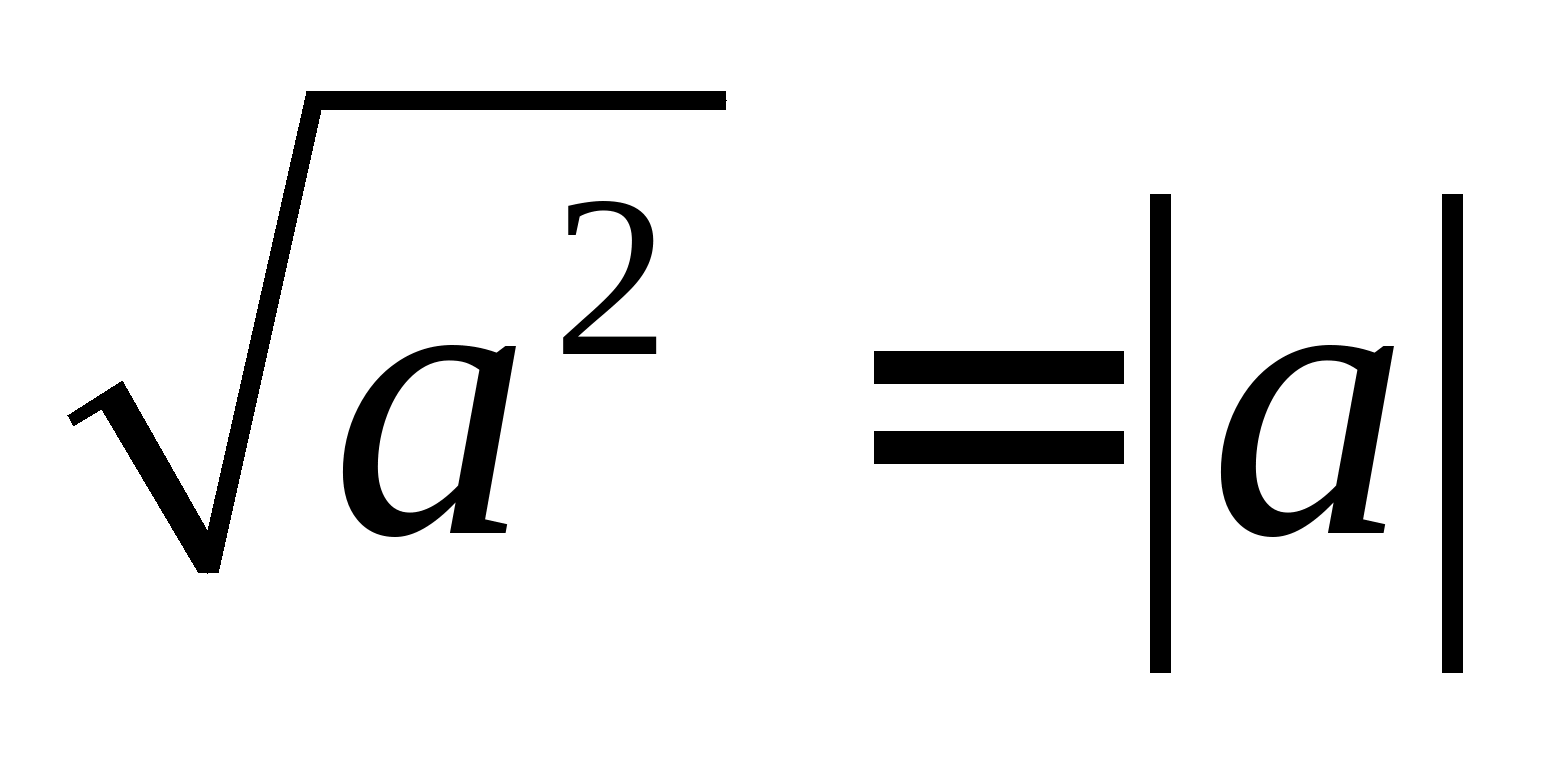 для будь-якої дійсної кількості а. Аналогічно:
для будь-якої дійсної кількості а. Аналогічно:
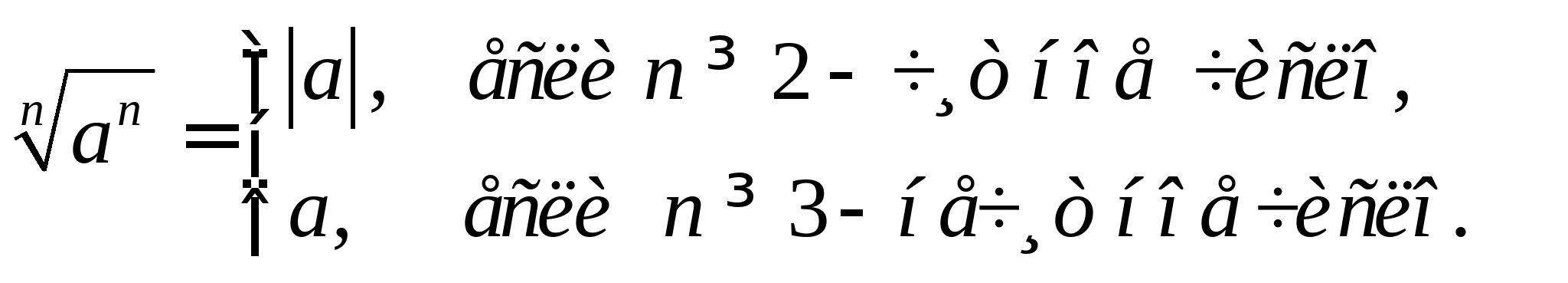
Наприклад, у перетвореннях:
Приклад 1. Внести множник під знак кореня у виразі: 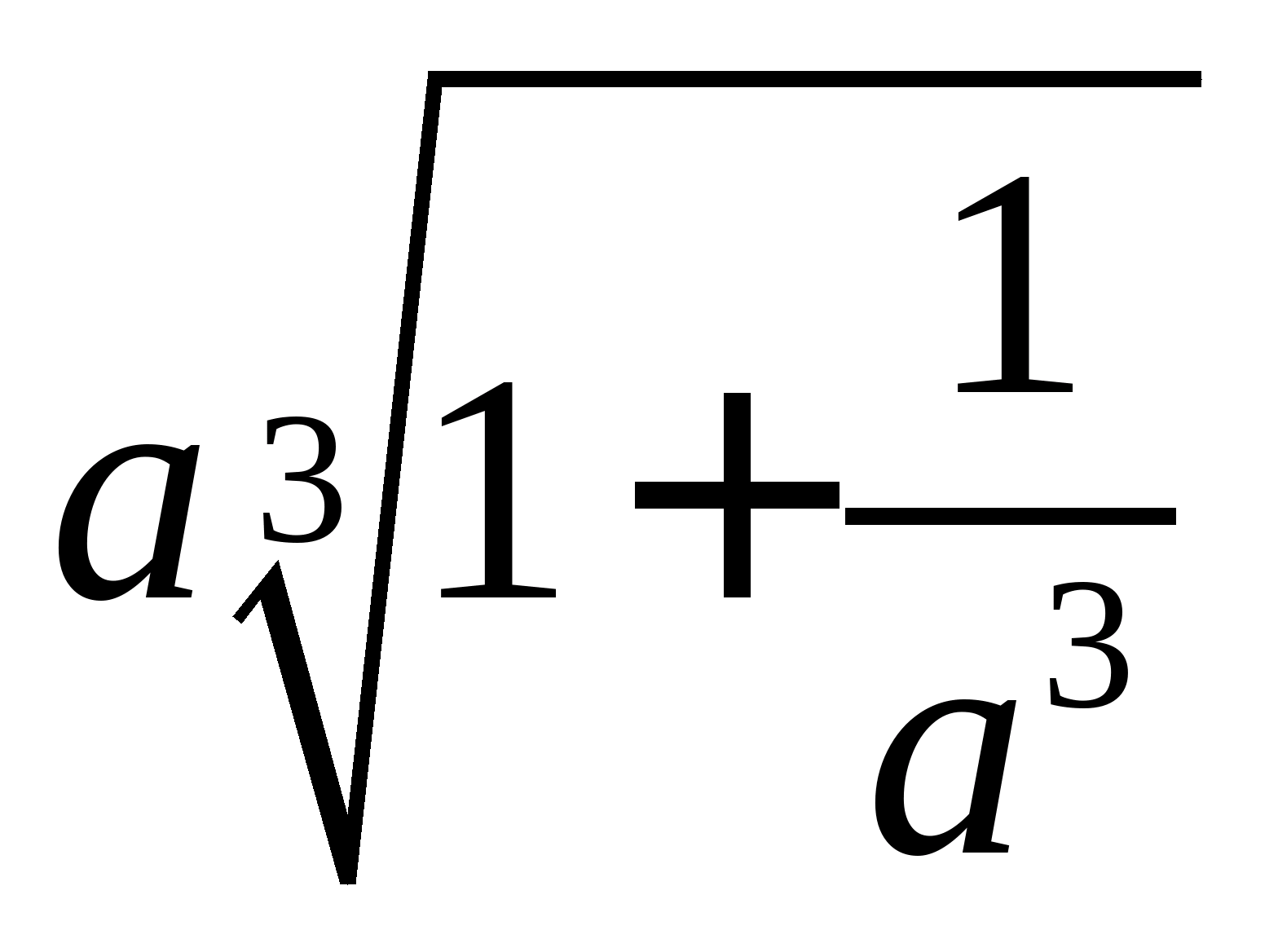 .
.
Рішення. Так як 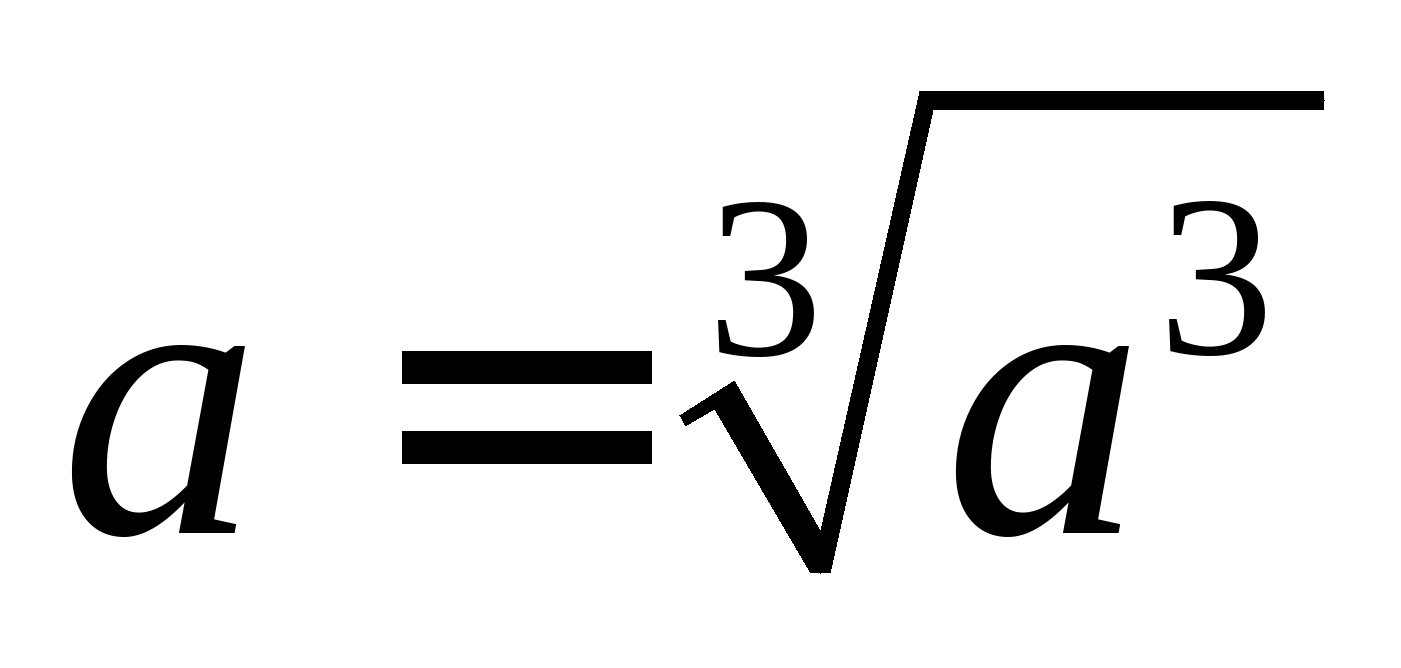 , то
, то
Приклад 2. Винести множник з-під знаку кореня у виразі: 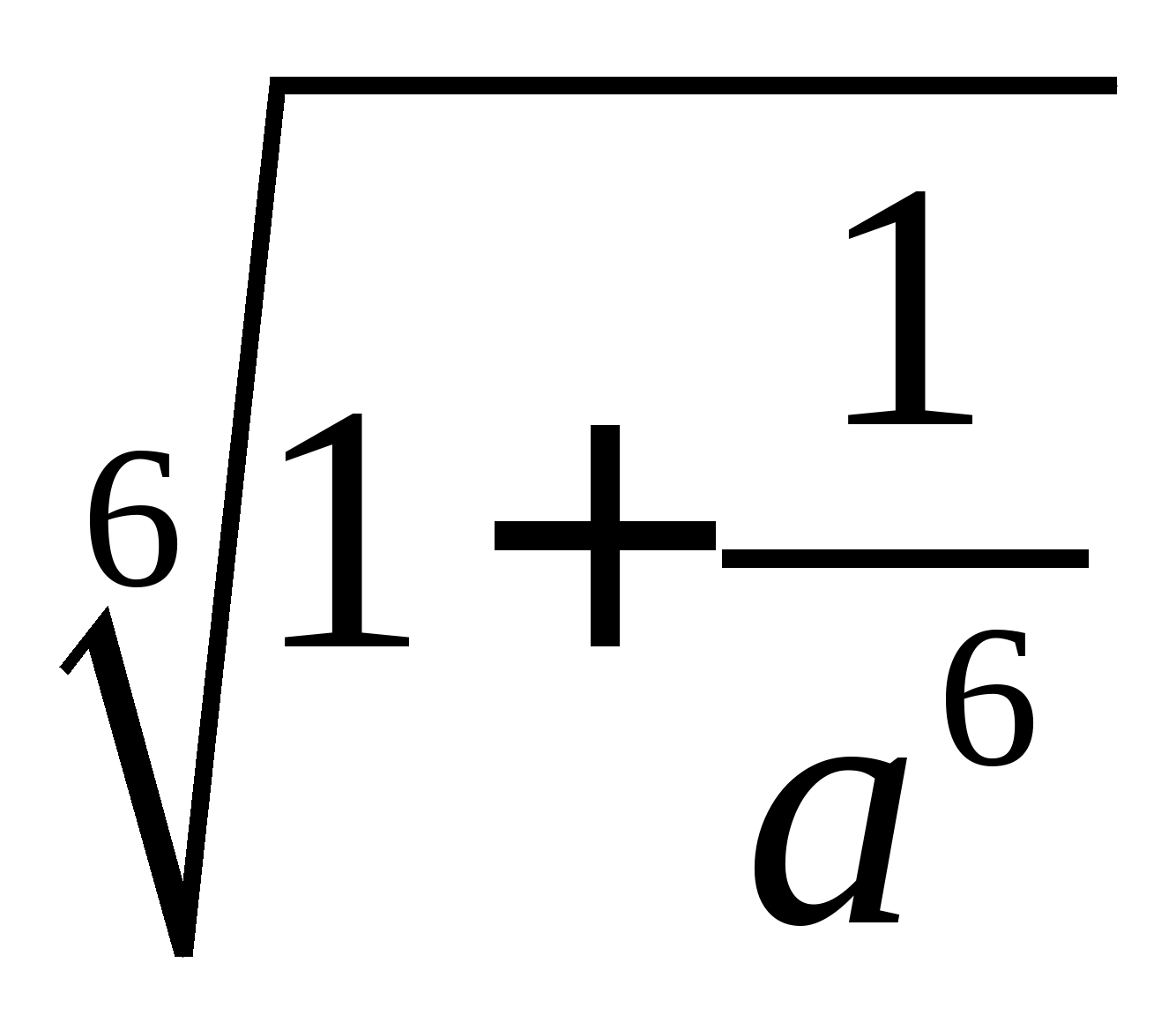 , де а<0.
, де а<0.
Рішення. 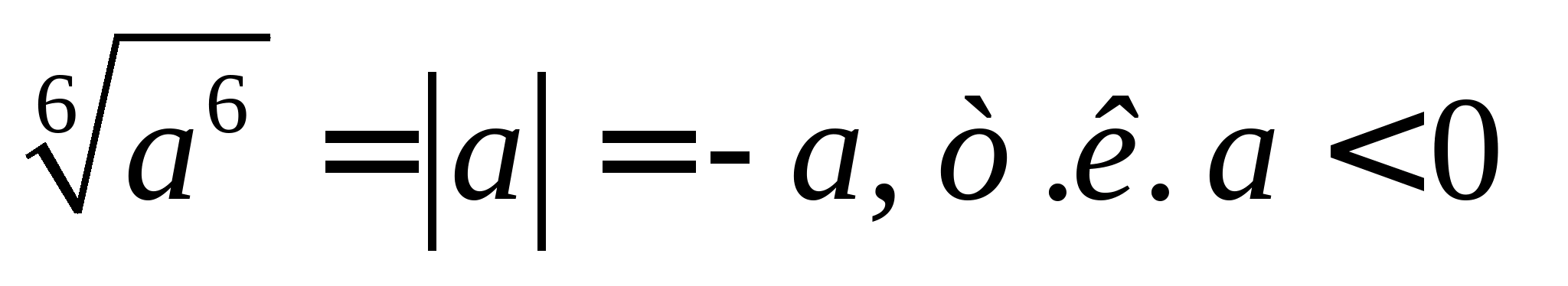 , то
, то 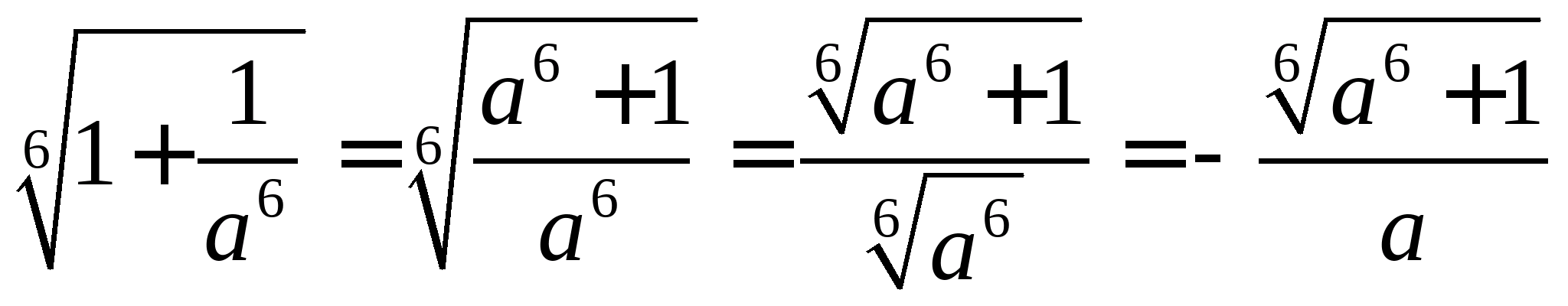 .
.
Приклад 3. Виконати дії: 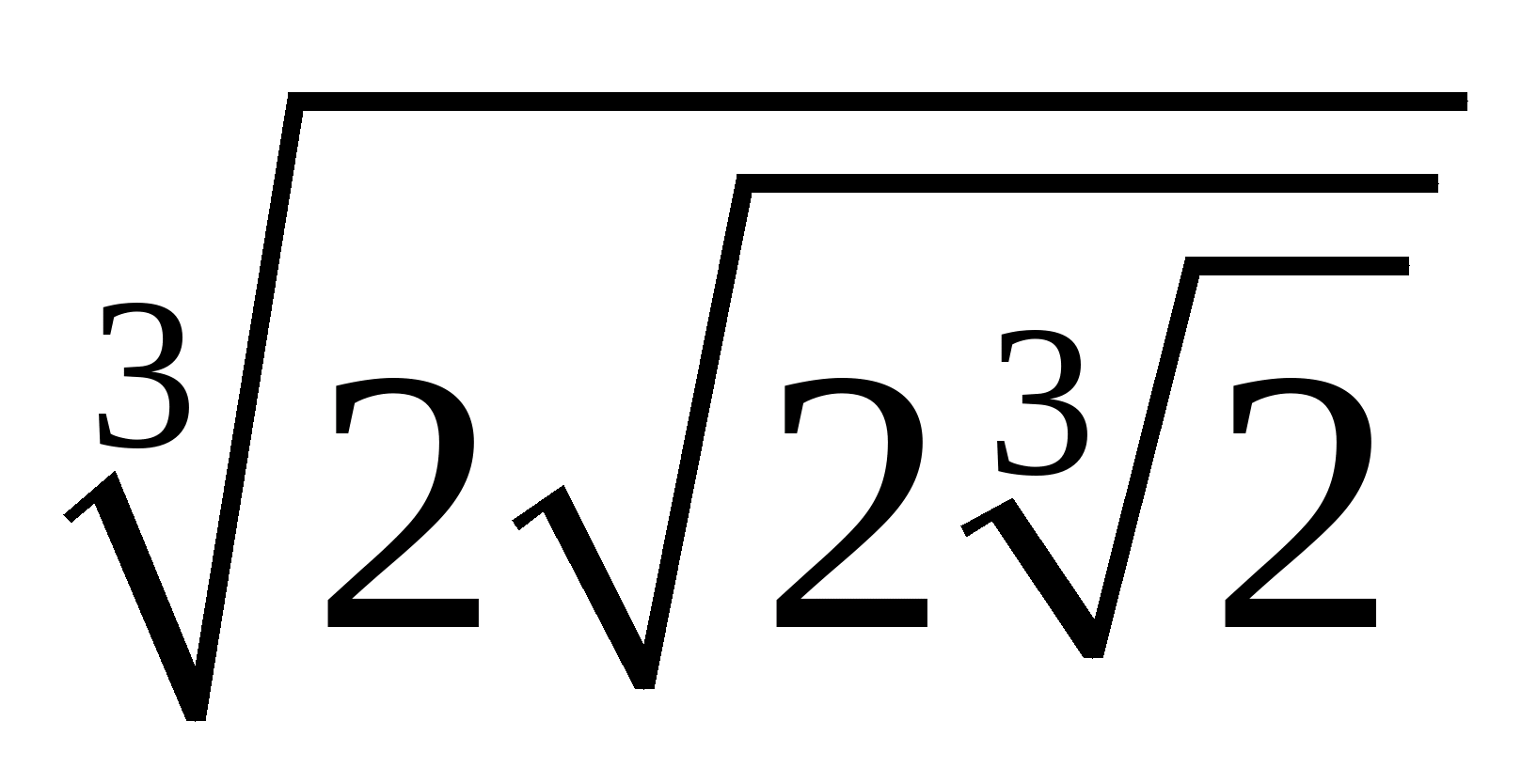 .
.
Рішення. 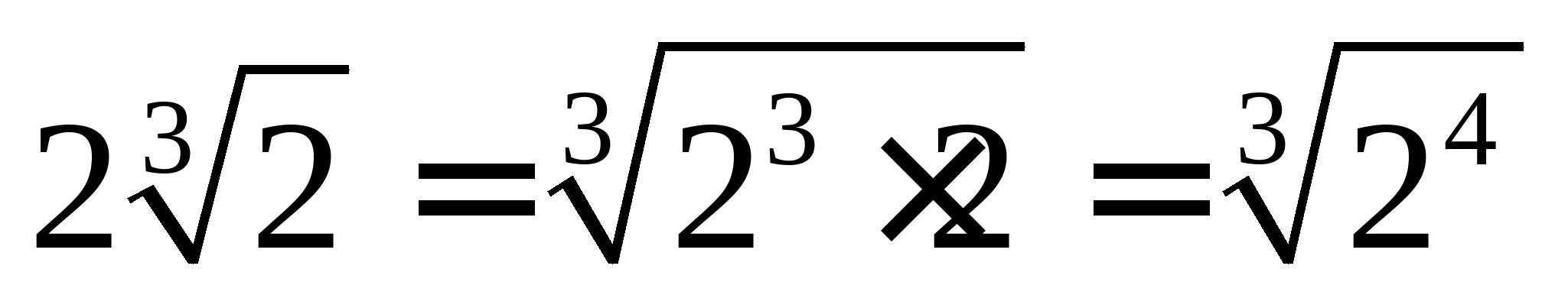 ; .
; .
2.4. Ступінь з раціональним показником
Поняття та властивості ступеня з будь-яким цілим показником були розглянуті вище.
Введемо тепер на розгляд ступінь із дробовим показником.
Визначення. Якщоa>0 таx– раціональне число, подане дробом 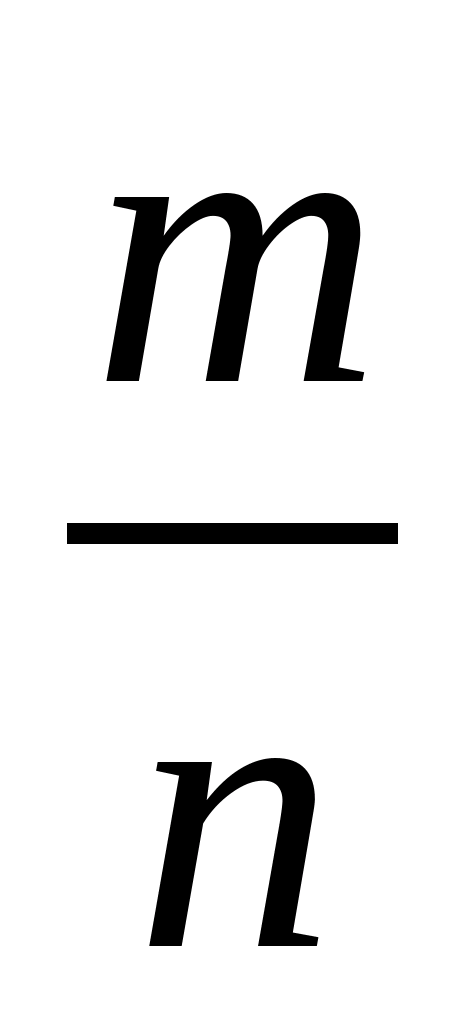 , деm- ціле, іn≥2 – натуральне число, то:
, деm- ціле, іn≥2 – натуральне число, то: 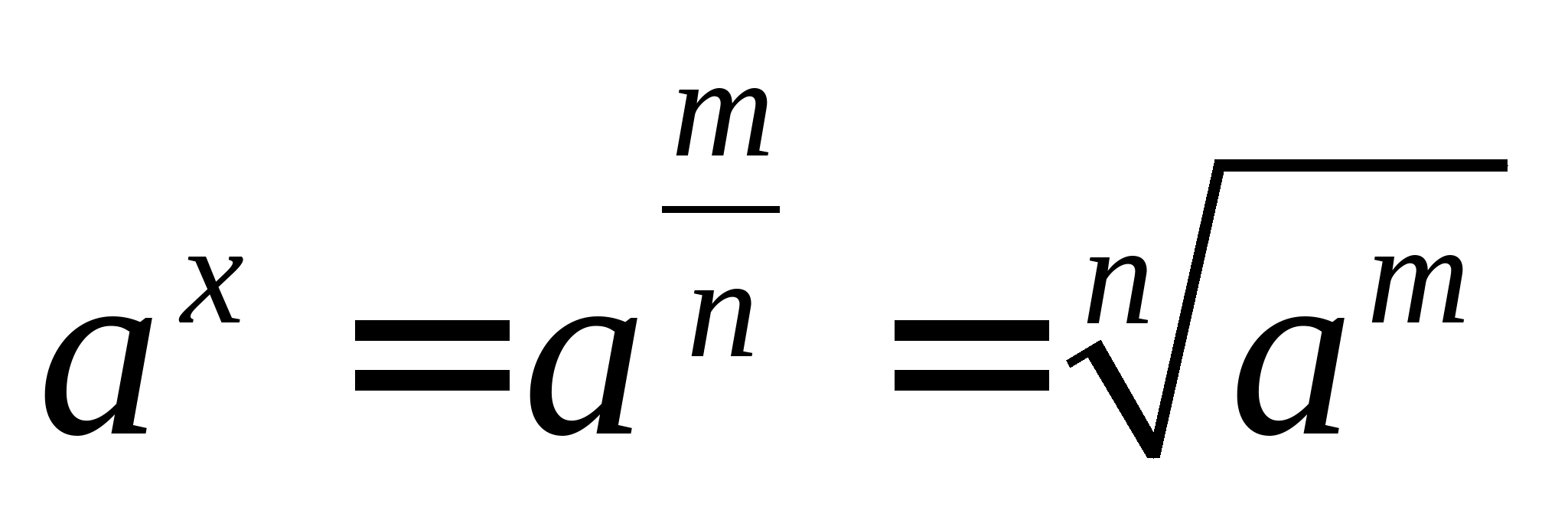 ; якщо а
; якщо а 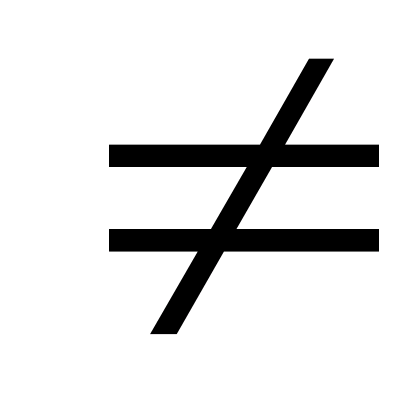 0 таx>0, тоa x
0.
0 таx>0, тоa x
0.
Наприклад, 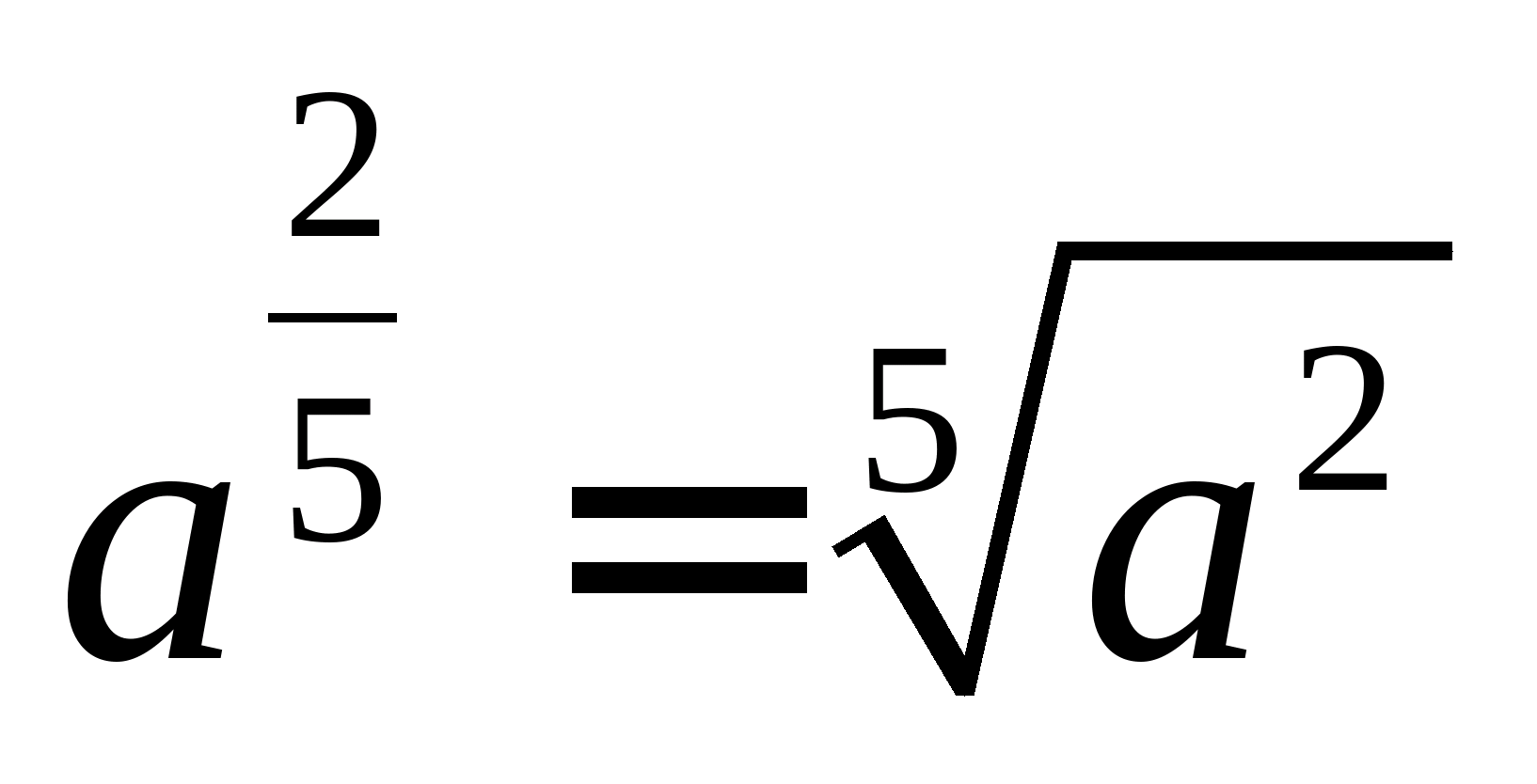 при а≥0;
при а≥0; 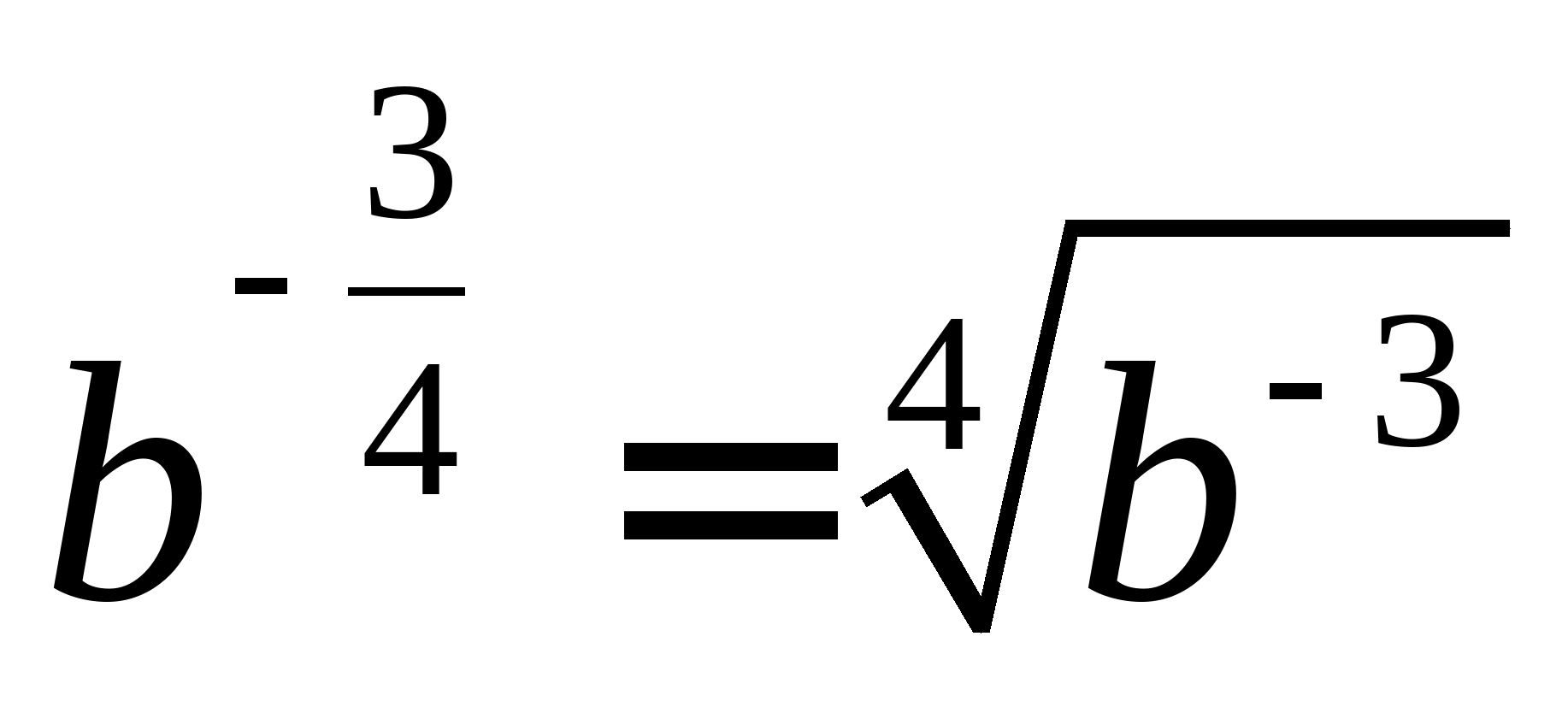 або
або 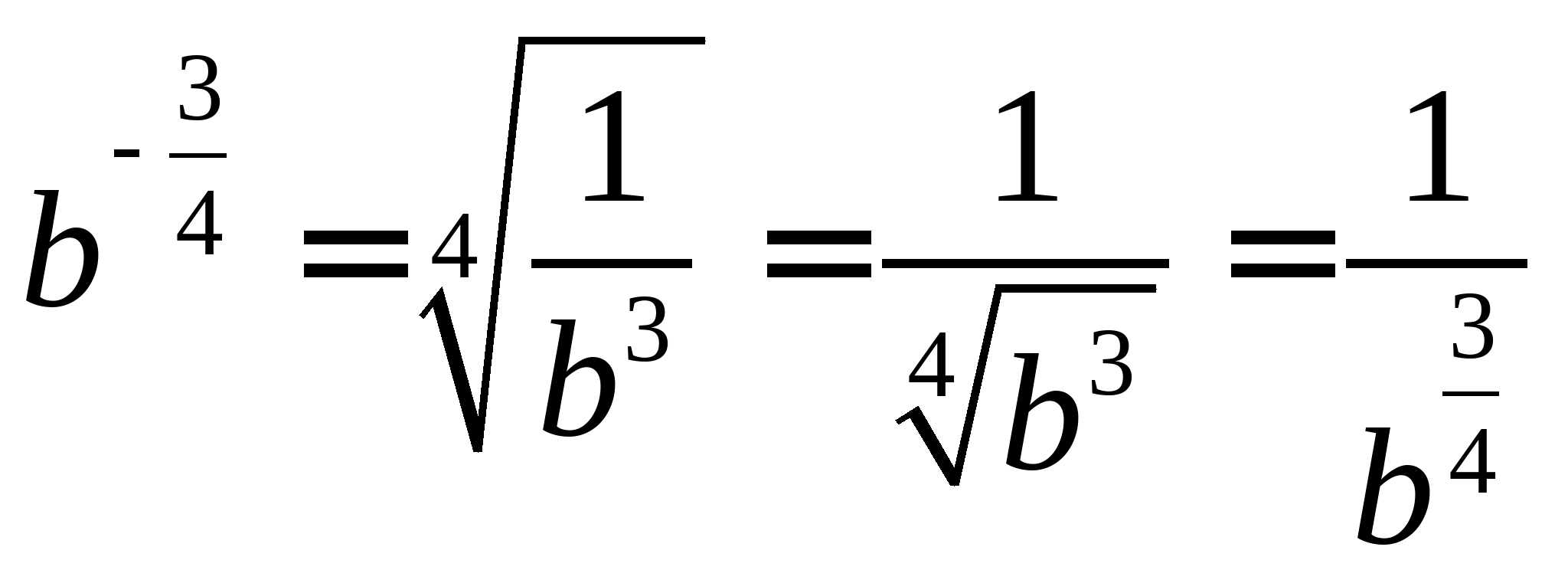 при b>0
.
при b>0
.
Раціональне число представляється як дробу неоднозначно, оскільки 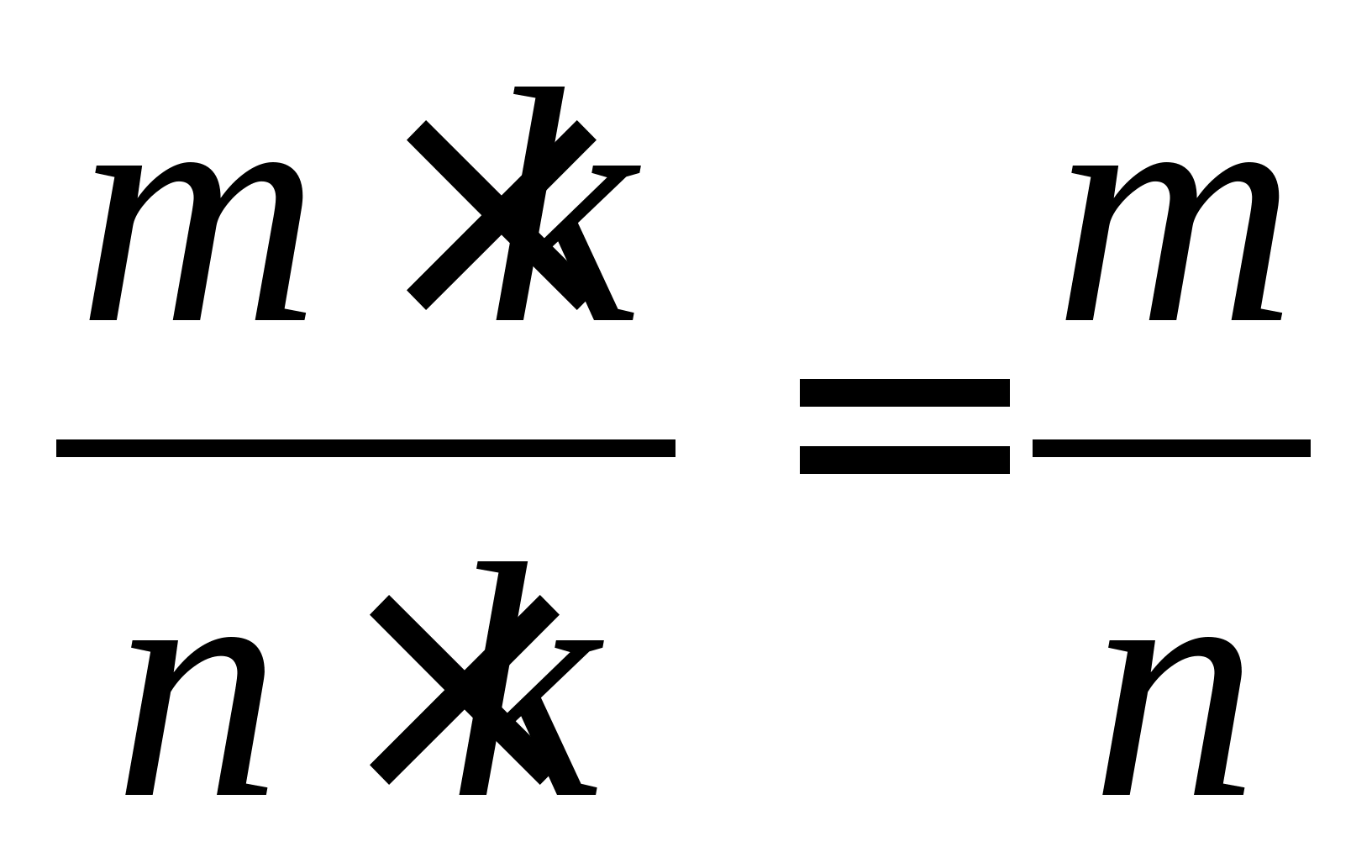 при будь-якому натуральному k.
при будь-якому натуральному k.
Покажемо, що: 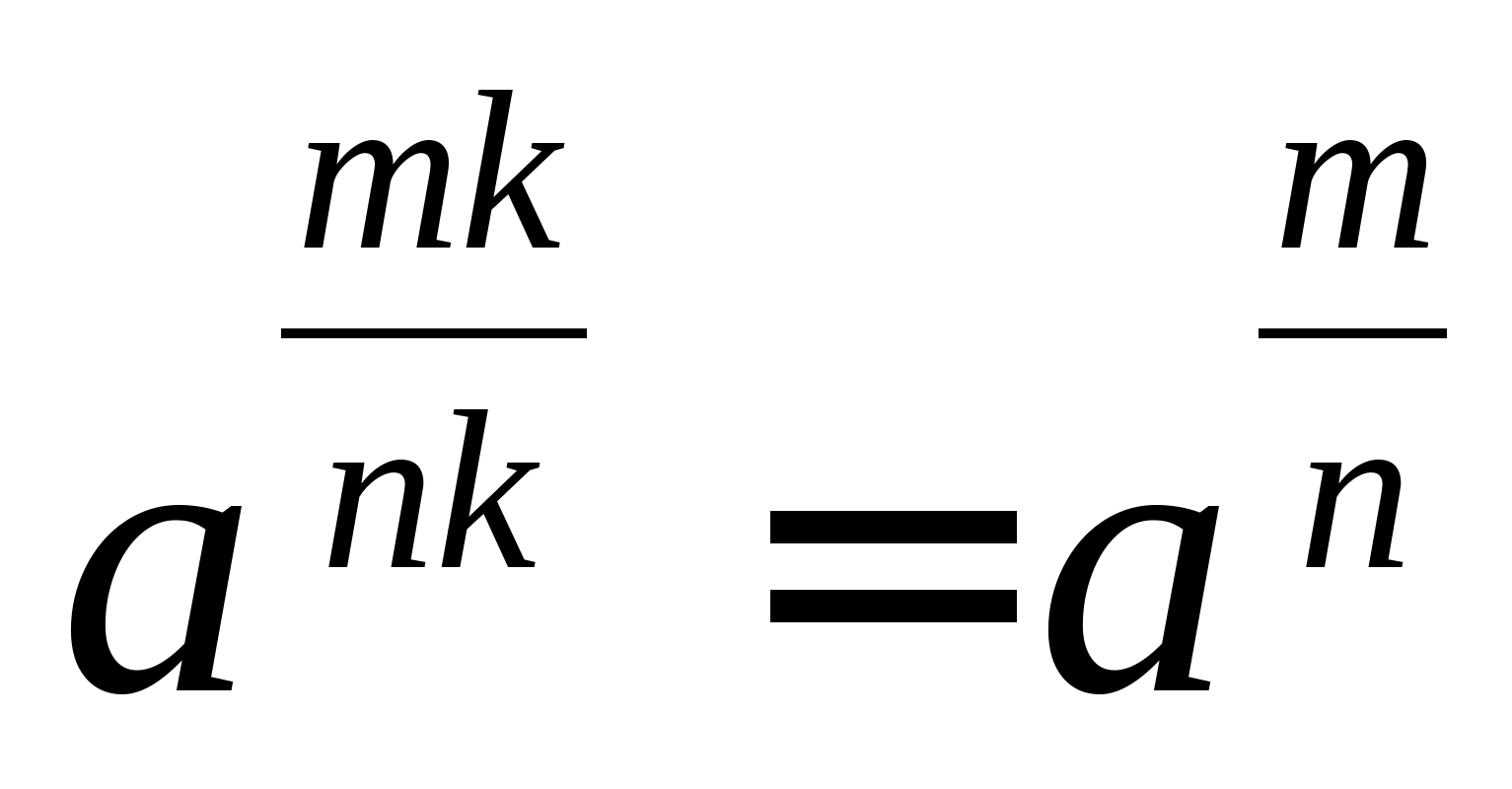 . Справді:
. Справді: 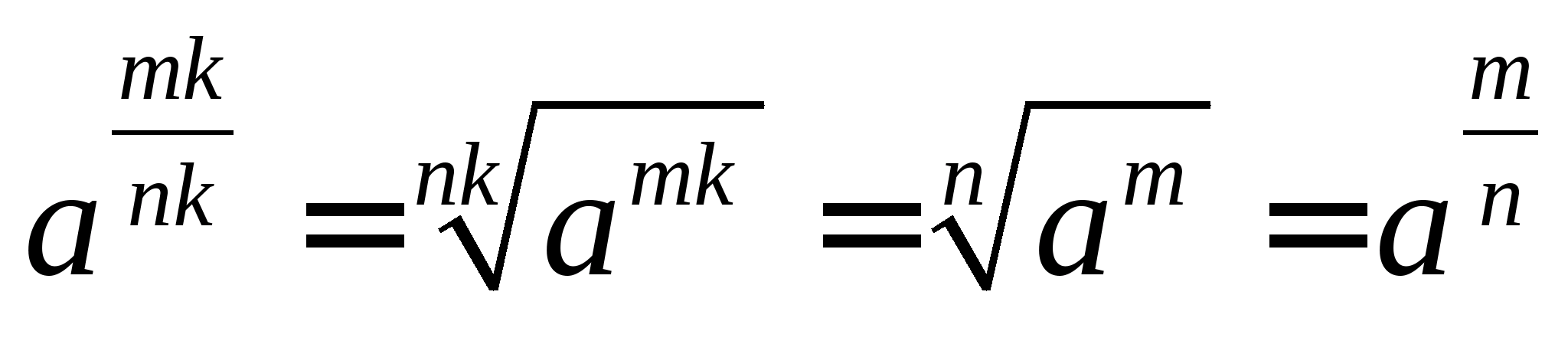 (Використана основна властивість арифметичного кореня).
(Використана основна властивість арифметичного кореня).
Властивості функції з цілим показником поширюються на ступінь з будь-яким раціональним показником та позитивною основою, наприклад: a p ∙ a q = a p + q (a>0).
2.5. Приклади обчислення арифметичних виразів зі ступенями
Приклад 1. Обчислити: 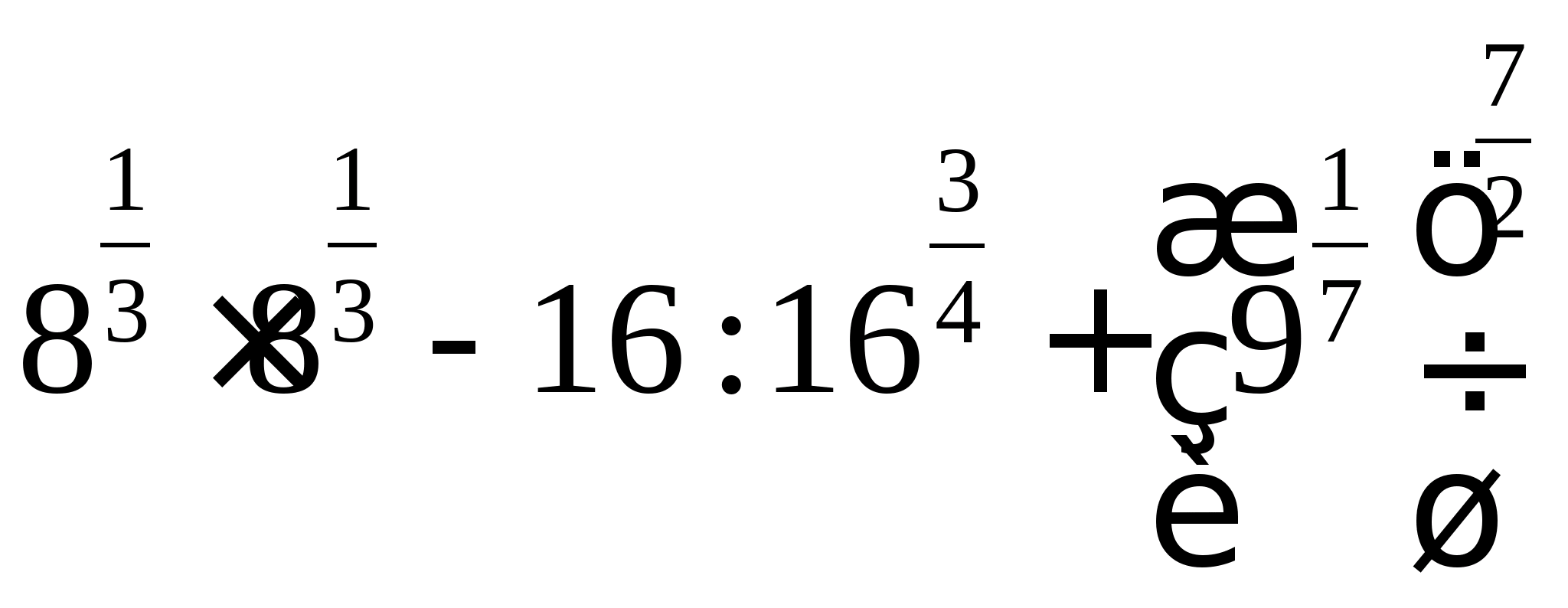 .
.
Рішення. ; 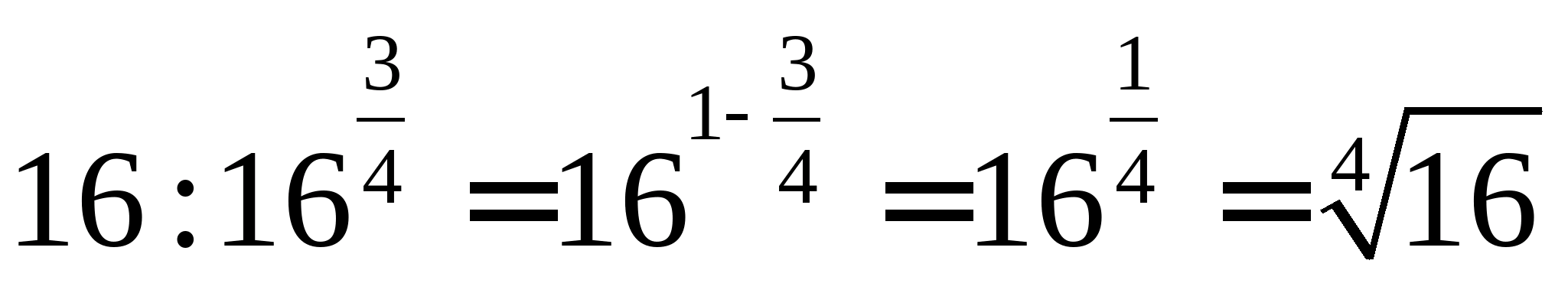 ;
;
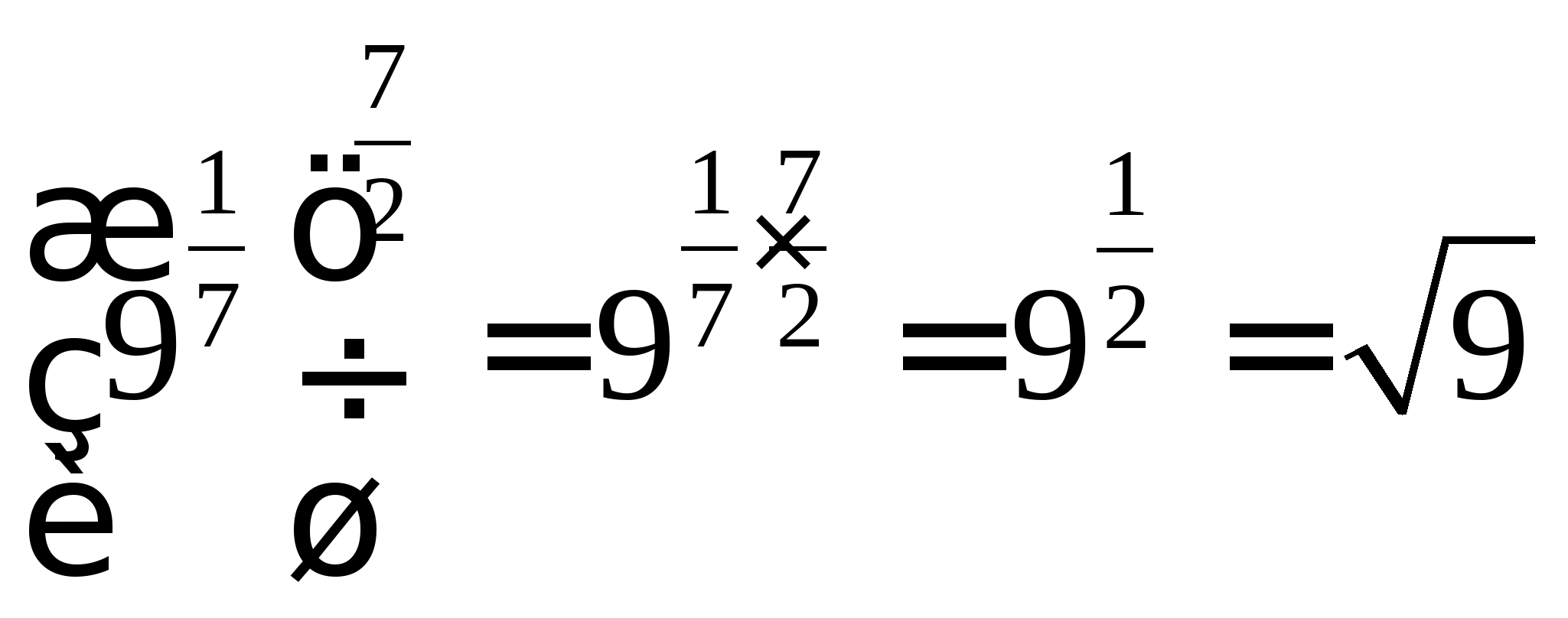 . Звідси: .
. Звідси: .
Приклад 2. Виконати дії: 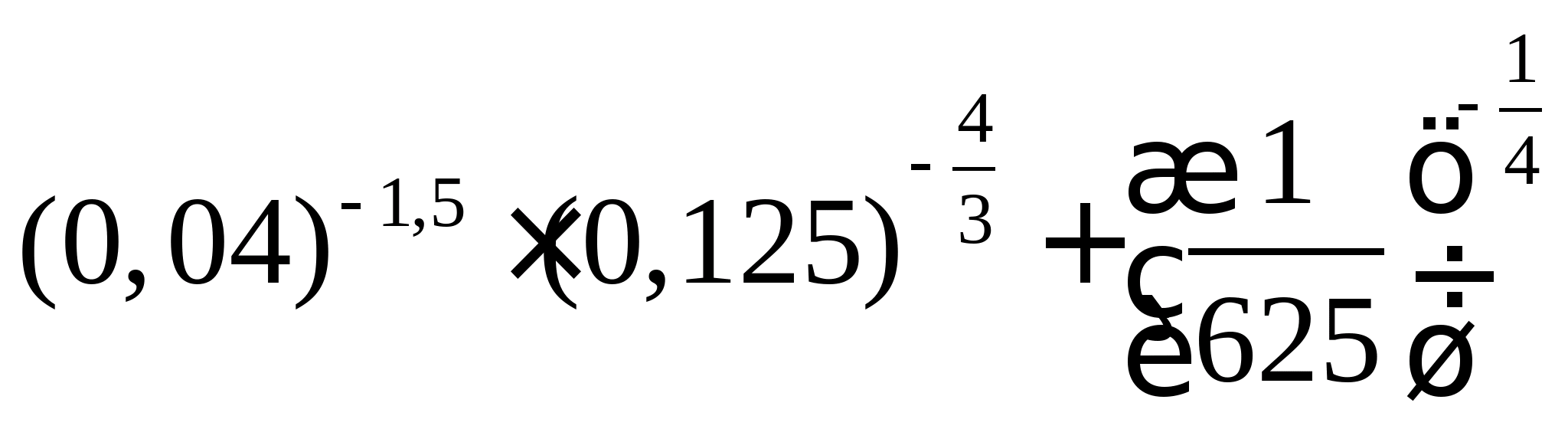 .
.
Рішення. 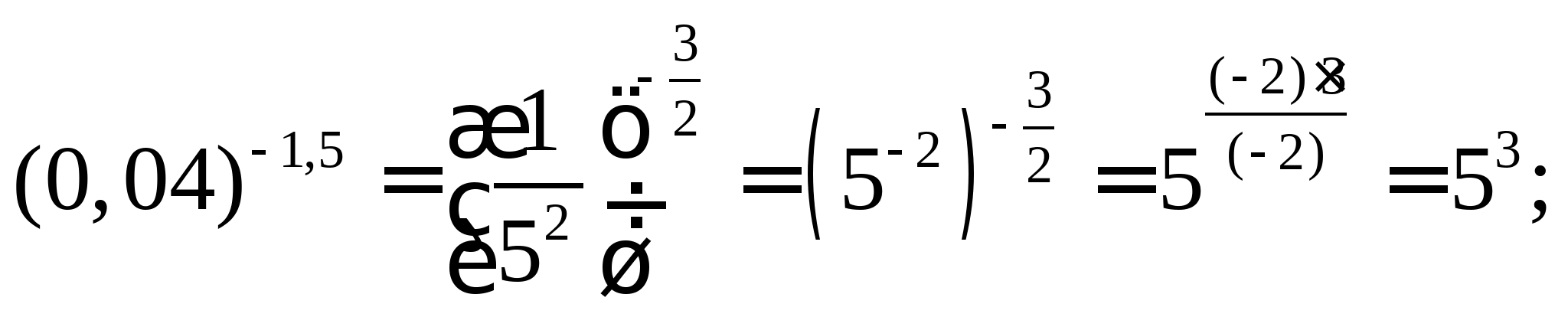
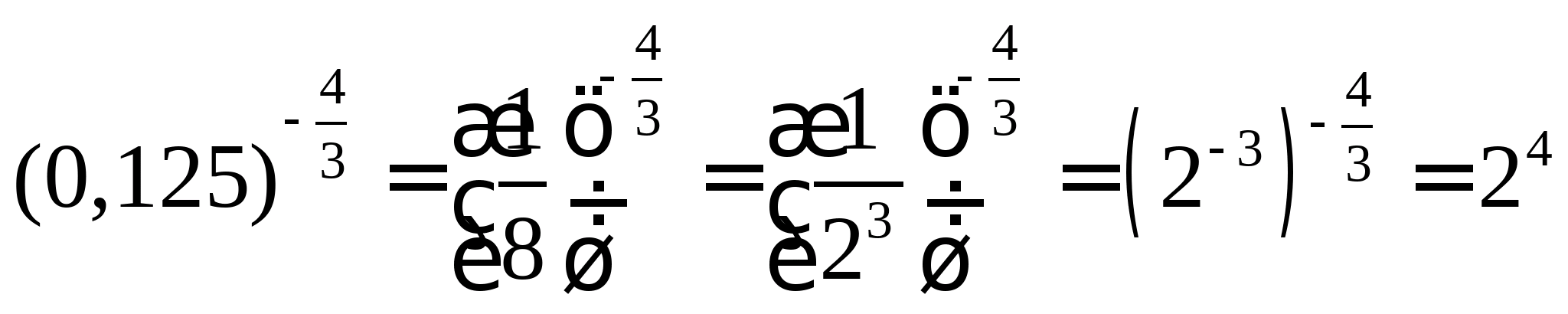 ;
; 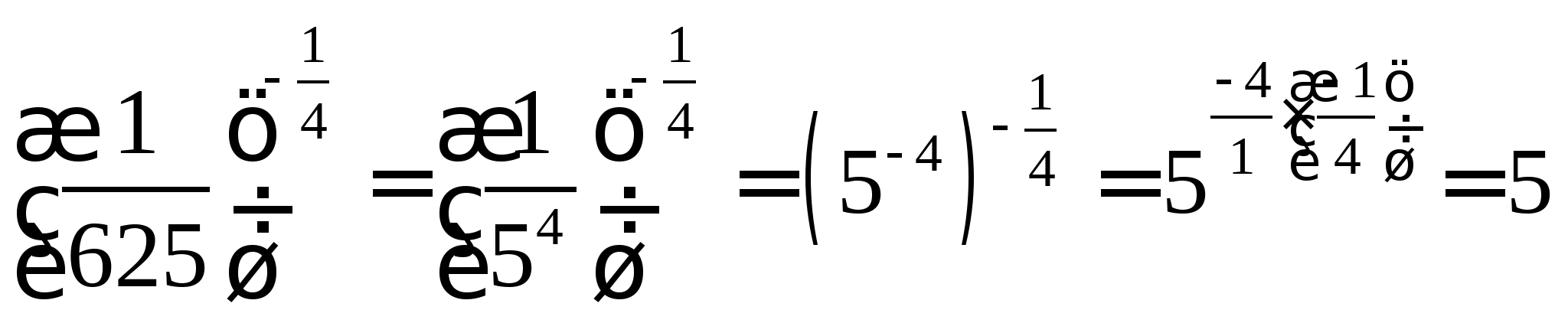 .
.
Звідси: 5 3 ∙2 4 +5=(5∙2) 3 ∙2+5=2000+5=2005 .

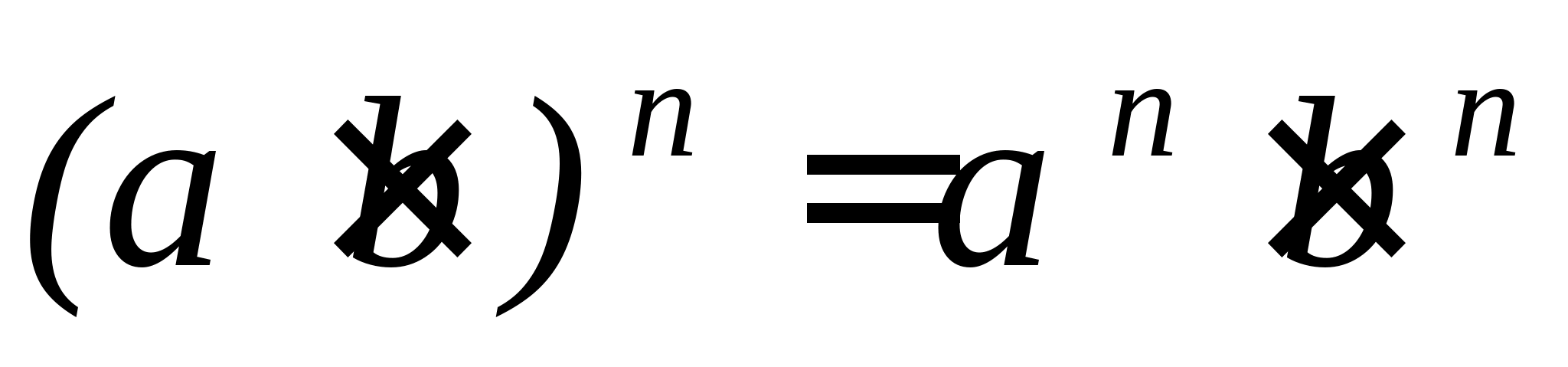
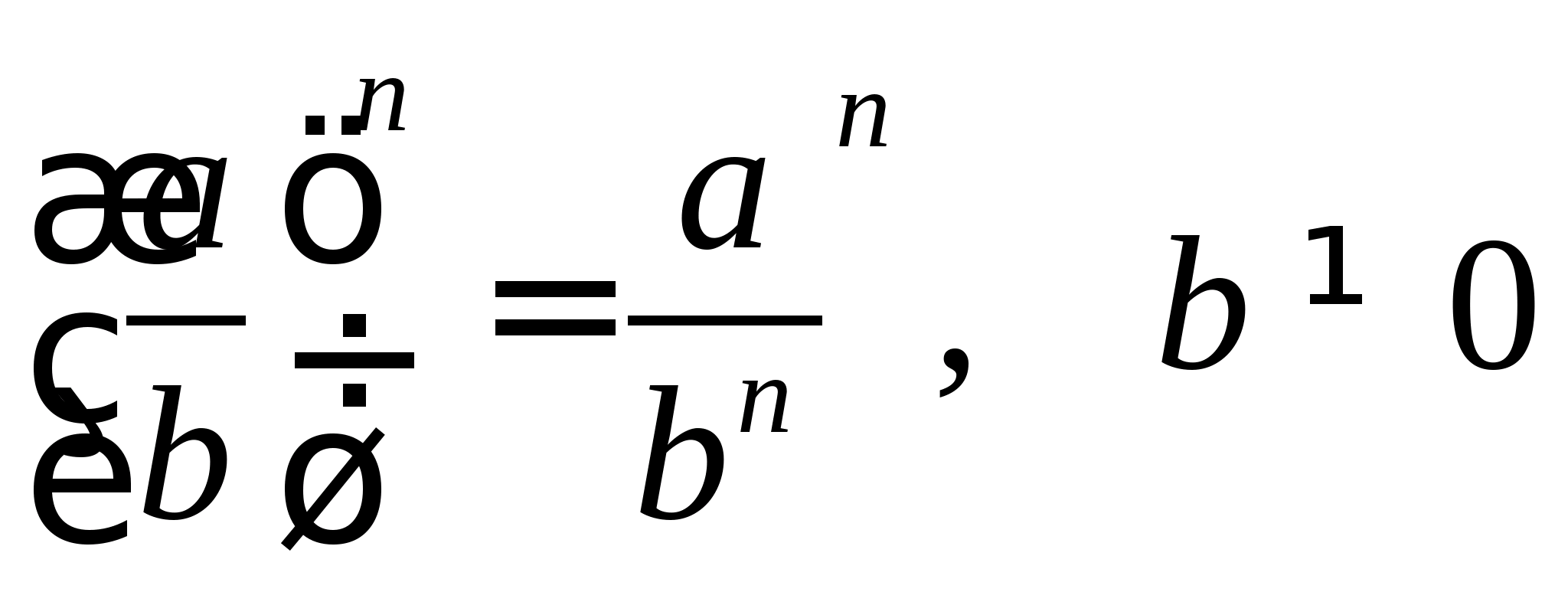 ;
;