Як застосовують прийом порівняння із проміжним числом. Порівняння чисел. Середній рівень
Муніципальне бюджетне загальноосвітнє «Ліцей №4» м.о.Коломна
Конспект майстер-класу
тема
«ХИТРІ» СПОСОБИ ПОРІВНЯННЯ ЗВИЧАЙНИХ ДРОБІВ
Заступник директора з УВР, учитель математики І категорії
Ташпулатова Ноїла Разимівна
2016
Цілі: 1. Формувати здібності до побудови та використання
алгоритму порівняння звичайних дробів: а) способом
доповнення до 1; б) способом порівняння з проміжним
числом.
Повторити та закріпити: приведення дробів до найменшого загального чисельника, знаменника, порівняння дробів з однаковими чисельниками та знаменниками, алгоритм порівняння правильних та неправильних дробівскорочення дробів.
Тип уроку: "Відкриття" нового знання.
Епіграф: «Єдиний шлях, що веде до
знання – це діяльність ».
Б. Шоу
Хід уроку: 1.Організаційний момент.
Здрастуйте, шановні колеги! Я рада бачити Вас на своєму майстер -
класі і сподіваюся на взаємну співпрацю, яку вірю, доставить
задоволення, як мені, і Вам.
2. Актуалізація знань.
Відкрили зошити, записали число, класну роботу.
Виконання завдань:
Скоротіть дроби
Запишіть їх у порядку зростання 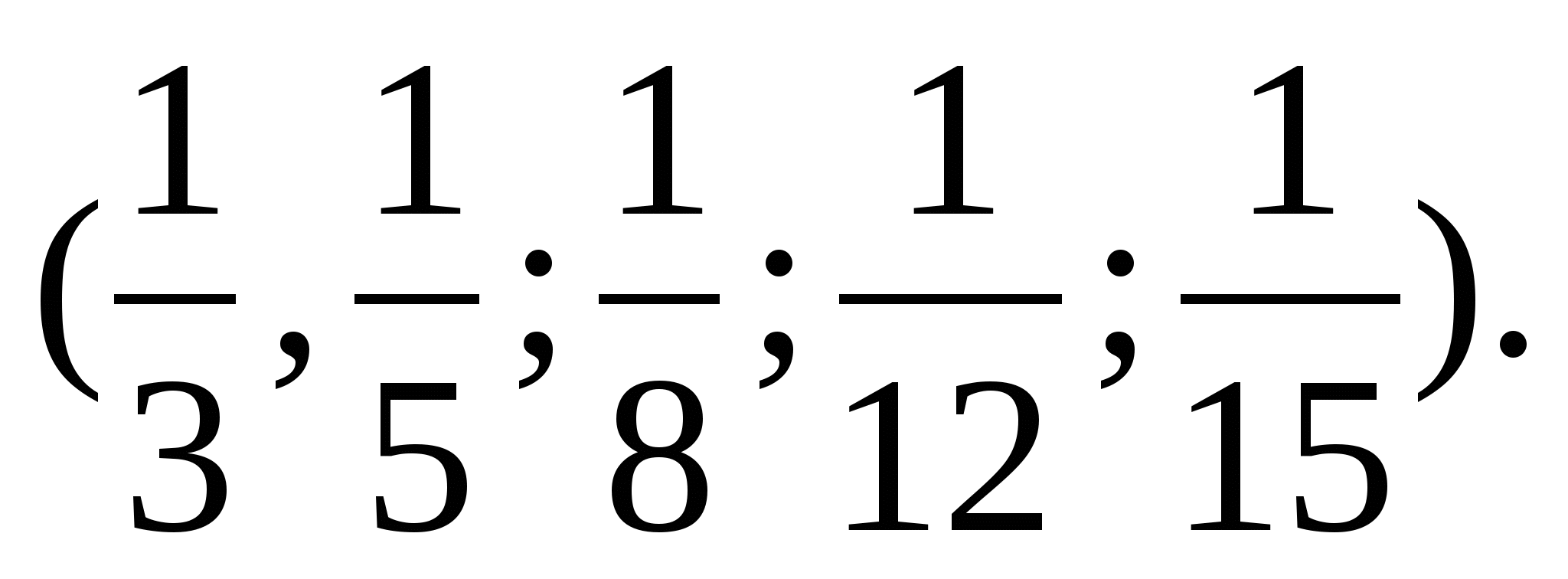
Яким способом порівняння Ви скористалися?
Які дроби треба додати до кожного з цих дробів, щоб у сумі
вийшла одиниця? 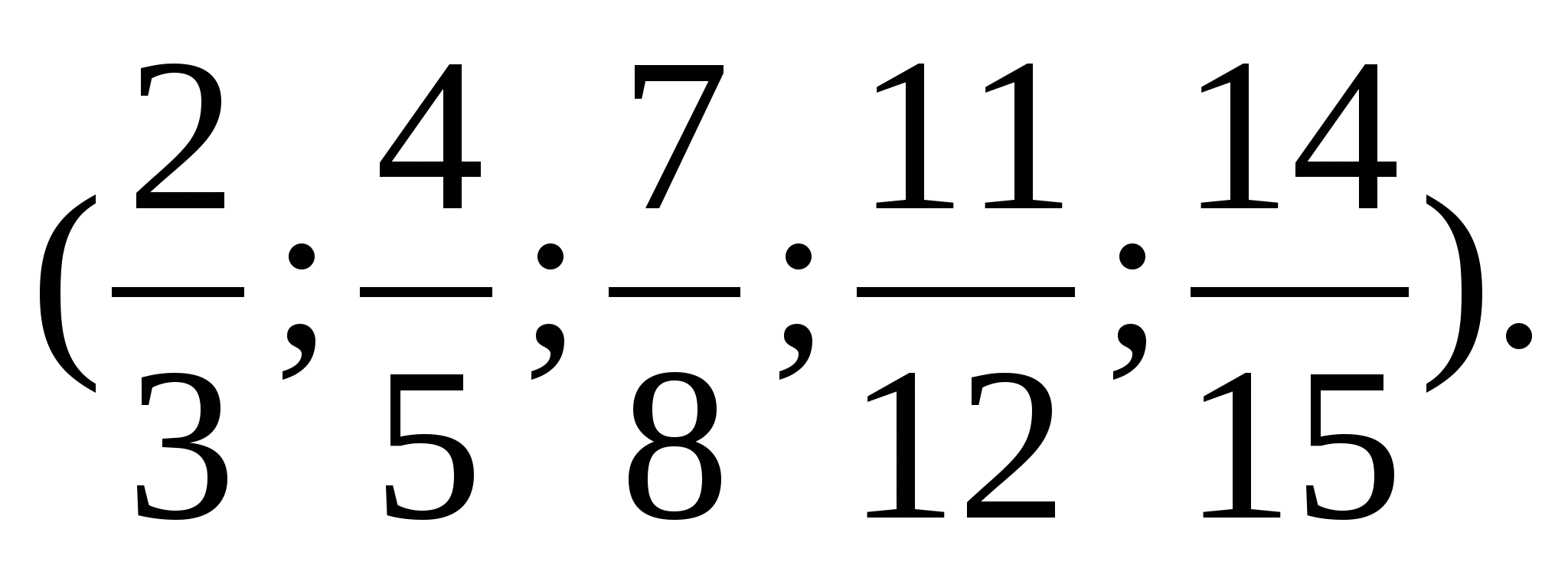
Якими по відношенню до одиниці є всі використані нами
дроби?
А як із цих дробів отримати неправильні?
Якими вони будуть в порівнянні з 1?
Сформулюйте правило порівняння правильних та неправильних дробів.
Наведіть дроби останнього ряду до найменшого спільному знаменникуі
запишіть їх у порядку зменшення. 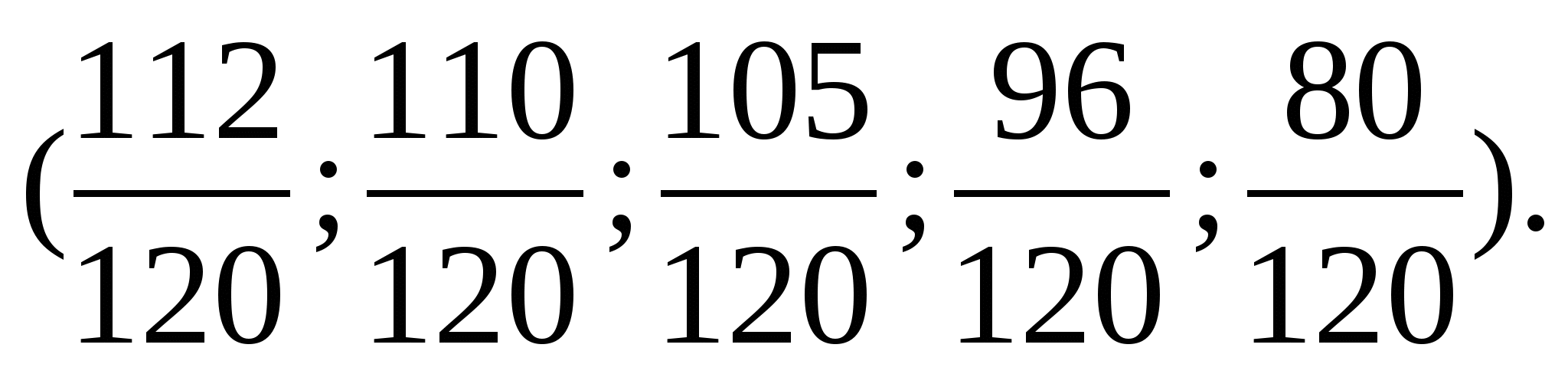
Сформулюйте правило порівняння, яке Ви застосували у цьому випадку.
Який із цих дробів лежатиме на числовому промені правіше за всіх, який –
ліворуч?
Сформулюйте правило порівняння дробів за допомогою числового променя.
Отже, які методи порівняння звичайних дробів ми з Вами повторили?
(Фіксую на античному посудині названі способи порівняння).
3. Постановка навчальної задачі.
Завдання:
Порівняйте дроби та дайте пояснення отриманому результату:
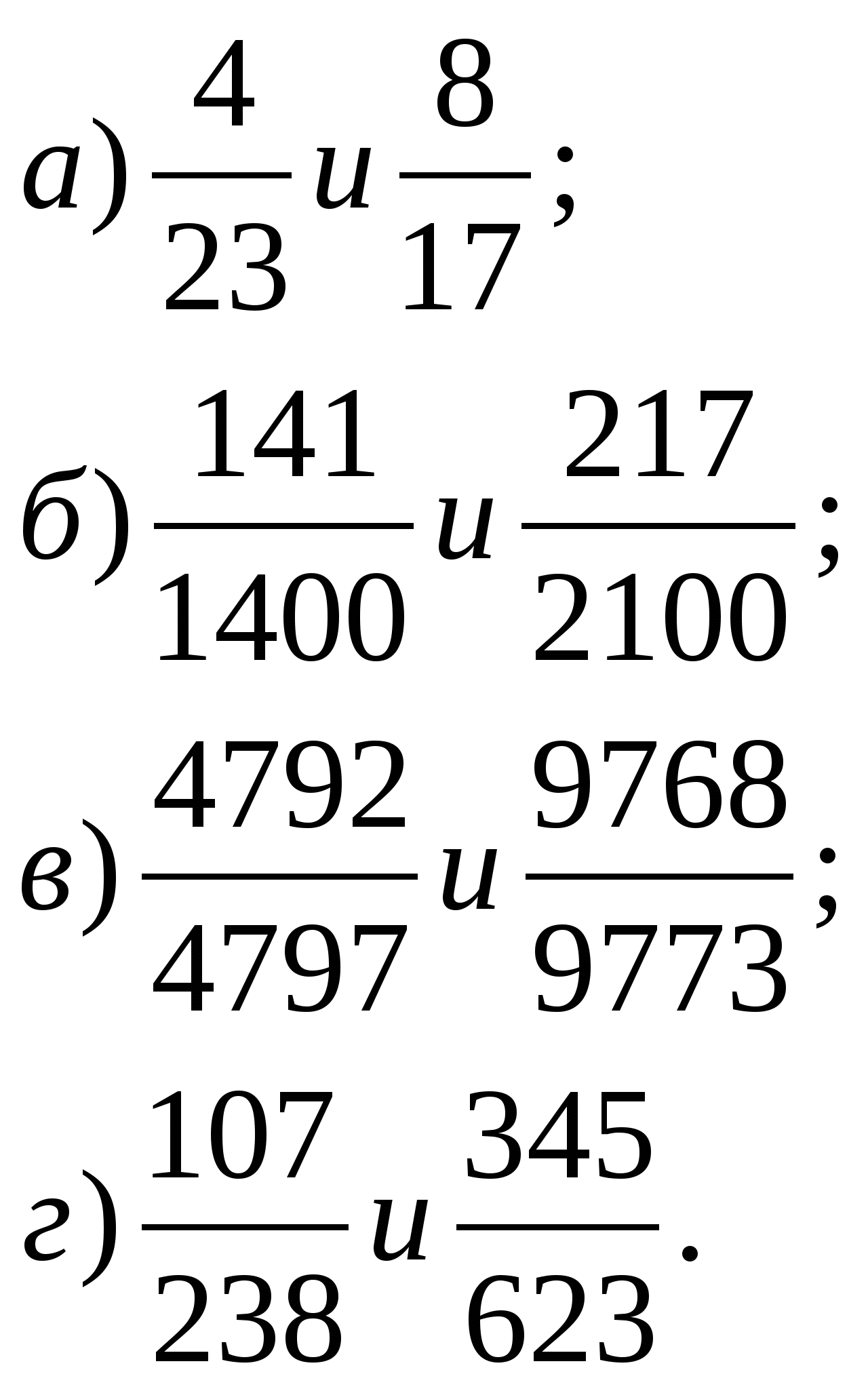
(Виконують завдання індивідуально у зошитах протягом 3 – 4 хвилин).
Після закінчення часу перевіряємо виконану роботу з промовленням способу порівняння.
На якій парі дробів виникла скрута і чому?
То яке ж постало перед нами завдання?
А як би ви сформулювали тему нашого уроку?
Із запропонованих варіантів вибираємо, підходяще і записуємо в зошитах.
(Можливі варіанти: Додаткові, хитрі, нові і т.д.
методи порівняння звичайних дробів.)
Повторіть ще раз поставлене на сьогоднішній урок завдання.
4. "Відкриття" нового знання.
Щоб перевірити, наскільки Ви мали рацію у своїх припущеннях у 3 та 4 прикладах, Вам пропонується виконати наступні завдання:
Уявіть приватні 8: 12; 12: 16; 16: 20; 20: 24 у вигляді нескоротних дробів. 
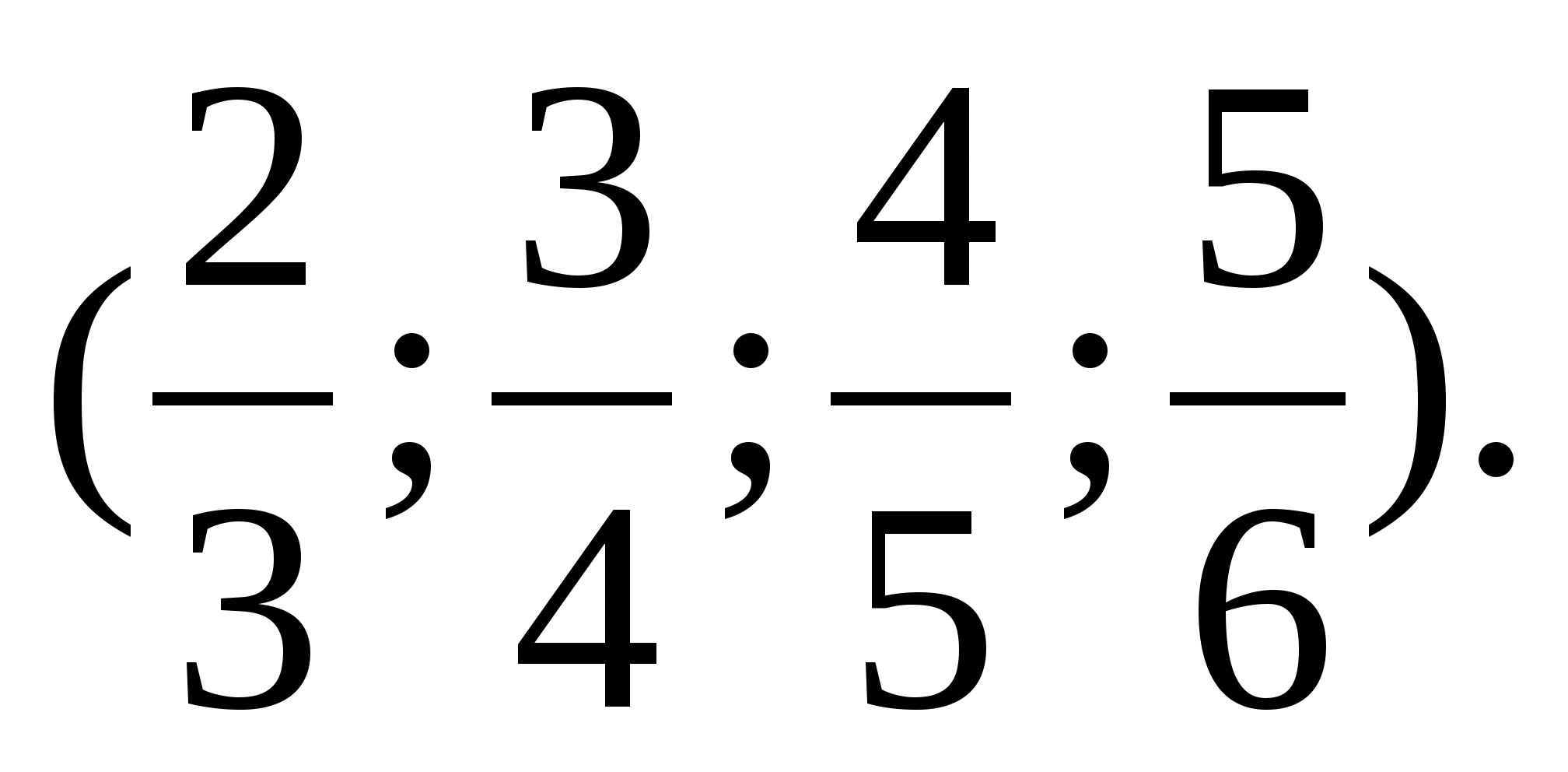
Що цікавого Ви помітили у отриманому ряді дробів?
Назвіть три дроби. 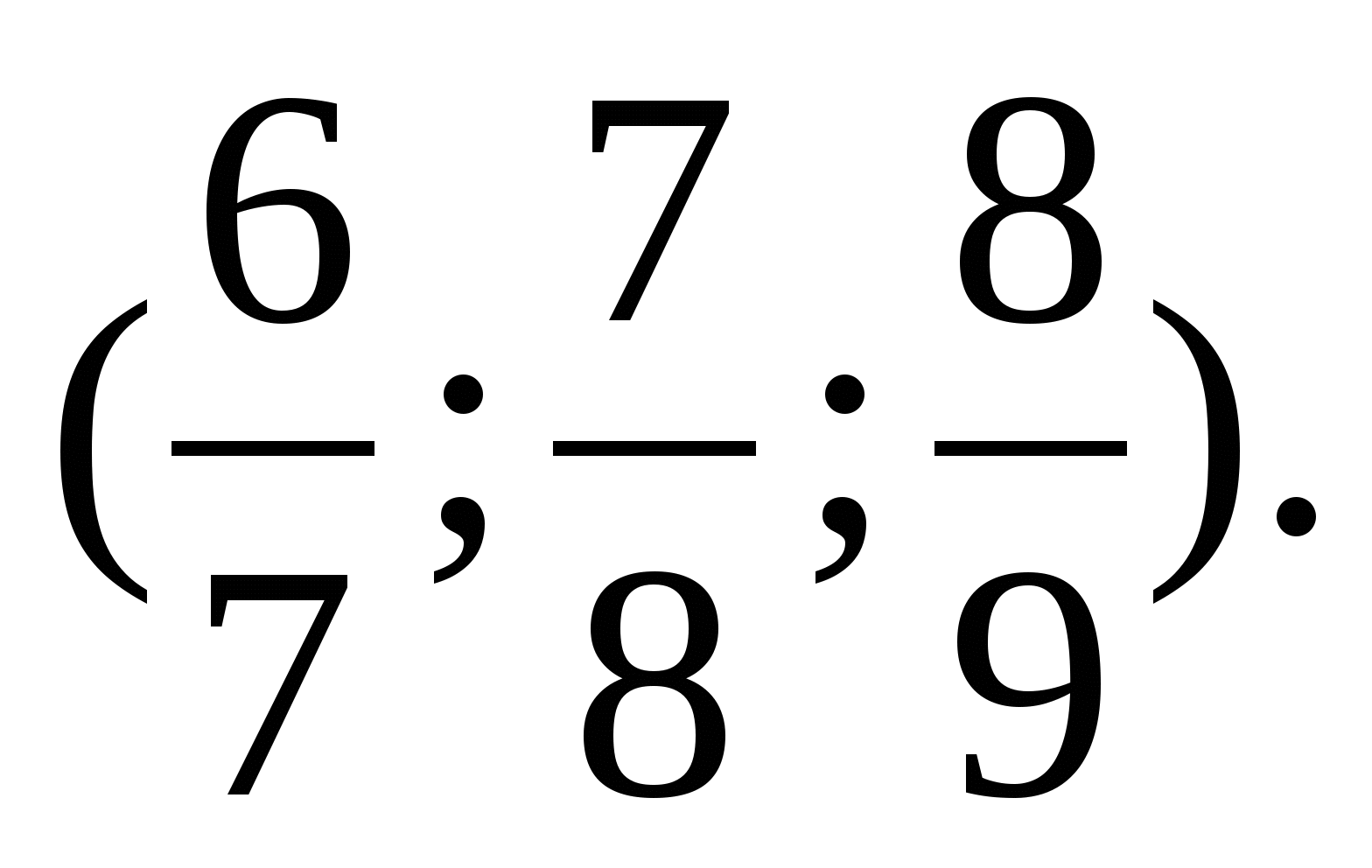
Який дріб стоїть на 34 місці? А на 999? 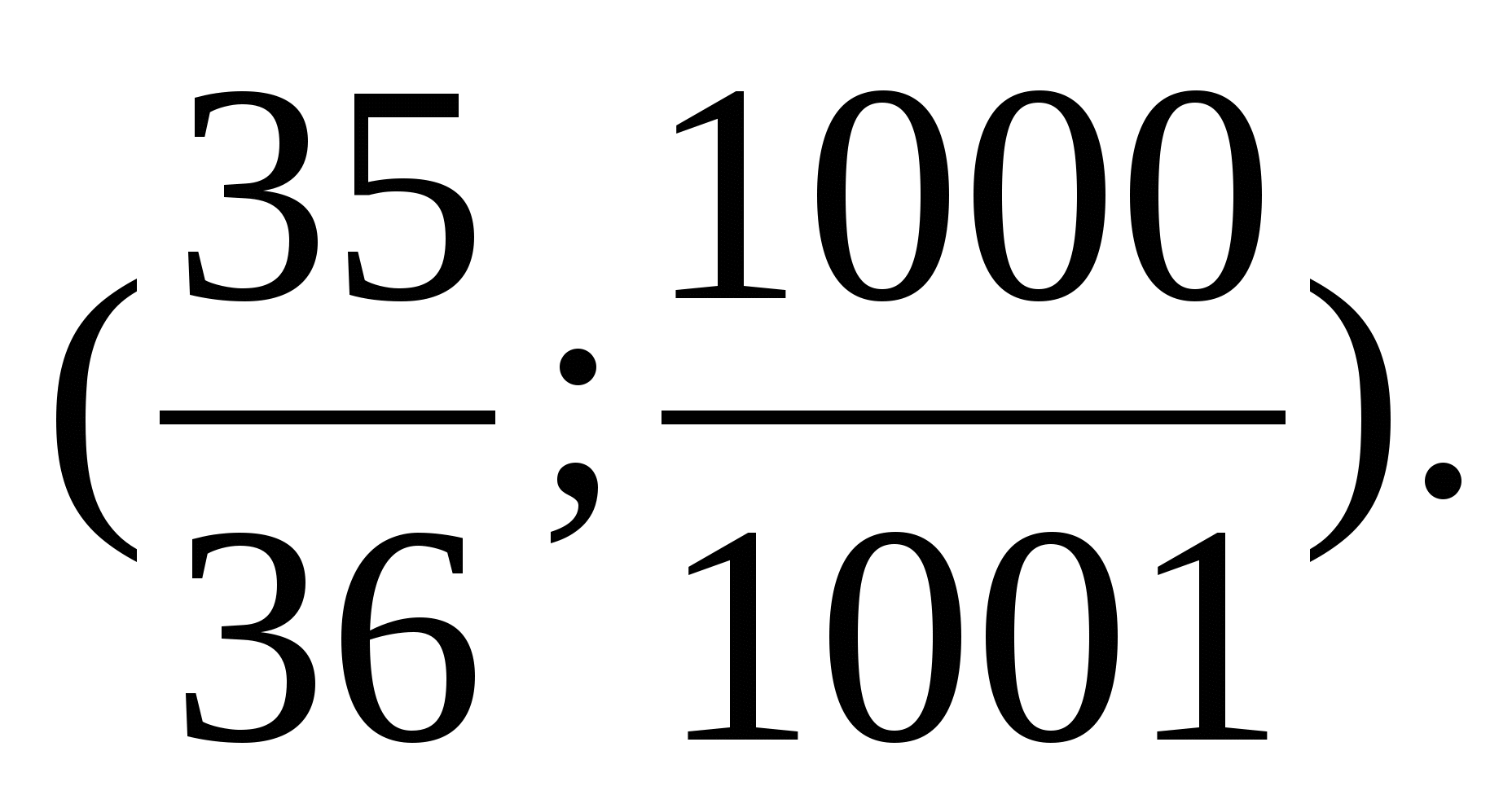
Припустіть, у якому порядку розташовані дроби у цьому ряду і чому?
Тоді який знак порівняння Ви поставили б між дробами 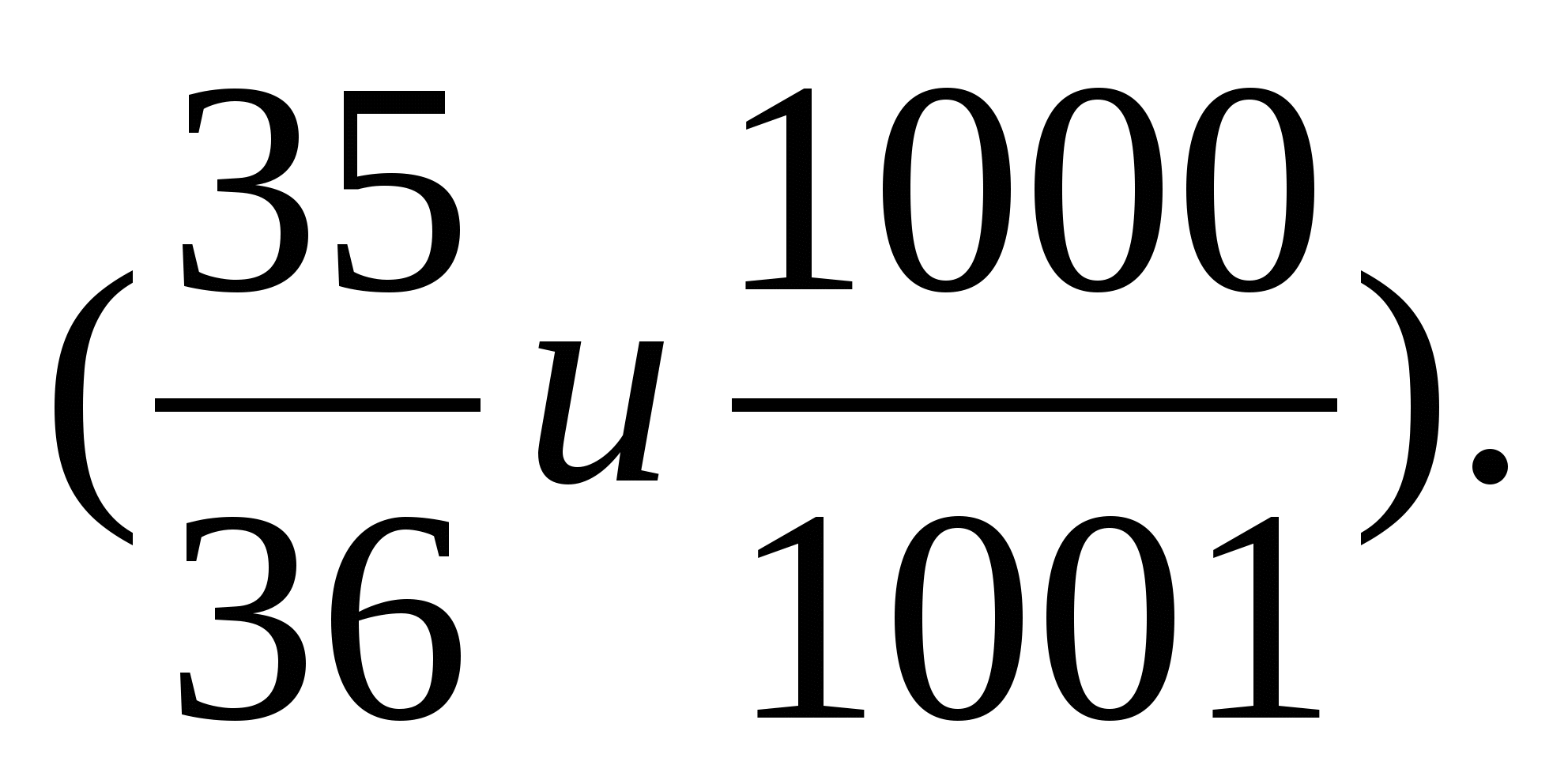 ?
?
А як довести висловлене припущення?
Доповніть кожен із дробів до 1. 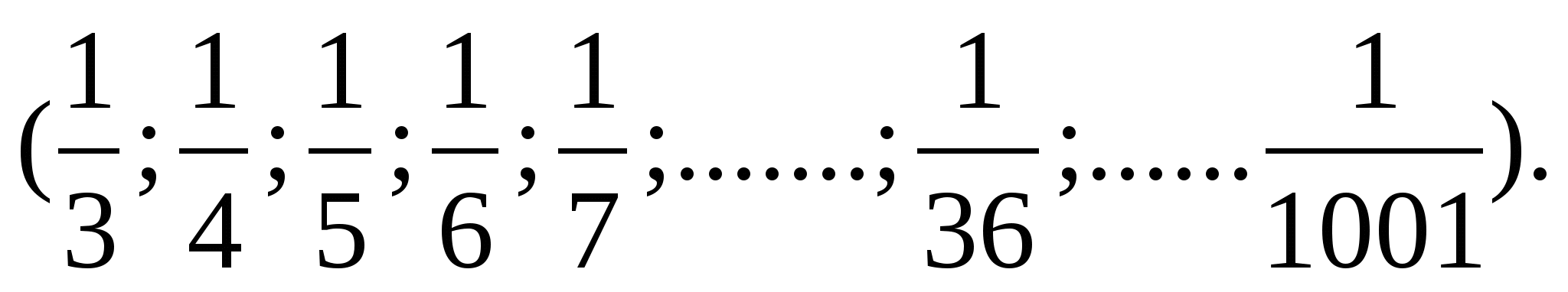
А чи легко порівняти отримані порівняння?
Порівняйте.
Правильно, чи було наше припущення щодо дробів 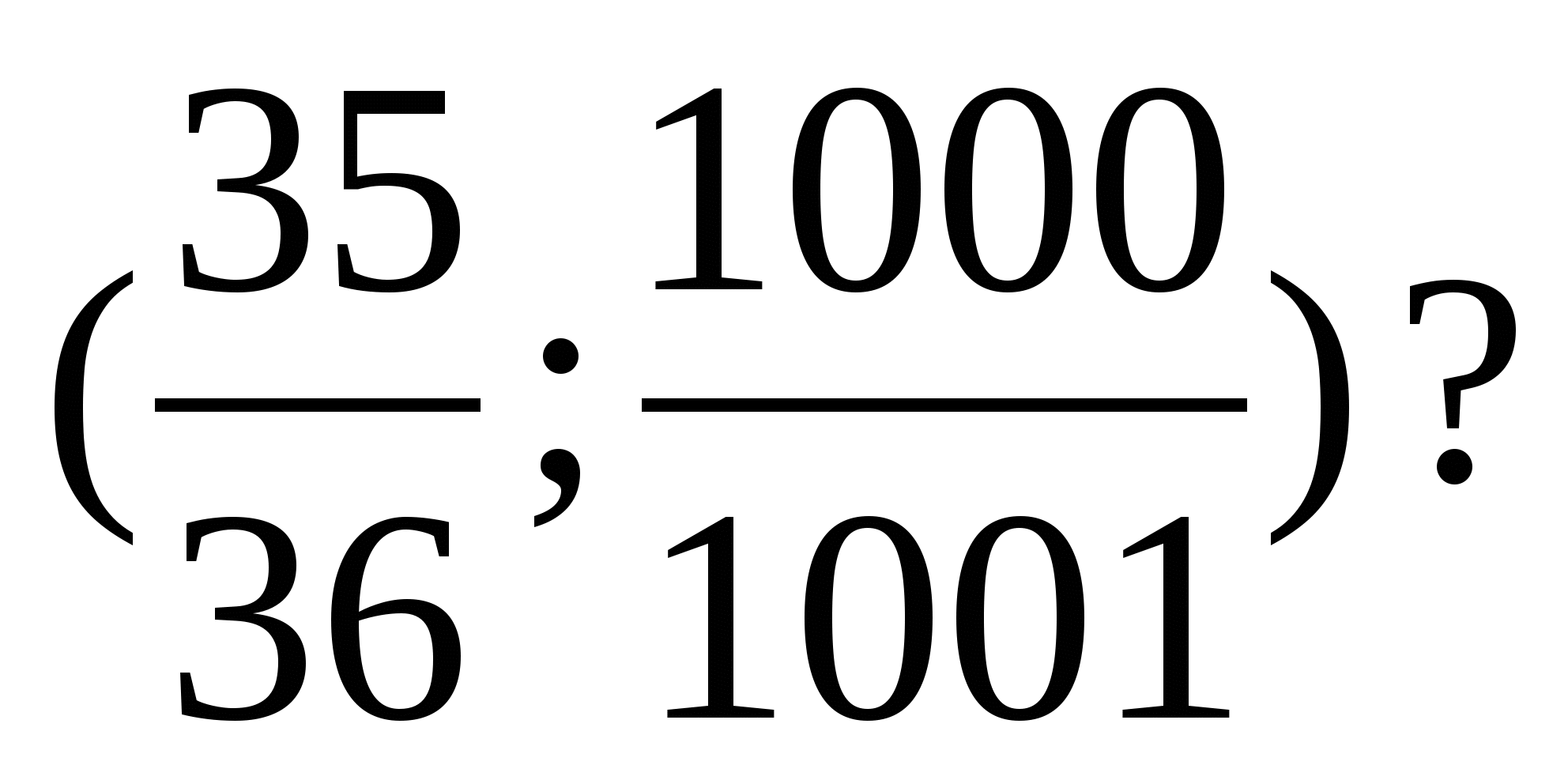
Чи легко тепер порівняти дроби з пункту в)?
Порівняйте.
Як Ви назвали отриманий спосіб порівняння?
Проговоріть ще раз суть способу порівняння дробів доповненням до 1.
А чи можна, використовуючи спосіб доповнення до 1, порівняти дроби 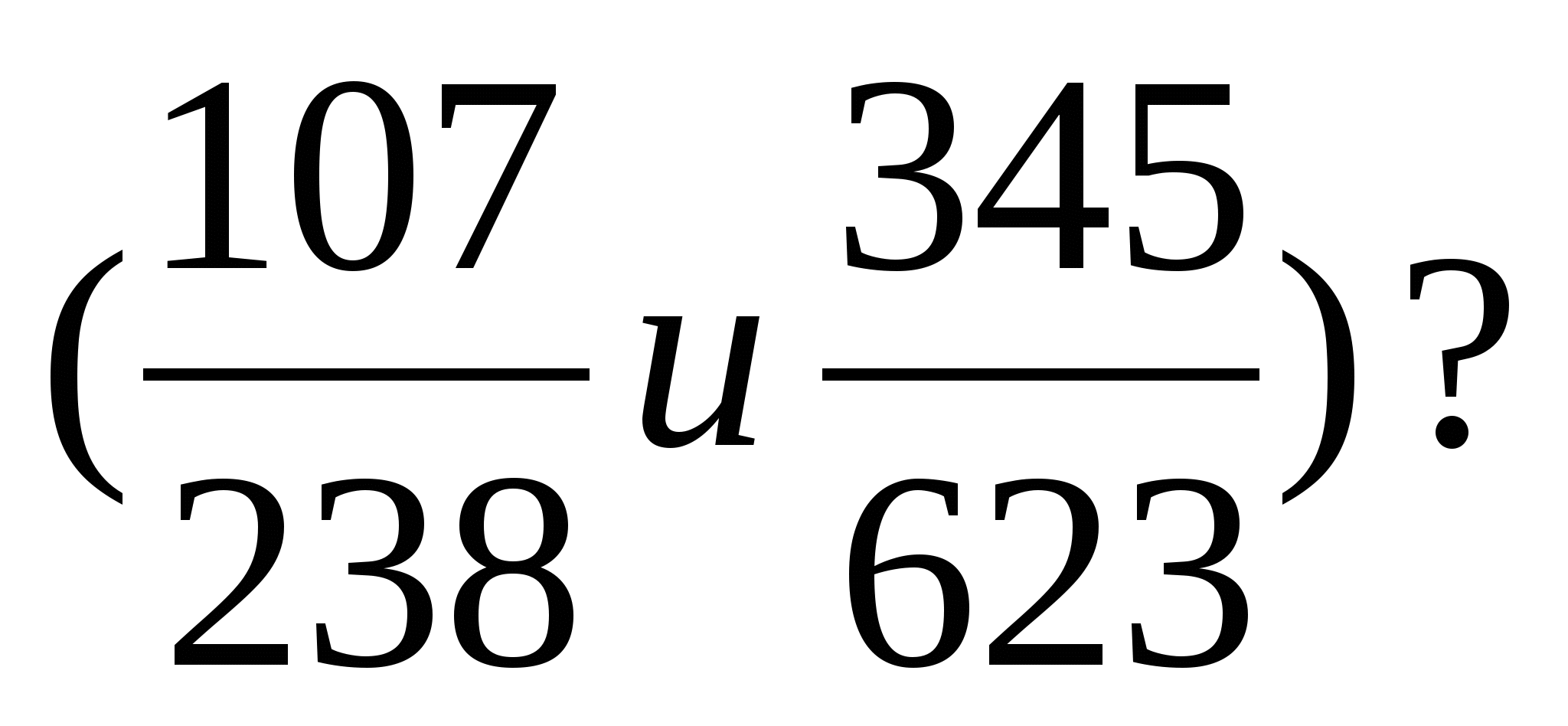
А може у когось із Вас є гіпотеза, як це зробити чи припущення, в якому напрямку нам слід рухатися?
Тоді я пропоную Вам попрацювати в парах над наступним завданням, яке я сподіваюся, допоможе знайти вихід із цього скрутного становища.
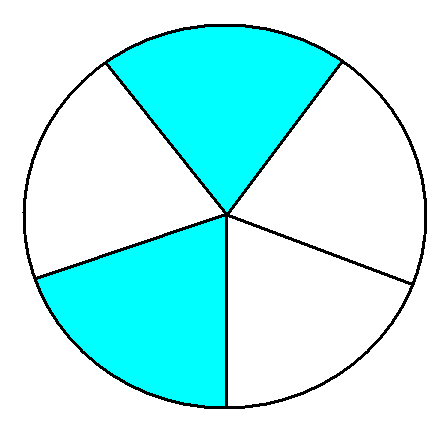
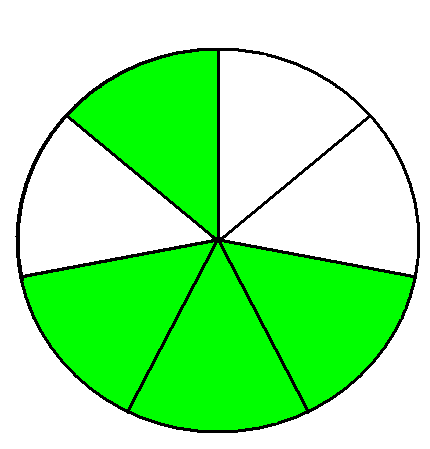
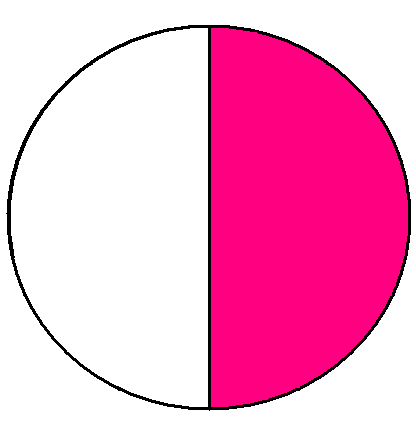
У Вас на партах лежать малюнки, за якими Вам треба:
1. Записати зображені на малюнках дроби.
2. Скласти з них усі можливі нерівності.
3. Результат роботи подати на дошці під відповідним малюнком.
(лунають 4 види карток). (Додаток 1)
ВІДПОВІДІ:
До - 1
До - 2
До - 3
До - 4
Дроби
Нерівність
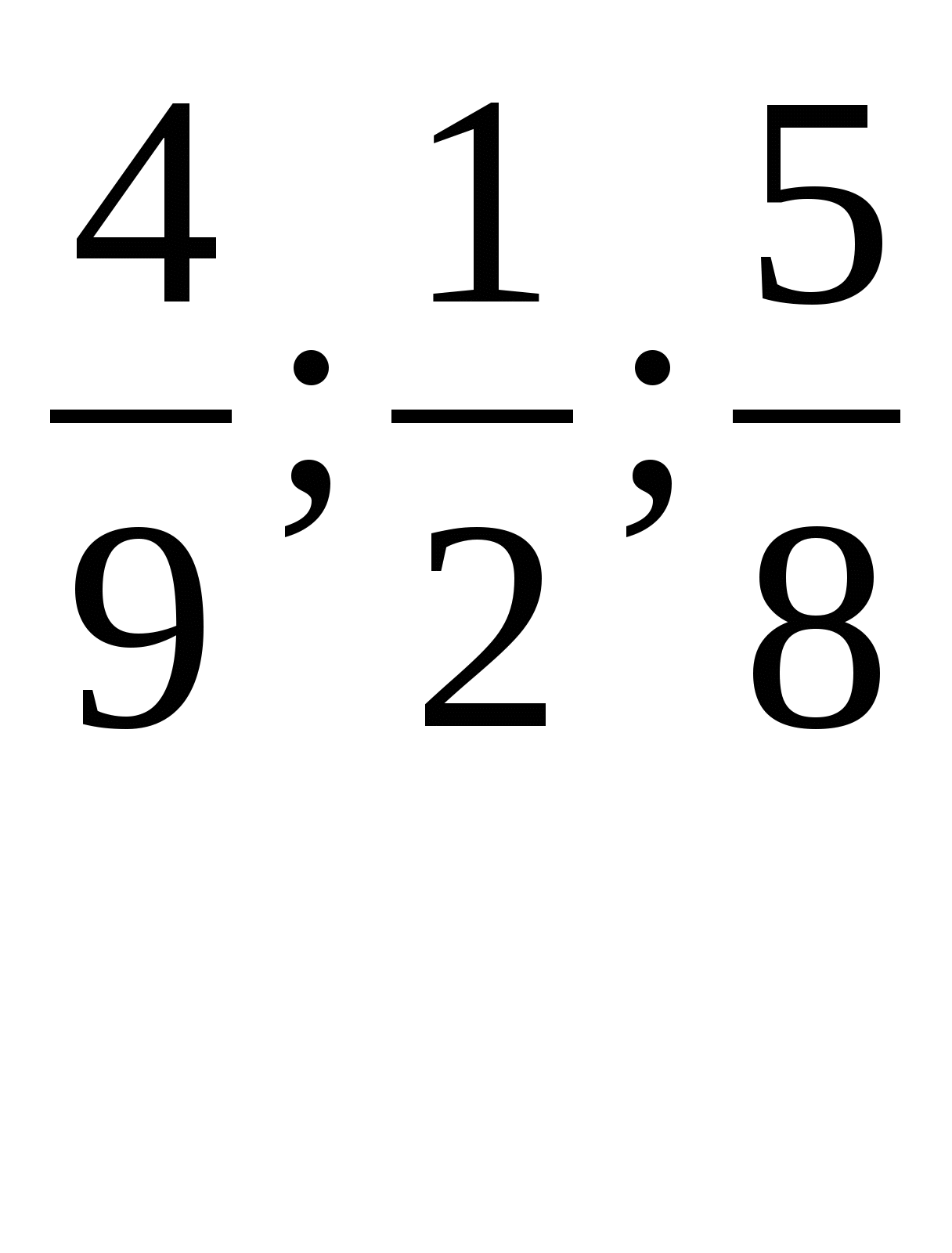
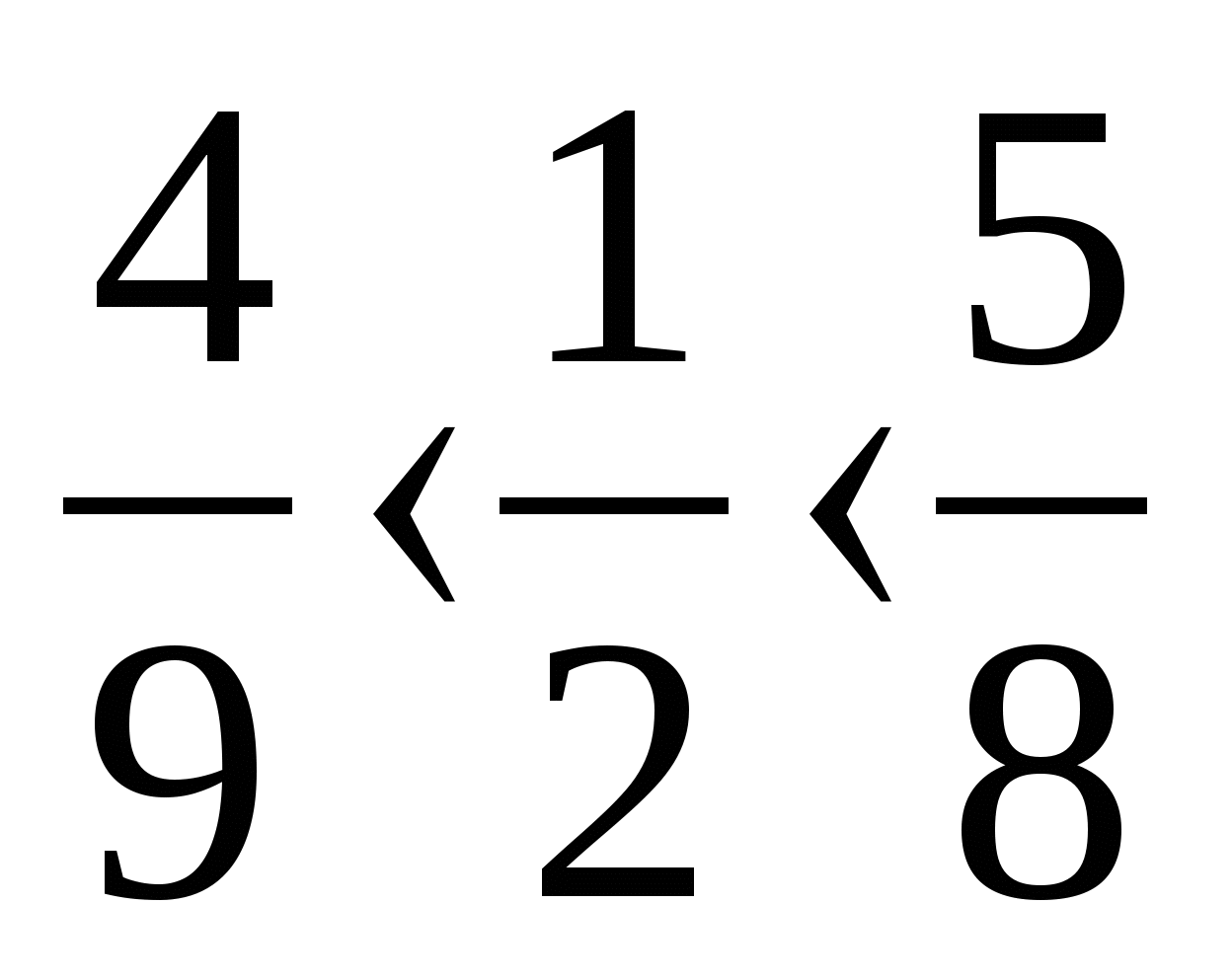
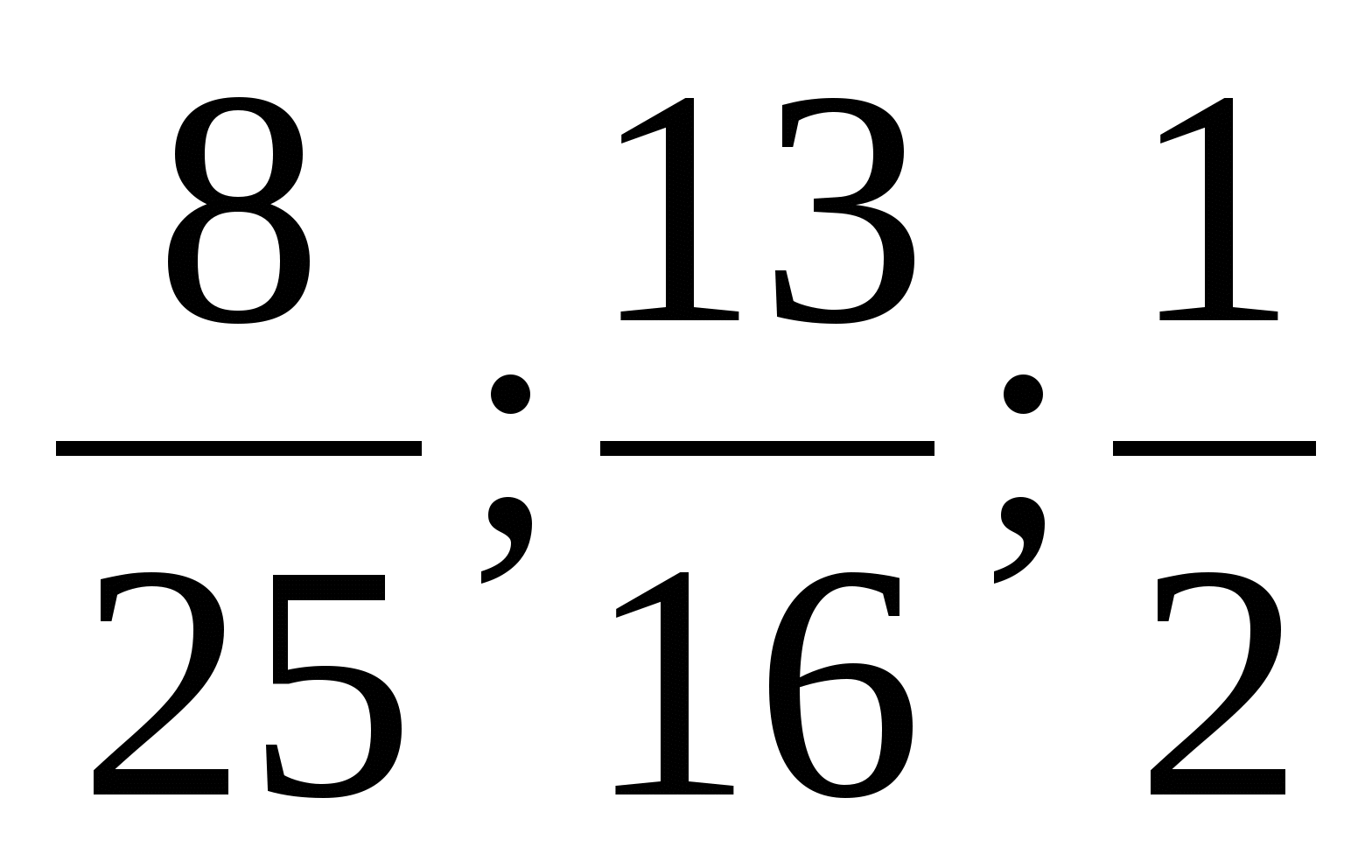
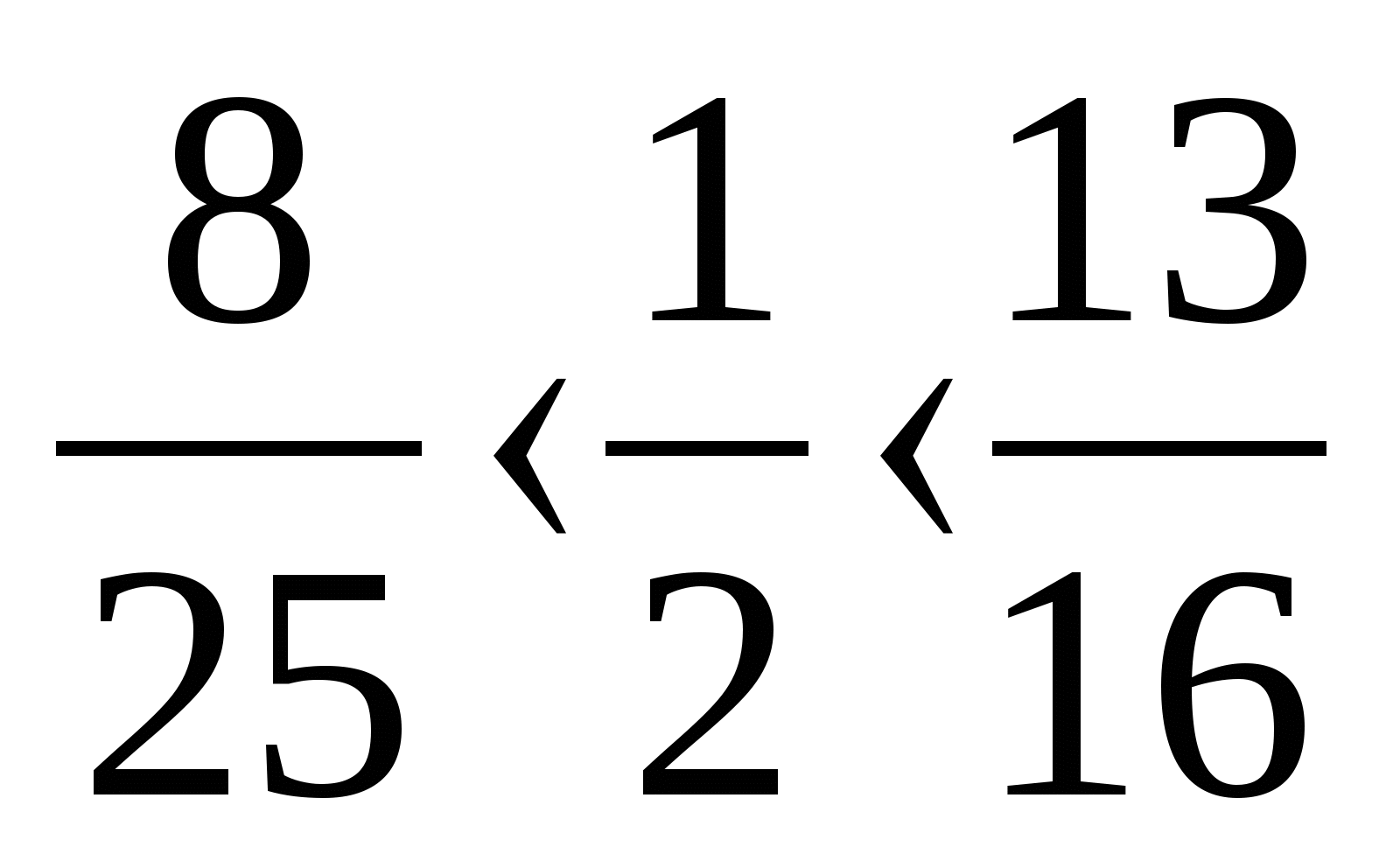
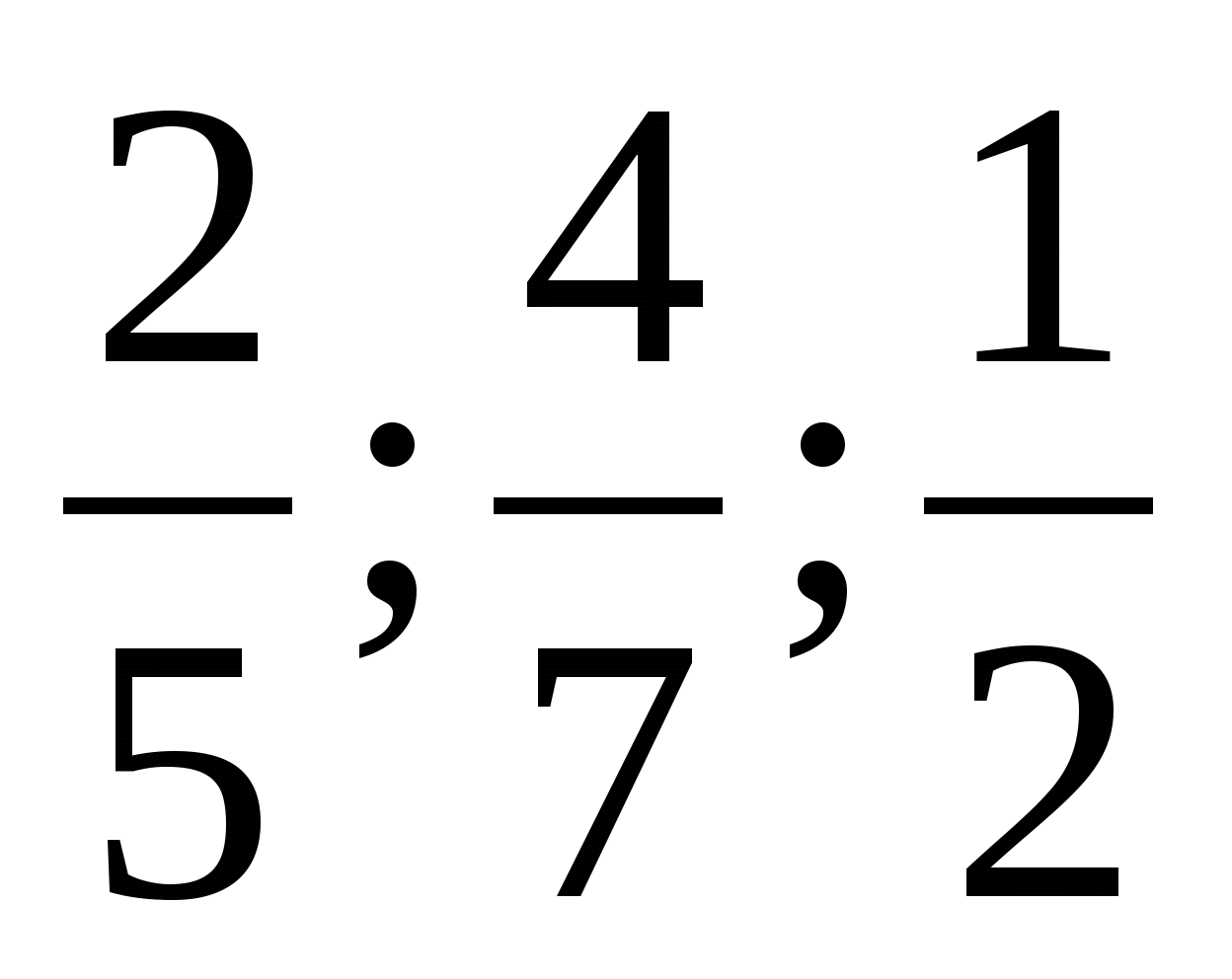
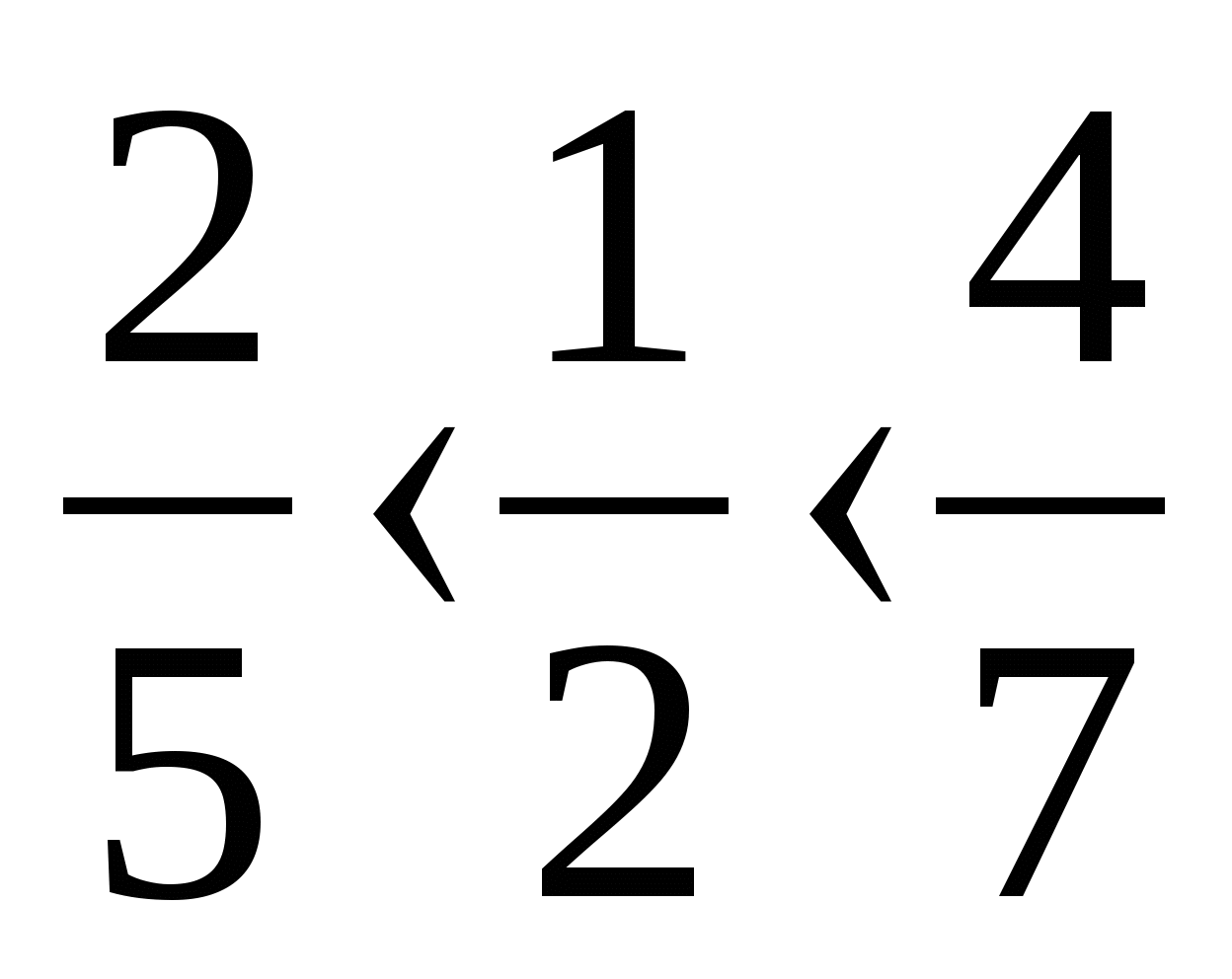
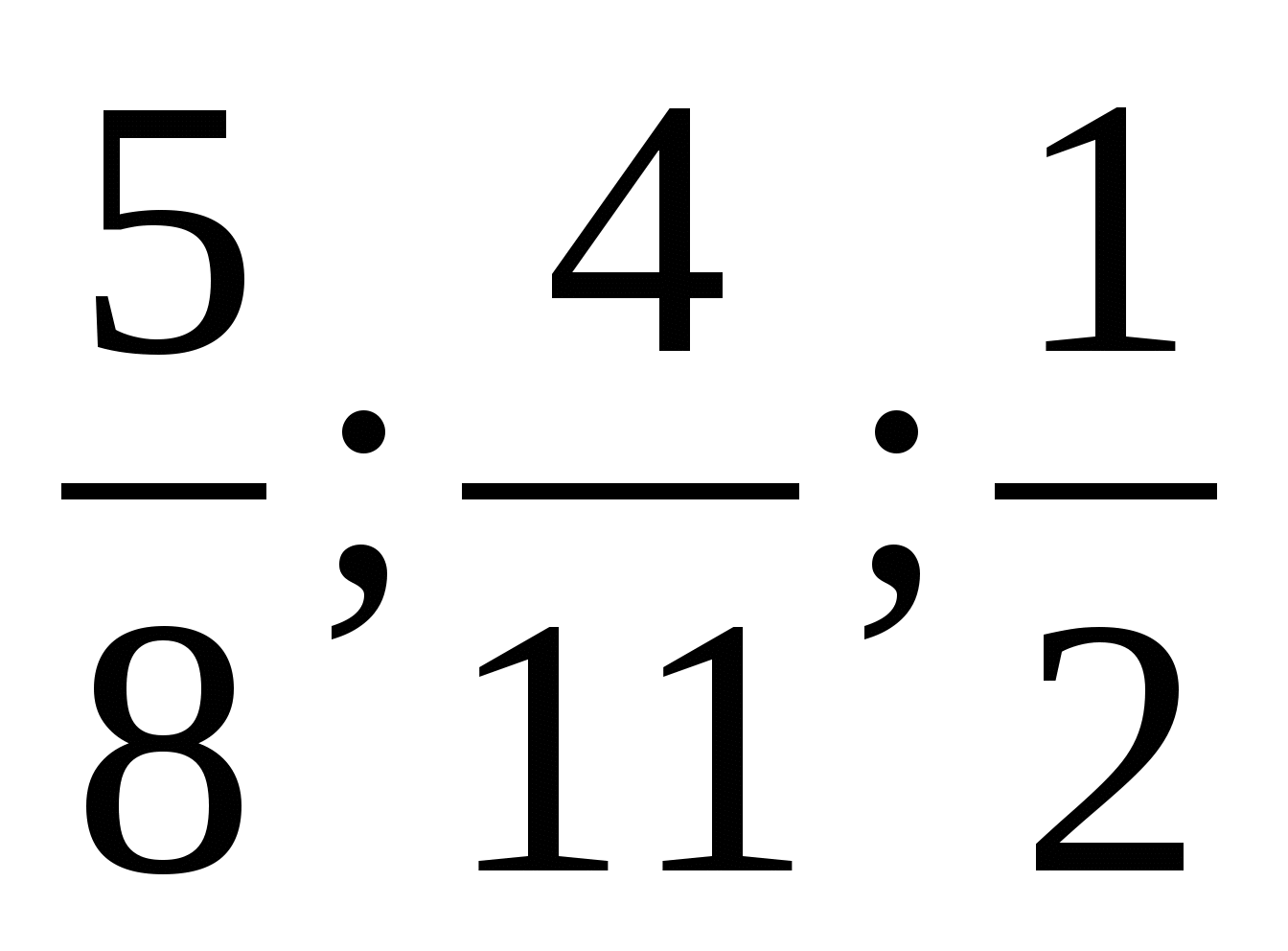
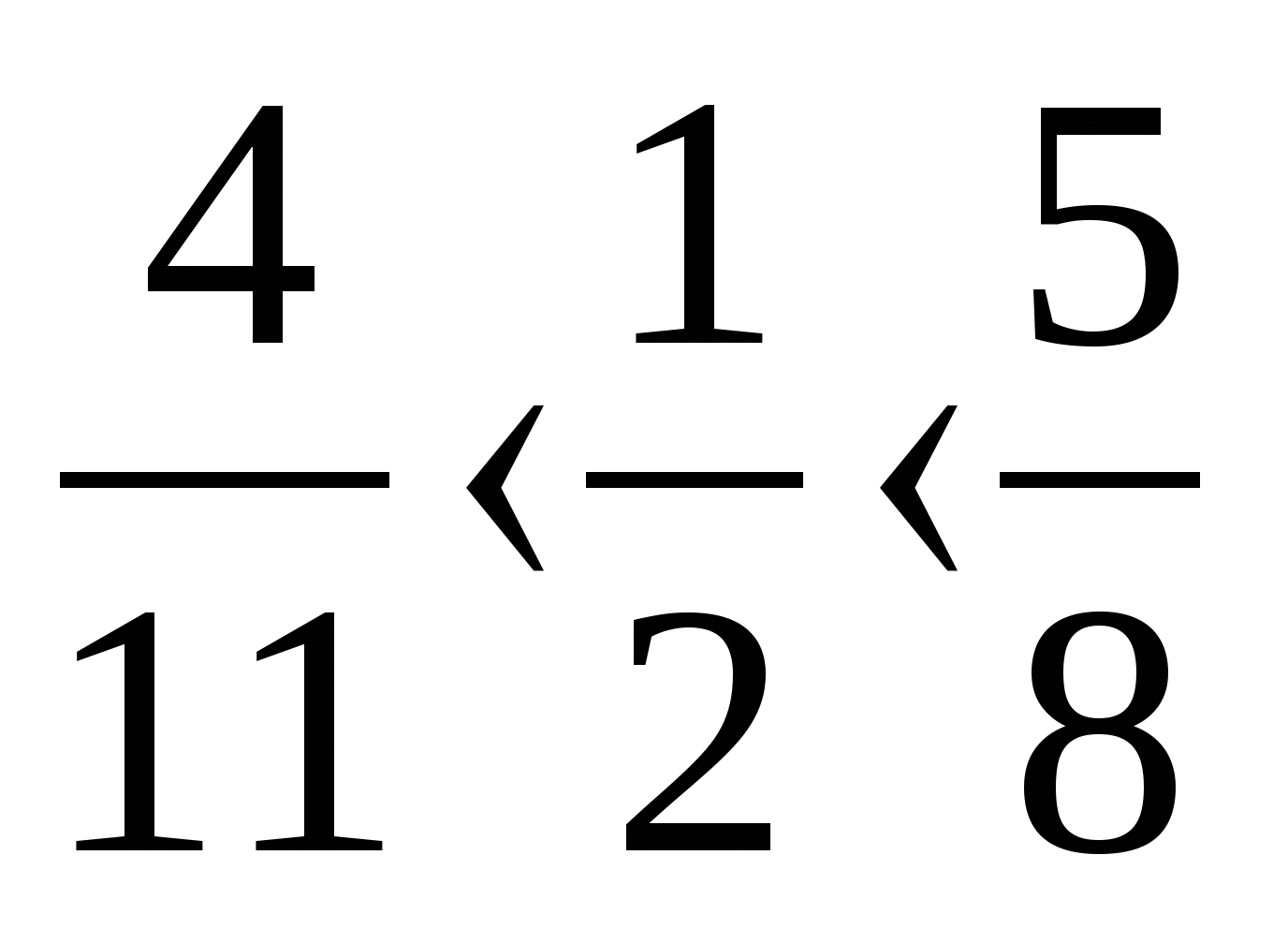
Що спільного Ви помітили у представлених порівняннях? (1/2).
Проаналізуйте їх та зробіть висновок, з яким числом та як Вам доводилося порівнювати?
А тепер перевірте вірно, чи неправильно було виконано Ваше порівняння останньої пари дробів та поясніть чому?
Яка назва даним способомпорівняння Ви б дали?
Ще раз сформулюйте суть способу порівняння дробів із ½.
Більш загальна назва цього способу – це порівняння дробів із проміжним числом, яке може бути як дробовим, так і цілим, якщо ми маємо справу з неправильними дробами.
Отже, які нові Методи порівняння звичайних дробів ми можемо використовувати під час вирішення завдань порівняння?
(Промовляють назви, а вчитель закріплює їх назви на посудині.)
5. Первинне закріплення у зовнішній промові.
Виконують завдання картки №1 «ланцюжком» з промовленням використаного способу порівняння.
КАРТКА № 1КАРТКА № 1 (Відповіді)
(Закріплення здобутих знань) (Закріплення здобутих знань0
Порівняйте дроби та визначте 1.Порівняйте дроби та визначте
спосіб порівняння: спосіб порівняння:
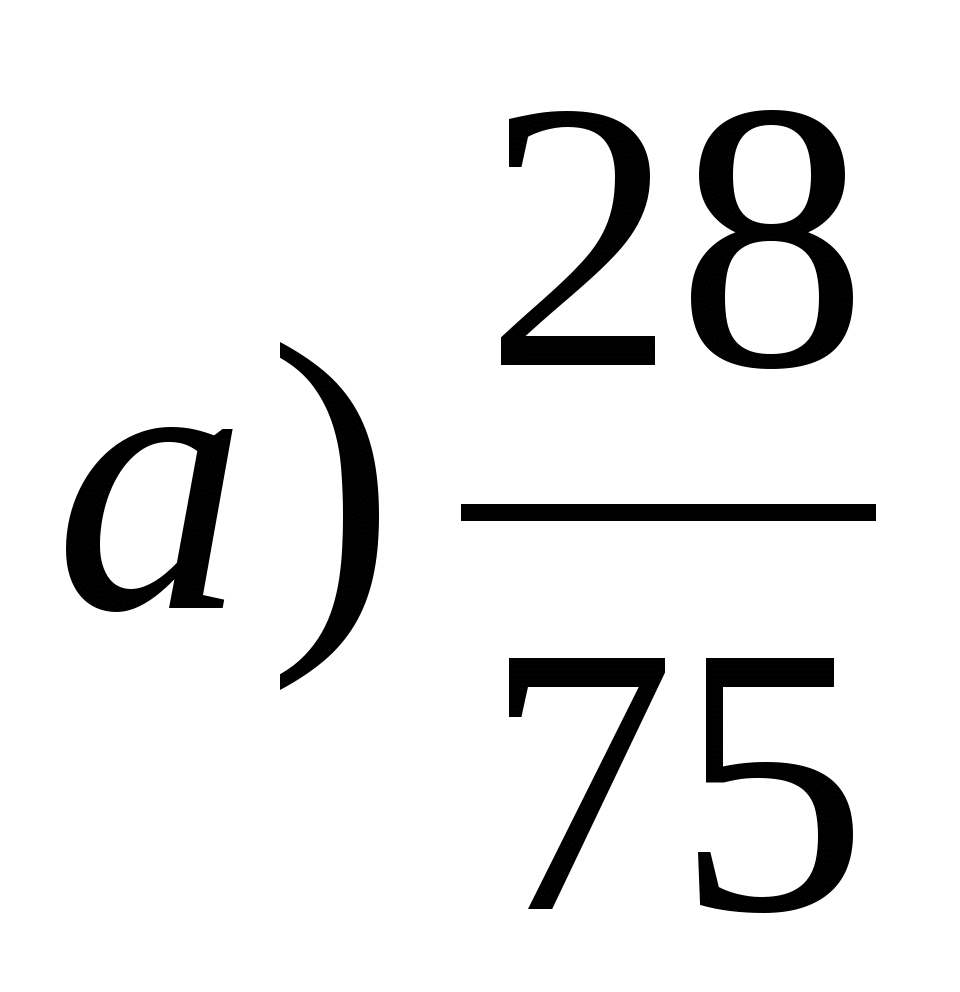 і
і 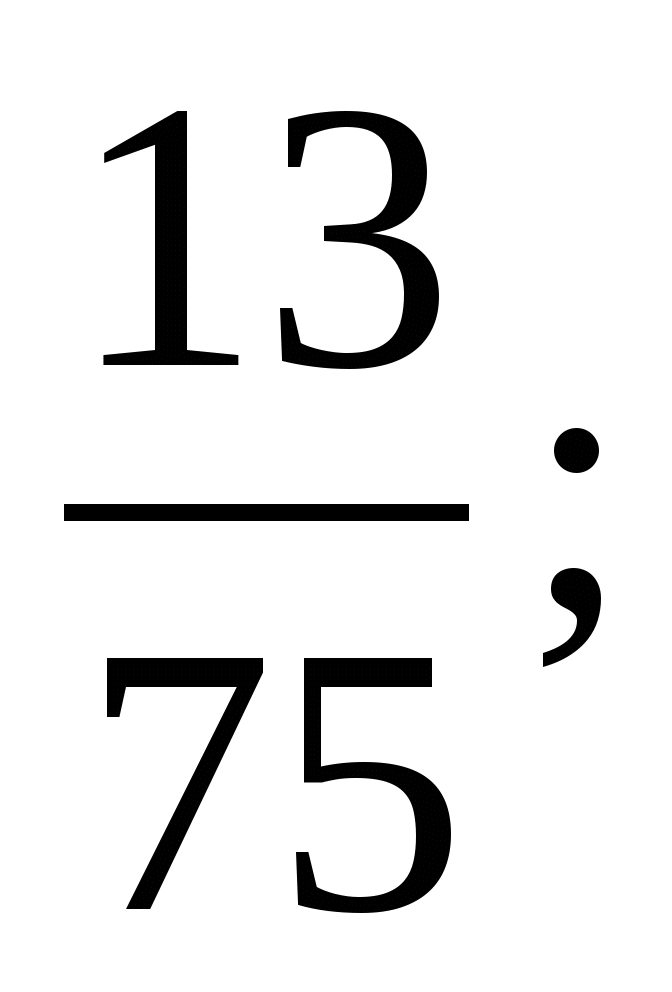
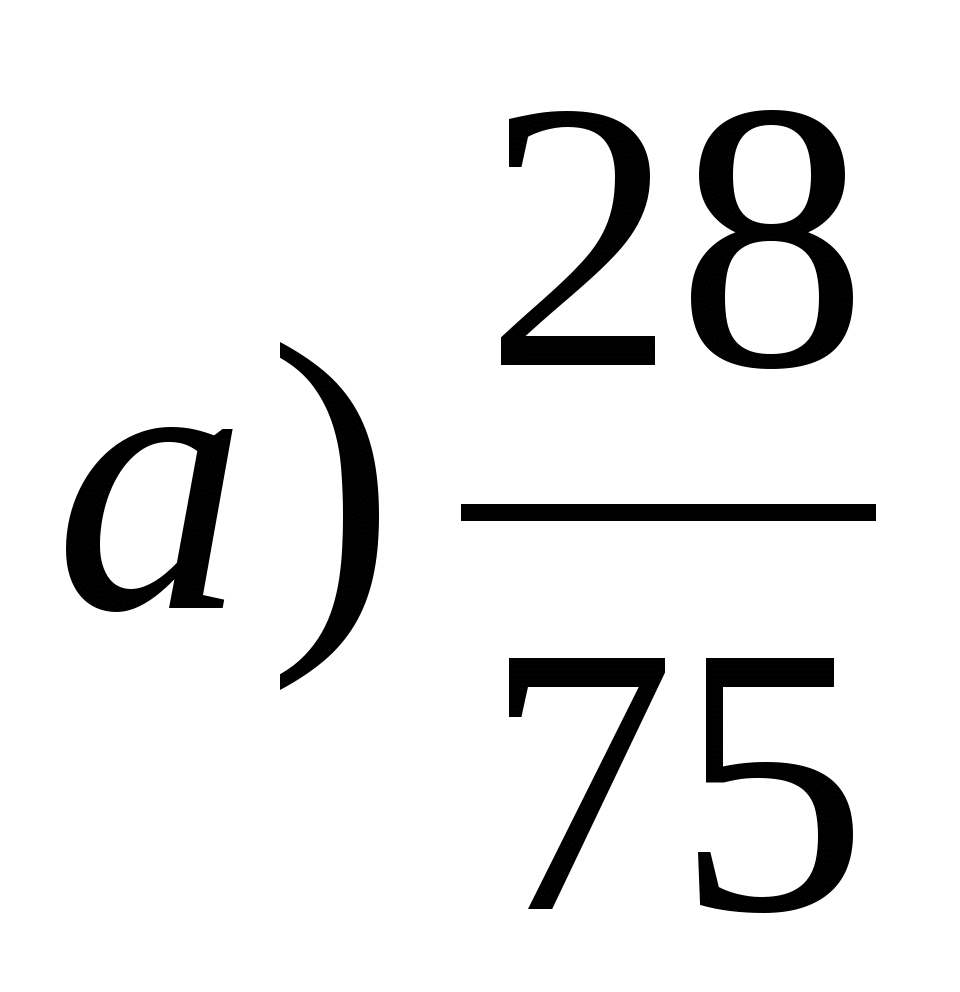 ›
› 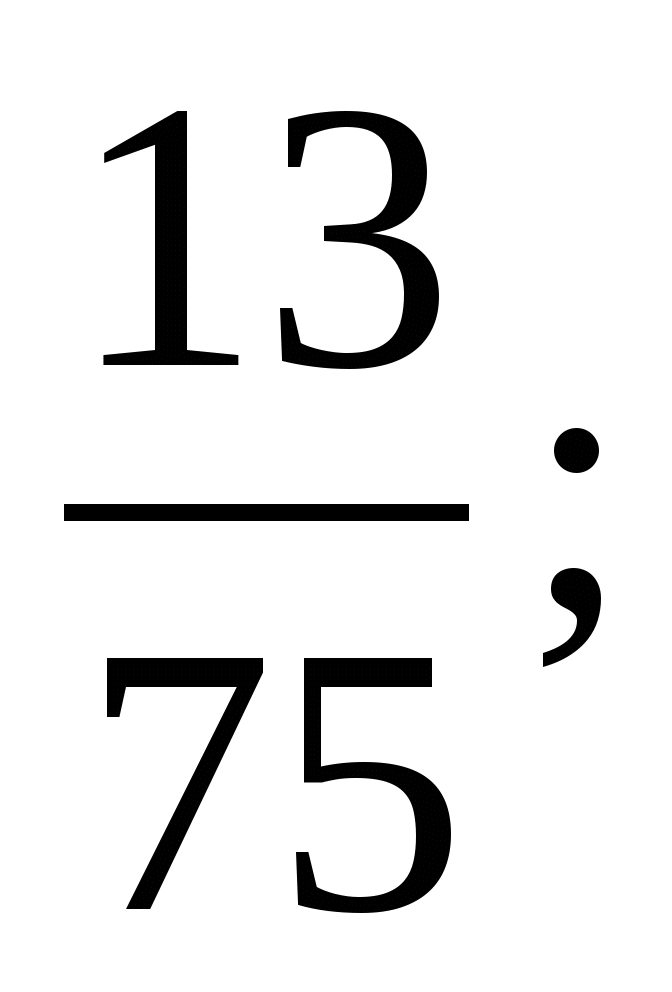 (за знаменником)
(за знаменником)
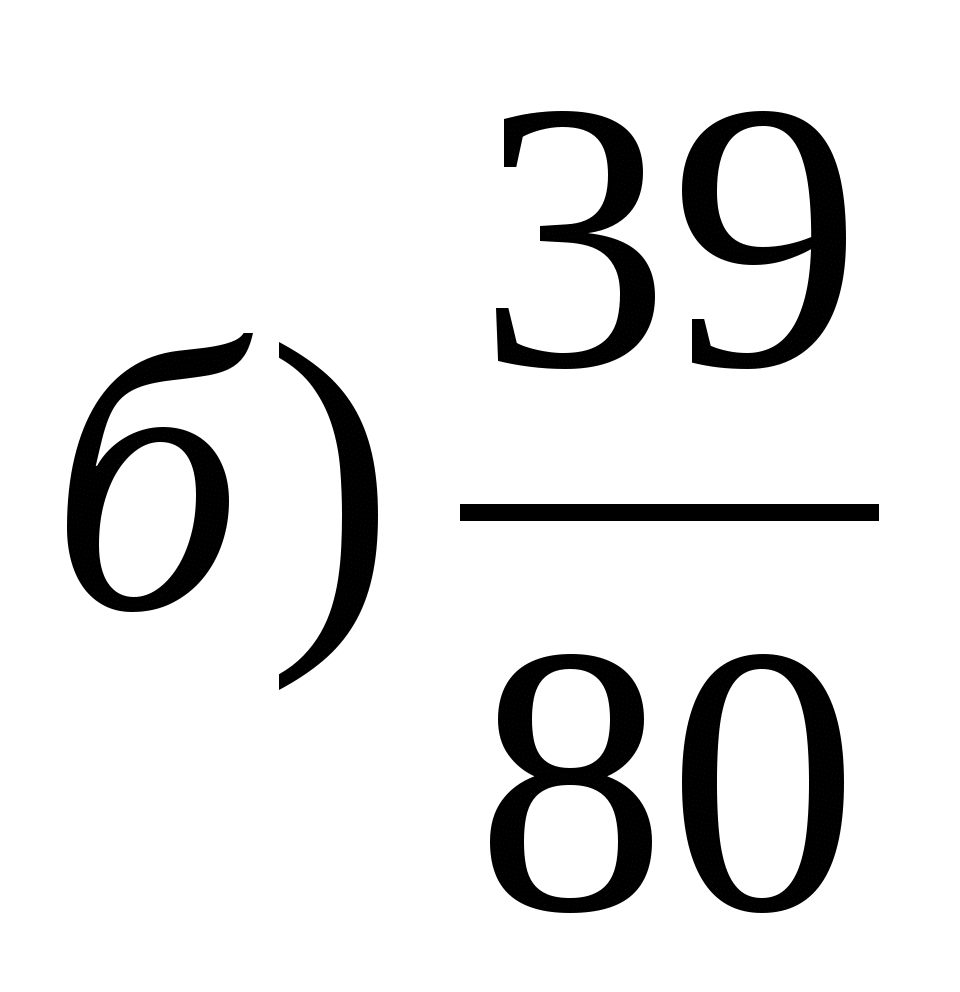 і
і 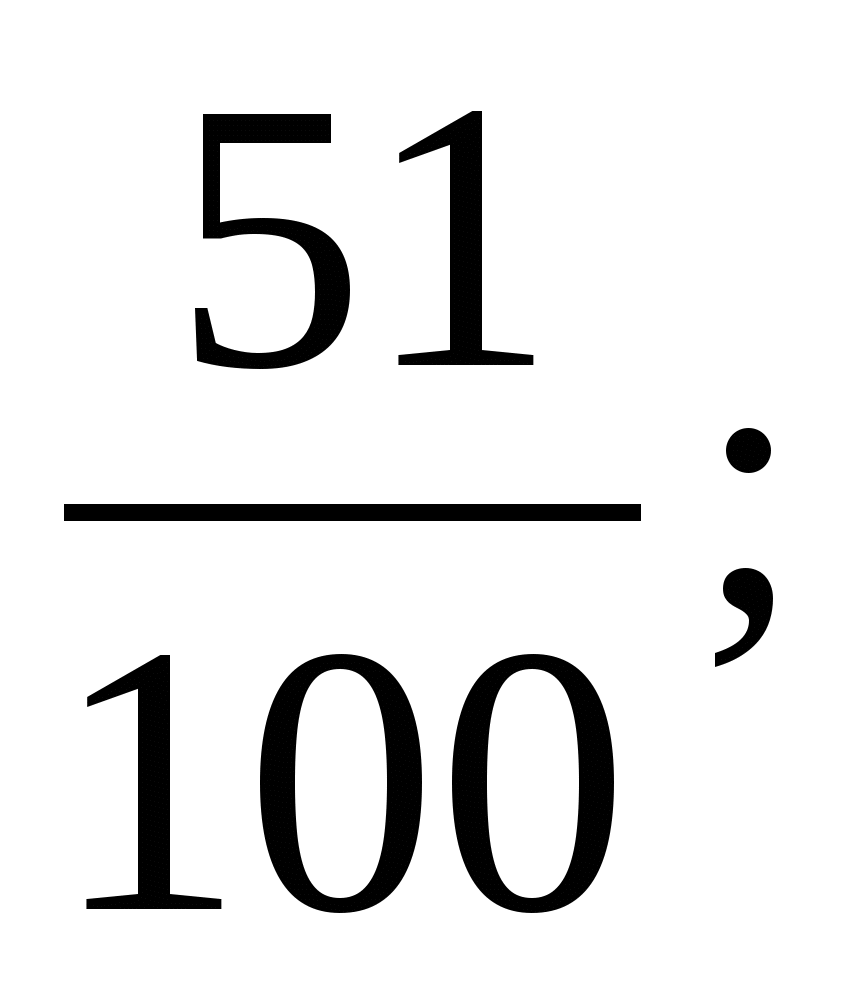
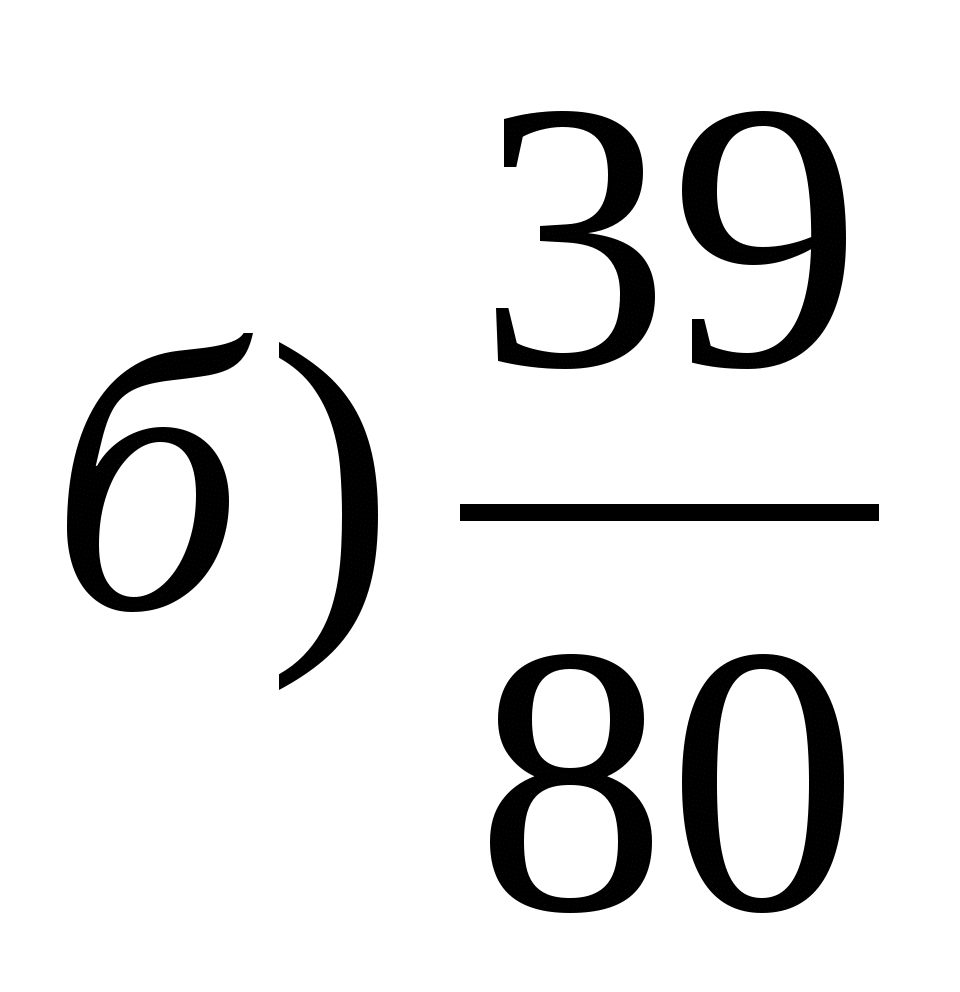 ‹
‹ 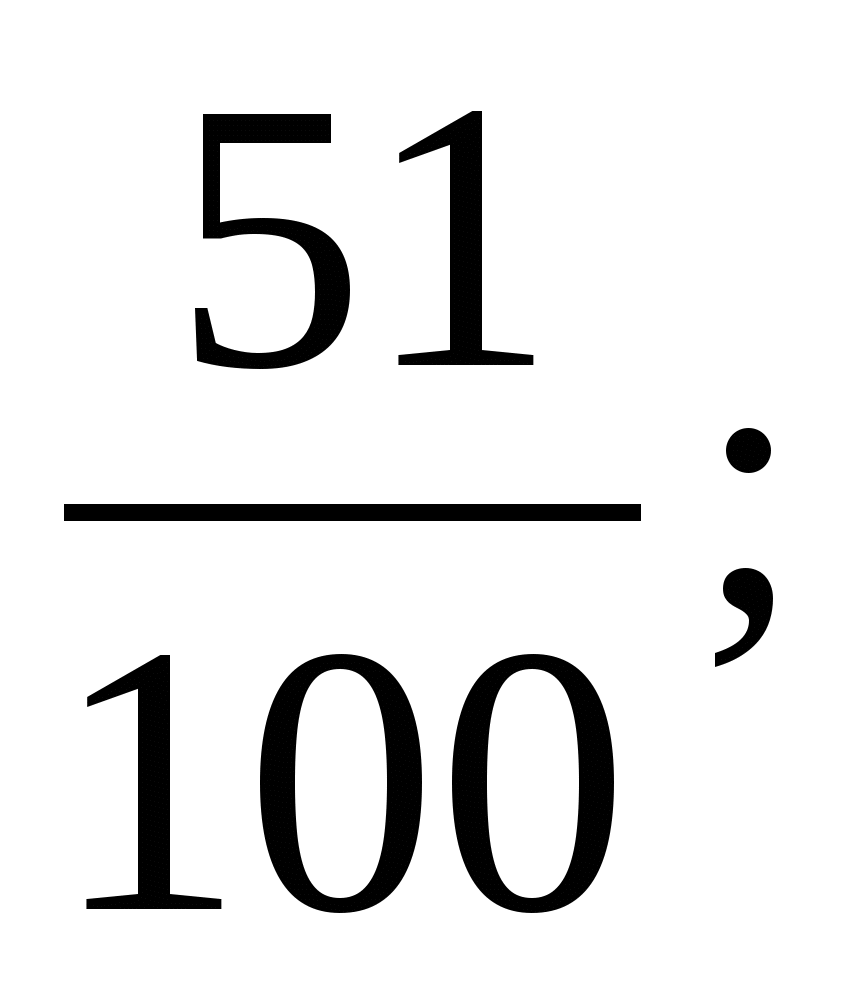 (порівняння з ½)
(порівняння з ½)
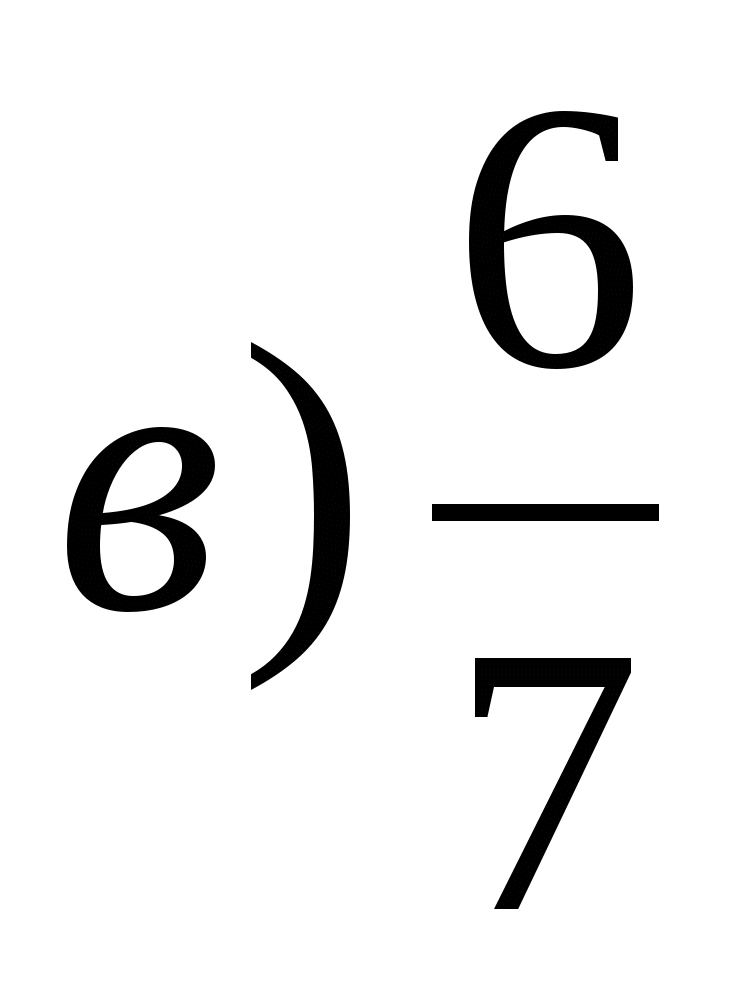 і
і 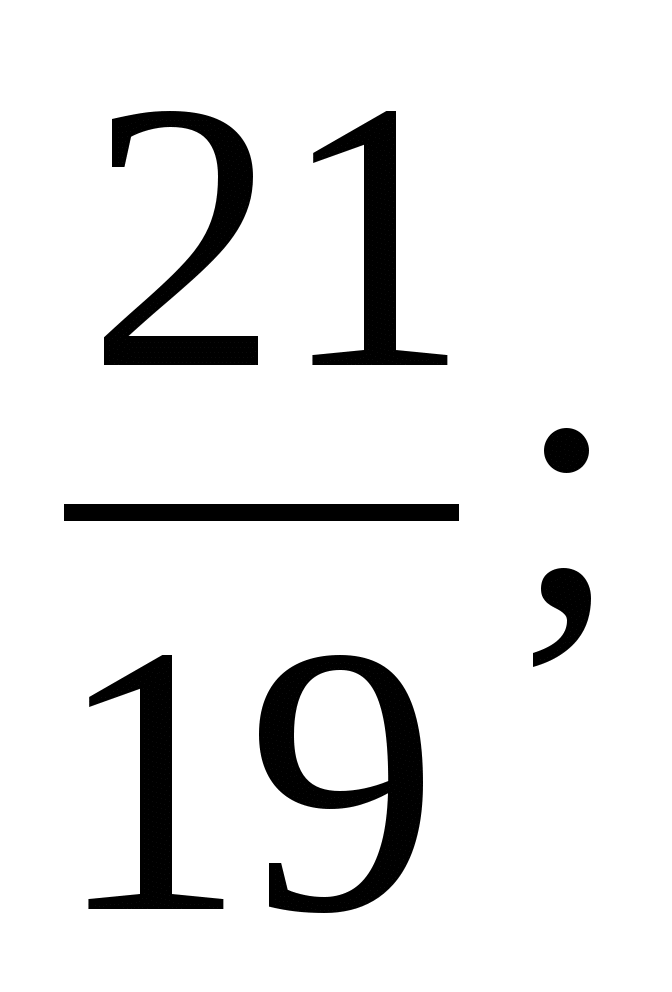
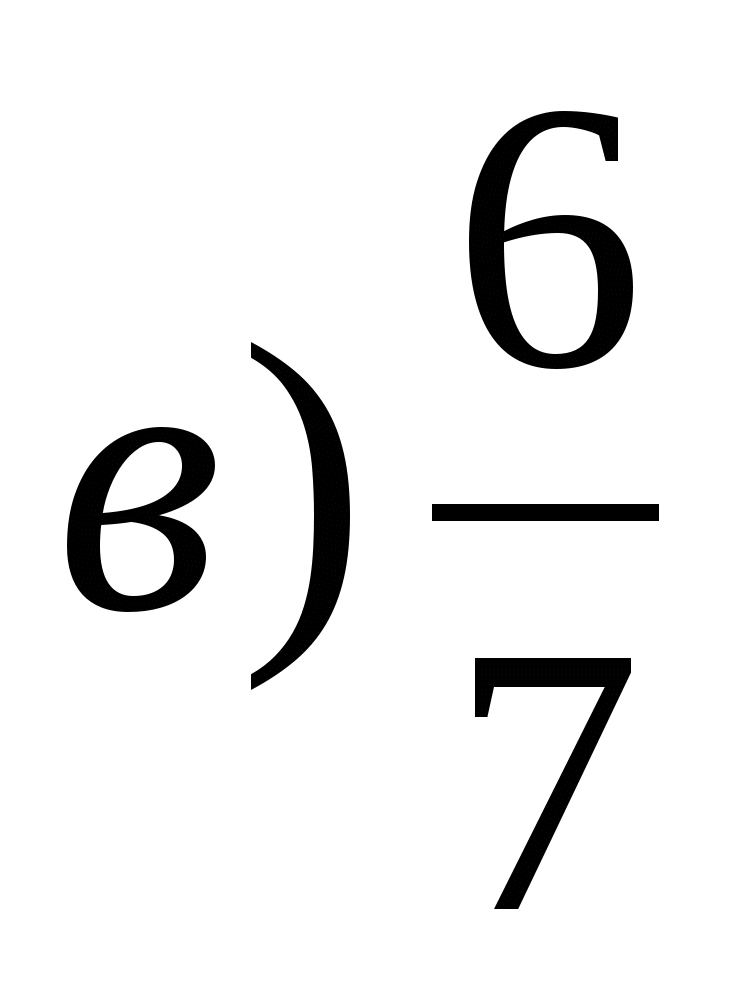 ‹
‹ 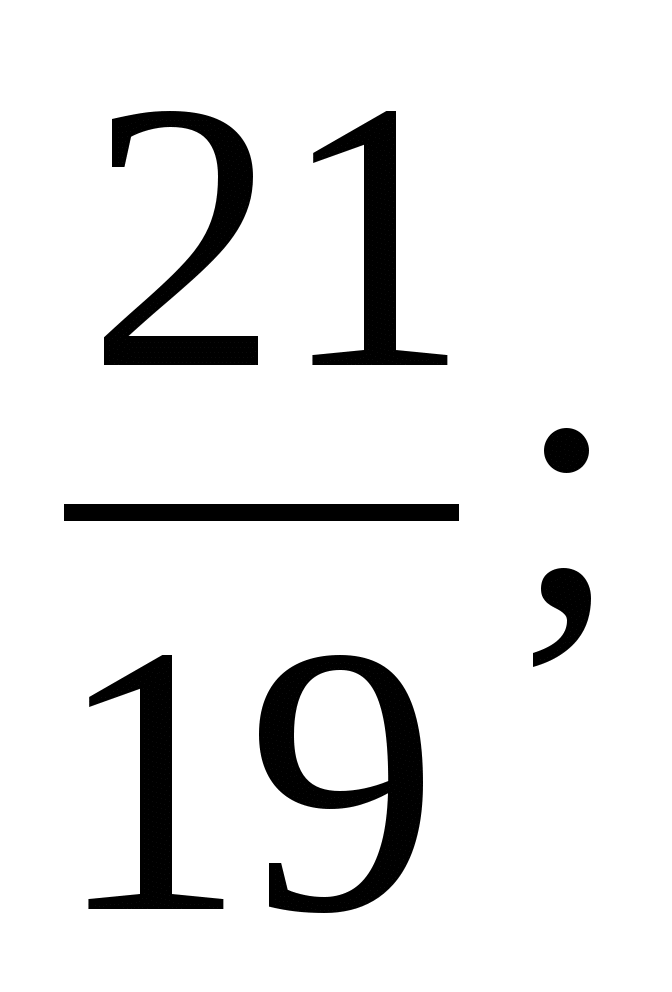 (порівняння з 1)
(порівняння з 1)
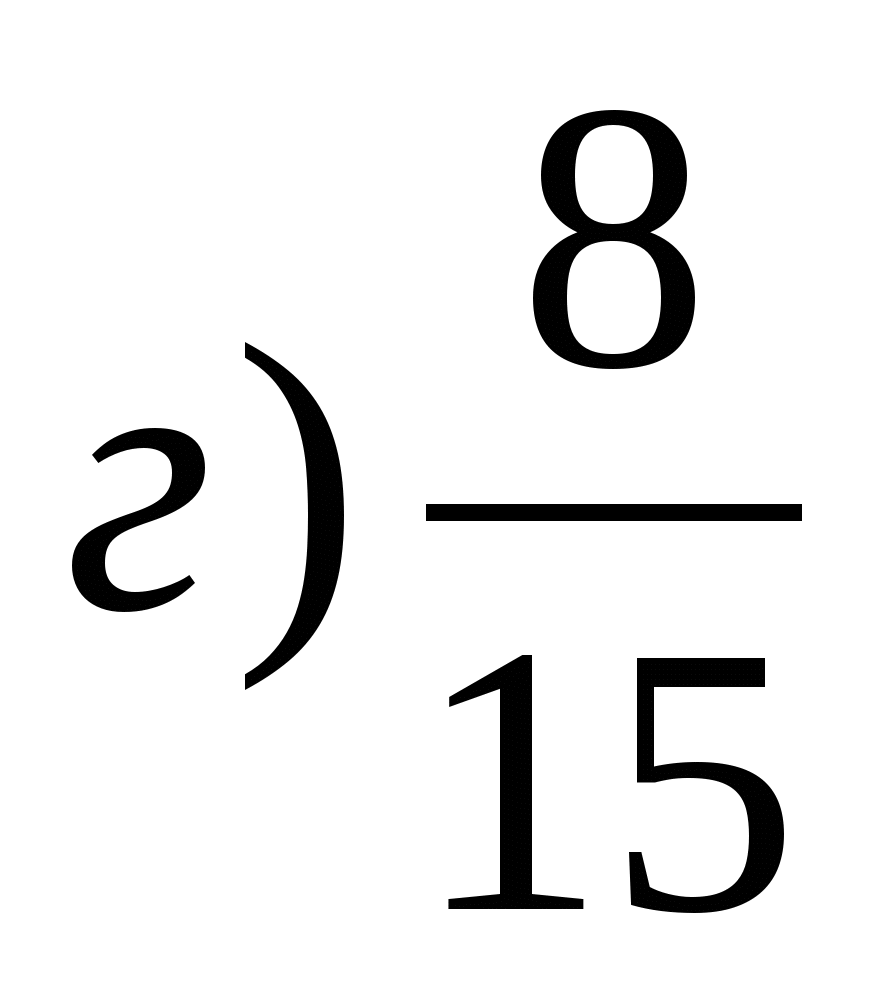 і
і 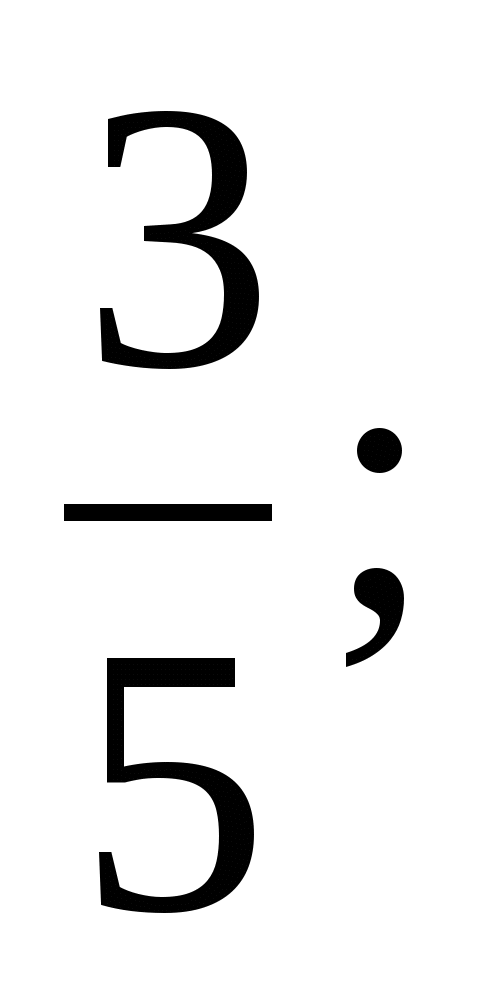
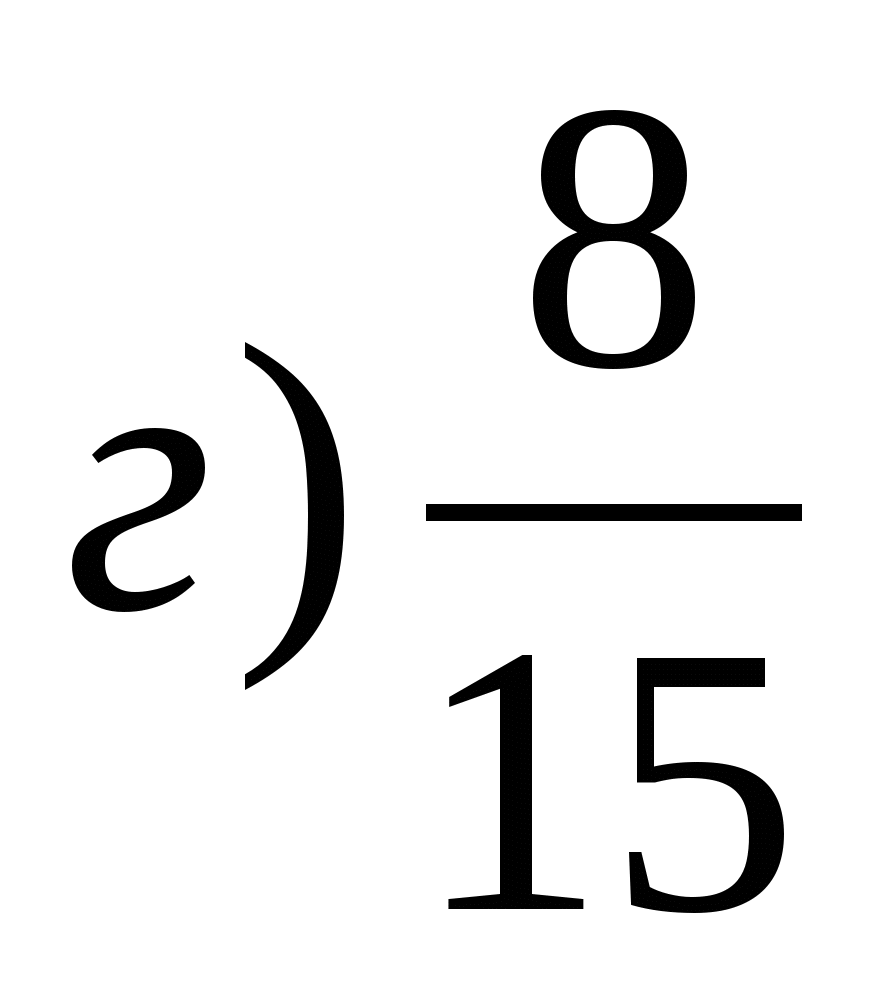 ‹
‹ 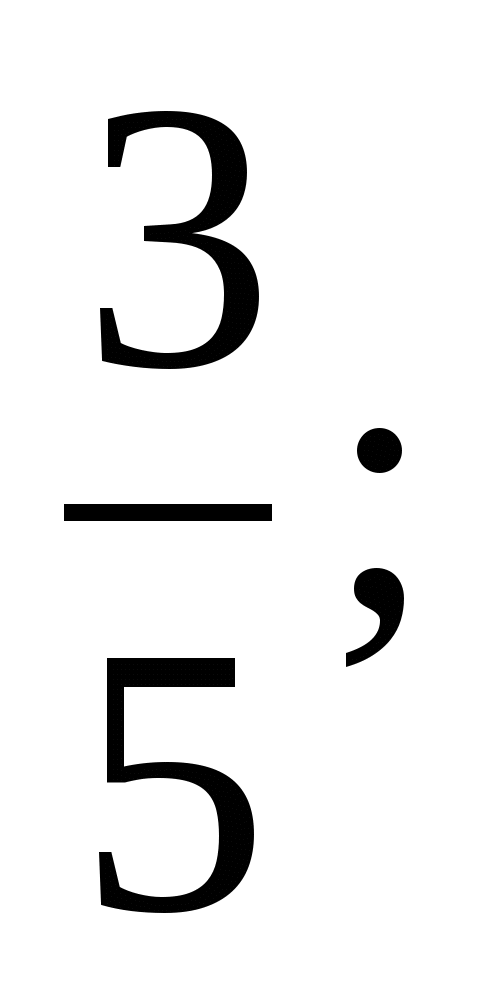 (Приведення до О.З.)
(Приведення до О.З.)
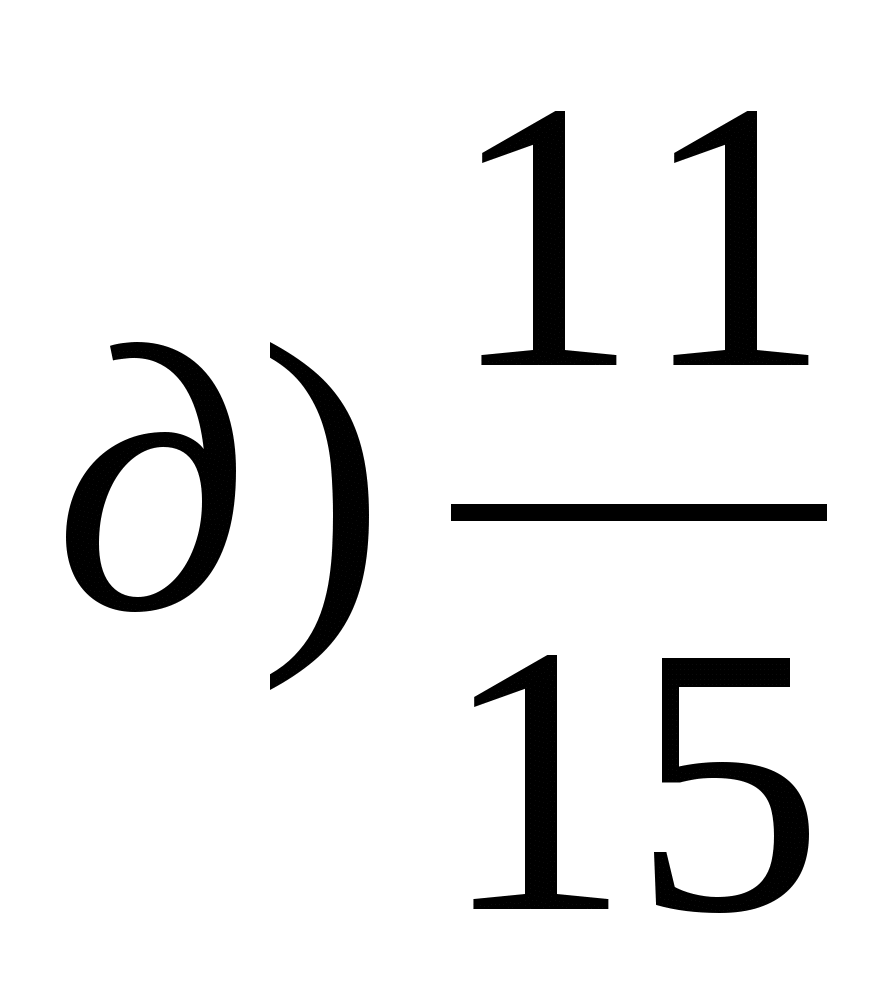 і
і 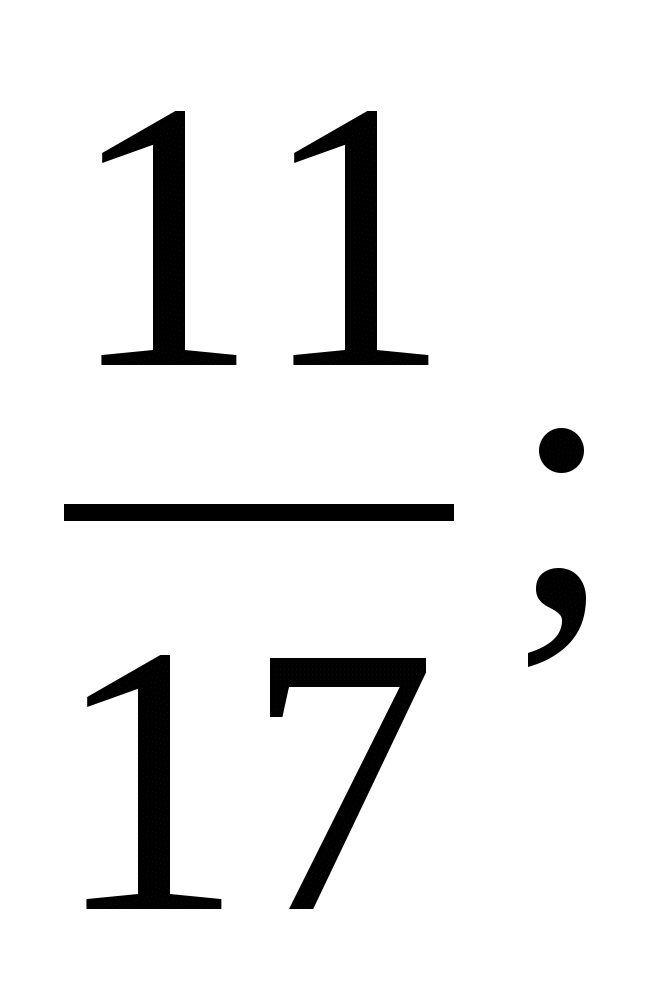
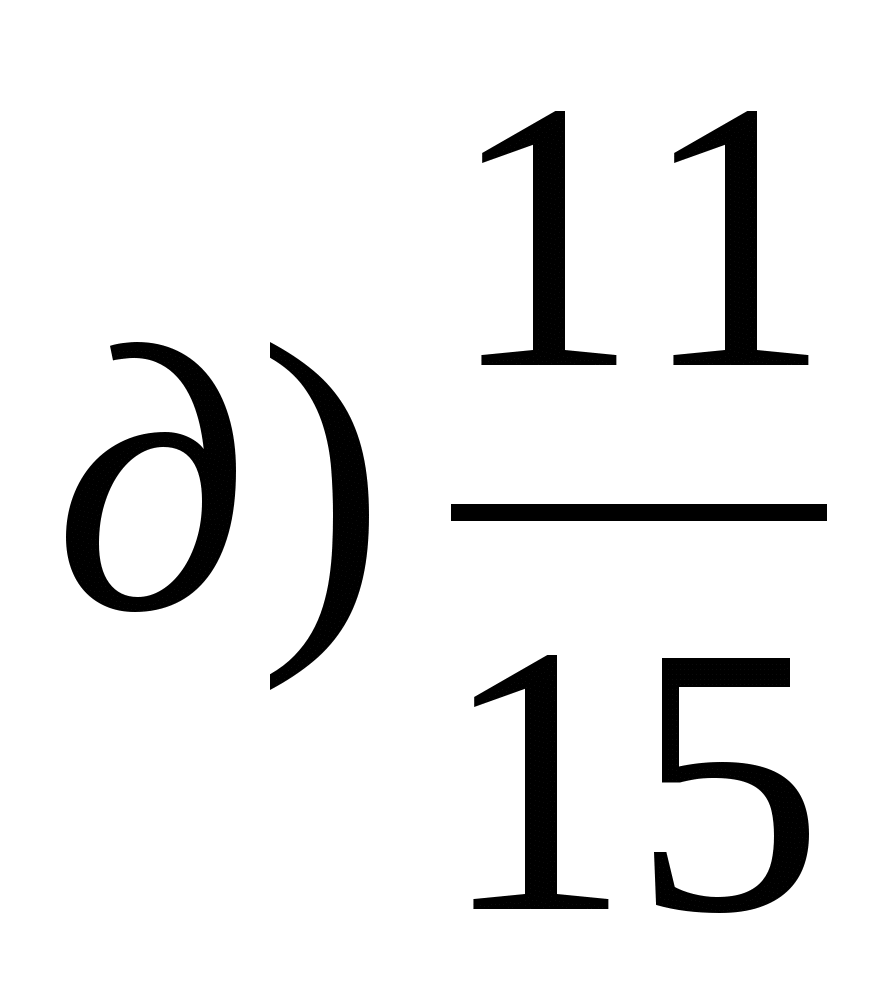 ›
› 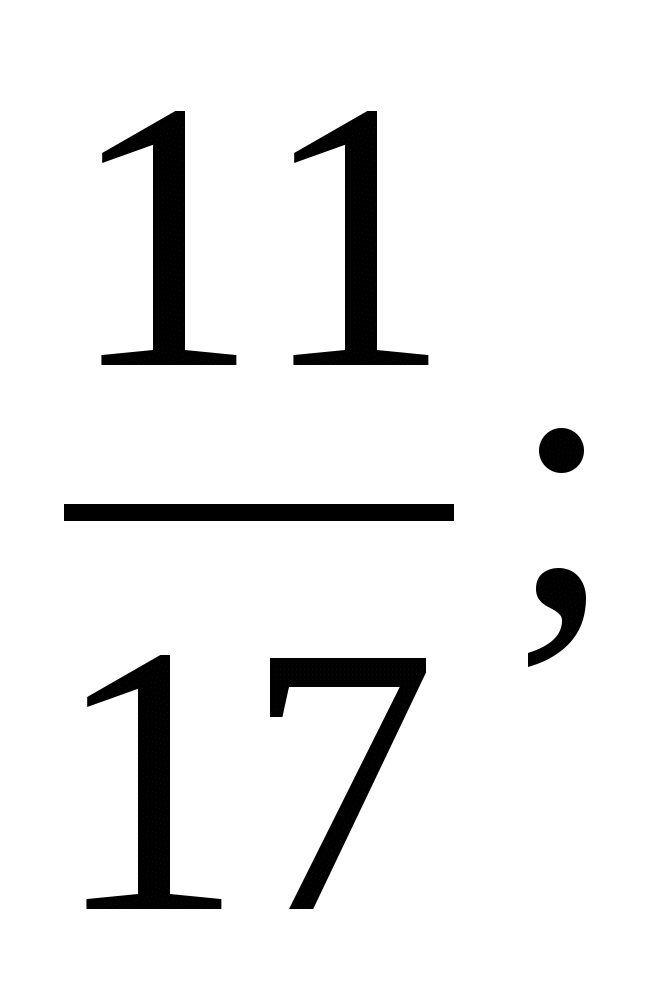 (за чисельником)
(за чисельником)
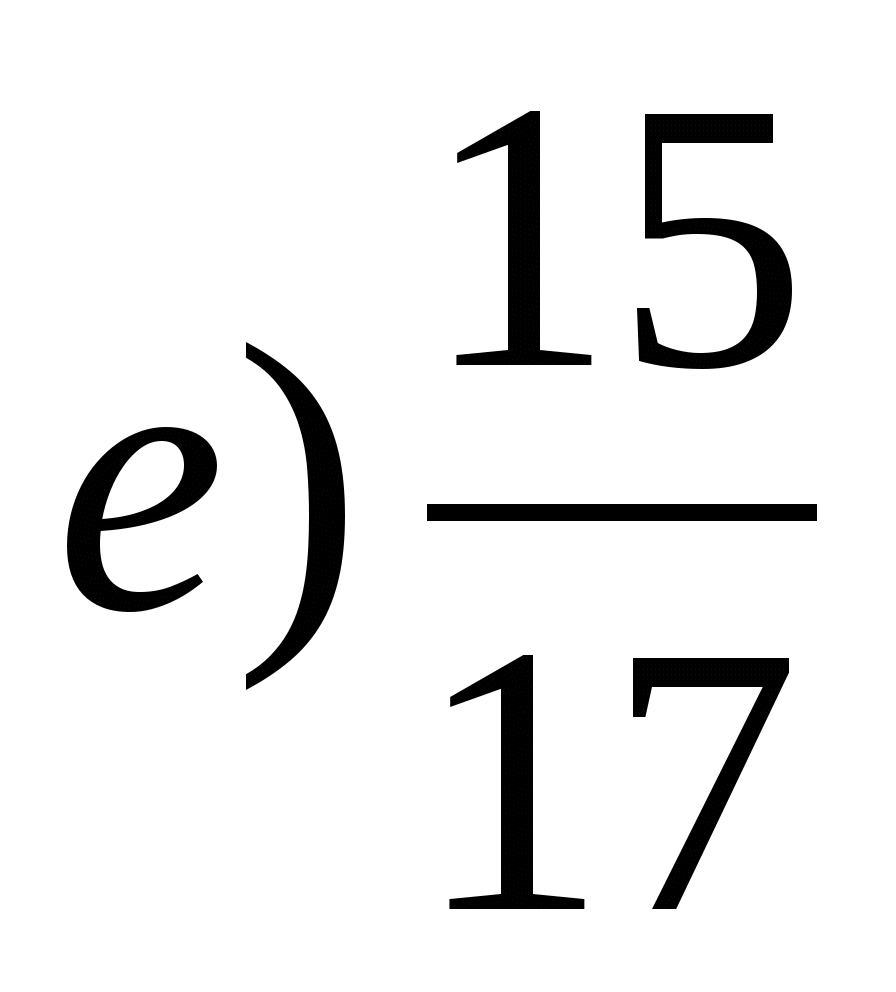 і
і 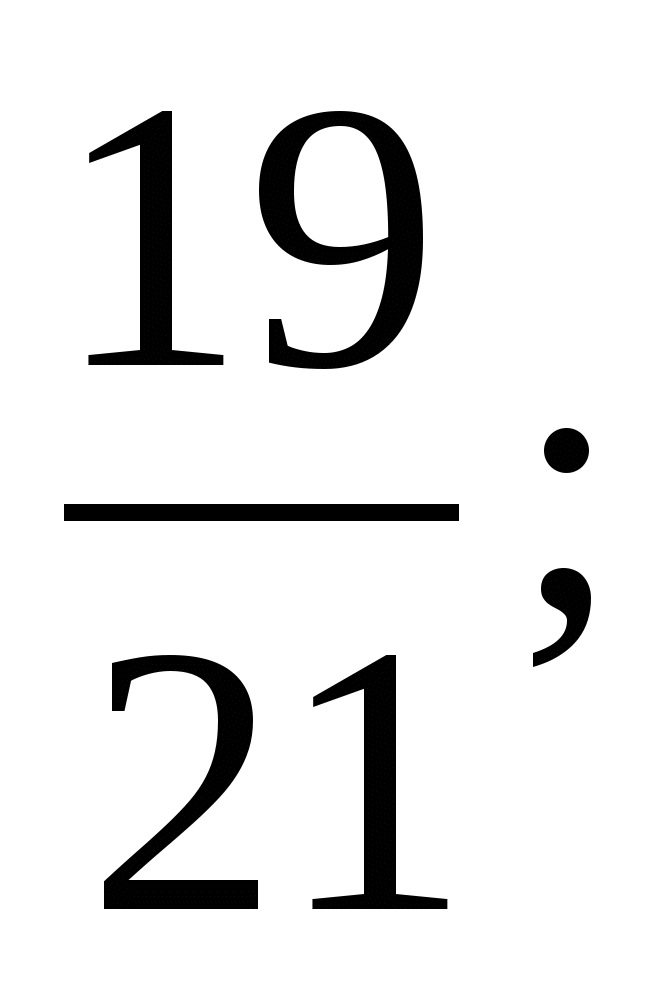
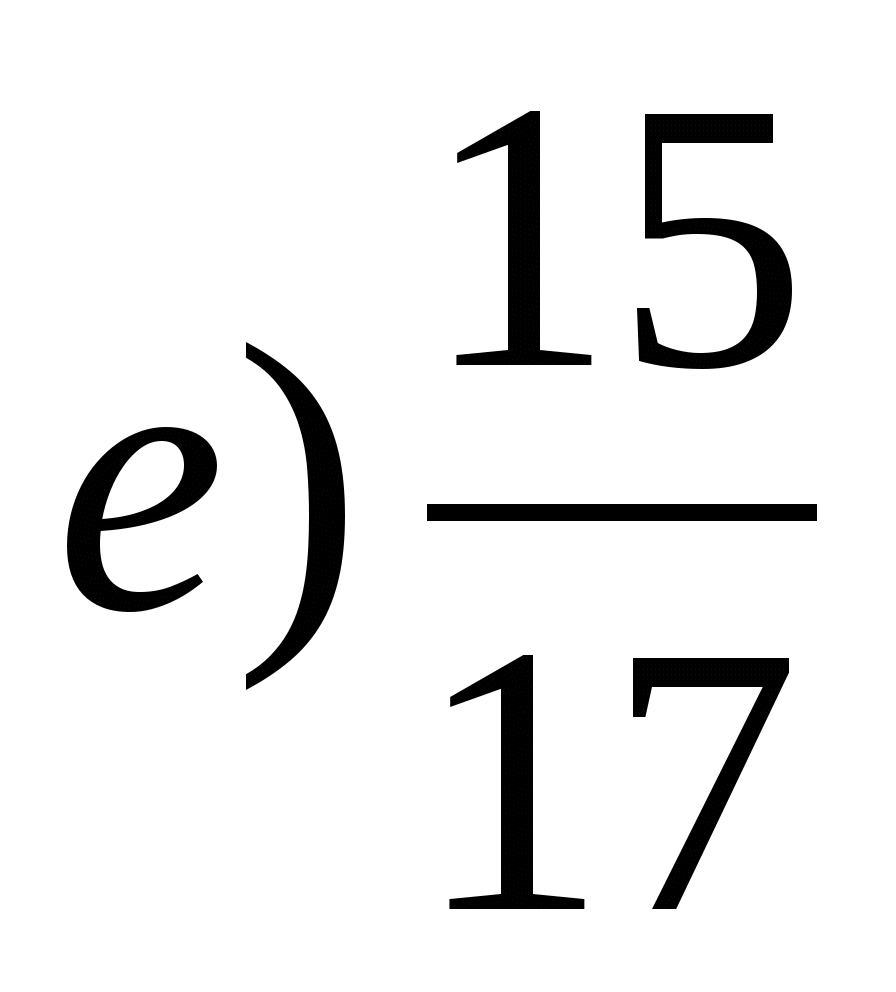 ‹
‹ 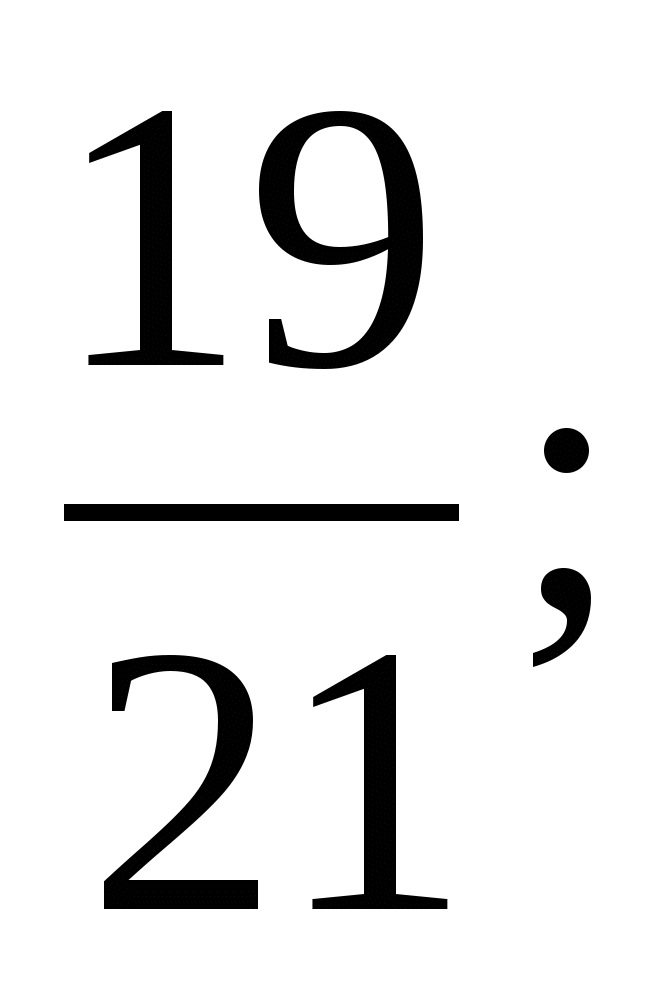 (за додатком до 1)
(за додатком до 1)
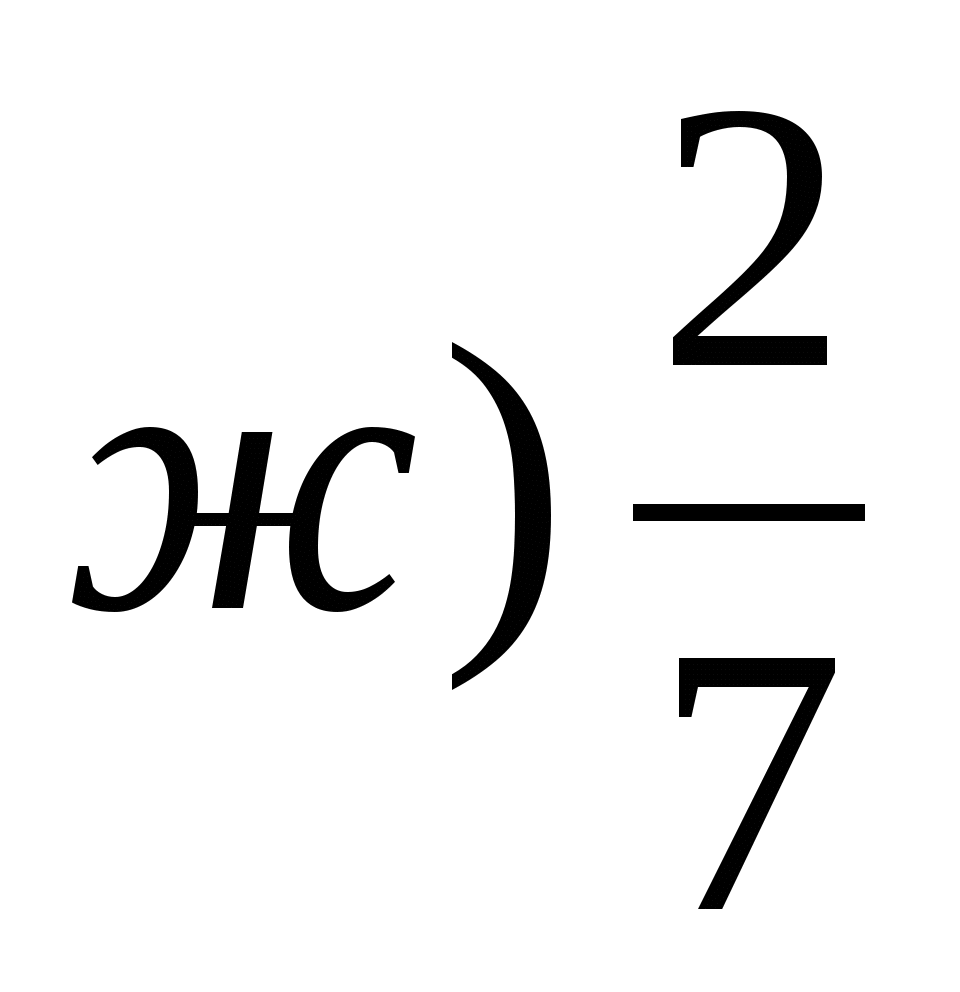 і
і 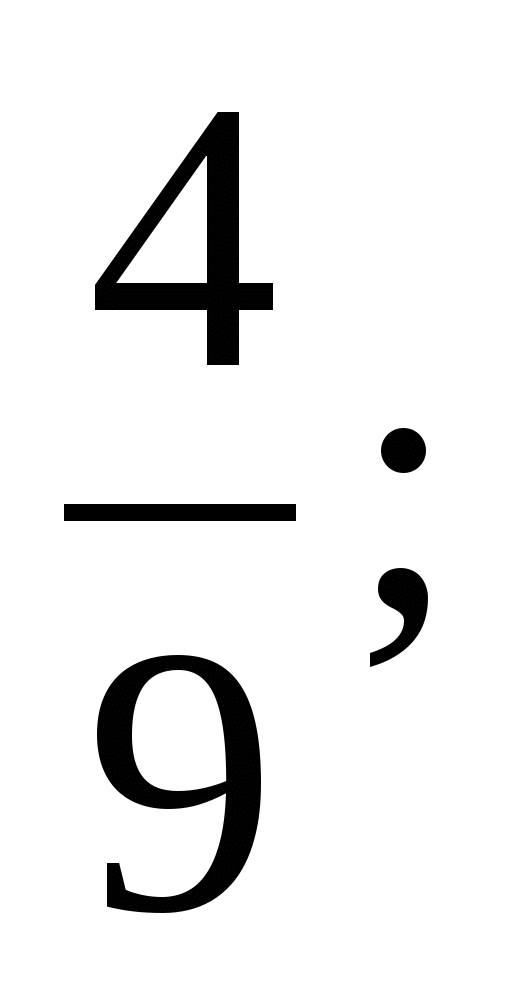
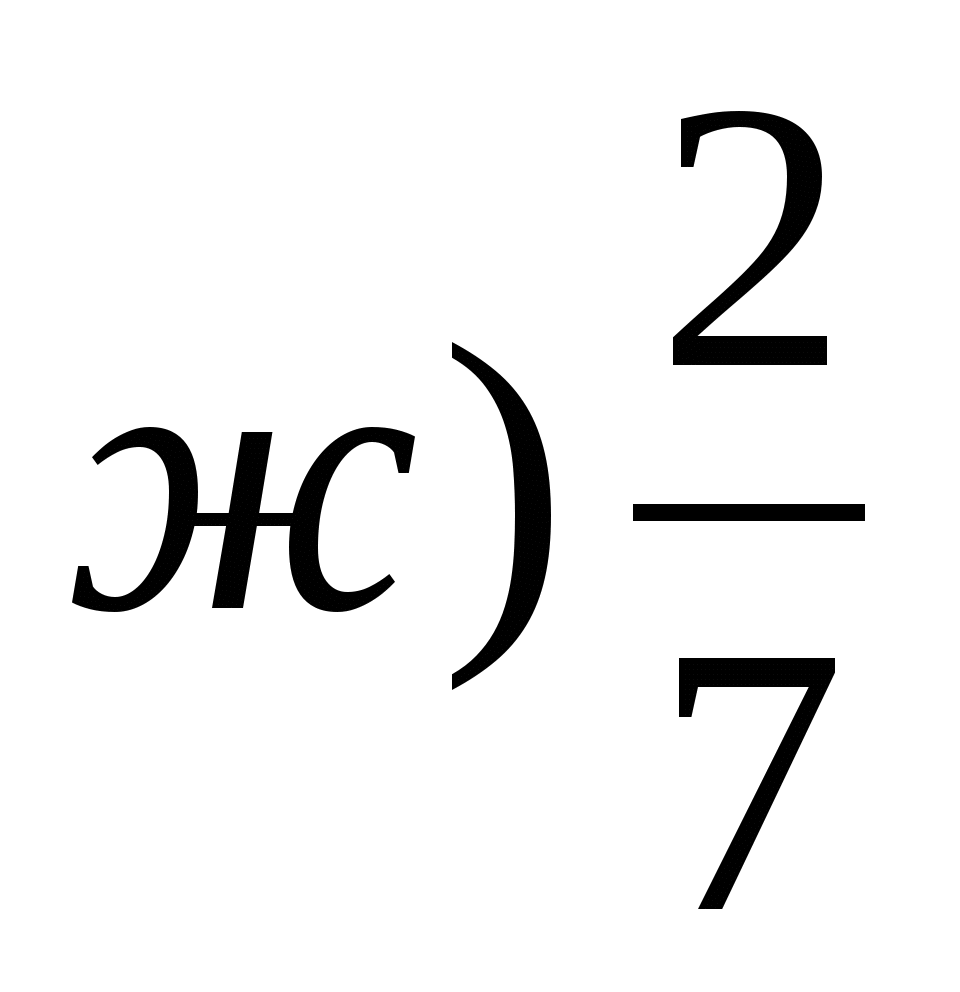 ‹
‹ 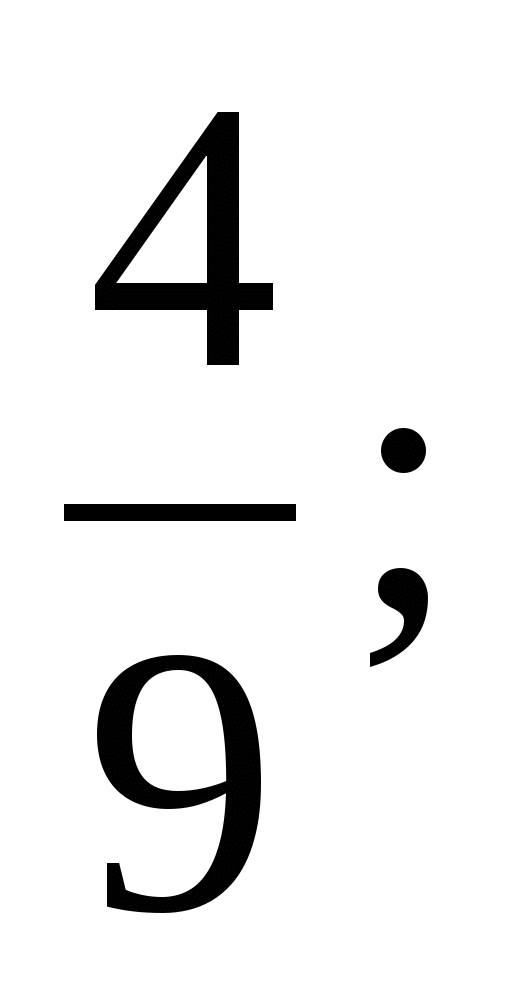 (Приведення до О.Ч.)
(Приведення до О.Ч.)
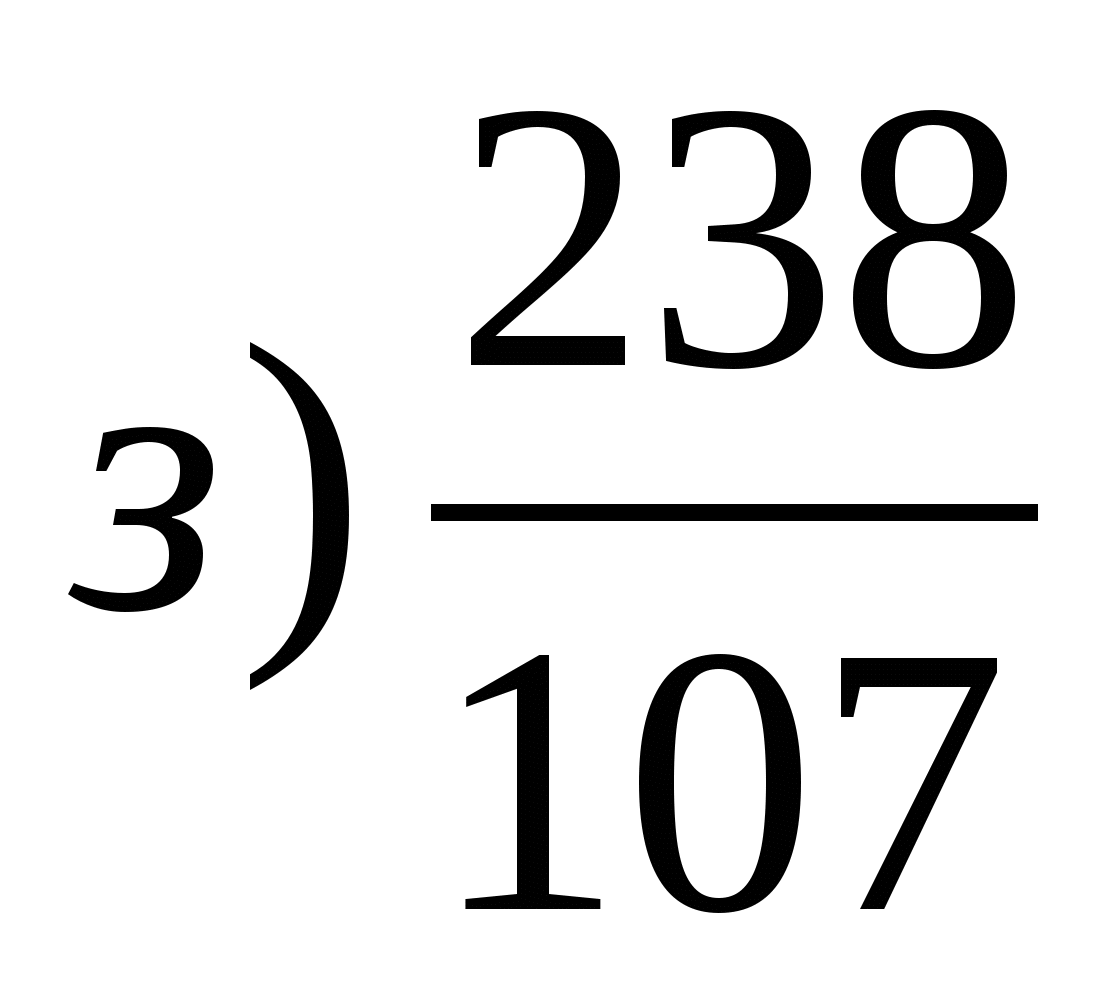 і
і 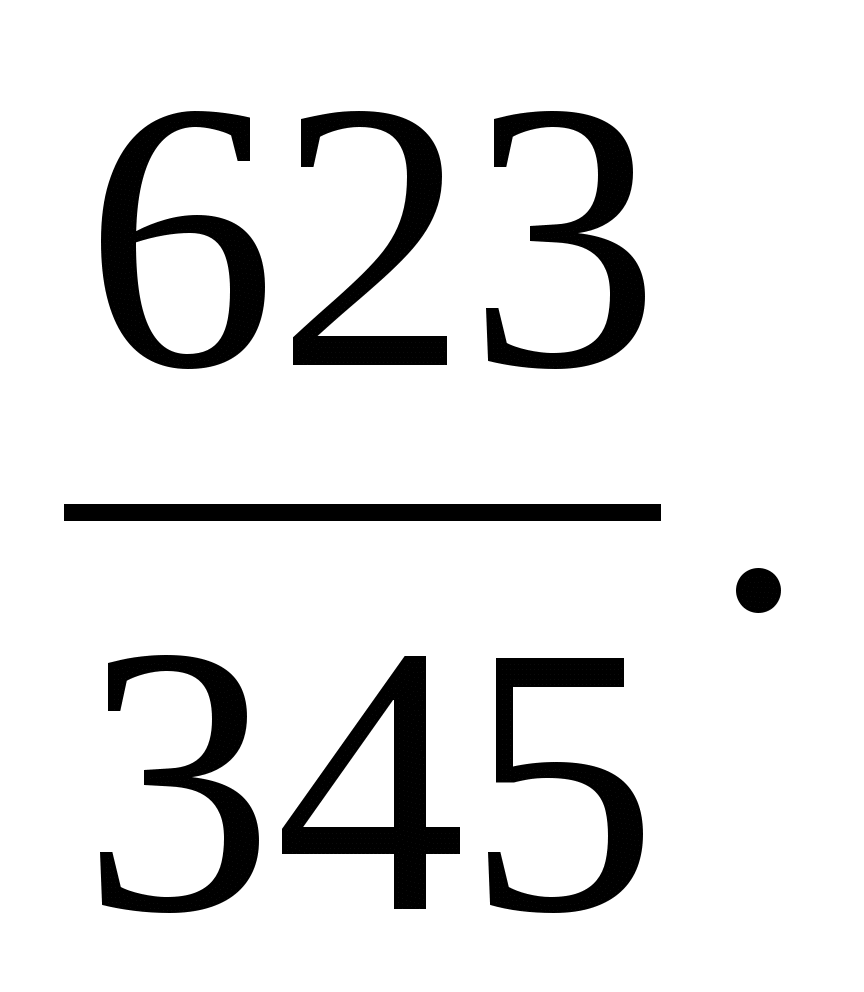
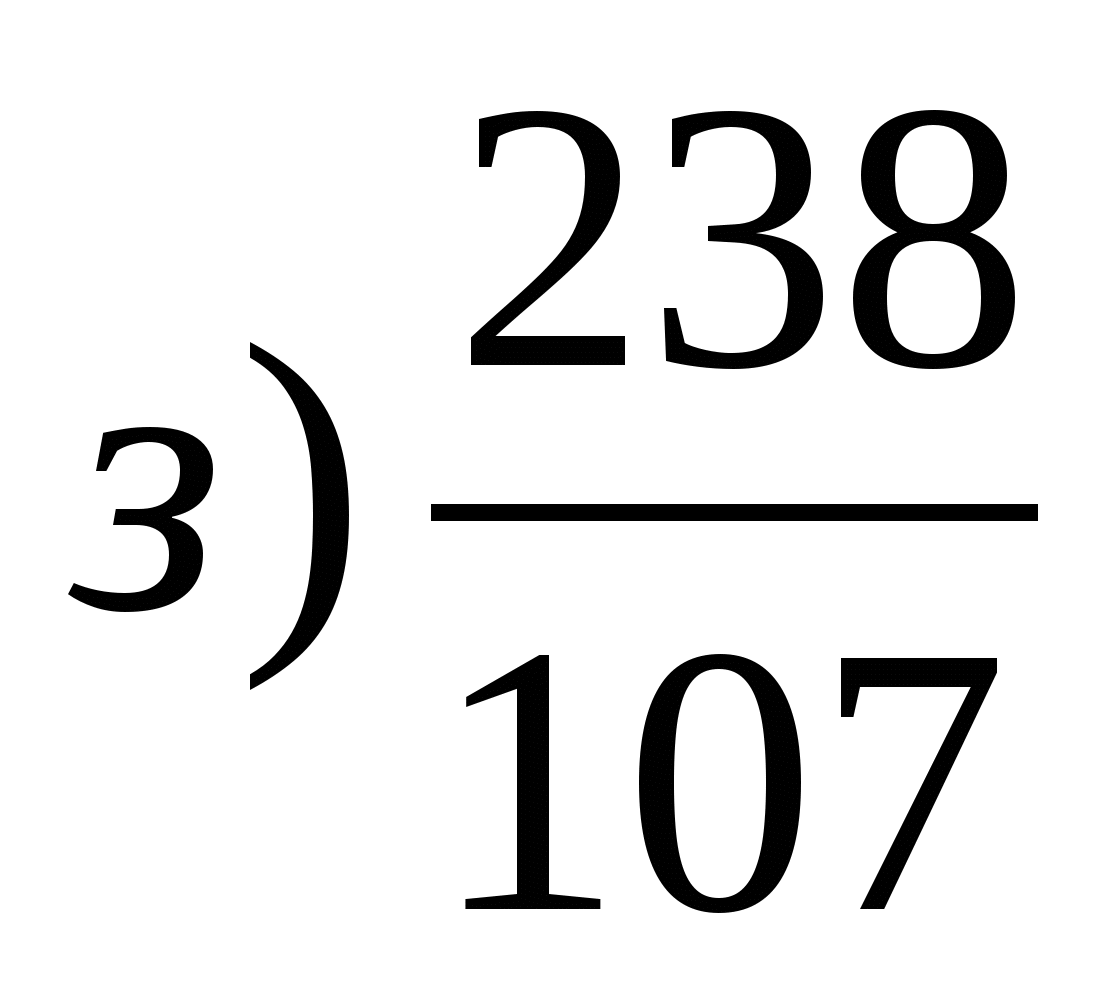 ›
› 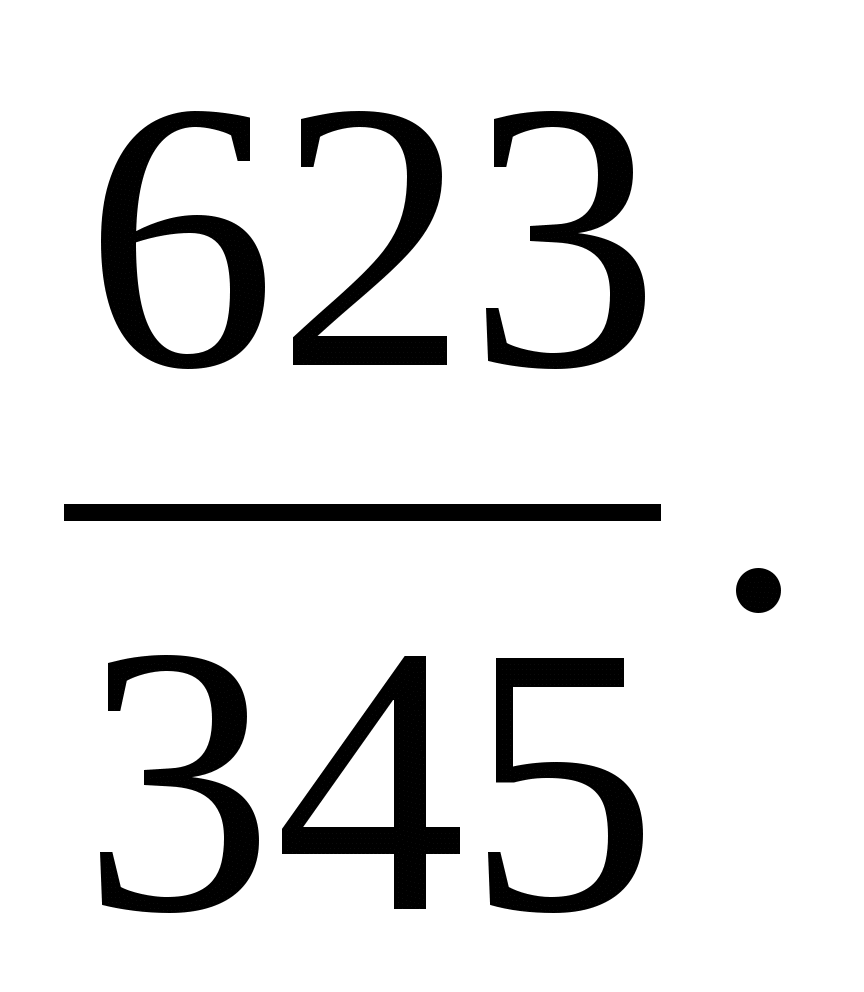 (СР з проміж.чис.)
(СР з проміж.чис.)
6. Самостійна робота із самоперевіркою у класі (5 хвилин).
Виконують завдання картки №2.
КАРТКА № 2
(самостійна робота з самоперевіркою)
Порівняйте дроби найбільш «зручним»
способом порівняння:
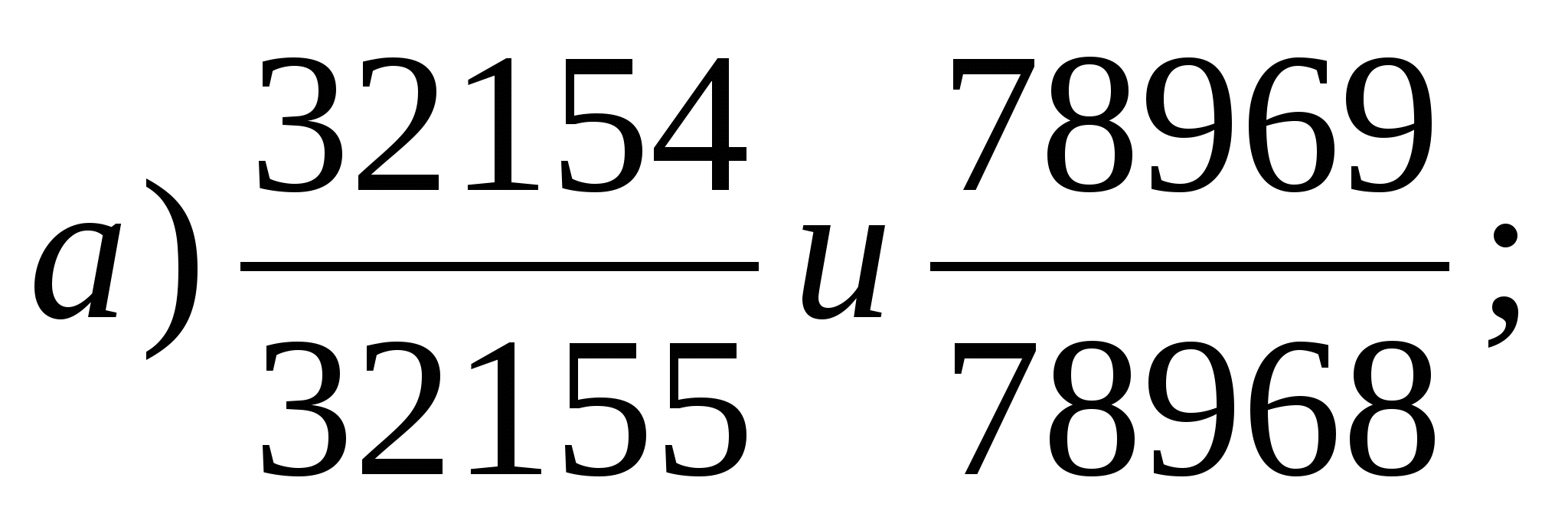
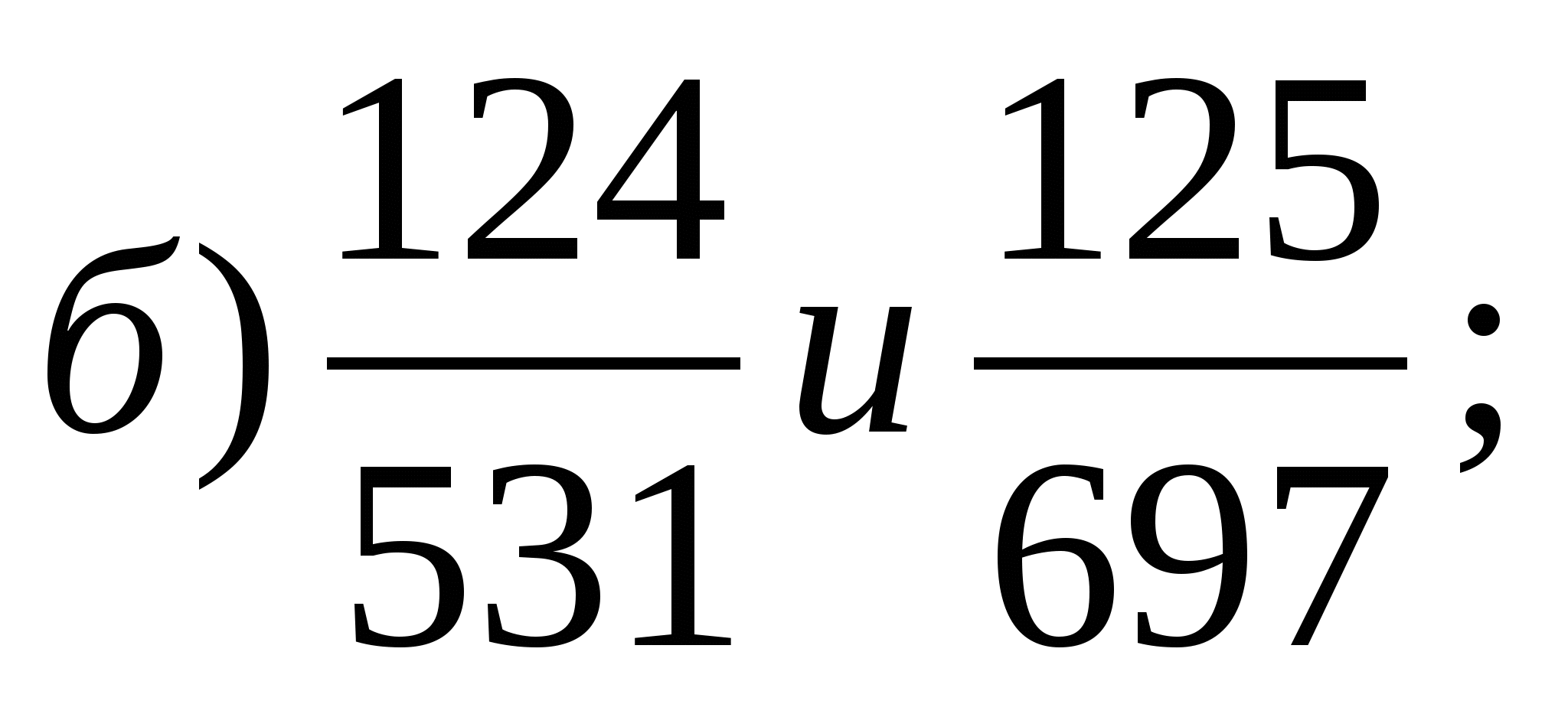
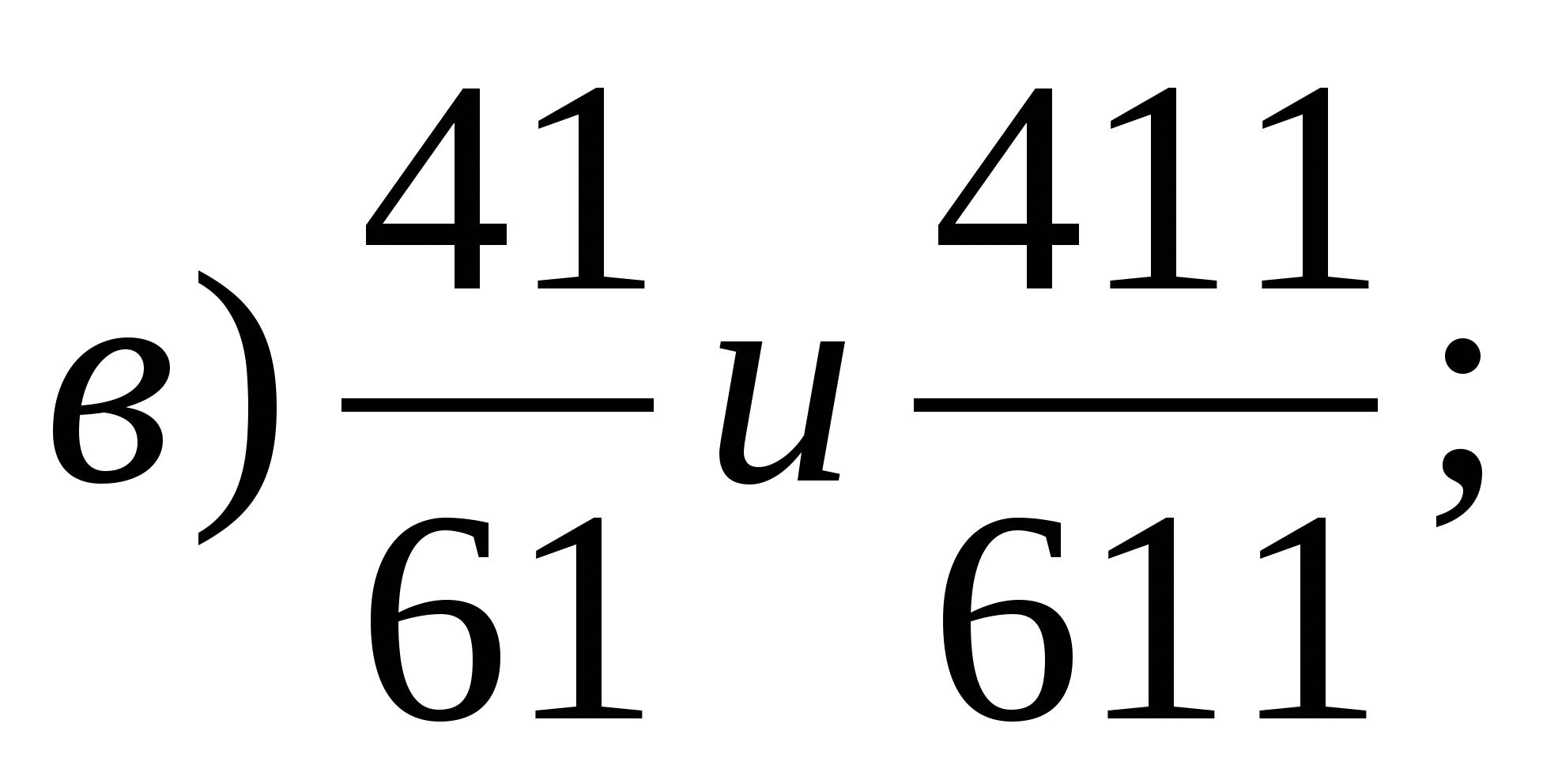
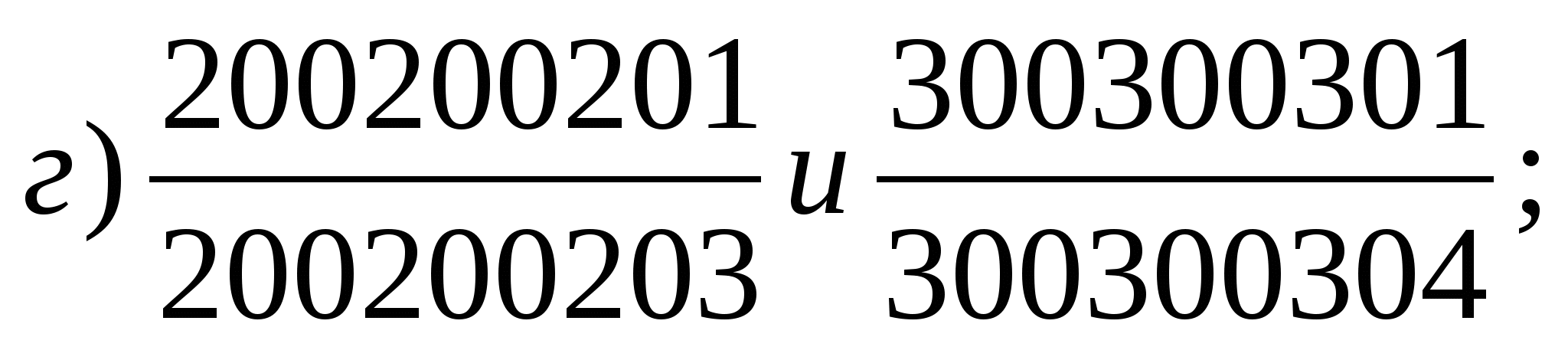

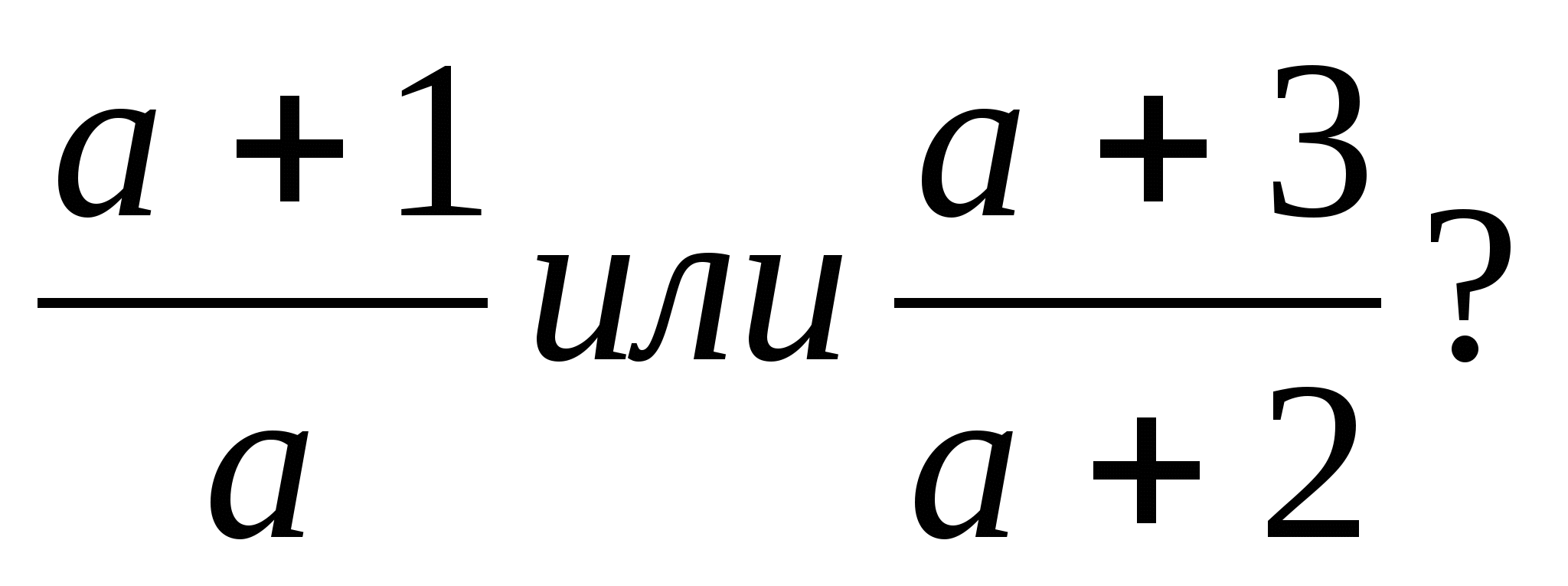
Відповіді самостійної роботи
Порівняйте дроби найбільш «зручним»
способом порівняння:
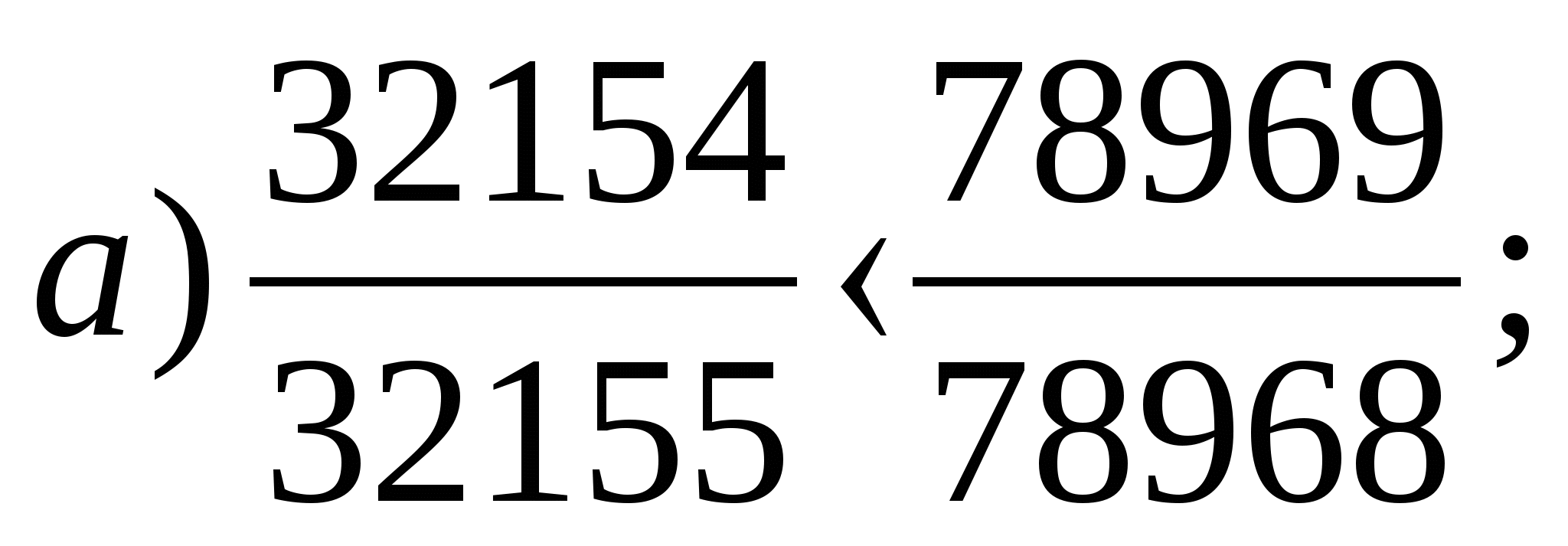
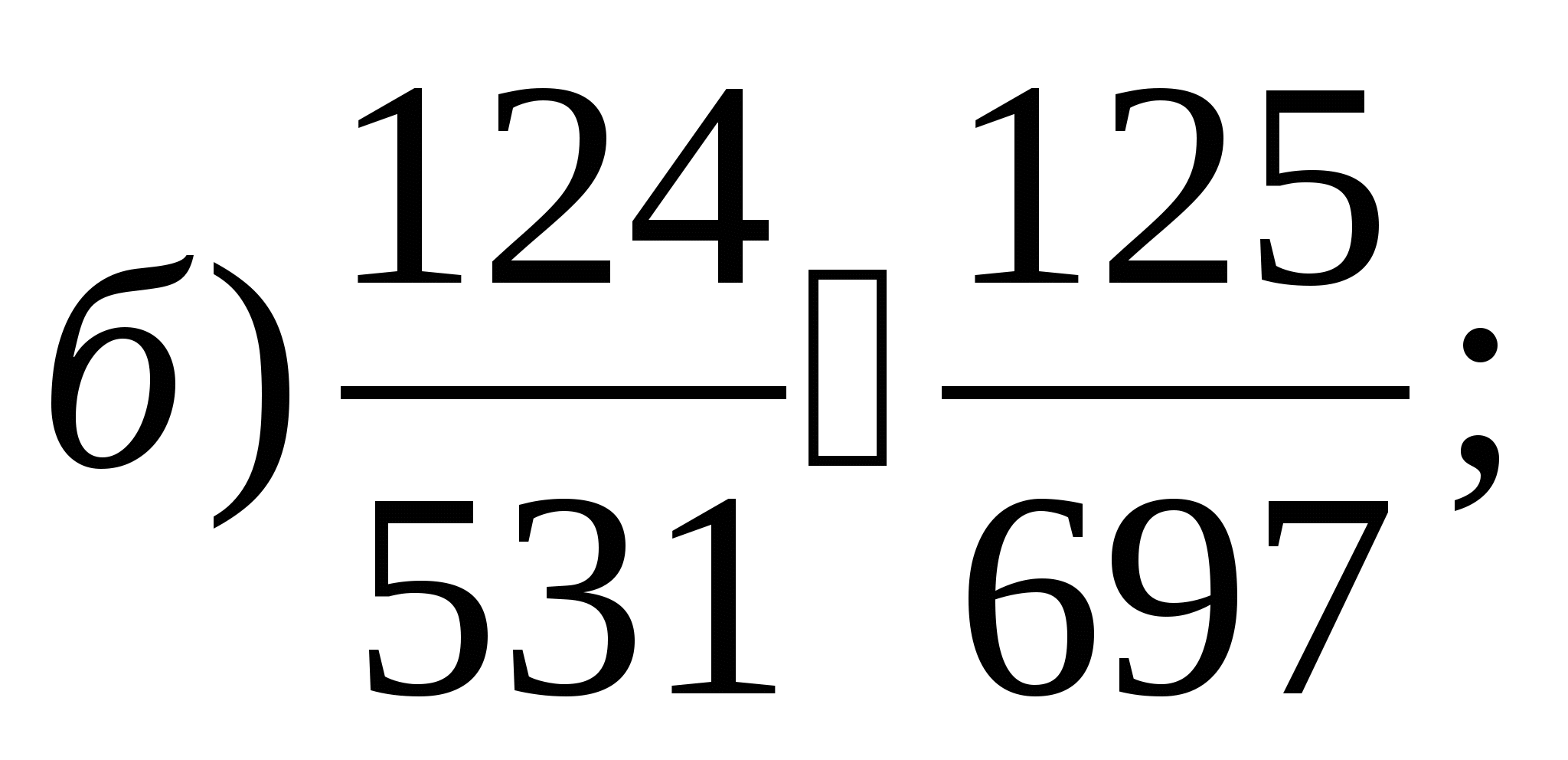
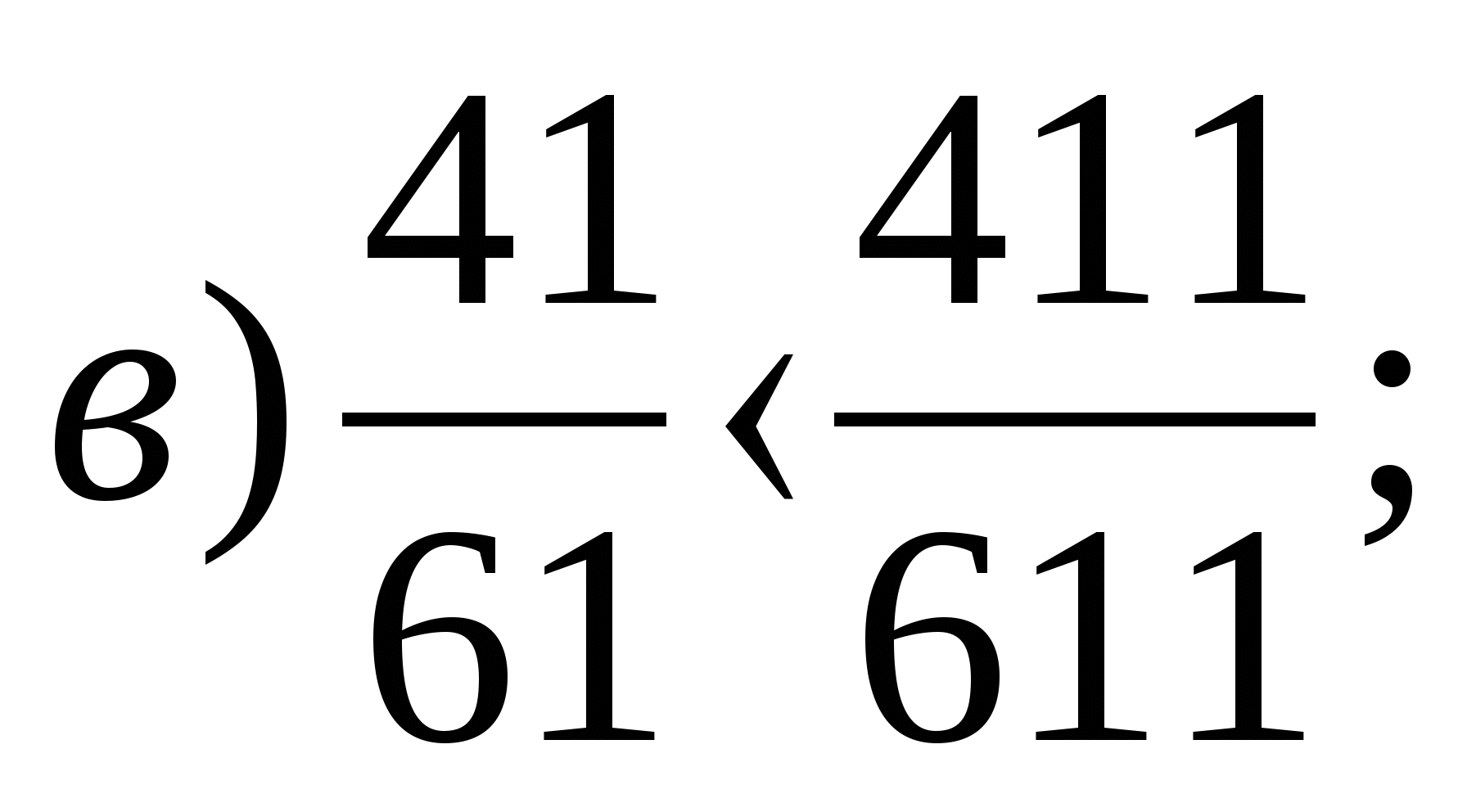
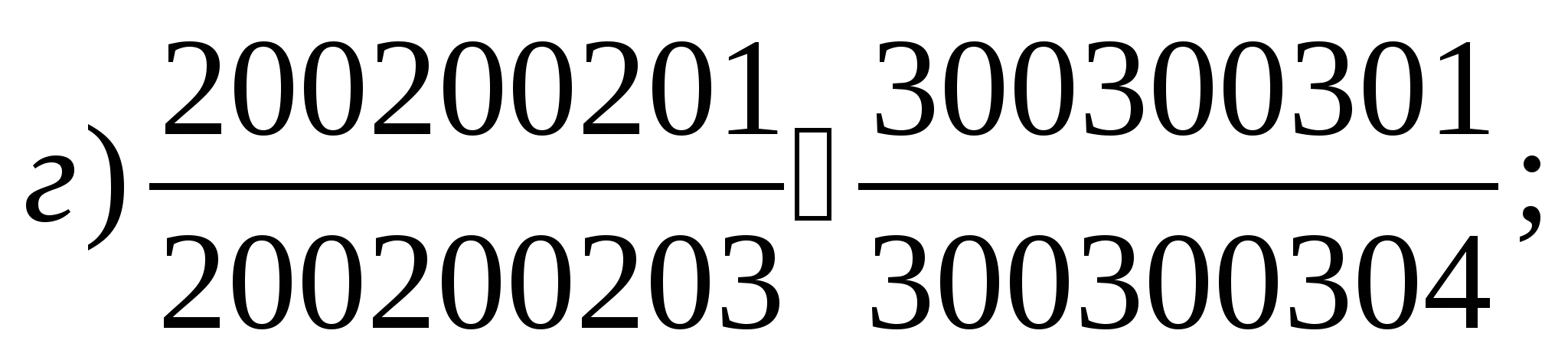
(Самопровірка за відповідями на закритій дошці).
Підніміть руки, у кого є помилки? Який алгоритм застосували неправильно?
На якому завданні зупинитися та розібратися?
(Вчитель працює індивідуально з тими, хто припустився помилок.)
Вони виконують №147 (1 – 6) підручника.
7. Включення до системи знань.
1. Скоротіть та порівняйте отримані дроби:
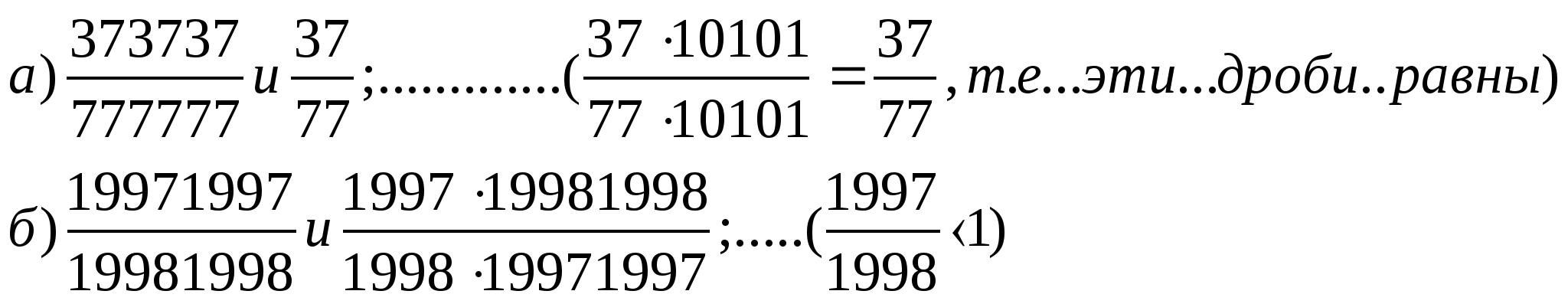
2. № 153 стор. 32 підручника
8. Дача домашнього завдання.
Г.3 §1 п.3 стор.30, № 145, 174 (3, 4, 5), 176, Д. № 185.
9. Рефлексія.
Чи виконали ми з Вами завдання на початку уроку?
Чи поповнився посуд наших знань про способи порівняння звичайних дробів?
Чи зовсім він повний?
Що це може означати?
Справді, нам ще залишилося заповнити шийку і там ми розмістимозагальне правило порівняння звичайних дробів, але це тема нашого наступного уроку.
А закінчити наш майстер клас я б хотіла словами Л.Толстого, який якось помітив, що людина подібна до дробу, чисельник якого є те, що людина є, а знаменник - те, що він думає про себе.
Як Ви вважаєте, яким дробом правильним чи неправильним краще бути?
А яким дробом Ви оцінили б свою діяльність на уроці, прийнявши за чисельник, обсяг отриманих знань у результаті нашої діяльності, а за знаменник обсяг запропонованих знань та способів їх досягнень?
І з яким настроєм Ви залишаєте цей урок? (Зафарбуй мордочку, що відповідає твого настрою).
Зафарбуйте той трикутник, який відповідає Вашому душевному стану зараз.

Додаток 1. (Картки 1 - 4)
Для роботи у парах.
До – 1

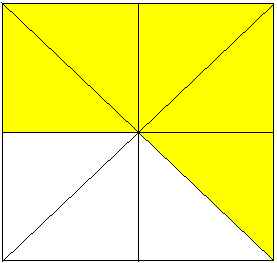
До - 2
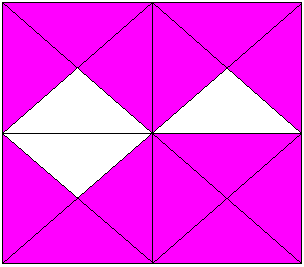

До - 3
До - 4
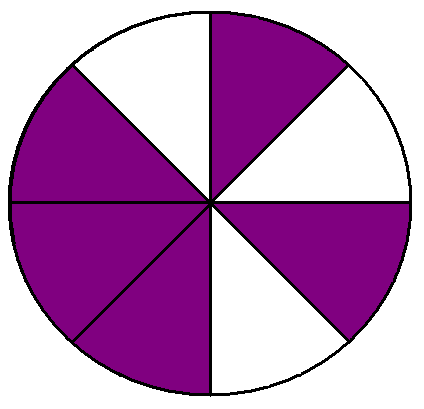

Схема аналізу уроку у технології діяльнісного методу навчання.
1.Включення дітей у діяльність.2. Виділення змістовної галузі
Чи спостерігається готовність до навчальної діяльності?
Актуалізація знань
1.Актуалізація ЗУН та розумових операцій, достатніх для побудови нового знання.
2.Фіксування складнощі в індивідуальній діяльності.
1.Чи відповідають завдання змістовної установки уроку.
2. Чи вільно володіють діти запропонованим змістом?
3. Чи виявляються причини помилок?
4. Чи є індивідуальною діяльність дітей у проблемній ситуації?
5. Чи зафіксовано самими дітьми заплановану скруту?
Постановка проблеми
Виявлення та фіксування у гучному мовленні:
1.де і чому виникло утруднення;
2.теми і цілі уроку.
1. Чи вказали діти самостійно причину утруднення?
2.Выявлено самими дітьми суттєву ознаку нового способу дії?
3.Не порушується вчителем роль організатора (а чи не учасника) комунікації?
4. Чи зафіксована дітьми тема і ціль уроку?
"Відкриття" дітьми нового знання
1.Вибір методу вирішення проблемної ситуації.
2.Підведення дітей до «відкриття» нового знання за допомогою діалогу, що підводить або спонукає.
3.Використання матеріальних чи матеріалізованих моделей.
4.Фіксування нового способу дії у мові та знаково.
1. Чи обраний метод вирішення проблемної ситуації дітьми самостійно?
2.Запропоновано вирішення проблеми самими дітьми?
3. Чи не порушується вчителем роль організатора (а чи не учасника) комунікації?
4. Використані матеріальні чи матеріалізовані моделі?
5. Чи достатньо чітко зафіксовано новий спосібдій?
Первинне закріплення
1.Решение дітьми типових завдань новий спосіб действий.
2. Промовляння способу вирішення у гучному мовленні.
1. Чи узгоджено процес вирішення завдання та його коментування?
2. Яка частина дітей включена до коментування рішення?
3. Чи успішно діти впоралися із запропонованими завданнями?
4. Грамотна чи математична мова?
Самостійно. робота з самоперевіркою у класі
1. Самостійне рішення та самоконтроль дітьми типових завдань на новий спосіб дії.
2.Створення мотивації на успіх для кожної дитини.
1. Чи самостійно діти перевірили свою роботу?
2.Какая частина дітей правильно її виконала?
3. Чи організовано коригування знань дітей, які не впоралися з роботою?
4. Чи створена мотивація на успіх для кожної дитини?
Повторення
1.Включення нового знання до системи знань.
2.Рішення завдань на повторення та закріплення вивченого раніше.
1.Какая частина дітей включено у самостійне вирішення завдань повторення?
2. Чи реалізовані в процесі виконання завдань заплановані цілі повторення?
Підсумок заняття
1.Рефлексія діяльності на уроці. (Що нового дізналися? Яким способом?)
2.Самоаналіз дітьми своєї діяльності.
3.Домашнє завдання (елемент вибору, квазітворчості, відсутність навантаження).
1. Чи правильно зафіксували діти отримане на уроці нове знання?
2. Чи проведена самооцінка дітьми своєї діяльності? Який результат?
3. Який емоційний та психологічний стан дітей?
Яке із чисел більше: чи? Відповідь очевидна. А тепер: чи? Вже не так очевидно, правда? А так: чи?
Часто потрібно знати, яке з числових виразівбільше. Наприклад, щоб при розв'язанні нерівності розставити крапки на осі у правильному порядку.
Зараз навчу тебе порівнювати такі цифри.
Якщо треба порівняти числа і, між ними ставимо знак (походить від латинського слова Versus або скорочено vs. - Проти): . Цей знак замінює невідомий нам знак нерівності ( ). Далі будемо виконувати тотожні перетворення доти, доки стане ясно, який саме знак потрібно поставити між числами.
Суть порівняння чисел полягає в наступному: ми ставимося до знака так, ніби це якийсь знак нерівності. І з виразом ми можемо робити все те, що робимо зазвичай з нерівностями:
- додати будь-яке число до обох частин (і відняти, звичайно, теж можемо)
- «перенести все в один бік», тобто відняти з обох частин одне з порівнюваних виразів. На місці віднімається вирази залишиться: .
- домножувати чи ділити одне й те саме число. Якщо це число негативне, символ нерівності змінюється протилежний: .
- зводити обидві частини на ту саму ступінь. Якщо цей ступінь - парний, необхідно переконатися, що обидві частини мають однаковий знак; якщо обидві частини позитивні, при зведенні на ступінь знак не змінюється, а якщо негативні, тоді змінюється на протилежний.
- витягти корінь однакового ступеняз обох частин. Якщо вилучаємо корінь парного ступеня, необхідно заздалегідь переконатися, що обидва вирази невід'ємні.
- будь-які інші рівносильні перетворення.
Важливо: перетворення бажано робити такими, щоб знак нерівності не змінювався! Тобто в ході перетворень небажано примножувати на негативне число, і не можна зводити до квадрата, якщо одна з частин негативна.
Розберемо кілька типових ситуацій.
1. Зведення на ступінь.
приклад.
Що більше: чи?
Рішення.
Оскільки обидві частини нерівності позитивні, можемо звести в квадрат, щоб позбавитися кореня:
приклад.
Що більше: чи?
Рішення.
Тут теж можемо звести в квадрат, але це нам допоможе позбутися лише від квадратного кореня. Тут треба зводити в такий ступінь, щоб обидва корені зникли. Отже, показник цього ступеня повинен ділитися і (ступінь першого кореня), і. Таким числом є, отже, зводимо в -ю ступінь:
2. Множення на сполучене.
Сполученимназивається множник, що доповнює вираз до формули різниці квадратів: - сполучене для і навпаки, т.к. .
приклад.
Що більше: чи?
Рішення.
Домножимо і розділимо кожну різницю на сполучену суму:
Очевидно, що знаменник у правій частині більший за знаменник у лівій. Тому правий дріб менше лівого:
3. Віднімання
Згадаймо, що.
приклад.
Що більше: чи?
Рішення.
Звичайно, ми могли б звести все в квадрат, перегрупувати і знову звести в квадрат. Але можна вчинити хитріше:
приклад.
Порівняйте числа і.
Рішення.
Згадуємо формули тригонометрії:
Перевіримо, у яких чвертях на тригонометричному колі лежать точки і.
4. Розподіл.
Тут також використовуємо просте правило: .
При або, тобто.
При знак змінюється: .
приклад.
Виконай порівняння: .
Рішення.
5. Порівняйте числа з третім числом
Якщо і то (закон транзитивності).
приклад.
Порівняйте.
Рішення.
Порівняємо числа не один з одним, а з числом.
Очевидно, що.
З іншого боку, .
приклад.
Що більше: чи?
Рішення.
Обидва числа більші, але менші. Підберемо таке число, щоб воно було більше одного, але менше іншого. Наприклад, . Перевіримо:
6. Що робити з логарифмами?
Нічого особливого. Як позбавлятися логарифмів, докладно описано в темі . Основні правила такі:
\[(\log _a)x \vee b(\rm( )) \Leftrightarrow (\rm( ))\left[ (\begin(array)(*(20)(l))(x \vee (a^ b)\;(\rm(при))\;a > 1)\\(x \wedge (a^b)\;(\rm(при))\;0< a < 1}\end{array}} \right.\] или \[{\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a >1)\(x \wedge y\;(\rm(при))\;0< a < 1}\end{array}} \right.\]
Також можемо додати правило про логарифми з різними підставами та однаковим аргументом:
Пояснити його можна так: чим більша підстава, тим менший рівень її доведеться звести, щоб отримати один і той же. Якщо ж підстава менша, то все навпаки, тому що відповідна функція монотонно спадає.
приклад.
Порівняйте числа: і.
Рішення.
Відповідно до вищеописаних правил:
А тепер формула для сучасних.
Правило порівняння логарифмів можна записати і коротше:
приклад.
Що більше: чи?
Рішення.
приклад.
Порівняйте, яке чисел більше: .
Існують певні правила порівняння чисел. Розглянемо наступний приклад.
Вчора термометр показував 15˚ C, а сьогодні показує 20˚ C. Сьогодні тепліше, ніж учора. Число 15 менше від числа 20, можемо записати так: 15< 20. А, если мы представим эти числа на координатной прямой, то точка со значением 15 будет расположена ліворуч від точкиіз значенням 20.
Нині ж розглянемо негативні температури. Вчора на вулиці було -12˚ C, а сьогодні -8˚ C. Сьогодні тепліше, ніж учора. Тому вважають, що число -12 менше від числа -8. На горизонтальній координатній прямій точка зі значенням -12 розташована лівіше від точки зі значенням -8. Можемо записати так: -12< -8.
Отже, якщо порівнювати числа за допомогою горизонтальної координатної прямої, із двох чисел меншим вважається те, зображення якого на координатній прямій розташоване лівіше, а більшим те, зображення якого розташоване правіше. Наприклад, у нас на малюнку А > B та C, але B > C.
На координатній прямій позитивні числа розташовуються праворуч від нуля, а негативні – ліворуч від нуля. додатне числобільше нуля, а всяке негативне менше нуля, і тому будь-яке негативне число менше будь-якого позитивного числа.
Отже, перше на що необхідно звернути увагу при порівнянні чисел, це знаки порівнюваних чисел. Число з мінусом (негативне) завжди менше позитивного.
Якщо ж ми порівнюємо два негативних числа, то потрібно порівняти їх модулі: більшим буде число, модуль якого менше, а меншим то число, модуль якого менше. Наприклад, -7 та -5. Числа, що порівнюються - негативні. Порівнюємо їх модулі 5 і 7. 7 більше ніж 5, отже -7 менше ніж -5. Якщо відзначити на координатній прямий два негативні числа, то лівіше виявиться менше, а більше буде розташовано правіше. -7 розташовано ліворуч -5, значить -7< -5.
 Порівняння звичайних дробів
Порівняння звичайних дробів
З двох дробів з однаковими знаменникамименше та, у якої менше чисельник, і більше та, у якої більший чисельник.
Можна порівнювати дроби лише з однаковими знаменниками.
Алгоритм порівняння звичайних дробів
1) Якщо у дробу є ціла частина, порівняння починаємо саме з нього. Більшим буде той дріб, у якого ціла частина більша. Якщо цілої частини дробів немає або вони рівні, переходимо до наступного пункту.
2) Якщо дроби з різними знаменникаминеобхідно привести їх до спільного знаменника.
3) Порівнюємо чисельники дробів. Більшим буде той дріб, у якого чисельник більший.
Зверніть увагу, дріб з цілою частиноюзавжди буде більше дробу без цілої частини.
Порівняння десяткових дробів
Десяткові дроби можна порівнювати лише з однаковою кількістю цифр (знаків) праворуч від коми.
Алгоритм порівняння десяткових дробів
1) Звертаємо увагу на кількість знаків праворуч від коми. Якщо кількість цифр однакова, можемо приступати до порівняння. Якщо – ні, дописуємо потрібну кількість нулів в одному з десяткових дробів.
2) Порівнюємо десяткові дроби зліва направо: цілі з цілими, десяті з десятими, соті з сотими тощо.
3) Більшим буде той дріб, у якому одна з частин виявиться більшою, ніж у іншому дробі (порівняння починаємо з цілих чисел: якщо ціла частина одного дробу більша, значить, і весь дріб більший).
Наприклад, порівняємо десяткові дроби:
1) Допишемо в першому дробі необхідну кількість нулів, щоб зрівняти кількість знаків після коми
57,300 та 57,321
2) Порівнювати починаємо зліва направо:
цілі з цілими: 57 = 57;
десяті з десятими: 3 = 3;
соті з сотими: 0< 2.
Бо соті першою десяткового дробувиявилися меншими, весь дріб і буде меншим:
57,300 < 57,321
www.сайт, при повному або частковому копіюванні матеріалу посилання на першоджерело обов'язкове.


