Дії з дробовими показниками та корінням приклади. Визначення ступеня з дробовим показником

1)Ступені з натуральним показником:

У країні чисел виникли проблеми. Астрономи зібралися порахувати розміри видимої частини Всесвіту. Вони стверджували, що для цього необхідно помножити 25 разів число 10 саме на себе. Оскільки для цього потрібно дуже багато місця, вони вимагали знести Палац алгоритму Евкіда, виставку чисел-близнюків та багато інших об'єктів. Хоча всім хотілося дізнатися, який же наш Всесвіт, але нікому не хотілося жертвувати такими класними і цінними спорудами. Було створено комісію, яка зайнялася пошуками необхідної вільної площі, але незабаром зайшла у глухий кут.

Несподівано положення Таблиця множення. Вона розповіла свою історію: - Мене вигадали для того, щоб не складати велику кількість однакових доданків. Адже тепер ніхто не пише 3+3+3+3+3+3+3, тепер записують 3х7. Це дуже економить місце. Давайте придумаємо щось схоже для множення.

І одразу придумали. Число множників стали записувати маленькою цифрою ззаду числа:

Всі вирази стали називати ступенем,кількість множників (маленьку цифру зверху) – показник ступеня, а сам множник – основа ступеня.

Не минуло й півгодини, як урочисто запровадили нову дію – зведення у ступінь, як країною чисел стали бігати 5 6 , 17 4 і ще. Але тільки бігати нецікаво, хочеться виконувати додавання, множення, віднімання, тобто вести себе як усі порядні числа. і ту виникли такі проблеми. Після введення дій необхідно встановити правила дійтак, щоб нікому не заважати і жодні закони не порушувати.

Спочатку спробували виконувати додавання, відкрили зведення законів і нічого не знайшли. Про віднімання навіть думати не стали, а множення пішло дуже легко, адже будь-який ступінь виходить з множників, отже, якщо взяти однакові підстави ступеня, то

Відразу записали у зведення законів нове правило:

При множенні ступенів з однаковим основа основа залишається незмінною, а показники складають

Із розподілом виникли проблеми. Всім здавалося, що якщо розподіл дію зворотний у виноженні, то приділенні треба показники віднімати, але якщо , а якщо . Тоді ухвалили (під впливом консервативної меншини), що

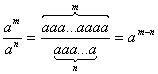, якщо m>n, і якщо n>m.

Провести перевірку нових правил запропонували 6 5 і 6 3: , а

При розподілі ступенів з однаковими підставами показники віднімаються . а цілком правило сформулювати важко.

Розібралися також зі ступенями з різними основами та однаковими показниками. На допомогу прийшли пересувний і сполучний закони: тому що ;

Щоб помножити ступеня з однаковими показниками, треба перемножити підстави, а показник залишити без зміни.

Щоб розділити ступеня з динаковими основами треба розділити основи, а показник залишити без зміни.

Виявилося, що можна навіть зводити ступінь у ступінь.

Настало загальне свято. Особливо сподобалося скорочувати дроби, розкладаючи їх на множники:

Подарунок зробив розподільчий закон. Він запропонував як складати однакові ступені, наприклад, ,Тобто . можна складати коефіцієнти.

Якщо ж ступеня з однаковими підставами, але з різними коефіцієнтами, можна загальний множниквинести за дужку:

2) ступеня з негативним показником:

Усі вже звикли до дій зі ступенями з натуральними показникамими (їх так називають, тому що показники - натуральні числа).

І знайшлися незадоволені, ті хто не взяв участь у створенні нових чисел.

Всім відомо, що при відніманні може виходити 0, а також негативні числа, - говорили вони і організували рух на підтримку ступенів із негативним показником.

Як же може бути негативна кількість співмножників? - Здивувалися натуральні числа.

Треба визначити, це якраз підходить під ваше правило: .

А ступеня із негативним показником визначити, як (Z - - негативні цілі числа).

Наприклад,

Тоді формула для поділу ступенів стане просто

Добре, - сказали зберігачі Зводу законів, - тоді доведіть, що всі правила дій зі ступенями збережуться і за умови введення ступенів із негативним показниками.

Більше того, негативні числа запропонували план доказу всіх теорем, про дії зі ступенями.

1.В вираженні за визначенням замінити ступінь із негативним показником на ступінь із натуральним показником.

2.Виконати дії за правилами дій зі ступенями з натуральними показниками

3.За визначенням перейти від ступенів з натуральними показниками до ступенів з негативними показниками.

А також навели пояснювальні приклади: 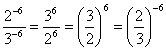, записувати можна коротше:

Отже, виявилося, що всі правила дій збереглися для ступенів із негативними показниками.

3) ступеня з дробовим показником:

при витягуванні кореня зі ступеня поділяють показник ступеня на показник кореня, якщо таке поділ виконається націло; наприклад: √ a 4 = a 2 , 3 √x 9 = x 3 і т. п. Умовимося тепер поширити це правило на ті випадки, коли показник ступеня не ділиться націло на показник кореня. Наприклад, ми умовимося приймати, що

Взагалі ми домовимося, що вираз означає корінь, показник якого є знаменником, а показник підкореного числа - чисельник дробового показника (Тобто. n √a m ).

Умовимося ще допускати і негативні дробові показники у тому сенсі, як ми допустили негативні цілі показники; наприклад, умовимося, що

Зауваження.Дробові показники були введені в алгебру головним чином голландським інженером Сімоном Стевіном на початку XVII століття Пізніше, наприкінці XVII століття, Оксфордський професор Джон Валліс ввів у вжиток негативні показники.

259. Основна властивість дробового показника. Величина ступеня з дробовим показником не зміниться, якщо ми помножимо або розділимо на те саме число (відмінне від нуля) чисельник і знаменник дробового показника. Так:

Справді, знаменник дробового показника означає показник кореня, а чисельник означає показник підкореного виразу, А такі показники, як ми бачили, можна множити і ділити на те саме число.

Виходячи з цієї властивості, ми можемо перетворювати дробовий показник так само, як і звичайний дріб : наприклад, ми можемо скорочувати дробовий показник, або наводити кілька дробових показників одного знаменника.

Від цілих показників ступеня числа a напрошується перехід до раціональних показників. Нижче ми визначимо ступінь з раціональним показником, причому це робитимемо так, щоб зберігалися всі властивості ступеня з цілим показником. Це необхідно, оскільки цілі є частиною раціональних чисел.

Відомо, що безліч раціональних чисел складається з цілих і дрібних чисел, причому кожне дробове числоможе бути представлено у вигляді позитивної або негативної звичайного дробу. Ступінь із цілим показником ми визначили у попередньому пункті, тому, щоб закінчити визначення ступеня з раціональним показником, потрібно надати сенс ступеня числа aз дробовим показником m/n, де m- ціле число, а n- Натуральне. Зробимо це.

Розглянемо ступінь із дробовим показником виду. Щоб зберігати силу властивість ступеня, повинна виконуватися рівність . Якщо врахувати отриману рівність і те, як ми визначили корінь n-ого ступеня, то логічно прийняти за умови, що за даними m, nі aвираз має сенс.

Неважко перевірити, що при справедливі всі характеристики ступеня з цілим показником (це зроблено в розділі якості ступеня з оптимальним показником).

Наведені міркування дозволяють зробити наступний висновок: якщо дані m, nі aвираз має сенс, то ступенем числа aз дробовим показником m/nназивають корінь n-ой міри з aу ступені m.

Це твердження впритул підводить нас до визначення ступеня з дрібним показником. Залишається лише розписати, за яких m, nі aмає сенс вираз. Залежно від обмежень, що накладаються на m, nі aіснують два основні підходи.

1. Найпростіше накласти обмеження на a, Прийнявши a≥0для позитивних mі a>0для негативних m(бо при m≤0ступінь 0 mне визначена). Тоді ми отримуємо наступне визначення ступеня з дрібним показником.

Визначення.

Ступенем позитивного числа aз дробовим показником m/n , де m- ціле, а n – натуральне число, називається корінь n-ой з числа aу ступені m, тобто, .

Також визначається дробовий ступінь нуля з тим лише застереженням, що показник має бути позитивним.

Визначення.

Ступінь нуля з дрібним позитивним показником m/n , де m- ціле позитивне, а n- натуральне число, визначається як .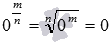
При ступінь не визначається, тобто ступінь числа нуль з дробовим негативним показником не має сенсу.

Слід зазначити, що за такого визначення ступеня з дробовим показником існує один нюанс: при деяких негативних aта деяких mі nвираз має сенс, а ми відкинули ці випадки, ввівши умову a≥0. Наприклад, мають сенс запису або , а дане вище визначення змушує нас говорити, що ступеня з дробовим показником виду немає сенсу, оскільки основа має бути негативним.

2. Інший підхід до визначення ступеня з дрібним показником m/nполягає в роздільному розгляді парних та непарних показниках кореня. Цей підхід потребує додаткової умови: ступінь числа a, показником якого є скоротитий звичайний дріб, вважається ступенем числа a, показником якого є відповідний нескоротний дріб (важливість цієї умови пояснимо трохи нижче). Тобто якщо m/n- Нескоротний дріб, то для будь-якого натурального числа kступінь попередньо замінюється на .

При парних nта позитивних mвираз має сенс за будь-якого неотрицательного a(корінь парного ступеняз негативного числане має сенсу), при негативних mчисло aмає бути ще відмінним від нуля (інакше буде поділ на нуль). А при непарних nта позитивних mчисло aможе бути будь-яким (корінь непарного ступеня визначено для будь-якого дійсного числа), а при негативних mчисло aмає бути відмінним від нуля (щоб був поділу на нуль).

Наведені міркування призводять нас до такого визначення ступеня з дрібним показником.

Визначення.

Нехай m/n- Нескоротний дріб, m- ціле, а n- натуральне число. Для будь-якого скоротливого звичайного дробу ступінь замінюється на . Степінь числа aз нескоротним дробовим показником m/n- це для

o будь-якого дійсного числа a, цілого позитивного mта непарного натурального n, наприклад, ;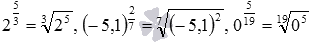

o будь-якого відмінного від нуля дійсного числа a, цілого негативного mта непарного n, наприклад, ;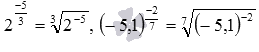

o будь-якого невід'ємного числа a, цілого позитивного mта парного n, наприклад, ;

o будь-якого позитивного a, цілого негативного mта парного n, наприклад, ;

o в інших випадках ступінь з дробовим показником не визначається, як, наприклад, не визначені ступеня .a

Розглянемо маленький приклад. Обчислимо 4√(5 12).

Скористаємося властивостями кореня та ступеня числа. 5 12 = (5 3) 4 , отже, можемо записати умову так:

• 4√((5 3) 4) = (4√(5 3)) 4 = 5 3 = 125.

Таким чином, отримуємо, що 4√(5 12) = 5 (12/4) . Також можна показати, що, наприклад,

• 5√(3 (-4)) = 3 (-4/3) .

Доведення

• Якщо n деяке натуральне число, причому n більше або дорівнює 2, m - деяке ціле число, і приватне m/n буде цілим числом, то при а >0 справедлива наступна рівність: n√(a m) = a (m/n).

Доведемо цей факт. m/n – деяке ціле число (за умовою), тобто у результаті розподілу ми отримаємо ціле k (m/n = k). Тоді можна записати, що m=k*n. Далі, застосовуючи властивості ступеня та арифметичного кореняотримаємо:

• n√(a m) = n√(a (n*k)) =n√((a k) n) = a k = a (m/n) .

Тобто n√(a m) = a(m/n) . Що й потрібно було довести.

Якщо ж при розподілі m на n вийде не ціле число, то ступінь виду a (m/n) , де а>0 визначають таким чином, щоб формула написана вище (n√(a m) = a (m/n)), залишалася вірною.

• Тобто формула n√(a m) = a (m/n) буде справедлива для будь-якого цілого числа m,кожного натурального числа n більше чи рівного двом і а>0.

Наприклад,

• 16 (3/4) = 4√(16 3) = 4√(2 12) = 2 3 = 8.
• 7 (5/4) = 4√(7 5) = 4√((7 4)*7) = 7*4√7.

Як ми знаємо, числа виду m/n, де n – деяке натуральне число, а m – деяке ціле число, називають дробовими чи раціональними числами.

З усього вищесказаного отримуємо, що ступінь визначено, для будь-якого раціонального показникаступеня та будь-якої позитивної основи ступеня.

Особливості

Варто зазначити, що якщо раціональне числоу показнику буде позитивним, то вираз n√(a m) матиме сенс не тільки за позитивних а, але й за рівного нуля.

• n√(0 m) = 0.

Тому, в математиці вважається, що з m/n > 0 виконується рівність 0 (m/n) = 0.

Зазначимо також, що при будь-якому цілому, будь-яких натуральних m і n, і позитивному а вірно наступна рівність:

a (m/n) = a ((mk)/(nk)).

Наприклад, 134 (3/4) = 134 (6/8) = 134 (9/12).