Звичайні та десяткові дроби

Кінцеві та нескінченні десяткові дроби

Кінцеві десяткові дроби

Множення та розподіл десяткових дробів на 10, 100, 1000, 10000 і т.д.

Перетворення кінцевого десяткового дробу в простий дріб

Десяткові дроби поділяються на три наступні класи: кінцеві десяткові дроби, нескінченні періодичні десяткові дроби та нескінченні неперіодичні десяткові дроби.

Кінцеві десяткові дроби

Визначення. Кінцевим десятковим дробом (десятковим дробом)називають дріб або змішане число, що має знаменник 10, 100, 1000, 10000 і т.д.

Наприклад,

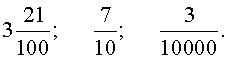
До десяткових дробів відносять також такі дроби, які можна призвести до дробів, що мають знаменник 10 , 100 , 1000 , 10000 і т.д., за допомогою основної властивості дробів .

Наприклад,

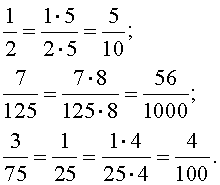
Твердження . Нескоротний простий дріб або нескоротне змішане неціле число є кінцевим десятковим дробом тоді і тільки тоді, коли розкладання їх знаменників на прості множники містить як множники лише числа 2 і 5, причому в довільних ступенях.

Для десяткових дробів існує спеціальний спосіб запису , використовуючи кому. Зліва від коми записується ціла частинадробу, а праворуч - чисельник дробової частини, перед яким дописується така кількість нулів, щоб число цифр після коми дорівнювало числу нулів у знаменнику десяткового дробу.

Наприклад,

Зауважимо, що десятковий дріб не зміниться, якщо приписати кілька нулів праворуч або ліворуч від нього.

Наприклад,

3,14 = 3,140 = 3,1400 = 003,14 .

Цифри, що стоять перед комою (ліворуч від коми) в десяткового запису кінцевого десяткового дробу, утворюють число, яке називають цілою частиною десяткового дробу.

Цифри, що стоять після коми (право від коми) у десятковому записі кінцевого десяткового дробу, називають десятковими знаками.

У кінцевому десятковому дробі кінцева кількість десяткових знаків. Десяткові знаки формують дробову частину десяткового дробу.

Множення та розподіл десяткових дробів на 10, 100, 1000 і т.д.

Для того щоб помножити десятковий дріб на 10, 100, 1000, 10000 і т.д., достатньо перенести кому вправо

Для того щоб розділити десятковий дріб на 10, 100, 1000, 10000 і т.д., достатньо перенести кому влівона 1, 2, 3, 4 тощо. десяткових знаків відповідно.

Наприклад,

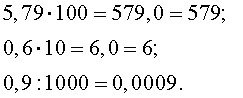
Повернення кінцевого десяткового дробу
у простий дріб

Звернення кінцевого десяткового дробу в простий дріб здійснюється дуже просто, наприклад,

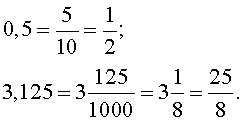
На нашому сайті можна також ознайомитися з розробленими викладачами навчального центру «Резольвента» навчальними матеріалами для підготовки до ЄДІ та ВДЕ (ДІА) з математики.

Для школярів, які бажають добре підготуватися та здати ЄДІ чи ОГЕ (ДІА) з математики або російської мовина високий бал, навчальний центр"Резольвента" проводить

У нас також для школярів організовано

Матеріал з Вікіпедії – вільної енциклопедії

$\backslash pm\; d\_m\; \backslash ldots\; d\_1\; d\_0(,)\; d\_(-1)\; d\_(-2)\; \backslash ldots$

$\backslash pm$ - знак дробу: або $+$, або $-$, $,$ - десяткова кома, що служить роздільником між цілою та дробовою частиною числа (стандарт країн СНД) Знак коми « $,$» - десяткова кома(Англ. decimal comma) - як роздільник цілої та дробової частин десяткового дробу прийнятий у Росії, європейських країнах(крім Великобританії та Ірландії) та багатьох інших країнах, на які вони мали культурний вплив. В англомовних країнах та країнах, на які вони мали вплив, для цього використовується знак точки « $.$» - десяткова точка(Англ. decimal point), а знак коми використовується для групування цифр цілої частини числа по три десяткові розряди (так званий роздільник груп розрядів, у Росії для цього використовується знак нерозривної прогалини""). Наприклад, дріб $\backslash frac(1~000~000)(3)$у десятковому записі в російському стандарті виглядатиме так: $\{333~333\{,\}333333\}(3)$, а в англійському стандарті так: $\{~333,333.333333(3)\}$. Докладніше див. Десятковий роздільник., $d\_k$- десяткові цифри. Причому послідовність цифр до коми(ліворуч від неї) кінцева (як мінімум одна цифра), а після коми(справа від неї) - може бути як кінцевою (зокрема, цифри після коми можуть взагалі бути відсутніми), так і нескінченною.

• $123\{,\}45$(кінцевий десятковий дріб)
• Подання числа $\backslash pi$у вигляді нескінченного десяткового дробу: $3\{,\}1415926535897...$

Значенням десяткового дробу $\backslash pm\; d\_m\; \backslash ldots\; d\_1\; d\_0,\; d\_(-1)\; d\_(-2)\; \backslash ldots$є дійсне число

$\backslash pm\; \backslash left\; (d\_m\; \backslash cdot\; 10^m\; +\; \backslash ldots\; +\; d\_1\; \backslash cdot\; 10^1\; +\; d\_0\; \backslash cdot\; 10^0\; +\; d\_(-1)\; \backslash cdot\; 10^(-1)\; +\; d\_(-2)\; \backslash cdot\; 10^(-2)\; +\; \backslash ldots\; \backslash right),$

Ця властивість була використана двічі у алгоритмі. На самому початку побудови вибиралося ціле $a\_0$, таке, що дійсне число $\backslash alpha$знаходиться між $a\_0$і наступним цілим $a\_0\; +\; 1$:

Проте існування такого цілого числа $a\_0$треба ще довести: не можна виключати, наприклад, можливість, коли, хоч би яке було ціле $n$, завжди має місце нерівність $n\; \backslash leqslant\; \backslash alpha$. Якби цей випадок мав місце, то, очевидно, потрібного числа $a\_0$не знайшлося б.

Ця можливість якраз виключається аксіомою Архімеда, згідно з якою б не було число $\backslash alpha$, завжди знайдеться ціле $n$таке, що $n\; >\; \backslash alpha$. Тепер серед чисел $k=\; 1,\; \backslash ldots,\; n$візьмемо найменше, що має властивість $k\; >\; \backslash alpha$. Тоді

Потрібне число знайдено: $a\_0\; =\; k-1$.

Вдруге аксіома Архімеда неявно використовувалася при доказі прагнення нулю довжин відрізків послідовності $I\_0,\; I\_1,\; I\_2,\; \backslash ldots$:

$\backslash lim\_(n\; \backslash to\; \backslash infty)\; 10^(-n)\; =\; 0$

Суворий доказ цієї пропозиції спирається на аксіому Архімеда. Доведемо еквівалентне співвідношення

$$

Відповідно до аксіоми Архімеда, яке б не було дійсне число $E\; >0$, послідовність натуральних чисел $1,\; 2,\; \backslash ldots$перевершить його, починаючи з деякого номера. А оскільки для кожного $n$має місце нерівність

$10^n\; >\; n$

то послідовність $10^n$також перевершить $E$починаючи з того ж номера. Відповідно до визначення межі числової послідовності, це означає, що $\backslash lim\_(n\; \backslash to\; \backslash infty)\; 10^(n)\; =\; \backslash infty$.

Неоднозначність уявлення у вигляді десяткового дробу

За допомогою наведеного алгоритму ми можемо для будь-якого дійсного числа $\backslash alpha$побудувати десятковий дріб, що представляє це число. Однак може статися, що це саме число $\backslash alpha$може бути представлено у вигляді десяткового дробу та іншим чином.

Неєдиність уявлення чисел у вигляді десяткових дробів вже випливає з того тривіального факту, що, приписуючи кінцевого дробу праворуч після коми нулі, ми отримуватимемо формально різні десяткові дроби, що становлять одне й те саме число.

Розглянемо, наприклад, десятковий дріб

$0(,)99\backslash ldots$

Згідно з визначенням, цей дріб є уявленням числа $0\; +\; 9/10\; +\; 9/100\; +\; \backslash ldots\; =\; 1$. Разом з тим, це число може бути представлене у вигляді десяткового дробу $1(,)00\backslash ldots$.

Цей приклад можна узагальнити. Можна показати, що дроби

$\backslash pm\; a\_0(,)a\_1\; \backslash ldots\; a\_(n-1)\; a\_n\; 999\; \backslash ldots$

$\backslash pm\; a\_0(,)a\_1\; \backslash ldots\; a\_(n-1)\; (a\_n+1)\; 000$

де $a\_n\; \backslash neq\; 9$, представляють те саме дійсне число.

Виявляється, цим загальним прикладом вичерпуються всі випадки неоднозначності уявлення дійсних чисел як десяткових дробів. При цьому ми, звичайно, не розглядаємо тривіальні випадки дробів, отриманими приписуванням нулів у кінець один одному, а також кілька дробів $+\; 0(,)00\; \backslash ldots$і $-\; 0(,)00\; \backslash ldots$.

Ці результати можна підсумувати у наступній теоремі.

Теорема. Будь-яке дійсне число $\backslash alpha$, не представлене у вигляді $p/10^s$, де $p$- ціле, $s$- ціле невід'ємне, допускає єдине уявлення у вигляді десяткового дробу; при цьому цей дріб є нескінченним.

Будь-яке дійсне число виду $\backslash alpha\; =\; p/10^s$може бути представлено у вигляді десяткового дробу більш ніж одним способом. Якщо $\backslash alpha\; \backslash neq\; 0$, то воно може бути представлене як у вигляді кінцевого десяткового дробу, а також нескінченного дробу, отриманого приписуванням нулів у кінець після коми, так і у вигляді нескінченного дробу, що закінчується на $999\; \backslash ldots$. Число $\backslash alpha\; =\; 0$може бути представлено дробами виду $+0(,)00\; \backslash ldots$, а також дробами виду $-0(,)00\; \backslash ldots$.

Зауваження. Нескінченні дроби, що закінчуються на $999\backslash ldots$, виходять, якщо у наведеному вище алгоритмі завжди вибирати лівий відрізокзамість правого.

Зайві нулі та похибка

Слід зазначити, що, з точки зору похибки, запис десяткового дробу з нулями в кінці не зовсім тотожний запису без цих нулів.

Вважають, що, якщо похибка не вказана, то абсолютна похибка десяткового дробу дорівнює плюс-мінус половині((#if:||

Інші приклади:

• «25» - абсолютна похибка дорівнює ±0,5 (також такий запис може означати точне значення 25: наприклад, 25 штук);
• "25,0" - абсолютна похибка дорівнює ±0,05;
• «25,00» - абсолютна похибка дорівнює ±0,005.

Періодичні десяткові дроби

Нескінченний десятковий дріб називається періодичної, якщо її послідовність цифр після коми, починаючи з деякого місця, являє собою групу цифр, що періодично повторюється. Іншими словами, періодичний дріб - десятковий дріб, що має вигляд

$\backslash pm\; a\_0,\; a\_1\; \backslash ldots\; a\_m\; \backslash underbrace(b\_1\; \backslash ldots\; b\_l)\; \backslash underbrace(b\_1\; \backslash ldots\; b\_l)\; \backslash ldots$

Такий дріб прийнято коротко записувати у вигляді

$\backslash pm\; a\_0,\; a\_1\; \backslash ldots\; a\_m\; (b\_1\; \backslash ldots\; b\_l)$

Група цифр, що повторюється $b\_1\; \backslash ldots\; b\_l$називається періодомдроби, кількість цифр у цій групі – довжиною періоду.

Якщо в періодичному дробі період слідує відразу після коми, то дріб називається чистої періодичної. Якщо між комою і першим періодом є цифри, дріб називається змішаної періодичної, а група цифр після коми до першого знаку періоду - передперіодомдроби. Наприклад, дріб $1(,)(23)\; =\; 1(,)2323\; \backslash ldots$є чистою періодичною, а дріб $0(,)1(23)=0(,)12323\; \backslash ldots$- Змішаної періодичної.

Основна властивість періодичних дробів, завдяки якому їх виділяють з усієї сукупності десяткових дробів, полягає в тому, що періодичні дроби і тільки вони є раціональними числами. Точніше, має місце таке речення.

Теорема. Будь-який нескінченний періодичний десятковий дріб представляє раціональне число. Назад, якщо раціональне число розкладається в нескінченний десятковий дріб, то цей дріб є періодичним.

Можна показати, що періодичні дроби відповідають раціональним числам, у запису яких у вигляді нескоротного дробу $p/q$знаменник $q$ не маєпростих дільників $2$і $5$, а також раціональним числам $p/q$, у яких знаменник $q$ має тількипрості дільники $2$і $5$. Відповідно, змішані періодичні дроби відповідають нескоротним дробам $p/q$, знаменник $q$яких має як прості дільники $2$або $5$, і відмінні від них.

Переведення з десяткового дробу до звичайного

Припустимо, що дано періодичний десятковий дріб $x=0(,)(1998)$з періодом 4. Зауважимо, що домноживши її на $10^4\; =\; 10000$, отримаємо великий дріб $10000x\; =\; 1998\; (,)\; (1998)$з тими самими цифрами після коми. Відібравши цілу частину, отримуємо ((#if:| ((#ifeq:((#invoke:String|sub|(((автор)))|-1))| |(((автор)))|((#ifeq:((#invoke:String|sub|) (((автор)))|-6|-2))| |(((автор)))|((#ifeq:((#invoke:String|sub|(((автор))))|-6 |-2)) | / span | Шаблон: ±.| Шаблон: ±. ))))))))((#if: |((#if: |[(((посилання частина))) (((частина)))]| (((частина))))) // ))((#if: |[[:s:(((вікітека)))|Енциклопедія для дітей ]]|((#if: |[]|((#if:|[(((посилання))) Енциклопедія для дітей ]|Енциклопедія для дітей) дітей ))))))((#if:| = (((оригінал))) ))((#if:| / (((відповідальний))).|((#if:||.))) )((#if:Енциклопедія для дітей |((#if:| ((#if:| = (((оригінал2))) ))((#if:| / ((відповідальний2)))). #if:||.))))))))((#if:| - (((видання))).))((#switch:((#if:М.|м))((# if:Аванта+|і))((#if:2001|г))

|мг= - Шаблон:Вказівка ​​місця у бібліосилці : Аванта+, 2001. |ми= - Шаблон:Вказівка ​​місця у библиотеке : Аванта+. |мг= - Шаблон:Вказівка ​​місця у библиотеке , 2001. |иг= - Аванта+, 2001. |м= - Шаблон:Вказання місця у библиотеке |і= - Аванта+. |г= - 2001. |

))((#if:| - (((тому як є))).))((#if:11. Математика|((#if: | [(((посилання тому))) - Т. 11). Математика.]| - Т. 11. Математика.))))((#if:| - Vol. (((volume))).))((#if:| - Bd. (((band))) .))((#if:| - (((сторінки як є))).))((#if:| - С. ((#if:|[(((сторінки)))) (стб.) ((стовпці)))).|((((сторінки))).))))((#if:| - (((сторінок як є))))))((#if:| - (( сторінок))) с.))((#if:| - P. ((#if:|[(((pages))))] (col. (((columns)))).|(((pages) )).))))((#if:| - S. ((#if:|[(((seite)))]) (Kol. (((kolonnen)))).|(((seite)) ).))))((#if:| - p.))((#if:| - S.))((#if:| - ((((серія))))))((# if:| - (((тираж))) прим. ))((#if:5-8483-0015-1| - ISBN 5-8483-0015-1 .))((#if:| - ISBN (( (isbn2))).))((#if:| - ISBN (((isbn3))).))((#if:| - ISBN (((isbn4))).))((#if:| - ISBN (((isbn5))).))((#if:| - DOI :(((doi)))) ((#ifeq:Шаблон:Str left |10.|| [ Помилка: Неправильний DOI!] ((#if:||)))))), сторінка 179: $10000x-1998=x\; \backslash Rightarrow\; x=\backslash frac(1998)(9999)=\backslash frac(222)(1111)$

Вимова десяткових дробів

У російській мові десяткові дроби читаються так: спочатку вимовляється ціла частина, потім слово «цілих» (або «ціла»), потім дробова частина так, ніби все число складалося тільки з цієї частини, тобто чисельник дробу - кількісне числівник жіночого роду (одна, дві, вісім тощо. буд.), а знаменник - порядкове числове (десята, сота, тисячна, десятитисячна тощо. буд.).

Наприклад: 5,45 – п'ять цілих, сорок п'ять сотих.

Для більш довгих чисел іноді десяткову частину розбивають за ступенями тисячі. Наприклад: 0,123456 - нуль цілих, сто двадцять три тисячних, чотириста п'ятдесят шість мільйонних.

Однак на практиці часто як раціональніше, превалює така вимова: ціла частина, союз «і» (часто опускається), дробова частина.

Наприклад: 5,45 - п'ять та сорок п'ять; (П'ять-сорок п'ять).

Для періодичних десяткових дробів вимовляють частину числа до періоду (виражену цілим числом у разі чистого періодичного дробу або кінцевим десятковим дробом у разі змішаного періодичного дробу), а потім додають число в періоді. Наприклад: 0,1(23) - нуль цілих, одна десята та двадцять три в періоді; 2, (6) - дві цілих та шість у періоді.

Історія

Десяткові дроби вперше зустрічаються в Китаї приблизно з ІІІ століття н. е. при обчисленнях на лічильній дошці (суаньпань). У письмових джерелах десяткові дроби ще деякий час зображували у традиційному (не позиційному) форматі, але поступово позиційна система витіснила традиційну Jean-Claude Martzloff. A History of Chinese Mathematics. Springer. 1997. ISBN 3-540-33782-2..

Перський математик і астроном Джамшид Гіяс-ад-дин аль-Каші (1380-1429) у трактаті «Ключ арифметики» оголосив себе винахідником десяткових дробів, хоча вони зустрічалися в працях Ал-Уклідісі, який жив на 5 століть раніше ((#if:Berggren J. Lennart.| ((#ifeq:((#invoke:String|sub|Berggren J. Lennart.|-1))| |Berggren J. Lennart.|((#ifeq:((#invoke:String|sub|Berggren J. Lennart) .|-6|-2))| |Berggren J. Lennart.|((#ifeq:((#invoke:String|sub|Berggren J. Lennart.|-6|-2))|/span|Шаблон :±.| Шаблон: ±. ))))))))((#if: Mathematics in Medieval Islam|((#if: |[(((посилання частина))) Mathematics in Medieval Islam)) // ))((#if:|[ [:s:(((вікітека)))|The Mathematics of Egypt, Mesopotamia, China, India, та Islam: A Sourcebook]]|((#if: |

Щоб покрити числову вісь скрізь щільною множиною точок, немає необхідності використовувати всюсукупність раціональних чисел: достатньо, наприклад, обмежитися лише тими числами, що виникають при підрозділі одиничного відрізка на 10, потім на 100, 1000 і т. д. рівних частин. Отримані при цьому точки розподілу відповідають "десятковим дробам". Так, числу відповідає точка, розташована в першому одиничному інтервалі, у другому "підінтервалі" довжини 10 -1 і саме вона є початкова точка третього "підпідінтервалу" довжини 10 -2

(а -n означає). Якщо такого роду десятковий дріб містить п знаків після коми, то він має вигляд:

f = z + a 1 * 10 -1 + a 2 * 10 -2 + a 3 * 10 -3 + ... + a n * 10 -n.

де z- ціле число, а коефіцієнти а- цифри 0, 1, 2, ..., 9, що позначають число десятих, сотих і т. д. Скорочено число fзаписується в десятковій системі наступним чином: z, а 1, а 2, a 3 ... a n.Ми переконуємося безпосередньо, що такі десяткові дроби може бути представлені у вигляді звичайних дробів , де q = 10 n ; так, наприклад, Якщо виявиться, що p і q мають загальний множникто дроб можна скоротити, і тоді знаменник буде деяким дільником числа 10 n . З іншого боку, нескоротний дріб, у якого знаменник не є дільник деякою мірою 10, не може бути представлений у вигляді десяткового дробу зазначеного типу. Наприклад, але не може бути написана як десятковий дріб з кінцевим числом n десяткових знаків, хоч би як було велике n: насправді, з рівності виду

варто було б

10 n = 3b,

а остання рівність неможлива, тому що 3 не входить множником ні в яку міру числа 10.

Візьмемо тепер на числовій осі якусь точку Р, яка не відповідає жодному кінцевому десятковому дробу; можна, наприклад,

взяти раціональну точку або ірраціональну точку √2. Тоді в процесі послідовного підрозділу одиничного інтервалу на 10 рівних частин точка Р ніколи не виявиться в числі точок розподілу: вона буде знаходитися всередині десяткових інтервалів, довжина яких необмежено зменшуватиметься; кінці цих інтервалів відповідають кінцевим десятковим дробам і наближають точку Р з будь-яким ступенем точності. Розглянемо дещо докладніше цей процес наближення.

Припустимо, що точка Р лежить у першому одиничному інтервалі. Зробимо підрозділ цього інтервалу на 10 рівних частин, кожна довжини 10 -1 і припустимо, що точка Р потрапляє, скажімо, в третій з цих інтервалів. На цій стадії ми можемо стверджувати, що Р укладена між десятковими дробами 02 і 03. Поділяємо знову інтервал від 0,2 до 0,3 на 10 рівних частин, кожна довжини 10 -2 і виявимо, що Р потрапляє, припустимо, в четвертий з цих інтервалів. Поділяючи його, як раніше, бачимо, що точка Р потрапляє в перший інтервал довжини 10 -3. Тепер можна сказати, що точка Р укладена між 0,230 та 0,231. Цей процес може бути продовжений до нескінченності і призводить до нескінченної послідовності цифр а 1 , а 2 , а 3 , ... , а n , ... , яка має таку властивість: як би не було n, точка Р укладена в інтервалі I n , У якого початкова точка є 0, а 1 а 2 а 3 ... n-1 а n , а кінцева - 0, а 1 а 2 а 3 ... а n-1 (а n + 1), причому довжина I n дорівнює 10-n. Якщо будемо вважати по порядку n = 1,2, 3, 4,..., то побачимо, що кожен з інтервалів I 1 , I 2 , I 3 ... міститься в попередньому, причому їх довжини 10 -1 , 10 -2, 10 -3, ... необмежено зменшуються. Ми скажемо, коротше, що точка Р укладена в стягується послідовність десяткових інтервалів.Наприклад, якщо точка Р є , всі цифри а 1 , а 2 , а 3 ,... рівні 3, і Р укладена будь-якому інтервалі I n від 0,333 ... 33 до 0,333 ... 34, тобто. більше, ніж 0,333...33, і менше, ніж 0,333...34, хоч би скільки взяти цифр після коми. Ми скажемо в цих обставинах, що n-значний десятковий дріб 0,333...33" прагне до , коли число цифр n необмежено зростає. І ми умовимося писати

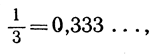
причому точки означають, що десятковий дріб може бути продовжений "до нескінченності".

Ірраціональна точка √2, яка була розглянута у пункті 1, також призводить до нескінченного десяткового дробу. Але закон, якому підпорядковуються послідовні цифри десяткового розкладання, цього разу не є очевидним. Ми не можемо вказати формулу, яка давала б цифру, що стоїть на n-му місці, хоча можна обчислити стільки цифр, скільки ми побажали собі заздалегідь призначити:

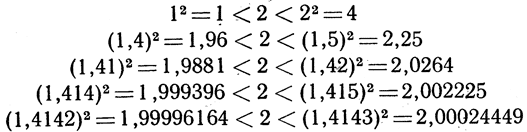
Як загальне визначення ми скажемо, що точка Р, яка не може бути представлена ​​у вигляді десяткового дробу з кінцевим числом десяткових знаків, представляється у вигляді нескінченного десяткового дробу z, а 1 а 2 а 3 ...,якщо, як би не було n, точка Р лежить в інтервалі довжини 10"" з початковою точкою z, a 1 а 2 а 3 ... а n.

Таким чином, ми встановлюємо відповідність між усіма точками числової осі та всіма (кінцевими та нескінченними) десятковими дробами. Тепер ми спробуємо запровадити попереднє визначення: "число" є кінцевий або нескінченний десятковий дріб.Ті нескінченні десяткові дроби, які не становлять раціонального числа, називаються ірраціональними числами.До середини XIX століттяміркування, подібні до наведених вище, здавались достатніми для пояснення того, як влаштована система раціональних та ірраціональних чисел - числовий континуум.Надзвичайні успіхи математики, досягнуті починаючи з XVII століття, зокрема розвиток аналітичної геометрії та диференціального та інтегрального обчислень, твердо базувалися саме на такому уявленні про систему чисел. Однак "в період критичного перегляду принципів і консолідації результатів стало відчуватися все більш і більш виразно, що поняття ірраціонального числаповинно бути більш точному і глибокому аналізу. Але, перш ніж перейти до нарису сучасної теорії числового континууму, нам доведеться розглянути та розібрати – на більш-менш інтуїтивній основі – одне з математичних понять капітальної значущості – поняття межі.

Вправа. Обчислити приблизно і з помилкою, що не перевищує 10 -2.

Відомо, що якщо знаменник пнескоротного дробу у своєму канонічному розкладі має простий множник не рівний 2 і 5, то цей дріб не уявний у вигляді кінцевого десяткового дробу. Якщо спробуємо у разі записати вихідну нескоротний дріб як десяткової, виробляючи розподіл чисельника на знаменник, то процес розподілу закінчитися неспроможна, т.к. у разі його завершення через кінцеве число кроків ми отримали б у приватному кінцевий десятковий дріб, що суперечить раніше доведеній теоремі. Так що в цьому випадку десятковий записпозитивного раціонального числа а= представляється нескінченним дробом.

Наприклад, дріб = 0,3636. Легко помітити, що залишки при розподілі 4 на 11 періодично повторюються, отже, і десяткові знаки періодично повторюватимуться, тобто. виходить нескінченний періодичний десятковий дріб, Яку можна записати так 0,(36).

Періодично повторювані цифри 3 і 6 утворюють період. Може виявитися, що між комою та початком першого періоду стоїть кілька цифр. Ці цифри утворюють передперіод. Наприклад,

0,1931818... Процес розподілу 17 на 88 нескінченний. Цифри 1, 9, 3 утворюють передперіод; 1, 8 – період. Розглянуті нами приклади відбивають закономірність, тобто. будь-яке позитивне раціональне число є або кінцевим, або нескінченним періодичним десятковим дробом.

Теорема 1.Нехай звичайний дріб нескоримий і в канонічному розкладі знаменника nє простий множник відмінний від 2 і 5. Тоді звичайний дріб представимо нескінченним періодичним десятковим дробом.

Доведення. Ми вже знаємо, що процес розподілу натуральної кількості mна натуральне число nбуде нескінченним. Покажемо, що вона буде періодичною. Справді, при розподілі mна nотримуватимуться залишки, менші n,тобто. числа виду 1, 2, ..., ( n– 1), звідки видно, що кількість різних залишків звичайно і тому, починаючи з деякого кроку якийсь залишок повториться, що спричинить повторення десяткових знаків приватного, і нескінченний десятковий дріб стає періодичним.

Мають місце ще дві теореми.

Теорема 2.Якщо розкладання знаменника нескоротного дробу на прості множники не входять цифри 2 і 5, то при перетворенні цього дробу в нескінченний десятковий дріб вийде чистий періодичний дріб, тобто. дріб, період якого починається відразу після коми.

Теорема 3.Якщо ж до розкладання знаменника входять множники 2 (або 5) або той і інший, то нескінченний періодичний дріб буде змішаним, тобто. між комою та початком періоду буде кілька цифр (передперіод), а саме стільки, який більший із показників ступенів множників 2 та 5.

Теореми 2 та 3 пропонується довести читачеві самостійно.

28. Способи переходу від нескінченних періодичних
десяткових дробів до дробів звичайних

Нехай даний періодичний дріб а= 0(4), тобто. 0,4444.

Помножимо ана 10, отримаємо

10а= 4,444…4…Þ 10 а = 4 + 0,444….

Тобто. 10 а = 4 + а, отримали рівняння щодо а, Вирішивши його, отримаємо: а= 4 Þ а = .

Помічаємо, що 4 – одночасно і чисельник отриманого дробу та період дробу 0,(4).

Правилозвернення до звичайний дрібчистого періодичного дробу формулюється так: чисельник дробу дорівнює періоду, а знаменник складається з такої кількості дев'яток, скільки цифр у періоді дробу.

Доведемо тепер це правило для дробу, період якого складається з п

а=. Помножимо ана 10 n, отримаємо:

10n × а = = + 0, ;

10n × а = + a;

(10n – 1) а = Þ a = =.

Отже, сформульоване раніше правило, доведено для будь-якого чистого періодичного дробу.

Нехай тепер дано дріб а= 0,605 (43) - змішана періодична. Помножимо ана 10 із таким показником, скільки цифр у передперіоді, тобто. на 10 3 отримаємо

10 3 × а= 605 + 0,(43) Þ 10 3 × а = 605 + = 605 + = = ,

тобто. 10 3 × а= .

Правилозвернення в звичайний дріб змішаного періодичного дробу формулюється так: чисельник дробу дорівнює різниці між числом, записаним цифрами, що стоять до початку другого періоду, і числом, записаним цифрами, що стоять до початку першого періоду, знаменник складається з такої кількості дев'яток, скільки цифр у періоді і такого числа нулів скільки цифр коштує на початок першого періоду.

Доведемо тепер це правило для дробу, передперіод якого складається з пцифр, а період із доцифр. Нехай даний періодичний дріб

Позначимо в= ; r= ,

з= ; тоді з=в × 10до + r.

Помножимо ана 10 із таким показником ступеня скільки цифр у передперіоді, тобто. на 10 n, отримаємо:

а×10 n = + .

Враховуючи введені вище позначення, запишемо:

а× 10n= в+ .

Отже, сформульоване вище правило доведено для будь-якого змішаного періодичного дробу.

Будь-який нескінченний періодичний десятковий дріб є формою запису деякого раціонального числа.

З метою одноманітності іноді кінцевий десятковий дріб також вважають нескінченним періодичним десятковим дробом з періодом «нуль». Наприклад, 0,27 = 0,27000...; 10,567 = 10,567000 ...; 3 = 3000 ... .

Тепер стає справедливим таке твердження: всяке раціональне число можна (і до того ж єдиним чином) висловити нескінченною десятковою. періодичним дробомі всякий нескінченний періодичний десятковий дріб виражає рівно одне раціональне число (періодичні десяткові дроби з періодом 9 при цьому не розглядаються).