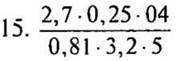Чисельник виразу перетворимо знаменник

Ціле вираз - це математичне вираз, складене з чисел і літерних змінних за допомогою дій складання, віднімання та множення. Також до цілих відносяться висловлювання, які мають у своєму складі розподіл на якесь число, відмінне від нуля.

Приклади цілого виразу

Нижче наведено кілька прикладів цілих виразів:

1. 12 * a ^ 3 + 5 * (2 * a -1);

3. 4*y- ((5*y+3)/5) -1;

Дробові вирази

Якщо ж у виразі присутній розподіл на змінну або інше вираз містить змінну, то такий вираз не є цілим. Такий вираз називається дробовим. Дамо повне визначення дробового виразу.

Дробне вираз - це математичне вираз, яке крім дій додавання, віднімання та множення, виконаних з числами та буквеними змінними, а також поділу на число не рівне нулю, містить так само поділ на вирази з буквеними змінними.

Приклади дробових виразів:

1. (12 * a ^ 3 +4) / a

3. 4*x- ((5*y+3)/(5-y)) +1;

Дробові та цілі вирази становлять дві великі множини математичних виразів. Якщо ці множини об'єднати, то отримаємо нову множину, яка називається раціональними виразами. Тобто раціональні висловлюванняце все цілий і дрібні вирази.

Нам відомо, що цілі вирази мають сенс за будь-яких значень змінних, які до нього входять. Це випливає з того, що для знаходження значення цілого виразу необхідно виконувати дії, які завжди можливі: додавання, віднімання, множення, розподіл на число відмінне від нуля.

Дробні ж висловлювання, на відміну від цілих, можуть не мати сенсу. Так як присутня операція поділу на змінну або вираз містить змінні, і цей вираз може звернутися в нуль, а ділити на нуль не можна. Значення змінних, у яких дробове вираз матиме сенс, називають допустимими значеннями змінних.

Раціональний дріб

Одним з окремих випадків раціональних виразів буде дріб, чисельник і знаменник якого багаточлени. Для такого дробу в математиці теж існує своя назва – раціональний дріб.

Раціональний дріб матиме сенс у тому випадку, якщо його знаменник не дорівнює нулю. Тобто допустимими будуть всі значення змінних, у яких знаменник дробу відмінний від нуля.

Так як дріб дорівнює частці 2: 3, то і приватне від розподілу одного виразу на інше можна записати за допомогою риси. Наприклад, вираз (41,3 - 4,4): (15,3 + 33,9) можна записати так: Виконавши зазначені дії, знайдемо значення цього виразу: 0,75 або

• Частка двох чисел або виразів, у якому знак розподілу позначений рисою, називають дробовим виразом.

Наприклад, 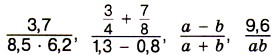- Дробові вирази.

Вираз, що стоїть над межею, називають чисельником, А вираз, що стоїть під межею, - знаменником дробового виразу. Чисельником та знаменником дробового виразу можуть бути будь-які числа, а також числові або буквені вирази.

З дробовими виразамиможна виконувати дії за тими самими правилами, що й із звичайними дробами.

приклад 1.Знайдемо значення виразу

Розв'язання. Помноживши чисельник і знаменник цього дробового виразу на 6, отримаємо:

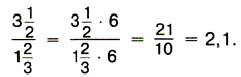
приклад 2.Знайдемо твір

Приклад 3.Знайдемо суму

При додаванні дробових виразів зручніше спочатку уявити їх у вигляді звичайних дробів, а потім вже виконувати додавання:

Який вираз називають дробовим?
Як називають вираз, що знаходиться над межею? під межею?

692. Назвіть чисельник та знаменник виразу:

693. Напишіть дробовий вираз, чисельник якого 3а – 2b, а знаменник – 6,7х + у.

694. Запишіть у вигляді дробового виразу:

(3,8 4,5 - 0,7): (6,3: 2,1 - 2,6).

Знайдіть значення цього виразу.

695. Знайдіть значення виразу:

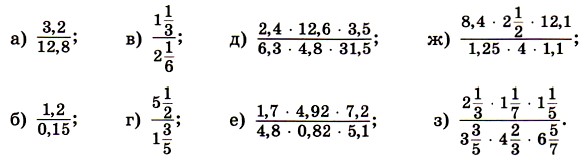
696. Виконайте дію:

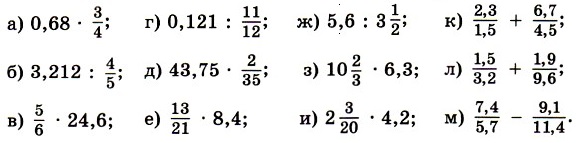
697. Виконайте дії:

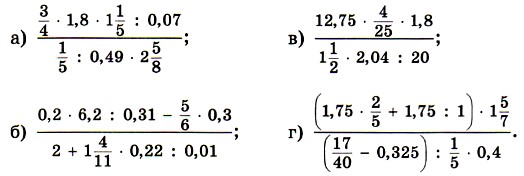
698. Знайдіть значення виразу якщо:

699. Знайдіть значення виразу, якщо:

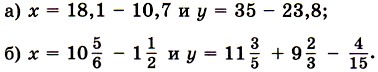
700. Знайти за допомогою мікрокалькулятора значення виразу можна за програмою:

а значення виразу за такою програмою:

Виконайте обчислення за цими програмами.

Побудуйте програму знаходження значення виразу та виконайте за нею обчислення:

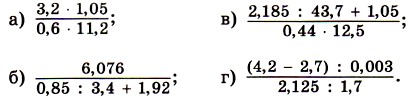
701. Обчисліть усно:

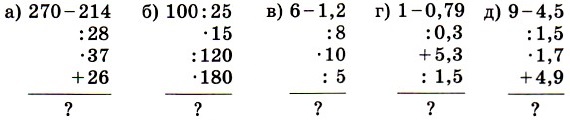
702. На координатному промені зазначені числа а та b (рис. 30). Чи можна вказати на промені точку з координатою

703. Обчисліть:

704. Знайдіть добуток дробів і добуток дробів, обернених даним. Яку властивість мають ці два твори? Перевірте припущення ще на одному прикладі. Доведіть цю властивість у загальному вигляді (за допомогою літерних виразів).

705. Знайдіть найбільше та найменше значення виразу якщо

706. Складіть задачу за рівнянням:

707. Ваня та Таня мали зустрітися на станції, щоб разом поїхати потягом, який відправляється о 8 год ранку. Ваня думає, що його годинник поспішає на 35 хв, хоча насправді він відстає на 15 хв. А Таня думає, що її годинник відстає на 15 хв, хоча він насправді поспішає на 10 хв. Що станеться, якщо кожен з них, покладаючись на свій годинник, прагнутиме прийти за 5 хв до відходу поїзда?

708. Вік Сергія становить вік батька. Сергію 12 років. Скільки років батькові?

709. Комбайнер за 1 год скосив пшеницю з площі 3 га, що становить 15% від того, що він скосив за день. Яку площу скосив комбайнер за день?

710. Груші становлять 25% усіх дерев саду, решта 150 дерев – яблуні. Скільки грушевих дерев у саду?

711. Площа 60 га становить 0,75 площі поля. Чому дорівнює площа поля?

712. Знайдіть число, якщо:

713. Ділянка землі, площа якої 6 а, складає сади, а площа саду становить усю присадибну ділянку. Чому дорівнює площа всієї присадибної ділянки?

714. За планом бригада має відремонтувати за місяць 25% дороги між двома селищами. За перший тиждень відремонтували 2 км 100 м-коду дороги, що склало 30% місячного плану. Яка довжина усієї дороги між селищами?

715. Розв'яжіть задачу:

1) У книзі 240 сторінок. У суботу хлопчик прочитав 7,5% усієї книги, а в неділю – на 12 сторінок більше. Скільки сторінок йому лишилося прочитати?
2) Для птахоферми заготовили 2600 т корми. Першого місяця було витрачено 8,5% корму, тоді як у другий місяць - на 30 т більше. Скільки тонн корму лишилося?

716. Знайдіть значення виразу:

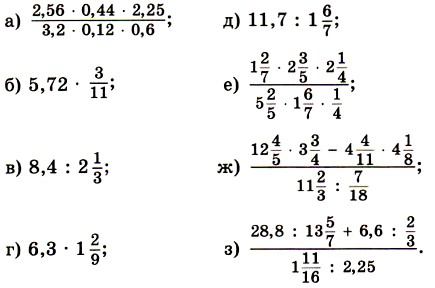
717. Нападники Коля та Микита під час баскетбольного матчу принесли своїй команді всіх очок. Скільки очок набрала за матч ця команда, якщо Коля набрав на 7 очок більше ніж Микита?

718. Потяг, що йде зі швидкістю 68 км/год, проходить відстань між містами за 6 год. Який час знадобиться велосипедисту, щоб проїхати цієї відстані зі швидкістю 17 км/год?

719. Отримали сплав зі шматка міді об'ємом 15 см 3 і шматка цинку об'ємом 10 см 3 . Яка маса 1 см 3 сплаву, якщо маса 1 см 3 міді 8,9 г, а маса 1 см 3 цинку 7,1 г? Отриманий результат округліть до десятих частин грама.

720. Кухня 10 м 2 становить 0,4 всіх нежитлових приміщень квартири. Площа нежитлових приміщень складає площу всієї квартири. Знайдіть площу усієї квартири.

721. Виріжте із щільного паперу фігури, зображені на малюнку 31, і склейте фігури, зображені на малюнку 32. Ці фігури називають призмами. У прямої призми бічні грані – прямокутники, а верхня та нижня основи – рівні багатокутники. На малюнку 32 а зображена трикутна призма, а на малюнку 32,6 - чотирикутна. Кожен прямокутний паралелепіпед – це чотирикутна призма.

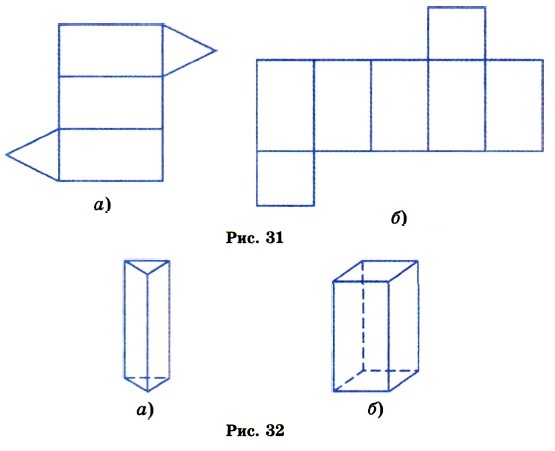
Будь-яке дробове вираз (п. 48) можна записати у вигляді , де Р і Q - раціональні вирази, причому Q обов'язково містить змінні. Такий дріб - називають раціональним дробом.

Приклади раціональних дробів:

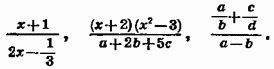
Основна властивість дробу виражається тотожністю справедливою за умов тут - ціле раціональне вираження. Це означає, що чисельник і знаменник раціонального дробу можна помножити чи розділити одне й те відмінне від нуля число, одночлен чи многочлен.

Наприклад, властивість дробу може бути використана для зміни знаків членів дробу. Якщо чисельник і знаменник дробу – помножити на -1, отримаємо Таким чином, значення дробу не зміниться, якщо одночасно змінити знаки у чисельнику та знаменника. Якщо ж змінити знак лише у чисельника чи тільки у знаменника, то й дріб змінить свої знак:

Наприклад,

60. Скорочення раціональних дробів.

Скоротити дріб - це означає розділити чисельник та знаменник дробу на загальний множник. Можливість такого скорочення обумовлена ​​основною властивістю дробу.

Щоб скоротити раціональний дріб, потрібно чисельник і знаменник розкласти на множники. Якщо виявиться, що чисельник та знаменник мають спільні множники, то дріб можна скоротити. Якщо спільних множниківні, то перетворення дробу за допомогою скорочення неможливе.

приклад. Скоротити дріб

Рішення. Маємо

Скорочення дробу виконано за умови.

61. Приведення раціональних дробів до спільного знаменника.

Загальним знаменником кількох раціональних дробів називається цілий раціональний вираз, який поділяється на знаменник кожного дробу (див. п. 54).

Наприклад, загальним знаменником дробів і служить многочлен оскільки він ділиться і на і багаточлен і многочлен і многочлен тощо. буд. Зазвичай беруть такий спільний знаменник, що будь-який інший спільний знаменник ділиться на Еібранний. Такий найпростіший знаменник іноді називають найменшим загальним знаменником.

У розглянутому вище прикладі загальний знаменник дорівнює Маємо

Приведення цих дробів до спільному знаменникудосягнуто шляхом множення чисельника та знаменника першого дробу на 2. а чисельника та знаменника другого дробу на Багаточлени називаються додатковими множниками відповідно для першого та другого дробу. Додатковий множник для даного дробу дорівнює частці від поділу загального знаменника на знаменник даного дробу.

Щоб кілька раціональних дробів привести до спільного знаменника, потрібно:

1) розкласти знаменник кожного дробу на множники;

2) скласти спільний знаменник, включивши в нього як співмножники всі множники отриманих у п. 1) розкладів; якщо деякий множник є у кількох розкладаннях, він береться з показником ступеня, рівним найбільшому з наявних;

3) знайти додаткові множники для кожного з дробів (для цього спільний знаменник ділять на знаменник дробу);

4) домноживши чисельник і знаменник кожного дробу на додатковий множник, привести дроб до загального знаменника.

приклад. Привести до спільного знаменника дробу

Рішення. Розкладемо знаменники на множники:

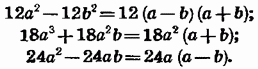
До загального знаменника треба включити такі множники: і найменше загальне кратне чисел 12, 18, 24, тобто . Отже, спільний знаменник має вигляд

Додаткові множники: для першого дробу для другого для третього Значить отримуємо:

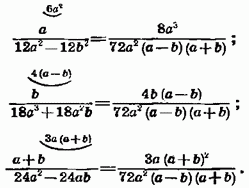
62. Додавання та віднімання раціональних дробів.

Сума двох (і взагалі будь-якого кінцевого числа) раціональних дробів з однаковими знаменникамитотожно дорівнює дробу з тим же знаменником і з чисельником, рівним сумічисельників дробів, що складаються:

Аналогічно справа у разі віднімання дробів з однаковими знаменниками:

Приклад 1. Спростити вираз

Рішення.

Для складання або віднімання раціональних дробів з різними знаменникамипотрібно насамперед привести дроби до спільного знаменника, та був виконати операції над отриманими дробами з однаковими знаменниками.

Приклад 2. Спростити вираз

Рішення. Маємо

63. Множення та розподіл раціональних дробів.

Добуток двох (і взагалі будь-якого кінцевого числа) раціональних дробів тотожно дорівнює дробу, чисельник якого дорівнює творучисельників, а знаменник - твору знаменників дробів, що перемножуються:

Приватне від розподілу двох раціональних дробів тотожно дорівнює дробу, чисельник якого дорівнює добутку чисельника першого дробу на знаменник другого дробу, а знаменник - добутку називника першого дробу на чисельник другого дробу:

Сформульовані правила множення та поділу поширюються і на випадок множення або поділу на многочлен: достатньо записати цей багаточлен у вигляді дробу зі знаменником 1.

Враховуючи можливість скорочення раціонального дробу, отриманого в результаті множення або поділу раціональних дробів, зазвичай прагнуть до виконання цих операцій розкласти на множники чисельники та знаменники вихідних дробів.

Приклад 1. Виконати множення

Рішення. Маємо

Використовуючи правило множення дробів, отримуємо:

Приклад 2. Виконати поділ

Рішення. Маємо

Використовуючи правило розподілу, отримуємо:

64. Зведення раціонального дробу на цілий ступінь.

Щоб звести раціональний дріб - натуральний ступінь, потрібно звести в цей ступінь окремий чисельник і знаменник дробу; перший вираз – чисельник, а другий вираз – знаменник результату:

Приклад 1. Перетворити на дріб ступінь 3.

Рішення Рішення.

При зведенні дробу в цілу негативний ступіньвикористовується тотожність справедливе за всіх значеннях змінних, у яких .

Приклад 2. Перетворити на дріб вираз

65. Перетворення раціональних виразів.

Перетворення будь-якого раціонального виразу зводиться до складання, віднімання, множення та поділу раціональних дробів, а також до зведення дробу в натуральний ступінь. Будь-який раціональний вираз можна перетворити на дріб, чисельник і знаменник якої - цілі раціональні вирази; у цьому, зазвичай, полягає мета тотожних перетворень раціональних выражений.

приклад. Спростити вираз

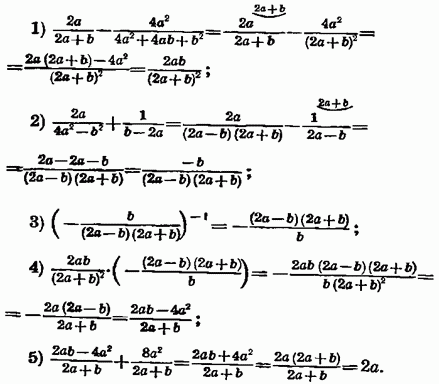
66. Найпростіші перетворення арифметичних коренів (радикалів).

При перетворенні арифметичної корії використовуються їх властивості (див. п. 35).

Розглянемо кілька прикладів застосування властивостей арифметичних коренівдля найпростіших перетворень радикалів. При цьому всі змінні вважатимемо такими, що приймають тільки невід'ємні значення.

Приклад 1. Вийняти корінь із твору

Рішення. Застосувавши властивість 1°, отримаємо:

Приклад 2. Винести множник із-під знака кореня

Рішення.

Таке перетворення називається винесенням множника з-під знаку кореня. Мета перетворення – спростити підкорене вираження.

Приклад 3. Спростити.

Рішення. За якістю 3° маємо Зазвичай намагаються підкорене вираз спростити, навіщо виносять множники за знак корію. Маємо

Приклад 4. Спростити

Рішення. Перетворимо вираз, внісши множник під знак кореня: За властивістю 4° маємо

Приклад 5. Спростити

Рішення. За властивістю 5° ми маємо право показник кореня та показник ступеня підкореного виразурозділити на те саме натуральне число. Якщо в аналізованому прикладі розділити зазначені показники на 3, то отримаємо .

Приклад 6. Спростити вирази:

Рішення, а) За властивістю 1° отримуємо, що з перемноження коренів однієї й тієї ступеня досить перемножити підкорені висловлювання і з отриманого результату витягти корінь тієї ж ступеня. Значить,

б) Перш за все, ми повинні привести радикали до одного показника. Відповідно до властивості 5° ми можемо показник кореня показник ступеня підкореного виразу помножити на те саме натуральне число. Тому далі маємо в отриманому результаті розділивши показники кореня і ступеня підкореного виразу На 3, отримаємо .

Урок 71. Дробові вирази

Цілі: запровадити поняття дробового виразу, знаменника та чисельника дробового виразу; формувати усні та письмові обчислювальні навички; повторити теорію на тему «Множення та розподіл дробів»; виховувати вміння слухати думку товаришів.

I. Організаційний момент

ІІ. Усна контрольна робота (5 хв)

(На наступному уроці можна змінити варіанти.)

ІІІ. Повідомлення теми уроку

Сьогодні на уроці ми дізнаємося, які вирази називають дрібними. Знаходимо значення таких виразів.

IV. Вивчення нового матеріалу

1. Підготовча робота.

Запишіть у вигляді приватного: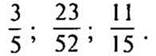

Запишіть у вигляді дробу: 3: 7; 43: 54; 12: 17.

2. Робота над новою темою.

Вираз (2,7 + 5,2): (4,3 - 3,2) можна записати в наступному вигляді: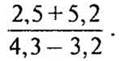

- Знайдіть значення цього виразу. (7.)

Визначення. Частка двох чисел або виразів, у якому знак розподілу позначений рисою, називають дробовим виразом.

Наприклад: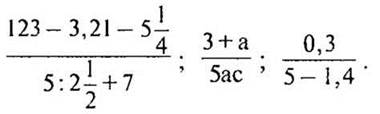

Наведіть приклади дробових виразів. (Запишіть на дошці кілька прикладів.)

Визначення. Вираз, що стоїть над межею, називають чисельником, а вираз, що стоїть під межею, - знаменником дробового виразу.

Назвіть чисельник та знаменник даних виразів.

Зробіть висновок, що може бути чисельником та знаменником дробового виразу. (Будь-які числа, числові та буквені вирази.)

З дробовими виразами можна виконувати самі дії, як і з звичайними дробами.

V. Закріплення вивченого матеріалу

Кожне завдання виконують по три учні біля дошки, інші - у зошитах, самоперевірка.

1. № 693 стор 111. (Відповідь:)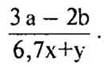

2. № 694 стор. 111.

Згадайте правила множення та розподілу десяткових дробів.

Рішення:

(Всі підрахунки у стовпчик виконуються у зошиті.)

3. № 695 (а, г, ж) стор. 111.

Сформулюйте правило розподілу змішаних чисел.

- Що називають скороченням дробів?

Рішення:

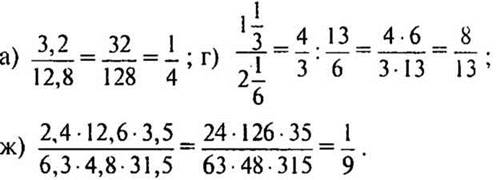
VI. Фізкультхвилинка

VII. Робота над завданням

№ 713 стор. 114 (один учень вирішує на звороті дошки, інші у зошитах, самоперевірка).

Рішення:

1) 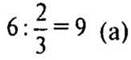- Площу саду.

2) - площа ділянки.

(Відповідь: 21а.)

VIII. Повторення вивченого матеріалу

1. Бліц-опитування з теорії.

Розкажіть, як помножити дріб на натуральне число.

Як виконати множення двох дробів?

Як виконати множення змішаних чисел?

Запишіть властивості нуля та одиниці при множенні.

Сформулюйте правило розподілу дробів.

Як виконується розподіл змішаних чисел?

Сформулюйте правило знаходження дробу від числа.

Сформулюйте правило знаходження числа за даним значенням його дробу.

Які числа називають взаємно оберненими?

2. Тестові завдання (5 хв можна виставити оцінку).

Виконайте тест.

Варіант I

1. У школі 85 учнів взяли участь в олімпіаді, що складає 1/10 учнів. Скільки учнів у школі?

850 – Ь; 750 – Щ; 520 – X.

2. Знайти 40% від 90%.

300 – А; 36 – Р; 360 - До

3. У парку 120 дерев, 5/6 їх берези. Скільки беріз у парку?

15 - М; 18 - Л; 100 – Б.

4. Турист пройшов 50% колії, що становить 16 км. Який шлях туриста?

320 - Р; 8 - У; 32 – Д.

5. У хорі 90 осіб, 1/10 із них – хлопчики. Скільки хлопчиків у хорі?

150 – X; 54-O; 42 - Еге.

Запишіть відповіді в порядку зростання та прочитайте слово.

Відповіді:

Варіант ІІ

1. У ремонті школи взяли участь 94 учні, що складає 1/10 усіх учнів школи. Скільки учнів у школі?

940 – Ч; 360 – Л; 54 – М.

2. Знайти 20% 80.

160 – Ц; 16 - Про; 200 – Ст.

3. У саду 50 дерев, 3/5 яблуні. Скільки яблунь зростають у саду?

100 – Ч; 250 – Д; 30 – С.

4. Пішохід пройшов 8 км, що становить 40% всього шляху. Який шлях пішохода?

30 - Ж; 16 - Е; 20 – Л.

5. У хорі 30 дівчаток, що становить 2/5 всіх учнів у хорі. Скільки всього учнів у хорі?

Як називаються вирази, що знаходяться над межею? Під межею?

Яким може бути чисельник та знаменник дробового виразу?

Домашнє завдання

№ 710, 716 (а, е) стор 114; № 705 стор. 113.